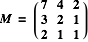MUZZULINI'S article combines a study of historical/philological nature with actual computational research and offers novel results thanks to this very combination. I appreciate its publication in Empirical Musicology Review as I find it fascinating and thought-provoking to interpret the process of theory creation, i.e. the exploratory investigations of a theorist, as an instance of empirical work. The fascination is amplified by the circumstance that the investigation is dedicated to the traces of music-theoretical explorations of none other than Isaac Newton. The overall subject of Newton's notebook entries and – consequently – Muzzulini's study is the search for good approximations of a selection of musical intervals within regular divisions of the octave.
MUSICAL INTERVALS AND THE PITCH HEIGHT OF JUST INTONATION
In this commentary I would like to highlight one particular aspect of music-theoretical and algebraic nature. With the choice of his title Muzzulini tacitly locates genuine musical structures such as the diatonic and chromatic scales and the hexachords within the medium of pitch height. As an alternative to the squeezing of these musical entities directly into a linear pitch height space I would like to advertise a more abstract concept of musical interval space, which supports the investigation of a variety of pitch height interpretations in terms of elements of the associated dual space.
Herein I follow Eric Regener's (1973) approach to the analysis of musical pitch notation as well as Guerino Mazzola's (1990) proposal to model the concept of pitch height in terms of linear forms on an underlying linear interval space. This approach splits the linearity of a single pitch height space into two components: (1) The operation of interval concatenation is modeled in terms of vector addition. This operation is of tremendous musical importance. (2) The mapping of musical intervals into a one-dimensional „medium" of pitch height is accomplished in terms of a linear pitch height form. Its linearity guaratees that interval concatenation is thereby faithfully preserved.
I will argue that this maneuver is more than an ontological sophistry, particularly in connection with Newton's explorations and Muzzini's refinements thereof. To that end I will paraphrase some of their findings along the lines of this approach.
To begin with, we regard three intervals, the perfect octave P8, the perfect fifth P5 and the major third M3 as three linearly independent generators of a 3-dimensional vector space E of musical intervals. The associated limit 5 tuning pitch height can then be given by the linear form h: E -> R with h(P8) = 1, h(P5) = log2(3/2), h(M3) = log2(5/4). Among other possible bases for this musical interval space E we choose Newtons three chromatic step intervals a = P8 - P5 - M3, b = -2 P8 + 3 P5 + M3, c = -P5 + 2 M3 with the transformation matrix:
The columns of this matrix show the chromatic step coordinates of the perfect octave, perfect fifth and major third, respectively. The chromatic basis a, b, c serves as the main reference for the investigation. The transformation M goes hand in hand with its dual map M* which converts pitch height forms, given in chromatic coordinates into their associated octave-fifth-third coordinates. Hence, the inverse dual map (M*)-1 sends the co-vector u = (1, log2(3/2), log2(5/4)) to its associated representation in chromatic coordinates v = (h(a), h(b), h(c)) = (log2(16/15), log2(135/128), log2(25/24)).
MODIFYING THE PITCH HEIGHT FORM
Looking through the lens of this approach, we will see that central findings in Newton's and Muzzulini's explorations are closely related to modifications of this co-vector v: for every natural number n > 0 we obtain a linear form hn by replacing the coordinates of the augmented co-vector n.v by the nearest integer-coordinates, respectively. More explicitly, if r[x] denotes the integer closest to a real number x, then hn is represented by the co-vector vn = (r[n log2(16/15)], r[n log2(135/128)], r[n log2(25/24)]).
The empirical question behind this definition is how one can measure the musical suitability of such a modified linear form hn as an alternative pitch height interpretation of the interval space E. And the answer should grasp relevant apects of Daniel Muzzulini's evaluation of chromatic n-EDO scales, which he explicates in terms of (in)consistency-levels and a "log-compatibility"-criterion.
The following definition draws upon a set C of musical intervals chosen a priori. It is meant to represent the core of the musical interval system: The pitch height form hn is said to be consistent with respect to the interval set C, if the equation hn(i) = r[n.h(i)] is satisfied for all intervals i in C. This consistency condition means that the values hn(i) under the modified linear form should coincide with the isolated roundings of their original pitch heights, when augmented by the factor n.
If we choose C = {7a+3b+2c} to be just the singleton set containing the octave, the definition is satisfied for all those hn which satisfy hn(7a+3b+2c) = n. Comparing this with Muzzulini's terms we may state — for the time being —, that this matches the condition to be "consistent and log-compatible with respect to the three chromatic intervals a, b, c". Between n = 1 and n = 5000 there are 711 linear forms, which are consistent in this sense. 2
The core collection of musically prominent notes from Newton's notebook is the chromatic scale G – Aflat – A – Bflat – B – C – Csharp – D – Eflat – E – F – Fsharp – G' with the step interval pattern (a, b, a, c, a, b, a, a, c, a, b, a). Translating the scale notes to intervals anchored in the first note G, we would consider in the role of the core set C the vector sums of the twelve prefixes of this chromatic step interval pattern, i.e., the intervals a = (1, 0, 0), a+b = (1, 1, 0), 2a+b = (2, 1, 0), 2a+b+c = (2, 1, 1), etc. till 7a+3b+2c = (7, 3, 2). In this case the definition matches Muzzulini's "log-compatibility" criterion for the entire scale. Experimentally, I found to my surprise that all the 14,275 octave-consistent instances among the linear forms hn (n < 100000) turn out to be consistent with respect to these 12 chromatic intervals as well. Does plain octave consistency imply scale consistency for Newton's scale? This would be an interesting property of this scale, because for random permutations of the pattern this does not hold anymore.
As a musically reasonable strengthening one may consider the vector sums of all factors of the cyclically conceived chromatic step interval pattern in the role of the core set C. In this case the equation hn(i) = r[n.h(i)] should be satisfied for all internal intervals of Newton's chromatic scale. Among the 711 consistent linear forms I found 421 satisfying this stronger condition. 3
INSPECTING THE MUZZULINI TRANSFORM
In his advanced continuation of Newton's investigation Muzzulini offers an elegant method for the control of the variety of consistent and "log-compatible" chromatic n-EDO scales. After the familiar 12-equal-tempered chromatic scale he identifies the three cases n = 53, 118 and 612 as the best approximations of Newton's chromatic scale with respect to the measurement of the deviation from just intonation, each of them better than the previous ones. What he then does with these three extraordinary cases, can be rephrased as follows:
The three chromatic delta functions a*, b* and c* with a*(a) = 1, a*(b) = a*(c) = 0, b*(b) = 1, b*(a) = b*(c) = 0, c*(c) = 1, c*(a) = c*(a) = 0 constitute a basis in E*, dual to the basis {a, b, c} in E. The three linear forms h612, h118 and h53 form another basis of the dual space E*: the Muzzulini basis. The columns of the unimodular transformation matrix T* show the chromatic coordinates of the linear forms h612, h118 and h53, respectively. Analogously, the columns of the inverse matrix T*-1show the Muzzulini-coordinates of the chromatic delta functions ha, hb, hc.
The rows of the matrix T*-1 (i.e., the columns of the transposed matrix T*-1* = T-1) also represent the chromatic coordinates of the dual Muzzulini basis. And we get a nice explication of an observation in the article, namely that Newton's pitch height form h612 is dual to the interval -a+2b-c, whose pitch height is also known as the schisma. It is the difference h(-a + 2b - c) between the Pythagorean comma h(-a + 3 b - 2 c) and the syntonic comma h(b - c) and, likewise, it is the difference between the syntonic comma h(b - c) and the diaschisma h(a-b). In old-fashioned frequency ratios this can be written as 32,805/32,768 = (531,441/524,288)/(81/80) = (81/80)/(2,048/2,025). The other two intervals of this basis need getting used to: -4a-3b+5c maps to the micro-chromatic step interval in 53-EDO, but vanishes in 118-EDO and 612-EDO, while 7a-9b+3c maps to the micro-chromatic step interval in 118-EDO, but vanishes in 53-EDO and 612-EDO. The behavior of the latter two intervals thus illustrates interesting side effects of the rounding procedure.
Figure 1 displays the 5,000 linear forms h1, … h5000, and illustrates the location of the 711 consistent ones among them as well as the 241 linear forms which are consistent with respect to the internal intervals of Newton's chromatic scale. They are shown as points in Muzzulini coordinates within a cuboid. One can think of these points as vectors in E (acting on E via scalar product). The convex closure of each of the three point clouds is shown to illustrate the effectivity of this basis. We note though, that these convex closures contain other integral points as well.
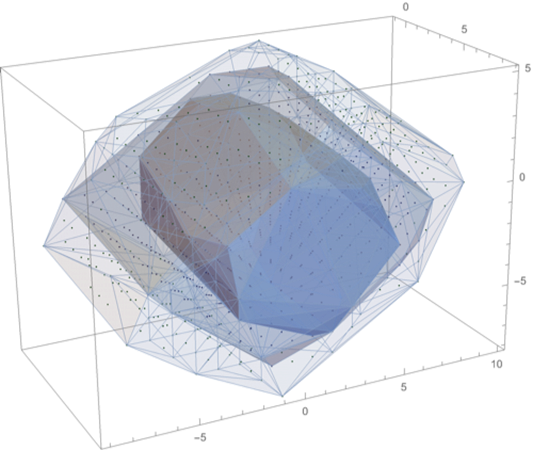
Figure 1: Outer Shape (light gray): Representation of the linear forms hn (n = 1, …, 5,000) as points in Muzzulini coordinates. Middle Shape (medium gray): Representation of the 711 consistent linear forms among these. Inner Shape (dark gray): Representation of the linear forms which are consistent with all internal intervals of Newton's chromatic scale.
Thus, we see that the height forms hn up to some limit (such as n = 5,000) are nicely clustered within a bounded region in E*. Those which are octave-consistent, are concentrated in a smaller subregion, and those which are furthermore consistent with all the chromatic intervals occupy a still smaller subregion of the former. In order to explain the effect of the transformation T* (turning Muzzulini coordinates into chromatic coordinates) geometrically, it is useful to inspect its eigen co-vectors. T* is a Pisot transformation with the large real eigenvalue 69.2025 and the corresponding normalized eigen-co-vector (0.6943, 0.5711, 0.4379). This eigen-co-vector is quite close to the normalized coordinate representation (0.6933, 0.5719, 0.4385) of the pitch height form h. As a consequence of this property, the transformation maps small ball-like point clouds into elongated tube-like point clouds along this eigen-direction, which almost coincides with the pitch height direction.
PONDERING ABOUT NEWTON'S CHROMATIC MODE
Apart from the issue of n-EDO approximations, the publication of Muzzulini's article in EMR is thought-provoking in view of the open empirical status of Newton's chromatic scale itself in terms of musical relevance, be it with respect to the music of the 17th century or beyond. To some extent was Newton indeed committed to this particular step interval pattern (a, b, a, c, a, b, a, a, c, a, b, a). After all, with respect to the search for embeddings in suitable n-EDOs he was in the first instance interested in the representation of the pattern and only in the second instance in good numerical approximation. In figure 9b of the article Muzzulini reproduces a table with n-EDO representations, where one row sticks out: The sequence (0, 4, 2, 6, 1, 5, 3, 7, 11, 6, 10, 8, 12) is not monotonously growing like the pitches of a scale. Butwhatever the numbers meant for Newton, they still exemplify the pattern with 4 representing a, -2 representing b and -5 representing c.
The question is: shall such 12-letter patterns (like Mercator's, Newton's, Holder's or Euler's) be investigated as chromatic refinements of the diatonic modes? What are the conditions of fulfillment for an affirmative answer? Over the centuries music theorists have paid considerable attention to the classification of the step interval patterns of the diatonic modes. And since the new-era theorists have also studied tone repertories, intervals and chords in the three-dimensional space, generated by intervals of the major and minor triads. But chromatic modes do not seem to have gained a strong interest so far. Does this mean that there exists a broad consensus that their study is irrelevant? Or is it a potentially interesting unexplored territory? Which kind of research questions would have to be raised?
In music cognition and in music theory there is a renewed interest in the study scale degree qualia. This concept attributes different qualities to the diatonic scale degrees apart from their pitch height. Guido explained the different characters of the notes of a mode (propriatas sonorum) in terms of their different step interval neighborhoods. Would it make sense to extend this concept to a level of chromatic modes?
The theoretical path from the concept of (pseudo-classical) mode to Newton's chromatic "mode" combines two different kinds of refinement, namely: (1) the chromatic extension of a diatonic mode on the level of notes as such as (a+b, a+b, a, b+a, a+b, a+b, a), and (2) the refinement (for example) of the authentic Ionian mode T-T-S-T | T-T-S through Zarlino's syntonic-diatonic mode T-t-S-T | t-T-S. Newton's pattern accounts for a combination of both procedures. But the "refinement" also entails obstructions for a seamless extension of the diatonic theory. Guido's affinities of the hexachord T-T-S-T-T (its double periodicity with respect to the prefixes T-T-S-T and T-T-S) does not hold anymore for Descartes' and Newton's syntonic hexachords t-T-S-T-t and T-t-S-T-t. Nonetheless, it could be worthwhile to explore the potential meanings of chromatic scale degree qualia.
At present there are two different approaches available. Huron (2006) sees the different profiles of transition probabilities from a given scale degree to the others as a clue for statistical learning and interprets scale degree qualia as a side effect of statistical cognition. In Noll (2018a, 2018b) I constructed exo-modes, i.e., parametrizations of different musical qualities of one the same interval or interval combination. Geometrically, these exo-modes are located in the kernel (the zero-space) of a suitably chosen pitch height form. Noll (2018a) is dedicated to diatonic and chromatic exo-modes in Reger's (1973) two-dimensional note interval space, while Noll (2018b) is dedicated to the study of the exo-partners of Zarlino's syntonic-diatonic modes in the three-dimensional interval space E. As far as I see, nothing should be in the way of applying the approach taken in Noll (2018b) to Newton's chromatic mode.
This perspective of achieving a parametrization of possible tone qualia in the orthogonal complements of the gradients of pitch height forms adds to my motivation to object against the squeezing of musical scales and related entities into the one-dimensional pitch height space.
ACKNOWLEDGEMENTS
This article was copyedited by Matthew Moore and layout edited by Diana Kayser.
NOTES
-
thomas.mamuth@gmail.com
Return to Text -
The sequence starts with 12, 19, 22, 31, 34, 41, 43, 46, 53, 65, 75, 77, 84, 87, 96, 99, 106, 111, 118, 130, 140, 149, 152, 159, 164, 171, 183, 193, 205, 212, 214, 217, 224, 236, 246, 248, 258, 270, 277, 280, 282, 289, 301, 311, 323, 330, 335, 342, 345, 354, 364, 366, 376, 388, 395, 398, 400, 407, 419, 429, 441, 448, 453, 460, 463, 472, 482, 484, 494, 506, 513, 516, 518, 525, 528, 537, 547, 559, 566, 571, 578, 581, 590, 593, 600, 612, …
Return to Text -
The sequence starts with 12, 34, 41, 53, 65, 87, 106, 118, 130, 140, 152, 159, 171, 183, 193, 205, 217, 224, 236, 248, 258, 270, 277, 289, 301, 311, 323, 335, 342, 354, 376, 388, 407, 419, 429, 441, 453, 460, 472, 482, 494, 506, 525, 537, 547, 559, 571, 600, 612, …
Return to Text
REFERENCES
- Huron, D. (2006). Sweet Anticipation. Music and the Psychology of Expectation. Cambridge, MA: MIT Press. https://doi.org/10.7551/mitpress/6575.001.0001
- Mazzola, G. (1990). Die Geometrie der Töne. Birkhäuser. Basel. https://doi.org/10.1007/978-3-0348-7427-4
- Noll, T. (2018a). One Note Samba: Navigating Notes and their Meanings within Modes and Exo-Modes. In M. Montiel & R. Peck (Eds.), Mathematical Music Theory: Algebraic, Geometric, Combinatorial, Topological and Applied Approaches to Understanding Musical Phenomena. https://doi.org/10.1142/9789813235311_0006
- Noll, T. (2018b). Dual lattice-path transformations and the dynamics of the major and minor exo-modes. Journal of Mathematics and Music 12 (3), 212-232. https://doi.org/10.1080/17459737.2018.1548035
- Regener, E. (1973). Pitch Notation and Equal Temperament: A Formal Study. University of California Press, Berkeley.