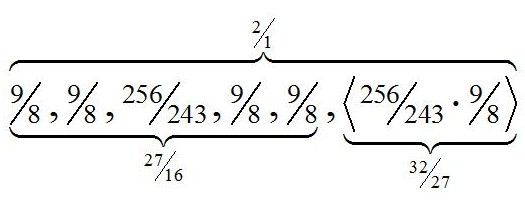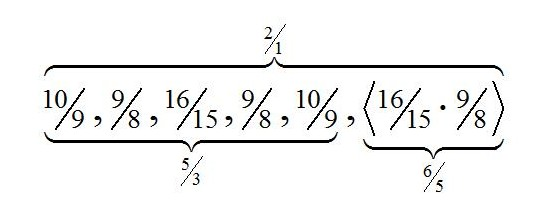ISAAC Newton (1643-1727) is known for his outstanding contributions to mathematics and physics. In the 1660s he invented the mirror telescope and developed the basics of the theory of ray optics published in Opticks (1704). His early contributions to music theory are less known and were not published during his lifetime. A college notebook from 1665 contains the draft of a music theoretical treatise, which has been recently edited critically by Benjamin Wardhaugh 2. Newton's manuscript contains two circular diagrams which are inspired by Descartes's Compendium Musicae (1650). Newton's diagrams interpret and generalize Descartes's just intonation hexachordal system through octave divisions into 53 and into 120 equal parts, see Figure 2. The idea to approach just intonation through 53-EDO 3 was brought about by Nicolaus Mercator at about the same time – also in manuscripts, see Wardhaugh (2013, pp. 129-236). Due to an early quotation by William Holder (1694/1730, pp. 79-80) Mercator's treatment of the tuning problem is better known than Newton's note book. Besides the mentioned divisions Newton considered several other equal division of the octave (EDOs) with respect to their capacity to approximate just intonation tunings. These EDOs are in the focus of this article.
After a brief introduction into Pythagorean and just intonation tunings, I will give some remarks on the construction of syntonic chromatic scales in historical sources. The following close reading of Newton's sketchy note book tries to clarify why he studied certain octave divisions and neglected others.
In order to tackle Newton's optimization problem with modern means, I calculated the closest approximation to Newton's syntonic chromatic scale for all equal divisions of the octave with up to 5000 microtonal steps per octave and analysed them in terms of least square deviations and consistency. This analysis helps to assess Newton's selection of octave divisions systematically and it leads us to a general approach to the tuning problem and to an elegant description of the dependence of the best fits from the fineness of the approximating scales, i.e., their number of equal steps per octave.
The use of least square deviations to assess the quality of best fit approximation problems is a mathematical standard with many applications in data analysis, especially in statistics and probability theory. In the 19th century it was applied to musical scales by Drobisch (1852, pp. 75-78) and more recently by James M. Barbour (1951) and Johannes Barkowsky (2007, p. 105). Barbour's approach, which takes 12-EDO as a reference scale to assess chromatic and enharmonic scales, was criticized by Donald Hall (1973).
The approximation problem studied in this article is not of a genuinely stochastic nature, because the content of the datasets generated by computer programs are uniquely determined. Nevertheless, they appear to the eye as a kind of random data. The knowledge of three excellent n-EDO representations of the syntonic chromatic scale, 53-EDO, 118-EDO and 612-EDO, explains the quasi-chaotic dependence of the quality of best fit on n for values of n up to 1200 very well. In other words, for EDOs with unit steps not smaller than 1 cent, the discrete interval configuration of the just intonation scale and the approximating space are both three-dimensional. 4 Newton had accurate tables of (base 10) logarithms at his disposal and he used them to measure just intonation intervals with 12-EDO semitones, but he had no powerful computers and software. The "empirical" approach to Newton's approximation problem given here is in line with his selection of octave divisions and it reveals general properties of equal octave division and their capacity to simulate just intonation tuning by combining them linearly.
JUST INTONATION: LIMIT-3 AND LIMIT-5 TUNING
Pythagorean music theory is based on the idea that musical intervals can be described with ratios of small positive integers. In antiquity these ratios refer to string lengths on a monochord. 5 The diatonic genus and the related pitch systems of the Pythagoreans, as passed down to the Middle Ages and the Renaissance, can be defined by ratios of numbers which have only 2 and 3 in their prime number factorisations. In modern terminology and notation, the so-called "Pythagorean tuning" 6 is given by rational numbers of the format 2k ⋅ 3j where k and j are integers (positive, zero or negative). The set of numbers L3:= {2k ⋅ 3j |k,j ∈ } is a dense subset of the real numbers, which hereafter is called limit-3 tuning (system). Finite subsets of L3 can be used to define the Pythagorean intervals, chords and scales.
Historical sources often describe pitch sets with multi-terms proportions of integers and visualize them on monochord drawings. In order to describe an octave periodic scale or chord, the first and last element of the related proportion are of the ratio 2 : 1. The Pythagorean proportion
6 : 8 : 9 : 12 = (21 ⋅ 31) : (23 ⋅ 30) : (20 ⋅ 32) : (22 ⋅ 31),
for example, serves as a reference frame for the Greek diatonic, chromatic and enharmonic genera. Pitch systems from the late Renaissance and later periods are usually strictly octave periodic. However, this is not necessarily the case in the Middle Ages and antiquity. 7
Syntonic tunings or limit-5 tunings are defined in the same way with the sole prime factors 2, 3 and 5, and limit-7 tunings with the prime factors 2, 3, 5 and 7:
L5:= {2k ⋅ 3j ⋅ 5i |k,j,i ∈ }, L7:= {2k ⋅ 3j ⋅ 5i ⋅ 7h |k,j,i,h ∈ }
Limit-5 tunings can be constructed by combining octaves (2 : 1), Pythagorean fifths (3 : 2) and (just) major thirds (5 : 4). 8 Limit-7 tunings also permit "just minor sevenths" (7 : 4), but normally without piling them, so that the value of the power index h in the formula for L7 equals -1, 0 or 1. Limit-7 tunings were suggested by several theorists from the 17th to the 20th century, among them Christiaan Huygens (c. 1661) and Quirinius van Blankenburg (1739), see Jedrzejewski (2018). Musicians referring to "just intonation" usually mean limit-5, but sometimes also limit-7 tuning. In this text we frequently use the term "syntonic scales" for subsets of L5. 9
Octaves, Pythagorean fifths and just major thirds are base vectors of a three dimensional "interval space" 3 = {(k,j,i)|k,j,i ∈ } defined by the power indices from L5. Because of the uniqueness of the prime factorization there is a natural embedding:
3 = {(k,j,i)|k,j,i ∈ } ≅ L5 ⊂ ⊂
Hereby, different points in 3 correspond to different frequency ratios and arbitrary irrational numbers can be approximated arbitrarily well through limit-5 ratios, which means that L5 is a dense subset of the real numbers .
Nicolas Mercator in the 17th century was probably the first to represent limit-5 tunings with two-dimensional grids which abstract from the octave coordinate 10. Jean-Philippe Rameau (1726), Leonhard Euler (1739) and others in the 18th century used the same technique to visualize scales and chords on a two-dimensional lattice. The number triangles used by Boethius, Torkesey and their followers up to Robert Fludd in the early 17th century are precursors of two-dimensional pitch grids; however, they do not abstract from octave similarity. 11 Isaac Newton did not use grid notation in order to describe just intonation tunings, which possibly means that he did not know Mercator's manuscripts when he studied EDOs. Newton favoured combinatorics and circular arrangements which he picked up from Descartes' Compendium Musicae, see Figures 1b and 2a.

Figure 1a. Mercator's two-dimensional representation of the syntonic diatonic scale, together with the corresponding numbers composed of prime powers of 3 and 5 below the horizontal line - neglecting the octave information (Mercator, MS MUS. 1187 fol. 11v, by permission of the Christ Church Library, London)

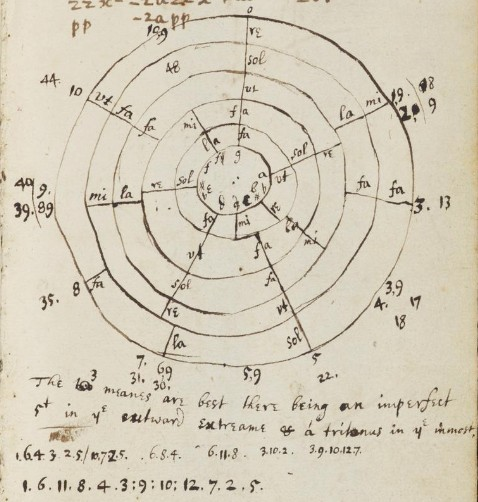
Figure 1b. Newton describes syntonic scales through three kinds of semitones, the diatonic semitone a, the greater chromatic semitone b and the lesser chromatic semitone c, which he arranges on an octave circle (Newton 1665, fol. 110r).
Incommensurable intervals: Euclid's algorithm and continued fractions
The mathematical reason for the quasi-chaotic appearance of the datasets discussed below is the mutual incommensurability of the logarithms of the primes 2, 3 and 5 (expressed in any common base, conveniently 2). This incommensurability can be summarized with the following three formulas:
- (i) log2(3) ∈ \
- (ii) log2(5) ∈ \
- (iii) log2(5) / log2(3) ∈ \
Being irrational numbers, these expressions cannot be written as integer ratios (ordinary positive fractions). Translated into music theory the first formula (i) is equivalent to the incommensurability of the just fifth and the octave so that chains of Pythagorean fifths modulo octave generate scales with potentially infinitely many pitches per octave. The second formula (ii) means that major thirds of the ratio 5 : 4 are incommensurable to the octave in the same sense. And the third formula (iii) states that just major thirds and fifths are also mutually incommensurable in terms of musical interval size. The fact that intervals of superparticular ratios are mutually incommensurable has been known since antiquity.
Historically, commensurability was tested with Euclid's algorithm, which provides a method to distinguish rational from irrational ratios of quantities: Euclid's algorithm terminates after finitely many iteration steps, if and only if the ratio of the quantities under consideration is rational. The Pythagoreans knew this fact and that the algorithm does not terminate if it is applied to the diagonal and the side of a regular pentagon. In other words, they proved that the so-called golden ratio is irrational 12. The application of Euclid's algorithm onto pairs of musical intervals viewed as continuous quantities (like distances on a straight line) produces their continued fraction expansion as a by-product. If this expansion is finite, the intervals under consideration are commensurable, otherwise they are incommensurable. In the Sectio canonis, assigned to Euclid, it is shown that any different intervals with superparticular frequency ratios (integer ratios of the form ) are mutually incommensurable. Boethius knew this result and discussed a proof by Archytas 13. Whereas the continued fraction expansion of the golden ratio,, is periodic with the simplest possible pattern [1, 1, 1, 1, …], the interval ratios related for pairs of superparticular frequency ratios have infinite continued fractions expansions which do not exhibit simple regular patterns. 14
NEWTON'S CHROMATIC SCALES AND HIS VARIOUS OCTAVE DIVISIONS
Descartes's adaption of the hexachord system to just intonation and its reduction to octave classes, as well as Newton's extension of Descartes's approach, lead us to the problem of defining just-tuned diatonic and chromatic 12-note scales. Differently from the Pythagorean scales of the Middle Age, which offer only few alternatives, there was no consensus about the definition of a chromatic scale in just intonation in the 17th and 18th centuries. Various chromatic scales were proposed, which occupy different and incongruent regions in pitch grids for just intonation. 15.
From syntonic hexachords to chromatic scales
Guido of Arezzo's Micrologus (c. 1025) constructs a tone system with seven overlapping hexachords "ut-re-mi-fa-so-la", each of them of the same symmetric interval structure T-T-s-T-T, a Pythagorean diatonic semitone s (256 : 243) flanked on both sides by pairs of major tones T (9 : 8). Guido of Arezzo placed these congruent hexachords at ut = Γ, C, F, G, c, f and g, so that his system comprises two octaves plus a major sixth [Γ, ee], where Γ, the lowest note of the system, is one octave below G, and ee, the highest note of the system one octave above e. There is no B-flat in the lowest octave, but B-flat and B in the middle and upper octaves.
The Pythagorean hexachord (PythHex) can be completed to octachords (PythOct), so that the octave is portioned into five tones and two diatonic semitones, see Table 1. For this purpose, the minor third (32 : 27) between the major sixth (27 : 16) and the octave, is divided into a Pythagorean semitone and a major tone, which results in two equivalent diatonic scales a Pythagorean fifth/fourth apart. Hence, the Pythagorean hexachord PythHex on C together with the transpositions by a fourth (4 : 3) and by a fifth (3 : 2) generate a limit-3 diatonic system of eight pitch classes, C-D-E-F-G-A-B♭-B, if the pitches are reduced to one octave. The pitches can be arranged as a stack of fourths B-E-A-D-G-C-F-B♭ with the chromatic semitone B♭-B of the ratio 2187 : 2048, which is approximately 25% larger than the diatonic semitones E-F and B♭-B of the ratio 256 : 243.
| Pythagorean hexachord | Pythagorean octachords | |
|---|---|---|
| Interval structure | T-T-s-T-T | T-T-s-T-T-s-T T-T-s-T-T-T-s |
| Ratio structure |
Note: The two octachords are cyclic permutations of the same interval pattern. They define the same diatonic scale.
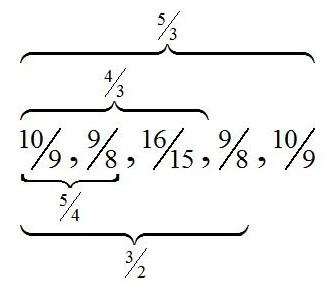
Guido's system was quoted time and again through the late Middle Ages and Renaissance up to the Templum musicae (1618/24) by Robert Fludd (1618/24, p. 161) published immediately before René Descartes (1596-1650) composed the Compendium musicae dedicated to Isaac Beeckman (1619). The Compendium written 1618, the earliest complete treatise by Descartes, circulated in at least four manuscript copies during his lifetime, only 1650 immediately after his death it appeared in two Latin prints and three years later afterwards in an English edition (1653). Descartes's manuscript is lost. 16 One of the four circular pitch diagrams contained in the Compendium Descartes gives a system of three structurally identical hexachords "ut-re-mi-fa-so-la" (mollis, naturalis and duris), whose references are Pythagorean fifths apart as in Guido's system, but whose symmetric interval configuration t-T-S-T-t is composed of superparticular limit-5 ratios with major tones T (9 : 8), minor tones t (10 : 9) and diatonic semitones S (16 : 15) in place of Guido's limit-3 intervals. Descartes's syntonic hexachord and its completions to octachords are shown in Table 2.
| Symmetric syntonic hexachord | Syntonic octachords | |
|---|---|---|
| Interval structure | t-T-S-T-t | t-T-S-T-t-S-T t-T-S-T-t-T-S |
| Ratio structure |
Note: The two ways of dividing the minor third between the sixth scale degree and the octave lead to two incongruent diatonic scales, in which the order of the major and minor tones between the respective tonics and their third scale degrees are reversed. Newton looked at both types of diatonic extensions, see Figures 2c/d.
Descartes' re-interpretation of Guido of Arezzo's Pythagorean hexachords results in a diatonic just intonation system with both varieties of B (B-duris and B-mollis) and two ambiguous pitches D and G, see Figure 1a. Just intonation as well as meantone temperaments were investigated and widely debated in the 16th century by Fogliano (1529), Gioseffo Zarlino (1558/62, 1588), Francisco Salinas (1577) and Vincenzo Galilei (1581). Just intonation was usually justified by the consonance of the major thirds and by referring to Ptolemy's superparticular tetrachord divisions.
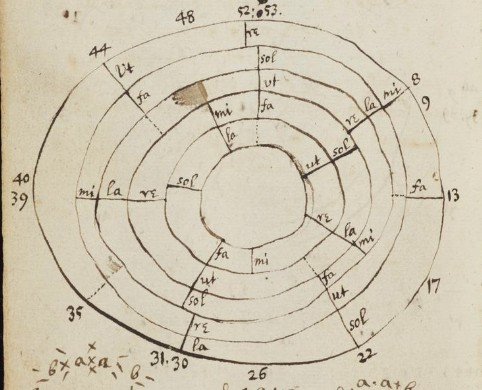
The use of concentric rings to visualize hexachordal tone systems has a very early forerunner in Theinred of Dover (Ms. Bodley 842, mid-twelfth or early fourteenth century), where four hexachords are represented on a circle that closes after two octaves, see Figure 2b 17 Theinred's visualization was probably not known to Descartes, and almost certainly not to Newton. Descartes, however, was at least superficially familiar with Zarlino's theories from his college education at Flèche 18. Zarlino's Sopplimenti musicali contain a diagram, which could have been a source of inspiration for one of Descartes's circular pitch diagrams, Zarlino (1588, Libro Ottavo p. 296). Newton in 1665 certainly knew either the English or more likely the Latin edition of Descartes's Compendium musicae, when he investigated musical scales.
Newton's constructions shown in Figures 2c and 2d hold five seven-note scales (ut-re-mi-fa-sol-la-fa) instead of the three Cartesian hexachords (ut-re-mi-fa-sol-la) with ut = F-C-G-D-A and four ambiguous notes D, A, E and B. The hexachords of Figure 2c are equal to Descartes's (t-T-S-T-t) whereas in Figure 2d they are of the format T-t-S-T-t with a major tone T between ut and re. The numbers around the circle refer to 53-EDO and in Figure 2d also to 120-EDO (semitones to 1 d.p.). The seventh grades fa, the minor sevenths with respect to ut, are indicated but not labeled in Figure 2c. Together Newton's five seven-note scales cover eleven out of twelve chromatic pitches (without G♯/A♭).
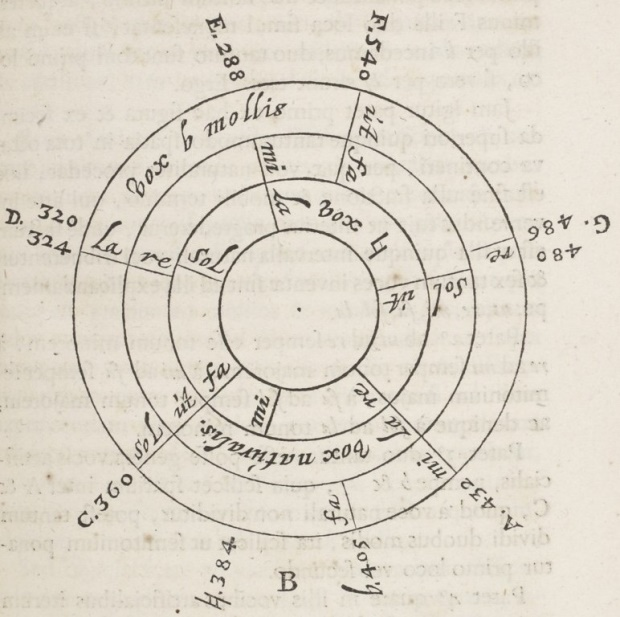
Figure 2a. Descartes' just intonation hexachords (ut-re-mi-fa-sol-la) with ut = F, C and G result in two ambiguous notes, G and D, differing by syntonic commas (324 : 320= 80 : 81 = 486 : 480). (Descartes 1650, 35)

Figure 2b. Theinred of Dover's hexachords on a two-octave circle with four hexachords on ut = B♭, F, C, G together with an interpretation in terms of a 12 semitone note frame without F♯. The tuning is not specified, so that the diagram is compatible with Pythagorean as well as 12-EDO tuning, depending on the interpretation of the Tonus and Semitonium. (MS. Bodley 842, fol. 80v)
Figures 2c/2d. Newton's generalization of Descartes's hexachords (Newton 1665, fol. 110r, fol. 109r, MS Add. 4000: Reproduced by kind permission of the Syndics of Cambridge University Library).
Syntonic chromatic scales with 12 pitches per octave
In his college notebook, Newton expressed the sizes of the syntonic intervals by 12-tempered semitones with an accuracy of 0.0001 cent (see Figure 8) 19. There are various ways to select the pitches of a 12-note chromatic scale within L5. The pitch sets from the Figures 2c and 2d are inconsistent with Figures 3 and 8, because the transpositions of the syntonic hexachord/scale by multiples of Pythagorean fifths generate configurations which are contained in two rows of fifths instead of three rows as in Figure 3.
Whereas Pythagorean chromatic scales have only two kinds of semitones, syntonic chromatic scales are composed of three or four differently sized semitones (see Figures 4 and 5). Newton's chromatic scale is equivalent to a scale proposed by Marin Mersenne (1636), and it has three kinds of semitones: seven diatonic semitones a of the ratio 16 : 15, three greater chromatic semitones b of the ratio 135 : 128 and two lesser chromatic semitones c of the ratio 25 : 24, producing the semitone pattern "a-b-a-c-a-b-a-a-c-a-b-a" with reference G, see Figures 3a/3b. It also contains a Pythagorean third F-A (81 : 64) defined through four Pythagorean fifths 20 so that the major triad F-A-C has a "mistuned" third compared with the perfect major triads on C, G and D of the G major scale. Holder's scale has five lesser chromatic semitones (25 : 24) but no greater chromatic semitones. Whereas the scales by Newton and Holder have only three different semitones, the solutions by Mercator and Euler require all four different semitones shown in Fig. 4. Euler's selection is equivalent to a configuration proposed by Athanasius Kircher (1650), and Newton's selection to a configuration by Marin Mersenne (1636). The earliest syntonic scale over three generations of fifths with precisely 12 pitch classes is by Kepler (1619). 21
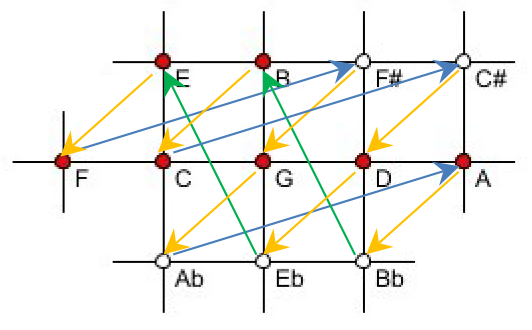
Figure 3a. Newton's syntonic chromatic scale in a rectangular pitch grid as a closed vector path. The notes (pitch classes) of the C-major scale are highlighted. The G-major scale is congruent with the standard diatonic major scale as described by Mercator, see Figure 1a.

Figure 3b. The three kinds of semitones, a, b and c, of Newton's chromatic scale together with their frequency ratios. The vector b + a forms a major tone of the ratio 9 : 8, and c + a forms a minor tone of the ratio 10 : 9, see also Figure 1b.

Figure 4. Vector representations of the four kinds of semitones occurring in limit-5 tunings. The lesser and greater chromatic semitones, as well as the ordinary and large diatonic semitones, differ by syntonic commas; the lesser chromatic and ordinary diatonic semitones, as well as the greater chromatic and large diatonic semitones, differ by enharmonic changes or major diesis (128 : 125) – an octave minus three just major thirds.
612-EDO
In his notebook, Newton examined the divisions of the octave into 15, 19, 20, 24, 25, 29, 36, 41, 51, 53, 59, 100, 120 and 612 equal parts in order to approximate the syntonic chromatic scale, see Figures 9a to 9d. How did he arrive at this particular selection of octave divisions, and how accurate are they? The most striking number is certainly 612, which results in a microtonal unit of little less than 2 cent. If a sound of 440 Hz 22 is increased by this tiny interval, its frequency increases by 0.5 Hz only. The algebraic key to this specific division of the octave can be found in Figure 6a.

Figure 6a. The curves in the central part analyze all the intervals of the chromatic scale, whether they are greater or smaller than the corresponding intervals with respect to G. Newton (1665, 108r) 23.
The "numbers" in Figure 6a/6b indicate sizes of the syntonic intervals with respect to G in terms of 12-EDO semitones plus/minus unit fractions of 12-EDO whole tones. The fractions not highlighted red or blue in the transcription permit the calculation of the 612-EDO representation of the pitch set G-A♭-A-C-D-F-F♯-G containing optimum approximations of the Pythagorean sequence F-C-G-D-A as well as perfect minor and major triads F-A♭-C and D-F♯-A (spanning three rows of fifths), so that the overall quality of the approximation within the region of Newton's scale is made sure. Comparing the factorizations of the neighbored numbers 612, 615 and 611 with the denominators in Figure 6b (612 = 12 · 51 = 36 · 17 , 615 = 41 · 15 and 611 = 47 · 13) helps to understand why Newton preferred 612-EDO having a Pythagorean comma equivalent of 12 units, see also Appendix_1 (http://hdl.handle.net/1811/92832). The three groups of pitches defined by the denominators in Figure 6b are highlighted in Figure 7 with the same colors. The denominators are symmetrically arranged about the tritonus/diminished fifth in the middle between C and D. The denominator 41 makes Newton's scale slightly asymmetrical. The number 6 instead of 6 - would have meant perfect symmetry, but tritonus and diminished fifth cannot be equal in just intonation. 24 Making Newton's chromatic scale mirror symmetric in limit-5 tuning would require two different pitches C♯ and D♭ (6 ± ), i.e., 13 pitches per octave. Newton addresses this point by giving two opposite scales in Figure 6a.
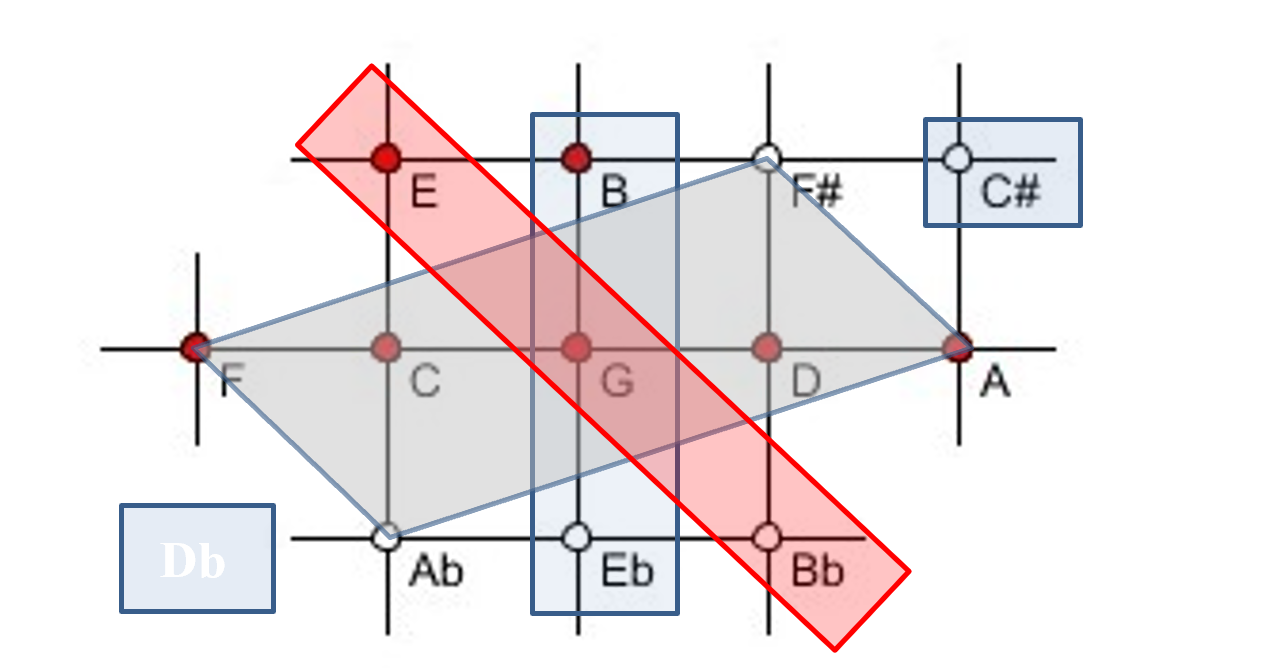
Figure 7. The 612-EDO pitches of the notes described in Figures 6a/b correspond to pitches on and within the parallelogram F-A♭-A-F♯. The pitches D♭, E♭, G, B, C♯ fit to 615-EDO.
The intervals of Newton's chromatic scale in 612-EDO are shown in Table 3. Among the equal divisions of the octave looked at by Newton the division into 612 parts provides the most accurate approximation of the chromatic scale, not primarily because 612-EDO has the largest number of parts, but because the deviations of the best fit measured in unit intervals are the smallest. For example, 720-EDO is less accurate than 612-EDO, although it has a smaller unit interval 25.
| G | A♭ | A | B♭ | B | C | C♯ | D | E♭ | E | F | F♯ | G |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 57 | 104 | 161 | 197 | 254 | 301 | 358 | 415 | 451 | 508 | 555 | 612 |
| 0 | 56.983 | 103.994 | 160.977 | 197.020 | 254.003 | 301.014 | 357.997 | 414.980 | 451.023 | 508.006 | 555.017 | 612 |
Note: The deviations to the decimal values (3 d.p.) in the last row, as calculated with logarithms, have a maximum of only 0.023 for B♭ and E.
Since Newton measured the deviations in unit fractions of 6-EDO units (whole tones) the denominators of the obtained rationalizations are necessarily multiples of 6. Newton searched for good approximations with fewer parts than 612, and he probably wanted to make them independent of the 12 equally spaced semitones, which he used to measure the syntonic chromatic scale. He could achieve this by examining equal divisions of the octave with unit intervals which are multiples of the unit of 612-EDO like 306-EDO, 204-EDO or 51-EDO determined by the divisors of 612. The 51-EDO unit is in the range of the pitch resolution of the human ear for pairs of successive tones and about the size of the Pythagorean comma. Newton's numbers for the chromatic scale in 51-EDO are on top of his list, shown in Figure 9b.

Figure 8. Newton gives base 10 logarithms of the intervals of the syntonic chromatic scale (3rd column). The last number column expresses these intervals as multiples of 12-tempered semitones with an accuracy of 0.0001 cent. Newton (1665, 105v)
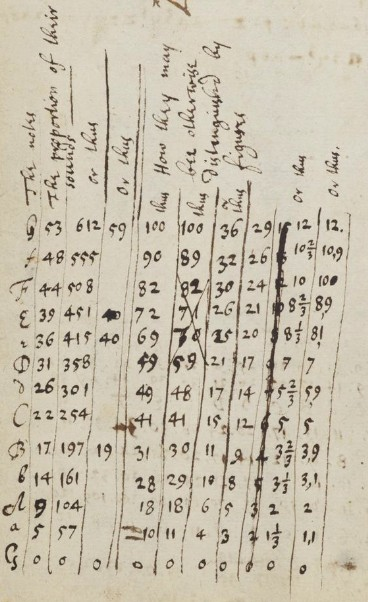
Figure 9a. The intervals of the syntonic chromatic scale approximated by multiples of unit intervals, which result from various divisions of the octave into equal parts.
Newton (1665, 108v)
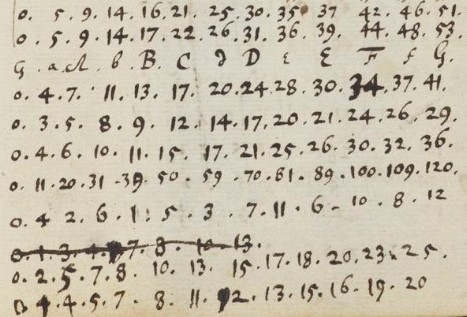
Figure 9b. It is unclear how the almost regular pattern in the fourth row from the bottom (0 4 2 6 1 5 3 7 11 6 10 8 12) is related to the divisions of the octave. Newton (1665, 108r)

Figure 9c. Above: Two versions of 120-EDO with semitones of the sizes 11, 9, 8 resp. 12, 8, 6 units, the latter are equivalent to 6, 4, 3 in 60-EDO. Newton (1665, 106r). Below: A 24-EDO representation with a lesser chromatic semitone of size 0. Newton (1665, 108r).
Why at all should one study tone systems with so many pitches per octave, if the smallest steps are imperceptibly small? From the end of the 15th century to the early 20th century many different limit-5 chromatic and enharmonic systems with up to 53 pitches per octave have been proposed. Among the enharmonic scales given by Athanasius Kircher (1650) there is a scale with 38 pitches per octave, and Arthur von Oettingen (1917) depicts a selection of 53 limit-5 pitches. One reason for the study of fine grained "enharmonic" syntonic scales in the 16th century was the wish to represent the Greek enharmonic tetrachords with their "quarter tones" in limit-5, see Zarlino (1562, 162) 26.
The analysis of the intervals in historical enharmonic scales with 22 or more pitch classes shows that they are much better represented in 118-EDO than in 53-EDO. Since 612-EDO is the coarsest tuning that accounts accurately and consistently for two differently sized commas – the Pythagorean and the syntonic with 12 and 11 units – it is the best base to study tunings which correspond to large coherent regions of the syntonic pitch grid. If the distinction between the Pythagorean and syntonic commas is irrelevant, 53-EDO with "Mercator comma"-units turns out to be the most convenient finite tuning for Pythagorean and syntonic scales. And two successive sounds distant by a Mercator comma are perceptibly different in pitch.To put it differently, whereas look-up tables for exponential functions and logarithms used in astronomy have many thousand entries to cover the range between 1 and 10, musical look-up tables require only 53, 118 or 612 entries to enable their user to calculate the ratios of arbitrary limit 5-intervals within an octave with high precision. Jost Bürgi's exponential table (Bürgi 1620) has the base 1.0001 = 101/23027.002… = 21/6931.818… so that it requires 6,932 entries to cover the range between 1 and 2 of a musical octave. Newton needed only the values of 12 base 10 logarithms, when he determined the optimum bases for musical logarithms and he did not even need numerical values for their bases, 2 ≈ 1.01316 and 2 ≈ 1.00113.
With similar intentions Aristoxenous divided the whole tone into sixty parts in order to compare the many varieties of the Greek diatonic, chromatic and enharmonic tetrachords suggested by different authors. The corresponding meta-system is 360-EDO, if the tone is interpreted as the sixth part of an octave as Vincenzo Galilei assumed (Galilei 1581, 58), so that historically Newton is not completely isolated with his fine-grained division of the octave.
51-EDO and 53-EDO
From the 612-EDO representation of the chromatic scale Newton could determine with fewer parts without extensive calculations. Taking the accuracy of 612-EDO for granted, it can be used to find coarser good equal divisions of the octave by proportionally reducing the 612-EDO representations. It follows from the previous paragraph that the irrational number 21/612, the frequency ratio of the 612-EDO unit, can serve as the common ratio of a geometric series which approximates Newton's syntonic scale more accurately than any other equal division of the octave 27. An idea for the varying quality of the approximations can be obtained by comparing the decimal parts of the numbers in the bottom row of Table 1 with the corresponding decimal parts in the bottom lines (labeled 'direct') of the following Tables 4 and 5 28.
For finding the interval sizes of the 51-EDO scale one is tempted to divide the numbers in the 612-EDO scale by 12 and round the results to the next integer, see the rows labeled "Newton" and "../12" in Table 4. Thereby, a simple rescaling is performed in order to calculate the pitches in 51-EDO from the 612-EDO pitches.
Newton's values for 51-EDO differ at two places from these rescaled values. This is not to be considered a mistake, since with Newton's values all the diatonic semitones (G-A♭, A-B♭, B-C, C♯-D, D-E♭, E-F, F♯-G) measure 5 units, the greater chromatic semitones (A♭-A, C-C♯, F-F♯) measure 4 and the lesser chromatic semitones (B♭-B, E♭-E) measure 2 units each. In other words, the two adjustments create a consistent scale, in which equal syntonic intervals are rendered with equal numbers of 51-EDO units: 7 ⋅ 5 + 3 ⋅ 4 + 2 ⋅ 2 = 51.
The major tones in Newton's 51-EDO scale measure 9 units so that six of them are 3 units larger than an octave. This difference, the 51-EDO equivalent of the Pythagorean comma, is three times as big as the Pythagorean comma 29, so that Newton's 51-EDO representation must be considered a very weak approximation to the syntonic chromatic scale.
| G | A♭ | A | B♭ | B | C | C♯ | D | E♭ | E | F | F♯ | G | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Newton | 0 | 57 | 104 | 161 | 197 | 254 | 301 | 358 | 415 | 451 | 508 | 555 | 612 |
| ../12 | 0 | 4.8 | 8.7 | 13.4 | 16.4 | 21.2 | 25.1 | 29.8 | 34.6 | 37.6 | 42.3 | 46.3 | 51 |
| rounded | 0 | 5 | 9 | 13 | 16 | 21 | 25 | 30 | 35 | 38 | 42 | 46 | 51 |
| Newton | 0 | 5 | 9 | 14 | 16 | 21 | 25 | 30 | 35 | 37 | 42 | 46 | 51 |
| direct | 0 | 4.75 | 8.67 | 13.42 | 16.42 | 21.17 | 25.09 | 29.83 | 34.58 | 37.58 | 42.33 | 46.25 | 51 |
Note: The pitch reference is G = 0 so that the size of the octave is either 612 or 51 units. Newton's 51-EDO representation differs at two places from simple rescaling. The last row in this table shows that rescaling from 612-EDO and direct logarithmic calculation result in the same integer approximations.
If instead only the 612-EDO sizes of the three semitones 57, 47, 36 are divided by 12 and rounded to the next integer, (,,) ≈ (4.8,3.9,3) ≈ (5,4,3), the division of the octave into 53 equal parts is obtained in a natural way because of 7 ⋅ 5 + 3 ⋅ 4 + 2 ⋅ 3 = 53 = 6 ⋅ 9 - 1. In this partition of the octave both the syntonic and the Pythagorean comma measure one unit. The 53-EDO values of the chromatic scale can also be determined correctly by rescaling the 612-EDO values with and rounding the results to the closest integer, see Table 5. The last row of the same table confirms that proportional rescaling gives the same numbers as the direct logarithmic computation. Furthermore, the maximum deviation in the best fit for 53-EDO is only 0.068 units (compared with 0.418 in 51-EDO).
| G | A♭ | A | B♭ | B | C | C♯ | D | E♭ | E | F | F♯ | G | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Newton | 0 | 57 | 104 | 161 | 197 | 254 | 301 | 358 | 415 | 451 | 508 | 555 | 612 |
| ..*(53/612) | 0 | 4.9 | 9.0 | 13.9 | 17.1 | 22.0 | 26.1 | 31.0 | 35.9 | 39.1 | 44 | 48.1 | 53 |
| Newton | 0 | 5 | 9 | 14 | 17 | 22 | 26 | 31 | 36 | 39 | 44 | 48 | 53 |
| direct | 0 | 4.93 | 9.01 | 13.94 | 17.06 | 21.997 | 26.07 | 31.003 | 35.94 | 39.06 | 43.99 | 48.07 | 53 |
41-EDO and 29-EDO
The representation of the chromatic scale in 41-EDO and 29-EDO can be directly obtained from the values of 53-EDO by reducing the semitone sizes evenly, see Table 6. The last row shows that the same procedure cannot be continued down to 17-EDO, since the related lesser chromatic semitones would have size zero.
| G | A♭ | A | B♭ | B | C | C♯ | D | E♭ | E | F | F♯ | G | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 53-EDO | 0 | 5 | 9 | 14 | 17 | 22 | 26 | 31 | 36 | 39 | 44 | 48 | 53 |
| -0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | -10 | -11 | -12 | |
| 41-EDO | 0 | 4 | 7 | 11 | 13 | 17 | 20 | 24 | 28 | 30 | 34 | 37 | 41 |
| -0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | -10 | -11 | -12 | |
| 29-EDO | 0 | 3 | 5 | 8 | 9 | 12 | 14 | 17 | 20 | 21 | 24 | 26 | 29 |
| -0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | -10 | -11 | -12 | |
| 17-EDO | 0 | 2 | 3 | 5 | 5 | 7 | 8 | 10 | 12 | 12 | 14 | 15 | 17 |
Note: The semitone size numbers of 53-EDO are reduced by 1 or 2 units to obtain their values in 41-EDO and 29-EDO. A like reduction by 3 units to obtain 17-EDO would result in chromatic semitones B♭-B and E♭-E of size 0.
This shows that there is no consistent scale with less than 29 units which distinguishes between the three kinds of semitones and preserves their natural order (<<) at the same time. Newton did not consider 65-EDO, 77-EDO and 89-EDO, although they can be derived from 53-EDO in the same way as 41-EDO and 29-EDO, probably because they divide the octave into more parts and give less accurate approximations than 53-EDO.
Overview and classification of Newton's EDOs
The results of my analysis of the remaining scales studied by Newton are summarized in the following. Newton examined only divisions of the octave which assign fixed sizes to the three different semitones. Their sizes and the resulting minor and major tones are listed in Table 7.
| n-EDO | 612 | 51 | 53 | 41 | 29 | 36 | 60 | 120 | 120 | 100 | 100 | 25 | 20 | 15 | 19 | 24 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 25 : 24 (c) | 36 | 2 | 3 | 2 | 1 | 1 | 3 | 6 | 8 | 3 | 1 | 1 | 2 | -1 | 3 | 0 |
| 135 : 128 (b) | 47 | 4 | 4 | 3 | 2 | 2 | 4 | 8 | 9 | 8 | 7 | 3 | 3 | 1 | 2 | 1 |
| 16 : 15 (a) | 57 | 5 | 5 | 4 | 3 | 4 | 6 | 12 | 11 | 10 | 11 | 2 | 1 | 2 | 1 | 3 |
| 10 : 9 (t) | 93 | 7 | 8 | 6 | 4 | 5 | 9 | 18 | 19 | 13 | 12 | 3 | 3 | 1 | 4 | 3 |
| 9 : 8 (T) | 104 | 9 | 9 | 7 | 5 | 6 | 10 | 20 | 20 | 18 | 18 | 5 | 4 | 3 | 3 | 4 |
Note: The numbers highlighted in the EDOs with n = 25 or less indicate inconsistencies within the syntonic scale to be approximated.
Newton's 17 different EDOs can be classified as follows:
- 612, 51, 53, 41, 29: derivation from 612-EDO and 53-EDO
- 59: optimization of the major third or indirect derivation from 120-EDO or 53-EDO
- 24, 36, 60, 120: refinement of 12-EDO / 120: decimal division of the 12-EDO semitone
- 100, 25, 20: decimal division of the octave
- 15, 19, 20, 24, 25: small numbers (relative semitone sizes not respected)
Only, 29-EDO, 41-EDO, 53-EDO and 612-EDO, agree fully with the isolated rounding, which shows that Newton must have determined the representations of the scale by assigning fixed sizes to three independent intervals, e.g., to the three different semitones – at various places in the notebook he used the abbreviations a, b and c for the three semitones and r, s, t for the major tone, the minor tone and the diatonic semitone. Also, the latter three intervals determine the corresponding approximation completely.
Newton did not consider the division into 118 equal parts, which is the closest approximation of his syntonic chromatic scale for octave division between 53-EDO and 612-EDO. He could have found this division, if he had investigated the rejected divisions into 59 parts or the division into 120 parts in greater detail. And he did not consider the accurate and consistent divisions into 65 (= 53 + 1 ⋅ 12), 77 (= 53 + 2 ⋅ 12) and 89 (= 53 + 3 ⋅ 12) parts, perhaps because they use more parts than 53-EDO and are less accurate.
Without logarithms the divisions into 53 equal parts can be found by comparing the Pythagorean comma to the Pythagorean semitone, which are nearly in the size ratio 1 : 4. This approximate ratio was known by Boethius (1867, 293-295: Inst. Mus. III, 14) so that the whole tone, consisting of two Pythagorean semitones ("limmae") and a Pythagorean comma gives 9 units, and the octave – six tones minus a comma – measures6 ⋅ 9 - 1 = 53 units, with a unit interval close to the Pythagorean comma. In fact, the octave measures 55.8 syntonic commas or 51.15 Pythagorean commas, so that Mercator's "artificial comma" is a good average between the two commas, being only marginally greater in magnitude (.475) than the true average'.This explains the accurate Pythagorean and syntonic intervals in 53-EDO.
The division of the octave into 53 equal parts was studied by Nicolaus Mercator at about the same time as Newton or even earlier 30. As Benjamin Wardhaugh (personal communication, 2020) points out, it is not very likely that the two men exchanged ideas about tuning, since Newton at this time was still a student with no public profile. We do not know whether Newton, at the age of 22, was familiar with the aforementioned comparison of the Pythagorean comma to the semitone by Boethius 31.
COMPUTATIONAL ANALYSIS OF ARBITRARY EDO-APPROXIMATIONS
For the computer assisted analysis described in this section, I have created small Java programs with Processing. They generated lists of scales and key figures which I examined with spread sheets. One of these programs determined and analyzed the n-EDO approximations of limit-5 diatonic and chromatic scales for n < 2000, see Appendix_2 (http://hdl.handle.net/1811/92832). This analysis of the least square deviations can be related to Newton's octave divisions.
For this purpose, the diatonic and chromatic scales of just intonation are expressed with ratios to the reference notes C resp. G as follows. The syntonic diatonic scale (limit-5 diatonic scale) has two alternative pitches for the second degree D, so that both the major tone and the minor tone above the key C are present:
| C | D | D | E | F | G | A | B | C |
| 1 | 2 |
The two varieties of D differ by a syntonic comma c (81 : 80). This selection is in accordance with Descartes's definition of the diatonic scale, with the symmetric pattern t-c-t-S-T-t-T-S with which Newton was familiar. The (syntonic) chromatic scale is taken from Newton's notebook (Figure 8) and defined by:
| G | A♭ | A | B♭ | B | C | C♯ | D | E♭ | E | F | F♯ | G |
| 1 | 2 |
For a given value of n (i.e., for the division of the octave into n equal intervals), the program calculates the sizes of all the intervals with respect to the reference note (C resp. G) with the formula n ⋅ log2 and rounds them to the next integer. In the following this procedure is called isolated (logarithmic) rounding, if all the intervals of the diatonic or chromatic scale are determined in this way, see Appendix_3 (http://hdl.handle.net/1811/92832). The column headed dev in the Tables 8 and 9 contain the root mean square (rms) deviations of n ⋅ log2 from the rounded values. This deviation is thus expressed in units of the corresponding n-EDO approximation. The last column dev_c contains the rms-deviation expressed in cent. The cent values naturally converge against 0 for increasing values of n, whereas the deviations with respect to the size of the unit intervals do not. In the following the latter is simply called deviation, if the context is clear, and the root mean square deviation measured in cent, is called cent-deviation.
| n | C | D | D | E | F | G | A | B | C | dev | dev_c |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 12 | 0 | 2 | 2 | 4 | 5 | 7 | 9 | 11 | 12 | 0.1135 | 11.35 |
| 53 | 0 | 8 | 9 | 17 | 22 | 31 | 39 | 48 | 53 | 0.0460 | 1.04 |
| 118 | 0 | 18 | 20 | 38 | 49 | 69 | 87 | 107 | 118 | 0.0373 | 0.38 |
| 559 | 0 | 85 | 95 | 180 | 232 | 327 | 412 | 507 | 559 | 0.0306 | 0.07 |
| 612 | 0 | 93 | 104 | 197 | 254 | 358 | 451 | 555 | 612 | 0.0166 | 0.03 |
| 1783 | 0 | 271 | 303 | 574 | 740 | 1043 | 1314 | 1617 | 1783 | 0.0152 | 0.01 |
| 2513 | 0 | 382 | 427 | 809 | 1043 | 1470 | 1852 | 2279 | 2513 | 0.0134 | 0.006 |
| 4296 | 0 | 653 | 730 | 1383 | 1783 | 2513 | 3166 | 3896 | 4296 | 0.0030 | 0.0008 |
Note: The values in column dev form a monotonically decreasing sequence if indexed by n. There is no longer subset of indices n from 12 to 5000 with this property.
| n | G | A♭ | A | B♭ | B | C | C♯ | D | E♭ | E | F | F♯ | G | dev | dev_c |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 12 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 0.1076 | 10.76 |
| 53 | 0 | 5 | 9 | 14 | 17 | 22 | 26 | 31 | 36 | 39 | 44 | 48 | 53 | 0.0504 | 1.14 |
| 118 | 0 | 11 | 20 | 31 | 38 | 49 | 58 | 69 | 80 | 87 | 98 | 107 | 118 | 0.0325 | 0.33 |
| 612 | 0 | 57 | 104 | 161 | 197 | 254 | 301 | 358 | 415 | 451 | 508 | 555 | 612 | 0.0157 | 0.03 |
| 1783 | 0 | 166 | 303 | 469 | 574 | 740 | 877 | 1043 | 1209 | 1314 | 1480 | 1617 | 1783 | 0.0156 | 0.01 |
| 2513 | 0 | 234 | 427 | 661 | 809 | 1043 | 1236 | 1470 | 1704 | 1852 | 2086 | 2279 | 2513 | 0.0151 | 0.007 |
| 3684 | 0 | 343 | 626 | 969 | 1186 | 1529 | 1812 | 2155 | 2498 | 2715 | 3058 | 3341 | 3684 | 0.0134 | 0.004 |
| 4296 | 0 | 400 | 730 | 1130 | 1383 | 1783 | 2113 | 2513 | 2913 | 3166 | 3566 | 3896 | 4296 | 0.0024 | 0.0007 |
| 559 | 0 | 52 | 95 | 147 | 180 | 232 | 275 | 327 | 379 | 412 | 464 | 507 | 559 | 0.0358 | 0.08 |
Note: The record n = 559 at the bottom is found by the optimization of the diatonic scale (Table 8), but not in the optimization of the chromatic scale (Table 9).
The Tables 8 and 9 list optimal approximations with respect to the rms-deviation (dev) in the following sense. For all integers k less than n the deviation in k-EDO is greater than the deviation in n-EDO. For example, the smallest number for which the deviations of the chromatic and the diatonic scale are smaller than the deviations for 12 is 53. And between 53-EDO and 118-EDO there is no equal division k-EDO with a deviation smaller than the deviation for 53-EDO. This procedure produces maximal monotonically decreasing sequences of deviations.
The rankings created by this optimization algorithm are very similar across all sets of syntonic pitches tested, which comprised the full chromatic and diatonic scales, the major triad and the combination of the diatonic semitone with the major and minor tones 32. This is not totally unexpected, since the syntonic system (limit-5 tuning) is generated by Pythagorean fifths and syntonic major thirds (modulo octave). The deviations for the diatonic scale, the chromatic scale as well as major thirds and fifths (the perfect major triad) for n = 12 to 133 are visualized in Figure 10.
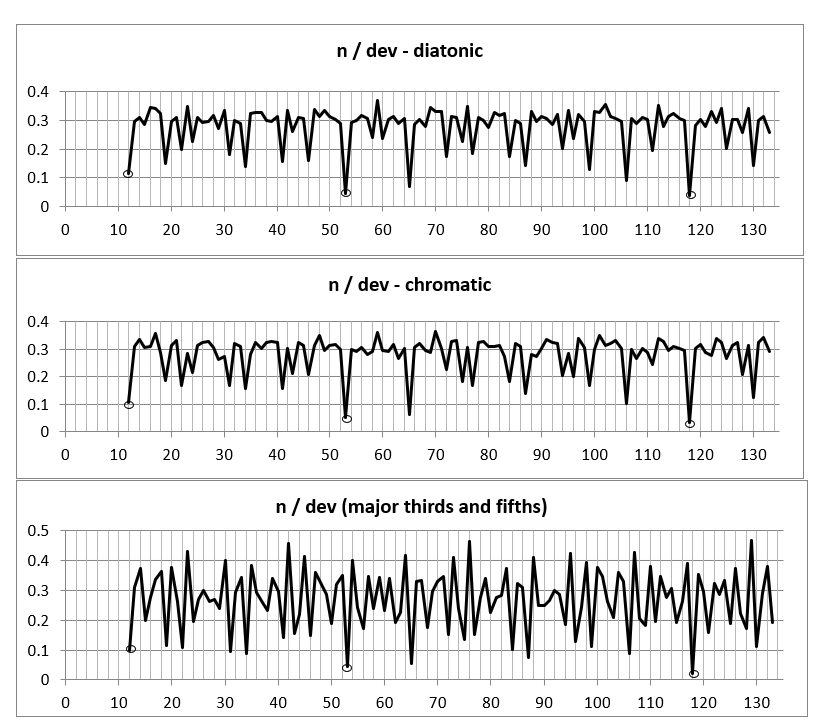
Figure 10. The rms-deviations of the diatonic scale, the chromatic scale and major triads (major thirds and fifths) for n = 12 to 133 exhibit similar patterns. The minima for n = 12, 53 and 118 are highlighted with small circles. Notice that pronounced minima also occur at n = 53 ± 12 and at n = 118 ± 12.
Log-compatibility and consistency
Newton's syntonic chromatic scale has three different semitones, the diatonic semitone (16 : 15 of 111.73 cent), the greater chromatic semitone (135 : 128 of 92.18 cent) and the lesser chromatic semitone (25 : 24 of 70.67 cent). His scale with reference note G has seven diatonic semitones a, three greater chromatic semitones b and two lesser chromatic semitones c, and the octave is filled by the semitone-pattern a-b-a-c-a-b-a-a-c-a-b-a 33.
In the following, a chromatic n-EDO scale is called consistent, if the semitones of the same kind are rendered as equal intervals, and it is called strongly consistent, if it is consistent and the condition 2c > a > b > c is satisfied, so that the relative size order of the three semitones is respected and the lesser chromatic semitone c is greater than half a diatonic semitone a 34. Scales agreeing with the directly rounded logarithms are called log-compatible. The smallest positive integers (a, b, c) with 2c > a > b are (5, 4, 3). With these values for a, b and c the 7 diatonic, the 3 greater and the 2 lesser chromatic semitones add up to an octave of 53 units (53 = 7 ⋅ 5 + 3 ⋅ 4 + 2 ⋅ 3). Since the isolated roundings of Newton's syntonic chromatic scale agree with the consistent 53-EDO representation, 53-EDO provides the coarsest strongly consistent and log-compatible chromatic scale.
In order to classify the chromatic scales for n up to 1200 "consistency levels" as defined in Table 10 are used. Hereby, level 0 is equivalent with strong consistency. These definitions quantify the similarity of interval size relationships between the approximating EDO-scales and Newton's syntonic chromatic scale. The restrictions become gradually weaker for increasing consistency levels. True syntonic chromatic scales would have consistency level 0, their approximation through 12-EDO have consistency level 3, because 12-EDO does not distinguish between different semitones and has a = b = c.
| cns-level | condition |
|---|---|
| 0 | 2c > a > b > c |
| 1 | a > b > c and 2c ≤ a |
| 2 | a > b = c |
| 3 | a = b ≥ c |
| 4 | Not a ≥ b ≥ c |
Note: The variables a, b and c are the sizes of the diatonic, the greater chromatic and the lesser chromatic semitones.
For n ≤ 1200 there are 374 divisions of the octave into n equal intervals with log-compatible chromatic scales. The lowest deviations for scales with consistency levels > 0 occurs at 12-EDO 35, 34-EDO and 41-EDO. The maximum deviation occurs at 306-EDO (306 = ⋅ 612). 53-EDO and 65-EDO are the only divisions of the octave into less than 100 equal parts with a relative deviation lower than that of 12-EDO.
53, 118 AND 612 – A GENERATOR SYSTEM AND ITS GEOMETRIC INTERPRETATION
A close inspection of the numbers n with small deviations between the best EDO fit and the syntonic chromatic scale reveals that they are in a close relationship to 612, 118 and 53, the numbers with the smallest relative deviations. The deviations for 53-EDO, 118-EDO and 612-EDO are visualized in Figure 11. The analysis of the data explored in this section shows that all the numbers n up to 1200 with a log-compatible syntonic n-EDO scale can be written in the format n = 612x + 118y + 53z, where x, y and z are integers close to 0. The number n of the 32 scales with the lowest deviations can be written in this format with 0 ≤ x ≤ 2, -2 ≤ y ≤ 2 and -2 ≤ z ≤ 1.
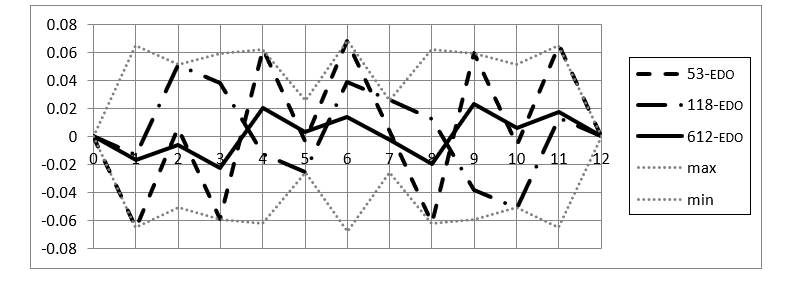
Figure 11. Relative deviations of the best fit for 53-EDO, 118-EDO and 612-EDO. The notes of the chromatic scale are numbered in horizontal direction from 0 to 12 with pitch reference G = 0, 12. 118-EDO has smallest deviations for minor second (1), major third (4), minor sixth (8) and major seventh (11) and greatest deviations for major second (2), fourth (5), fifth (7) and minor seventh (10). The envelopes min/max refer to absolute values.
Therefore 53-EDO, 118-EDO and 612-EDO form a kind of generator system for log-compatible consistent scales. More precisely, the correct sizes of the n-EDO intervals can be linearly combined from the corresponding sizes in 53-EDO, 118-EDO and 612-EDO for all log-compatible scales with n ≤ 1200.
If a given n can be written as n = 612x + 118y + 53z, where -1 ≤ x ≤ 3, -9 ≤ y ≤ 10 and -8 ≤ z ≤ 7, the n-EDO sizes of the diatonic semitone a and the chromatic semitones b and c can be calculated with the formulas a = x ⋅ 57 + y ⋅ 11 + z ⋅ 5, b = x ⋅ 47 + y ⋅ 9 + z ⋅ 4 and c = x ⋅ 36 + y ⋅ 7 + z ⋅ 3 so that the sizes of the three semitones a, b and c are uniquely determined and hence the entire chromatic scale. In other words, the log-compatible n-EDO representation (for arbitrary values of n ≤ 1200) of the syntonic chromatic scale can be determined without using logarithms – just on base of the values of 53-EDO, 118-EDO and 612-EDO. The main task for a given n is to express it as a suitable linear combination of 612, 118 and 53. Parts of the results of the corresponding calculations are shown in Table 11.
The following example uses n = 935 and shows how the n-EDO representations of Newton's chromatic scale can be calculated by hand from the first four columns of Table 11: Because 935 can be written as 935 = 2 ⋅ 612 - 2 ⋅ 118 - 1 ⋅ 53 the coordinates for 935-EDO (dev rank 21) are (x,y,z) = (2,-2,-1) By substituting them into the formulas
- a = x ⋅ 57 + y ⋅ 11 + z ⋅ 5
- b = x ⋅ 47 + y ⋅ 9 + z ⋅ 4
- c = x ⋅ 36 + y ⋅ 7 + z ⋅ 3,
the sizes of the 935-EDO semitones can be obtained as follows:
- a = 2 ⋅ 57 + (-2) ⋅ 11 + (-1) ⋅ 5 = 87
- b = 2 ⋅ 47 + (-2) ⋅ 9 + (-1) ⋅ 4 = 72
- c = 2 ⋅ 36 + (-2) ⋅ 7 + (-1) ⋅ 3 = 55
With these values of a, b and c and the semitone-pattern a-b-a-c-a-b-a-a-c-a-b-a the calculation of the 935-EDO representation of Newton's chromatic scale can be calculated as a cumulative sum:
- a = 87
- a + b = 87 + 72 = 129
- a + b + a = 129 + 87 = 246
- a + b + a + c = 246 + 55 = 301
- …
| n | x | y | z | rnk | a | b | c | scale | dev_u | cmpt | cns | dev_rnk |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 612 | 1 | 0 | 0 | 1 | 57 | 47 | 36 | 0 57 104 161 197 254 301 358 415 451 508 555 612 | 0.0157 | 0 | 0 | 1 |
| 1171 | 2 | 0 | -1 | 5 | 109 | 90 | 69 | 0 109 199 308 377 486 576 685 794 863 972 1062 1171 | 0.0227 | 0 | 0 | 2 |
| 730 | 1 | 1 | 0 | 2 | 68 | 56 | 43 | 0 68 124 192 235 303 359 427 495 538 606 662 730 | 0.0306 | 0 | 0 | 3 |
| 118 | 0 | 1 | 0 | 1 | 11 | 9 | 7 | 0 11 20 31 38 49 58 69 80 87 98 107 118 | 0.0325 | 0 | 0 | 4 |
| 559 | 1 | 0 | -1 | 2 | 52 | 43 | 33 | 0 52 95 147 180 232 275 327 379 412 464 507 559 | 0.0358 | 0 | 0 | 5 |
| 494 | 1 | -1 | 0 | 2 | 46 | 38 | 29 | 0 46 84 130 159 205 243 289 335 364 410 448 494 | 0.0408 | 0 | 0 | 6 |
| 1053 | 2 | -1 | -1 | 6 | 98 | 81 | 62 | 0 98 179 277 339 437 518 616 714 776 874 955 1053 | 0.0462 | 0 | 0 | 7 |
| 677 | 1 | 1 | -1 | 3 | 63 | 52 | 40 | 0 63 115 178 218 281 333 396 459 499 562 614 677 | 0.0463 | 0 | 0 | 8 |
| 441 | 1 | -1 | -1 | 3 | 41 | 34 | 26 | 0 41 75 116 142 183 217 258 299 325 366 400 441 | 0.0503 | 0 | 0 | 9 |
| 53 | 0 | 0 | 1 | 1 | 5 | 4 | 3 | 0 5 9 14 17 22 26 31 36 39 44 48 53 | 0.0504 | 0 | 0 | 10 |
| 1106 | 2 | -1 | 0 | 5 | 103 | 85 | 65 | 0 103 188 291 356 459 544 647 750 815 918 1003 1106 | 0.0526 | 0 | 0 | 11 |
| 171 | 0 | 1 | 1 | 2 | 16 | 13 | 10 | 0 16 29 45 55 71 84 100 116 126 142 155 171 | 0.0585 | 0 | 0 | 12 |
| 848 | 1 | 2 | 0 | 5 | 79 | 65 | 50 | 0 79 144 223 273 352 417 496 575 625 704 769 848 | 0.0611 | 0 | 0 | 13 |
| 65 | 0 | 1 | -1 | 2 | 6 | 5 | 4 | 0 6 11 17 21 27 32 38 44 48 54 59 65 | 0.0614 | 0 | 0 | 14 |
| 236 | 0 | 2 | 0 | 4 | 22 | 18 | 14 | 0 22 40 62 76 98 116 138 160 174 196 214 236 | 0.0649 | 0 | 0 | 15 |
| 665 | 1 | 0 | 1 | 2 | 62 | 51 | 39 | 0 62 113 175 214 276 327 389 451 490 552 603 665 | 0.0656 | 0 | 0 | 16 |
| 783 | 1 | 1 | 1 | 3 | 73 | 60 | 46 | 0 73 133 206 252 325 385 458 531 577 650 710 783 | 0.0694 | 0 | 0 | 17 |
| 795 | 1 | 2 | -1 | 6 | 74 | 61 | 47 | 0 74 135 209 256 330 391 465 539 586 660 721 795 | 0.0715 | 0 | 0 | 18 |
| 1118 | 2 | 0 | -2 | 8 | 104 | 86 | 66 | 0 104 190 294 360 464 550 654 758 824 928 1014 1118 | 0.0717 | 0 | 0 | 19 |
| 376 | 1 | -2 | 0 | 5 | 35 | 29 | 22 | 0 35 64 99 121 156 185 220 255 277 312 341 376 | 0.072 | 0 | 0 | 20 |
| 935 | 2 | -2 | -1 | 9 | 87 | 72 | 55 | 0 87 159 246 301 388 460 547 634 689 776 848 935 | 0.0765 | 0 | 0 | 21 |
| 323 | 1 | -2 | -1 | 6 | 30 | 25 | 19 | 0 30 55 85 104 134 159 189 219 238 268 293 323 | 0.0767 | 0 | 0 | 22 |
| 547 | 1 | -1 | 1 | 3 | 51 | 42 | 32 | 0 51 93 144 176 227 269 320 371 403 454 496 547 | 0.0767 | 0 | 0 | 23 |
| 289 | 0 | 2 | 1 | 5 | 27 | 22 | 17 | 0 27 49 76 93 120 142 169 196 213 240 262 289 | 0.0801 | 0 | 0 | 24 |
| 1000 | 2 | -1 | -2 | 9 | 93 | 77 | 59 | 0 93 170 263 322 415 492 585 678 737 830 907 1000 | 0.0811 | 0 | 0 | 25 |
| 988 | 2 | -2 | 0 | 8 | 92 | 76 | 58 | 0 92 168 260 318 410 486 578 670 728 820 896 988 | 0.0816 | 0 | 0 | 26 |
| 183 | 0 | 2 | -1 | 5 | 17 | 14 | 11 | 0 17 31 48 59 76 90 107 124 135 152 166 183 | 0.0843 | 0 | 0 | 27 |
| 506 | 1 | 0 | -2 | 5 | 47 | 39 | 30 | 0 47 86 133 163 210 249 296 343 373 420 459 506 | 0.0861 | 0 | 0 | 28 |
| 901 | 1 | 2 | 1 | 6 | 84 | 69 | 53 | 0 84 153 237 290 374 443 527 611 664 748 817 901 | 0.0862 | 0 | 0 | 29 |
| 624 | 1 | 1 | -2 | 6 | 58 | 48 | 37 | 0 58 106 164 201 259 307 365 423 460 518 566 624 | 0.0919 | 0 | 0 | 30 |
| 388 | 1 | -1 | -2 | 6 | 36 | 30 | 23 | 0 36 66 102 125 161 191 227 263 286 322 352 388 | 0.0921 | 0 | 0 | 31 |
| 1159 | 2 | -1 | 1 | 6 | 108 | 89 | 68 | 0 108 197 305 373 481 570 678 786 854 962 1051 1159 | 0.0922 | 0 | 0 | 32 |
| 966 | 1 | 3 | 0 | 10 | 90 | 74 | 57 | 0 90 164 254 311 401 475 565 655 712 802 876 966 | 0.0929 | 0 | 0 | 33 |
| 354 | 0 | 3 | 0 | 9 | 33 | 27 | 21 | 0 33 60 93 114 147 174 207 240 261 294 321 354 | 0.0974 | 0 | 0 | 34 |
| 429 | 1 | -2 | 1 | 6 | 40 | 33 | 25 | 0 40 73 113 138 178 211 251 291 316 356 389 429 | 0.0979 | 0 | 0 | 35 |
| 882 | 2 | -2 | -2 | 12 | 82 | 68 | 52 | 0 82 150 232 284 366 434 516 598 650 732 800 882 | 0.1006 | 0 | 0 | 36 |
| 106 | 0 | 0 | 2 | 4 | 10 | 8 | 6 | 0 10 18 28 34 44 52 62 72 78 88 96 106 | 0.1009 | 0 | 0 | 37 |
| 913 | 1 | 3 | -1 | 11 | 85 | 70 | 54 | 0 85 155 240 294 379 449 534 619 673 758 828 913 | 0.1009 | 0 | 0 | 38 |
| 258 | 1 | -3 | 0 | 10 | 24 | 20 | 15 | 0 24 44 68 83 107 127 151 175 190 214 234 258 | 0.104 | 0 | 0 | 39 |
| 224 | 0 | 1 | 2 | 5 | 21 | 17 | 13 | 0 21 38 59 72 93 110 131 152 165 186 203 224 | 0.1043 | 0 | 0 | 40 |
| 205 | 1 | -3 | -1 | 11 | 19 | 16 | 12 | 0 19 35 54 66 85 101 120 139 151 170 186 205 | 0.1065 | 0 | 0 | 41 |
| 407 | 0 | 3 | 1 | 10 | 38 | 31 | 24 | 0 38 69 107 131 169 200 238 276 300 338 369 407 | 0.1073 | 0 | 0 | 42 |
| 12 | 0 | 1 | -2 | 5 | 1 | 1 | 1 | 0 1 2 3 4 5 6 7 8 9 10 11 12 | 0.1076 | 0 | 3 | 43 |
| 742 | 1 | 2 | -2 | 9 | 69 | 57 | 44 | 0 69 126 195 239 308 365 434 503 547 616 673 742 | 0.1076 | 0 | 0 | 44 |
| 270 | 1 | -2 | -2 | 9 | 25 | 21 | 16 | 0 25 46 71 87 112 133 158 183 199 224 245 270 | 0.108 | 0 | 0 | 45 |
| 817 | 2 | -3 | -1 | 14 | 76 | 63 | 48 | 0 76 139 215 263 339 402 478 554 602 678 741 817 | 0.1081 | 0 | 0 | 46 |
| 1019 | 1 | 3 | 1 | 11 | 95 | 78 | 60 | 0 95 173 268 328 423 501 596 691 751 846 924 1019 | 0.1103 | 0 | 0 | 47 |
| 301 | 0 | 3 | -1 | 10 | 28 | 23 | 18 | 0 28 51 79 97 125 148 176 204 222 250 273 301 | 0.112 | 0 | 0 | 48 |
| 1041 | 2 | -2 | 1 | 9 | 97 | 80 | 61 | 0 97 177 274 335 432 512 609 706 767 864 944 1041 | 0.1121 | 0 | 0 | 49 |
| 870 | 2 | -3 | 0 | 13 | 81 | 67 | 51 | 0 81 148 229 280 361 428 509 590 641 722 789 870 | 0.1125 | 0 | 0 | 50 |
| 718 | 1 | 0 | 2 | 5 | 67 | 55 | 42 | 0 67 122 189 231 298 353 420 487 529 596 651 718 | 0.1159 | 0 | 0 | 51 |
| 342 | 0 | 2 | 2 | 8 | 32 | 26 | 20 | 0 32 58 90 110 142 168 200 232 252 284 310 342 | 0.1171 | 0 | 0 | 52 |
| 836 | 1 | 1 | 2 | 6 | 78 | 64 | 49 | 0 78 142 220 269 347 411 489 567 616 694 758 836 | 0.1174 | 0 | 0 | 53 |
| 1065 | 2 | 0 | -3 | 13 | 99 | 82 | 63 | 0 99 181 280 343 442 524 623 722 785 884 966 1065 | 0.1218 | 0 | 0 | 54 |
| 130 | 0 | 2 | -2 | 8 | 12 | 10 | 8 | 0 12 22 34 42 54 64 76 88 96 108 118 130 | 0.1228 | 0 | 0 | 55 |
| 600 | 1 | -1 | 2 | 6 | 56 | 46 | 35 | 0 56 102 158 193 249 295 351 407 442 498 544 600 | 0.1233 | 0 | 0 | 56 |
| 311 | 1 | -3 | 1 | 11 | 29 | 24 | 18 | 0 29 53 82 100 129 153 182 211 229 258 282 311 | 0.1241 | 0 | 0 | 57 |
| 1084 | 1 | 4 | 0 | 17 | 101 | 83 | 64 | 0 101 184 285 349 450 533 634 735 799 900 983 1084 | 0.1251 | 0 | 0 | 58 |
| 1183 | 2 | 1 | -3 | 14 | 110 | 91 | 70 | 0 110 201 311 381 491 582 692 802 872 982 1073 1183 | 0.1252 | 0 | 0 | 59 |
| 764 | 2 | -3 | -2 | 17 | 71 | 59 | 45 | 0 71 130 201 246 317 376 447 518 563 634 693 764 | 0.1256 | 0 | 0 | 60 |
| … | … | … | ||||||||||
| 1083 | 5 | -19 | 5 | 411 | 101 | 84 | 62 | 0 101 185 286 348 449 533 634 735 797 898 982 1083 | 0.734 | 6 | 0 | 1188 |
| 83 | 3 | -18 | 7 | 382 | 8 | 7 | 3 | 0 8 15 23 26 34 41 49 57 60 68 75 83 | 0.7356 | 6 | 1 | 1189 |
| 88 | -3 | 19 | -6 | 406 | 8 | 6 | 7 | 0 8 14 22 29 37 43 51 59 66 74 80 88 | 0.7359 | 6 | 4 | 1190 |
| 1088 | -1 | 18 | -8 | 389 | 101 | 83 | 66 | 0 101 184 285 351 452 535 636 737 803 904 987 1088 | 0.7401 | 6 | 0 | 1191 |
| 524 | 4 | -19 | 6 | 413 | 49 | 41 | 29 | 0 49 90 139 168 217 258 307 356 385 434 475 524 | 0.7479 | 6 | 0 | 1192 |
| 695 | 4 | -18 | 7 | 389 | 65 | 54 | 39 | 0 65 119 184 223 288 342 407 472 511 576 630 695 | 0.7484 | 6 | 0 | 1193 |
| 647 | -2 | 19 | -7 | 414 | 60 | 49 | 40 | 0 60 109 169 209 269 318 378 438 478 538 587 647 | 0.7508 | 6 | 0 | 1194 |
| 476 | -2 | 18 | -8 | 392 | 44 | 36 | 30 | 0 44 80 124 154 198 234 278 322 352 396 432 476 | 0.753 | 6 | 0 | 1195 |
| 1136 | 5 | -19 | 6 | 422 | 106 | 88 | 65 | 0 106 194 300 365 471 559 665 771 836 942 1030 1136 | 0.7599 | 6 | 0 | 1196 |
| 35 | -3 | 19 | -7 | 419 | 3 | 2 | 4 | 0 3 5 8 12 15 17 20 23 27 30 32 35 | 0.7632 | 6 | 4 | 1197 |
| 577 | 4 | -19 | 7 | 426 | 54 | 45 | 32 | 0 54 99 153 185 239 284 338 392 424 478 523 577 | 0.7757 | 6 | 0 | 1198 |
| 594 | -2 | 19 | -8 | 429 | 55 | 45 | 37 | 0 55 100 155 192 247 292 347 402 439 494 539 594 | 0.7798 | 6 | 0 | 1199 |
| 1189 | 5 | -19 | 7 | 435 | 111 | 92 | 68 | 0 111 203 314 382 493 585 696 807 875 986 1078 1189 | 0.7883 | 6 | 0 | 1200 |
The numbers 53 and 118 are relatively prime. Therefore, every integer can be written in the format n = x ⋅ 53 + y ⋅ 118 36. It is important to note that the strong restrictions on the coefficients x, y, z are responsible for the feature that the intervals of the log-compatible consistent chromatic scales can be calculated as described. For example, if the condition on z were weakened to -8 ≤ z ≤ 8, the numbers 306 and 918 could be written in two ways as combinations of 612, 118 and 53:
306 = -118 + 8 ⋅ 53 = 612 + 118 - 8 ⋅ 53 and 918 = 612 - 118 + 8 ⋅ 53 = 2 ⋅ 612 + 118 - 8 ⋅ 53
Only the combinations with z = -8 result in the correct log-compatible semitones, if the formulas for a, b and c are applied. Newton's chromatic scale has a particularly weak approximation in 306-EDO, although it is well suited to approximate Pythagorean tuning 37, and also 918-EDO has very large deviations.
The coordinates highlighted grey in Table 11 are located in the smallest cuboid of Figure 12. The column "rnk" (rank) is calculated with x2 + y2 + z2. The incompatibility index cmpt measures the total deviations from the scale defined through direct log-approximation in n-EDO units. For the definition of the consistency levels cns, see Table 10. The integer triplets (x,y,z) correspond to points in a three-dimensional space. It can be shown that within a cuboid grid of the dimensions 7 × 38 × 15 38 the representation of a number n in the format n = x ⋅ 612 + y ⋅ 118 + z ⋅ 53 is unique and that there are no larger cuboids with this property. The results of the geometrical analysis are summarized and visualized in Figure 12.
Figure 12. Four nested cuboids for n up to 1200. They are defined by the following ranges of x, y and z.
[0, 2][-2, 2][-2, 1]: 60 points; contains the numbers n of the 32 scales with the lowest deviations
[-1, 3][-9, 10][-8, 7]: 1600 points; contains the numbers n of the 374 compatible scales
[-2, 5][-19, 19][-8, 7]: 4992 points; maximum cuboid with unique representation of n (1153 scales)
[-3, 5][-19, 19][-8, 7]: 5616 points; contains all numbers n up to 1200; 12 ambiguous representations
The incompatibility index (cmpt) measures the deviation of a given representation of the syntonic chromatic scale from the best logarithmic pitch values. It is defined as the sum of the individual absolute deviations in n-EDO units, so that an index of 0 is perfect compatibility. There are 372 numbers n between 12 and 1200 with the incompatibility index 0, which means that the related scales agree with the direct logarithmic approximations, and 13 scales have the maximum log-incompatibility index of 7.
There are 356 scales with n between 12 and 1200 which are strongly consistent and log-compatible at the same time. Only 16 compatible scales have consistency levels greater than 0 – none of these values is greater than 3. The corresponding octave dividers n are listed in Table 12.
| cns | cmpt | n |
|---|---|---|
| 1 | 0 | 29, 41, 63, 82 |
| 2 | 0 | 7, 19, 31, 43, 55 |
| 3 | 0 | 10, 12, 22, 24, 34, 36, 46, 56, 58 |
The lowest deviation 0.273 for a log-incompatible scale occurs at n = 920 and the highest deviation of 0.3912 for a log-compatible scale at n = 306. In other words, the root mean square deviation does not fully separate compatible from incompatible scales. It is decisive only for deviations less than 0.273 and for deviations greater than 0.3912.
A simple ranking of the representations n = x ⋅ 512 + y ⋅ 118 + z ⋅ 53 is defined by the Euclidean norm, d = the distance of the point (x,y,z) from the origin (0, 0, 0) and it corresponds to the square root of the column rnk in Table 11. Low values of d correlate to low deviations (dev) of the n-EDO chromatic scales from the syntonic chromatic scale. The graphs in Figures 13a/13b show that the coordinates x, y, z of a number n can be used to estimate the quality of the fit of an n-EDO system with the syntonic chromatic scale. However, there is no monotone relationship between Euclidean norms of these points and the corresponding root mean square deviations.
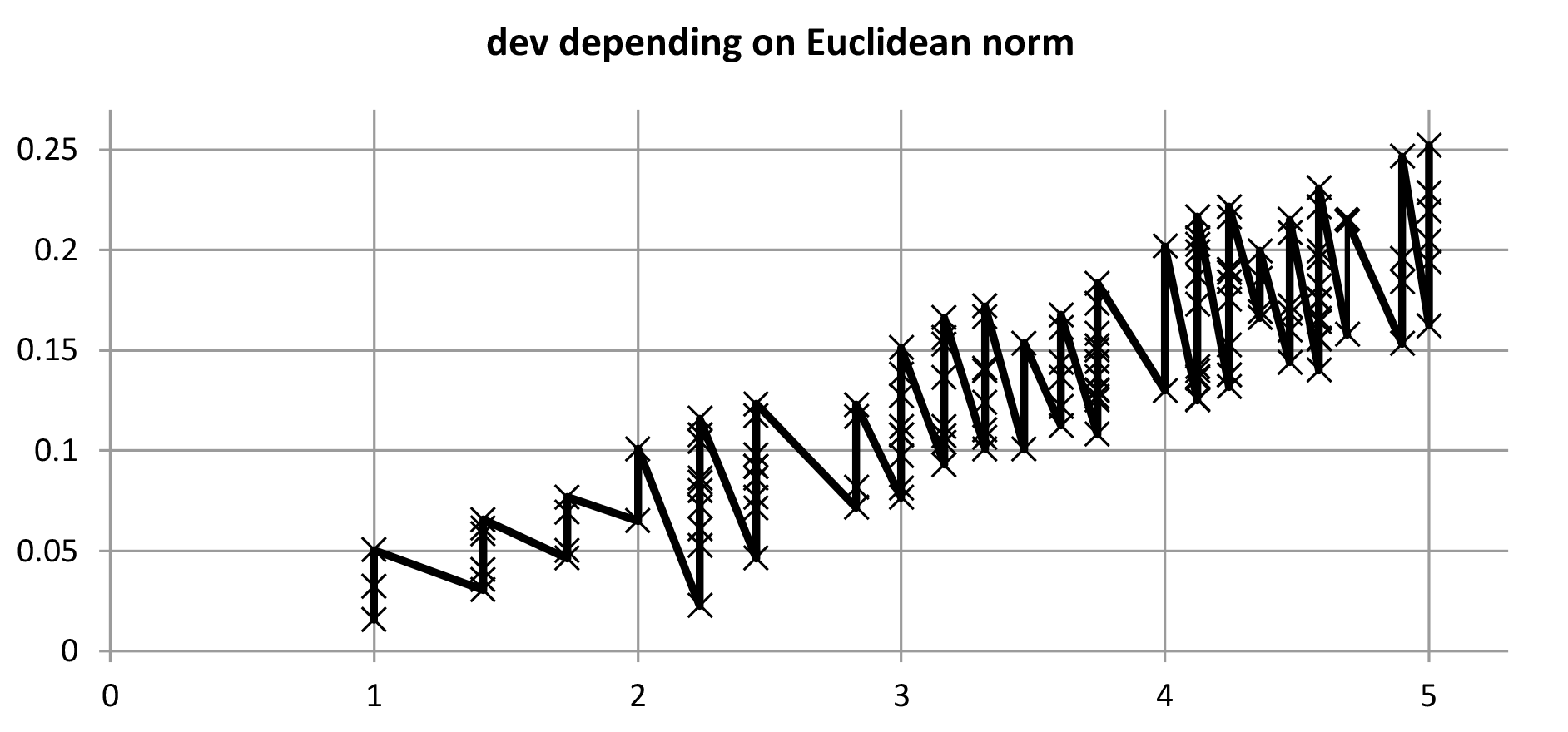
Figure 13a. The horizontal axis of this plot measures the distance of points (x, y, z) from the origin (0, 0, 0), and the vertical measures deviations in n-EDO fits. Points on the same vertical line are located on the same spheres about the origin. Neither the related coordinates nor the corresponding numbers n of the points between the spheres of radius 1 and 5 are indicated. The three points on the unit sphere represent the best EDOs with n = 53, n = 118 and n = 612.
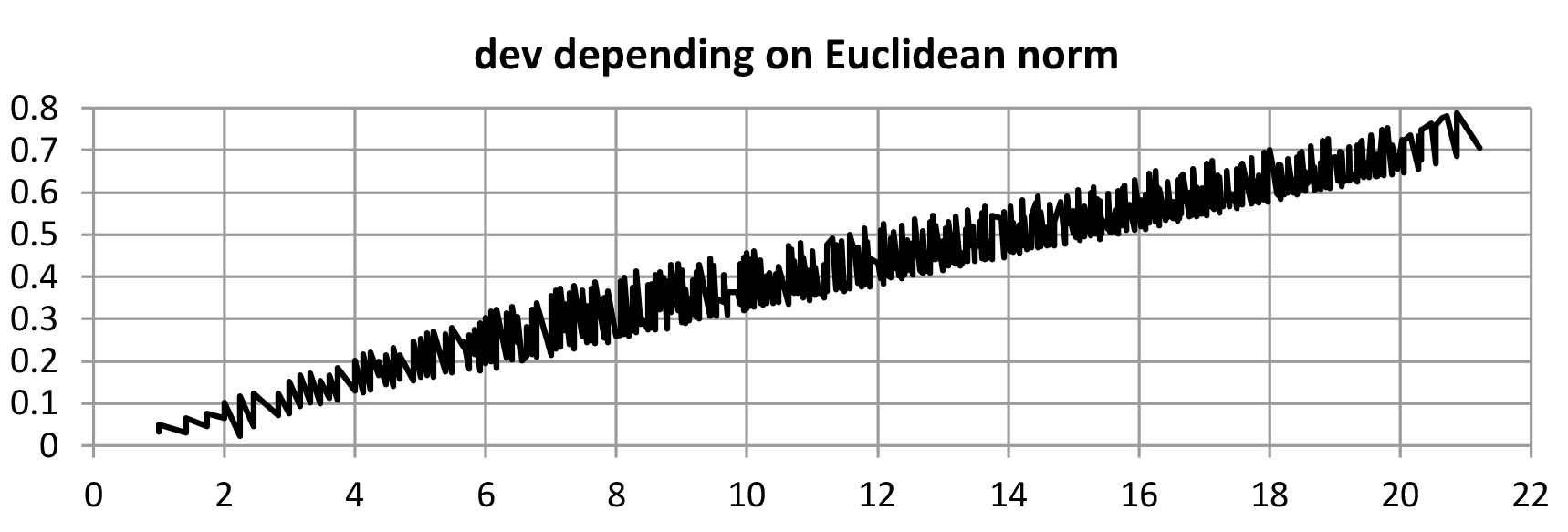
Figure 13b. As Figure 13a but with sphere radiuses up to 21. The configuration is in a good linear correlation.
The two curves in Figure 14 show that the Euclidean norms d = of n = x ⋅ 512 + y ⋅ 118 + z ⋅ 53 (norm: blue) and the deviations of their n-EDO representation from the syntonic chromatic scale (rms_u: red) form very similar patterns. This means that the coordinates (x, y, z) explain the quasi-chaotic dependence on n of the deviations to a wide extent. Both graphs have pronounced minima at 12, 53, 53 ± 12 as well as at 118, 118 ± 12. Some of the strong maxima (indicating inaccurate approximations) occur at 47, 47 ± 12. Recall that 118 = 2 · 53 + 12 = 65 + 53 = 2 · 59 and that the poor 59 (rejected by Newton, see Figure 9a), is exactly in the middle between the pronounced minima at 53 and 65.
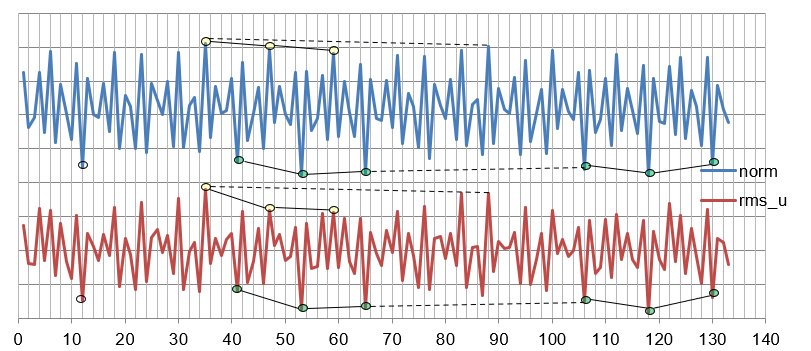
Figure 14. The diagram shows the Euclidean norm (above) of the combinations n = x ⋅ 612 + y ⋅ 118 + z ⋅ 53 and the root mean square deviations of the corresponding consistent n-EDO representation from the syntonic chromatic scale for values of n < 134. Pronounced maxima and minima are highlighted. Maxima correspond to weak and minima to accurate approximations 39.
CONCLUSION
The controversies about syntonic pitch systems and their many ambiguities, as well as the presence of various tempered tunings in the 16th century and later, demanded mathematical skills and powerful tools to compare the related scales and the sizes of the many different intervals efficiently. Accurate tables of logarithms were published in the early 17th century. The use of equal divisions of the octave to measure pitch systems was advanced by Simon Stevin, Marin Mersenne, Nicolaus Mercator, Christiaan Huygens, Isaac Newton and others. The basic idea was to find fine grained "meta-scales" (lowest common denominators) which could express the scales under consideration as subsets very accurately. Newton found two of the three best meta-scales for limit-5 chromatic scales among the equal divisions of the octave with less than 1783 parts.
It is unlikely that the division of the octave into 612 equal parts could have been found without using a logarithm table. However, the division into 53 parts, which is at the same time an optimum for the Pythagorean tuning, could have been found with the knowledge of Boethius. Jacobus Leodiensis in the 14th century proposed a monochord of 53 commas only, a scale with 41 Pythagorean commas and 12 intervals a little smaller 40. My tentative reconstruction of Newton's implicit line of reasoning shows how his various chromatic EDO-approximations can be derived from the 612-EDO representation of the chromatic scale with no need for further logarithms.
The reconstruction of Newton's approach to the tuning problem led to some more general mathematical considerations in the final part of this article. I have shown that the optimum divisions of the octave into 53, 118 and 612 equal parts can be used to generate a comprehensive collection of consistent n-EDO scales for arbitrary divisions of the octave with up to n = 1200 equal parts. This collection contains the scales which agree with direct rounding as a subset. The interpretation of the related numbers n as points in a three-dimensional space revealed an almost linear relationship between their distance from the origin and the quality of the related n-EDO representation of the syntonic chromatic scale. The required calculations rely only on the knowledge of three optimum equal divisions, 53-EDO, 118-EDO and 612-EDO – the key to the large data sets added to this text is hidden in Newton's analysis of the chromatic scale given in Figure 6a.
ACKNOWLEDGEMENTS
This text is based on research made for the project "Sound Colour Space – A Virtual Museum" (2015-2016) at Zurich University of the Arts, funded by the Swiss National Science Foundation (105216_156979). The author wishes to thank Martin Neukom, Benjamin Wardhaugh and Roman Oberholzer for their critical and helpful comments. Furthermore, the insightful comments and suggestions by the reviewers helped a lot to improve my contribution and find its final form. This article was copyedited by Matthew Moore and layout edited by Diana Kayser.
NOTES
-
Correspondence can be addressed to: Dr. Daniel Muzzulini, Bläsiring 42, CH-4057 Basel, daniel@muzzulini.ch.
Return to Text -
Wardhaugh (2013, pp. 85-113). The College Notebook (MS Add.4000), Cambridge University Library, Manuscript 225, is also published online <http://cudl.lib.cam.ac.uk/view/MS-ADD-04000/1> [visited 2020-04-28]
Return to Text -
EDO stands for Equal Division of the Octave; 12-EDO is equal temperament with 12 pitches per octave.
Return to Text -
Comparable statements holding "to a great extent" are frequently given in perceptual psychology, where some (two or three) main factors are determined that would explain a complex phenomenon such as musical timbre by projecting experimental data to a low dimensional structure.
Return to Text -
A monochord is an experimental device (or musical instrument) with a single string that can be divided with moveable bridges in order to study the relationships between musical intervals.
Return to Text -
This is a misleading designation, because the Pythagorean chromatic and enharmonic genera and systems (as for example described and transmitted by Boethius) had interval ratios containing higher prime numbers. In the course of the history they disappeared and the medieval modes were usually constructed on base of proper diatonic tetrachords and hexachords only.
Return to Text -
The full Greek systems (systema teleion) have two different octaves; only the upper octave contains both B♭ and B.
Return to Text -
The combinations lead to just minor thirds (6 : 5) and two different whole tone steps (9 : 8 and 10 : 9).
Return to Text -
Vincenzo Galilei and Gioseffo Zarlino in the 16th century used the term "Sintono di Tolomei" for the just intonation diatonic scale. Limit-5 pitches of the same name differ by syntonic commas, which are a little smaller than Pythagorean commas.
Return to Text -
One of these grids uses three rows of fifths, see Wardhaugh (2013, p. 161, p. 227)
Return to Text -
The use of musical number triangles in historical sources is discussed in Muzzulini (2015, 212-215)
Return to Text -
The continued fractions expansions are independent of the base of the underlying number system. Irrational numbers correspond with infinite continued fractions (Euclid's algorithm does not come to an end for irrational ratios), cf. Schechter (1980). The convergence of the continued fractions approximation to a given irrational number is comparably slow.
Return to Text -
It follows from Proposition 3 of the Euclidean "Sectio canonis" (Barker Ed. 1989, p. 195; Lindley & Turner-Smith 1993, pp. 228-229).
Return to Text -
Continued fractions were used in music theoretical writings of the 18th and 19th centuries Lambert (1774, 59) and Drobisch (1852, 76), see also Carey, N., & Clampitt, D. (1989, 197-198).
Return to Text -
See Barbour (1951), Žabka (2010; 2013), Muzzulini & Vogtenhuber (2016)
Return to Text -
Wardhaugh (2013, pp. 1-84), Descartes (1987, 47)
Return to Text -
I became aware of this diagram through a personal communication by Susan F. Weiss (1999). See also Snyder (1983, 1986).
Return to Text -
Gaukroger (1995, pp. 55-59). But Descartes did not treat meantone temperaments in his "Compendium musicae" or the tuning of lutes.
Return to Text -
The cent is a modern unit of interval size, so that the 12-edo semitone measures 100 cent and the octave therefore 1200 cent. To obtain cent values from Newton's values multiply his numbers by 100.
Return to Text -
There are 118 classes of chromatic scales that can be written as uninterrupted chains of Pythagorean fifths (3 : 2) and small fifths (40 : 27). See also Žabka (2013). The Pythagorean chromatic 12-note scale has just two different semitones (256 : 243 and 2187 : 2048). By convention, the note names of chromatic semitones begin with the same letter and differ by a simple alteration, such as C-C♯, D♭-D or F♯-F♯♯, whereas the notes E-F, C♯-D, C-Dd or F♯♯-G♯ form diatonic semitones. In syntonic chromatic scales the chromatic and/or diatonic semitones can occur in different varieties.
Return to Text -
See Barbour (1951), Muzzulini, D. & Vogtenhuber (2016)
Return to Text -
Frequency is measured in Hertz, i.e., full periods per second. Mark Lindley looked at Newton's octave divisions more than 30 years ago and claimed the Newton favored 53-EDO over all other divisions (Lindley 1987, pp. 206-210).
Return to Text -
The curves are explained in Wardhaugh (2013, 96-97).
Return to Text -
If they were the same, they would be equal to 6 semitones of the 12-tempered tuning.
Return to Text -
The distinction between deviations with respect to the unit and absolute deviations (in cent) is crucial for the notion of quality of best fit used in this article.
Return to Text -
See http://sound-colour-space.zhdk.ch/diagrams/39
Return to Text -
It is even optimal for EDOs with a unit interval greater than 0.67 cent. The coarsest better approximation is 1783-EDO, see Table 7.
Return to Text -
Later in this text the deviations are formally measured as root mean square deviations.
Return to Text -
According to Boethius, the interval of the Pythagorean comma is defined as six whole tones minus one octave. It has the ratio 531,441 : 524,228. Boethius (1867, 264-267: Inst. Mus. II, 31)
Return to Text -
Mercator's music theoretical manuscripts are published in Wardhaugh (2013, 129-236).
Return to Text -
Newton knew an interpretation of the Greek tetrachord's genera with syntonic intervals (Ptolemy, Zarlino) not looked at by Descartes.
Return to Text -
See Appendix_5 (http://hdl.handle.net/1811/92832) for detailed data about this point.
Return to Text -
Newton used the same abbreviations for the three semitones of his scale.
Return to Text -
If the condition 2c > a is violated, the lesser chromatic semitone is more like a quartertone than a semitone.
Return to Text -
Although 12-EDO does not distinguish between different semitones at all, it is a consistent approximation to Newton's syntonic chromatic scales.
Return to Text -
This is a general property for pairs of relatively prime numbers, so that even 612 could be obtained from 53 and 118 only:
Return to Text -
Notice that 306-EDO is related to 612-EDO as 59-EDO to 118-EDO. Both 306-EDO and 59-EDO give a "very poor" chromatic scale where some pitches are to be rounded by almost half an EDO unit. Newton did not give the full representation for 59-EDO, and he did not look at all at 306-EDO.
Return to Text -
The dimensions are given as side lengths of the cuboid not as numbers of grid points.
Return to Text -
The two graphs are differently scaled in the y-direction.
Return to Text -
Jacobus Leodiensis (ca. 1260 – after 1330), suggests and depicts a monochord with 53 micro-intervals per octave: 41 Pythagorean commas and 12 intervals a little smaller than the Pythagorean comma (Pythagorean semitones minus three Pythagorean commas), cf. Smits van Waesberghe (ed), (1988, p. 106, p. 139, f. 51r)
Return to Text
REFERENCES
- Barbour, J. M. (1951). Tuning and temperament. A historical survey. East Lansing: Michigan State College Press, Da Capo Press: New York 1972
- Barker, A. (1989 Ed.). Greek musical writings, Volume II Harmonic and Acoustic Theory, Cambridge: Cambridge University Press, 1989
- Barkowsky, J. (2007). Mathematische Quellen der musikalischen Akustik. Wilhelmshaven : Florian Noetzel Verlag
- Boethius, A. M. T. S. (1867). De institutione arithmetica libri duo: de institutione musica libri quinque. Ed. Godofredus Friedlein, Leipzig
- Bürgi, J. (1620). Aritmetische und geometrische Progreß-Tabulen, Prague 1620
- Carey, N., & Clampitt, D. (1989). Aspects of Well-Formed Scales. Music Theory Spectrum, 11(2), 187-206. https://doi.org/10.2307/745935
- Descartes, R. (1650). Renati Des-Cartes, Musicae Compendium. Strassbourg: Heitz
- Descartes, R. (1987), Abrégé de musique. Compendium musicae. Traduit et introduit par Frédéric de Buzon Paris : Presses Universitaires de France
- Drobisch, M. W. (1852). Über musikalische Tonbestimmung und Temperatur, Leipzig. Weidmannsche Buchhandlung
- Euler, Leonhard. (1739). Tentamen novae theoriae musicae. St. Petersburg
- Fludd, R. (1618/24). Utriusque cosmi historia, Vol I, Tract II, Part II, Lib. I, 1624 (first edition 1618)
- Fogliano, L. (1529). Musica theorica. Venice: Io. Antonius et Fratres de Sabio, 1529
- Galilei, V. (1581). Dialogo di Vincentio Galilei … della musica antica, et della moderna. Firenze
- Gaukroger, S. (1995). Descartes: An Intellectual Biography. Oxford: Clarendon Press.
- Hall, D. (1973). The Objective Measurement of Goodness-of-Fit for Tunings and Temperaments. In: Journal of Music Theory, Vol. 17, No. 2, pp. 274-290. https://doi.org/10.2307/843344
- Holder, W. (1731). A treatise of the natural grounds, and principles, of harmony. London 1731 (first edition 1694)
- Huygens, C. (c. 1661). Divisio octavae in 31 intervalla aequalia. In: Oeuvres complètes de Christiaan Huygens, Tome 20, La Haye: Martinus Nijhoff 1940, 147-149
- Jacobus Leodiensis, (s.a.) Compendium De Musica, Bruxelles, Bibliothèque Royale 10162-66. In: Ed. Smits van Waesberghe, J. et al. (1988). Jacobi Leodiensis – Tractatus De Consonantiis, Tractatus de Intonatione Tonorum, Compendium de Musica. Buren: Frits Knuf, 88-122, Facs. : 133-146
- Jedrzejewski, F. (2018) Quirinus van Blankenburg's Transporteur. Journal of Mathematics and Music, 12:2, 123-124. https://doi.org/10.1080/17459737.2018.1478649
- Kepler, J. (1619). Ioannis Keppleri Harmonices mundi libri V. Lincii, Austriae 1619. Lib III. https://doi.org/10.5479/sil.135810.39088002800316
- Kircher, A. (1650). Musurgia Universalis. Rome: Ludovico Grignani
- Mersenne, M. (1636). Harmonie Universelle, contenant la Theorie et la Pratique de la Musique. Livre Second, Des Dissonances. Paris
- Lambert, J.-H. (1774). Remarques sur le tempérament en Musique. In Mémoires de l'Académie de Berlin, 1774, 55-73
- Lindley, M. (1987). Stimmung und Temperatur. In: Hören, Messen und Rechnen in der frühen Neuzeit, Geschichte der Musiktheorie Bd. 6, 109-331. Darmstadt: Wissenschaftliche Buchgesellschaft
- Mercator, N. (s.a.). Musical Notebook / Theoria Musices / Of Musick (1) / Of Musick (2). In: Wardhaugh (2013, pp 129-236)
- Muzzulini, D. (2015). The geometry of musical logarithms. Acta Musicologica LXXXVII/2, 193–216
- Muzzulini, D. (Ed. 2023). Sound Colour Space – The Art of Diagram. ZHdK (in prep.)
- Muzzulini, D. & Vogtenhuber R. (2016). Chromatic Scales. Retrieved from http://sound-colour-space.zhdk.ch/exhibition/chromatic-scales
- Newton, I. (1665). Of Musick. In College Notebook. MS Add. 4000, f. 138r-f. 143r. Cambridge University Library. Retrieved from http://cudl.lib.cam.ac.uk/view/MS-ADD-04000. All pictures from MS Add. 4000 are reproduced by kind permission of the Syndics of Cambridge University Library. Critically edited in: Wardhaugh (2013, pp. 85-113).
- Newton, I. (1704). Opticks: Or, a Treatise of the Reflexions, Refractions, Inflexions and Colours of Light. London. https://doi.org/10.5479/sil.302475.39088000644674
- Rameau, J.-P. (1726). Table des Progressions. Nouveau système de musique thèorique. Paris 1726, 24
- Salinas, F. (1577). De musica libri septem. Mathias Gastius, Salamanca, 1577
- Schechter, M. (1980). Tempered Scales and Continued Fractions. In: The American Mathematical Monthly, Vol. 87, No. 1, 40–42. https://doi.org/10.1080/00029890.1980.11994951
- Snyder, J. L (1983). Theinred of Dover on Consonance: A Chapter in the History of Harmony. In: Music Theory Spectrum 5, pp. 110-120. https://doi.org/10.2307/746098
- Snyder, J. L. (1986). Non-Diatonic Tones in Plainsong : Theinred of Dover versus Guido d'Arezzo. In : La musique et le rite sacré et profane. Strasbourg Vol. II pp. 49-67
- Stevin, S. (c. 1605). Van de Spiegheling der Singconst (ms). "Van de Spiegeling der Singconst" et "Van de Molens" : Deux traités inédits, Bierens de Haan, 1884
- von Oettingen, A. (1917). Die Grundlagen der Musikwissenschaft und das duale Reininstrument. Leipzig. Hirzel, 1917
- Waldvogel, J. (2014). Jost Bürgi and the discovery of the logarithms. In: Elemente der Mathematik, Volume 69.3, 89–117. https://doi.org/10.4171/EM/253
- Wardhaugh, B. (2013 Ed.). The Compendium Musicæ of René Descartes: Early English Responses. Musical Treatises. Turnhout: Brepols
- Žabka, M. (2010). Well-formedness in two dimensions: a generalization of Carey and Clampitt's theorem. Journal of Mathematics and Music, Volume 4.1, 2010 - Issue 1. https://doi.org/10.1080/17459737.2010.491975
- Žabka M. (2013). The Minkowski Geometry of Numbers Applied to the Theory of Tone Systems. In: Yust J., Wild J., Burgoyne J.A. (eds) Mathematics and Computation in Music. MCM 2013. Lecture Notes in Computer Science, vol 7937. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-39357-0_18
- Zarlino, G. (1562). Le istitutioni harmoniche. Venetia 1562 (first edition 1558)
- Zarlino, G. (1588). Sopplimenti musicali. Venetia: Francesco de Franceschi, Sanese