EARLY recordings tend to receive scholarly attention when they violate the norms of late 20th- and early 21st-century performance practice. Philip (1992, 2004) describes such vagaries as extreme agogic accents, unmarked tempo changes, rubato and portamento. Focusing on piano music, Peres da Costa (2012) adds asynchrony of hands and unnotated arpeggiations. Focusing on performers' deviations from modern standards shows only part of the difference between early-recorded and modern practice. The more subtle fundamentals of musical performance change too: disposition of accents, proportioning of beats within the measure, treatment of cadences, conception and execution of grouping structure. The following case study of timing in performances of Chopin's Etude in A flat Major, Op. 25 no. 1, aims to show how foundational rules of phrasing and expressive nuance have changed over the history of recorded music.
Repp's (1992, 1998) studies of recordings of Schumann's Träumerei and Chopin's Etude Op. 10 no. 3 are early models for the current study. Both focus on discovering norms of expressive performance rather than historical change. Repp (1998) examines a broad range of recorded performances of a Chopin etude, but the analysis is limited to the first five measures, and the focus is on the micro-level of rhythm.
Studies that describe how music performance has changed over time include Leech-Wilkinson (2015) and Cook (2007), both of which theorize shocking chasms between early recorded performances and present convention. In the present study I aim to supplement their research by investigating the substrata of those styles. Technology limits Katz (2003) and Bowen (1996) to discussion of large-scale timing issues. In her study of recorded performances of Bach's violin partitas, Fabian (2017) shows that, "far from being neat categories, performing styles and precepts are constantly shifting, largely imperceptibly." (p. 0.3) Chopin's Etude, Op. 25 no. 1, is an ideal locus for studying those deep-seated and subtle changes in style, as its limited materials largely prevent the signaling of stylistic categories such as Fabian's (2017, 2.1) "vitalist or Romantic-modernist (RMP), the literalist or Classical-modernist (CMP), and the historically informed performance (HIP) styles."
Cook's (1995) and Dodson's (2002, 2008, 2011a, 2011b) work shows the interactions between performance decisions and certain methodologies of music theory, most notably Schenkerian analysis. Rink (2001, 2015) and Rink, Spiro and Gold (2011) argue for a plural conception of musical structures communicated through performance. Rink (2001), Barolsky (2007) and Dodson (2011b) demonstrate how various performances embody certain analytical perspectives. In similar fashion, Ohriner (2012) argues that grouping structure is not necessarily immanent in the composition; rather, performers use timing to create grouping structures. Spiro, Gold and Rink (2010) used a bottom-up approach to examine patterns of beat timings in Chopin's Mazurka op. 24 no. 2. Although not an evaluation of changing practice, their study illustrates the difficulty mapping structural features onto performance decisions, on a one-to-one basis, in a piece that varies along so many musical parameters. The present study attempts to stake out a middle ground between theory-first structuralism and the inductive approach to performance analysis advocated by Cook (2013, p. 55). Discussion of compositional features below is limited to concepts readily understandable to performers: grouping structure and cadences, harmony and dissonance.
Bach's Prelude in C Major, from the Well-Tempered Clavier Book 1, has been used in case studies of timing strategies because of its limited materials (Cook 1987, Benadon and Zanette 2015). Chopin's Etude, Op. 25 no. 1, shares that piece's uniformity of texture, with the added element of a prominent melody line. Timmers, Ashley, Desain and Heijink (2000), noting shortcomings in generative models of expressive timing, ran an experiment showing how tempo rubato changes in different textural contexts. The consistency of textural context in the etude not only makes it possible to map timing strategies onto musical parameters, but also allows the ways in which pianists treat musical events across the entire etude to be compared meaningfully.
Although it can be dangerous to rely on a single musical parameter when describing performance practice, Chopin's Etude, Op. 25 no. 1, offers several advantages. Large numbers of recordings from all historical periods allow for robust statistical analyses. More importantly, the piece's consistent texture controls for many potentially disruptive variables. The role of articulation is minimized by the universally pedaled sonority. The unvaried quarter notes of its melody do not allow for rubato based on long and short note-values. The constant stream of accompanying sextuplets resists dramatic tempo changes and abrupt agogic accents; extreme slowing loses the "Aeolian harp" quality of sound; and extreme speed is limited by technical difficulty. The piece is long enough to provide a rich context and points of comparison for performers' decisions. Pedaling, articulation, asynchrony of hands, smoothness of the figuration, dynamic balancing of parts and the other subtleties of craft play their part, but overall the pianist's range of interpretive strategies is severely limited. Performances of the etude show far less striking change over the history of recorded music than most of Chopin's works. Except for surface noise and tonal quality, early recordings do not display obvious markers of their age, even though many are of pianists frequently cited as exemplars of a playing style that predates recording technology. Fabian (2008) argues that "the epistemological and ontological differences between live performances and recordings may be less important to performance practice researchers than theorists and philosophers posit." (p. 252) The lack of idiosyncrasy in the early performances of the etude creates an opportunity to witness deeper and more subtle changes in performance practice, both recorded and unrecorded.
METHOD
This study is based on a broad collection of recordings—127 in total, including most of the commercial recordings made before 1950. Most of the recordings were either digital to begin with or converted professionally. Some long-playing vinyl records (33 ⅓ rpm) were converted by connecting the record player's headphones output jack directly to a computer via an audio cable and recording the music using Audacity. Positions of right-hand melody note attacks were recorded using Sonic Visualiser, first by tapping along the with the music at normal speed, quarter-note pulse, then adjusting the markers while listening again at 20% playback speed and looking at the spectrogram. Final checks were then performed while listening at full speed. The melody notes are extremely clear, even in the lowest-quality recordings.
RESULTS AND DISCUSSION
Empirical analysis of timing in recordings shows that performances of this etude slowed down over the last one hundred years. Overall, the data do not show an increase or decrease over time in the amount of tempo fluctuation. 2 Independently of a tendency to use slower tempi, pianists changed the way they employ rubato. 3 Several factors contribute to the tendency towards lengthening the fourth beat at the expense of the second and third: an increase in phrase-final lengthening, an increase in the use of tempo arching for shorter groups of measures, and a tendency to delay the arrival of an accented dissonance or change of harmony instead of lengthening the melody inter-onset interval (hereafter IOI) of the event itself. 4 Illustration of trends in performance across the entire 20th and into the 21st century shows how interpretation changes slowly in aggregate, even imperceptibly. The data call our attention to the continuum of possibilities between early recorded styles and the conventions of modern players and suggest that some practices thought to be the bedrock of expressive performance may be historically conditioned.
Melody IOIs describe the duration between the timing instants marked by the tapping procedure. For example, the melody IOI of m. 1.1 (measure 1, beat 1) describes the duration between taps on m. 1.1 and m 1.2. Tapping data were converted into tempo measurements using the IOI of each melody note with the melody note preceding it. Discussion below of global measures of tempo fluctuation, phrase-final lengthening, and tempo arching is based on tempo data. The sections on metrical patterning and agogic accents use duration of melody IOI. To calculate median and standard deviation of tempo, the last four beats (m. 48.2 to 49.1) were omitted; they do not continue the texture of the etude.
Based on correlations between musicians' timing profiles in performances of the same piece from different stages of their careers, Leech-Wilkinson (2009) asserts that musicians tend to learn their style at an early age and that it generally persists throughout their careers. This suggests that any statistical analysis of style change over time would better employ the performer's year of birth than the year of the recording. In general, data from the present study support Leech-Wilkinson's assertion. Correlations based on year of performance will only be reported in the rare instances where they are stronger than those based on the performers' year of birth; year of birth usually provides a stronger correlation (r) with the variables of interest and lower p value. Variables used in correlations and residuals from regression analysis were checked for normality using the Shapiro-Wilk test. All were determined to be normal except for those noted below.
The most basic change in performance practice for Chopin's Etude, Op. 25 no. 1, over time is a slowing of tempo. 5 Both performer's year of birth and year of performance weakly predict slower median tempo; unusually, year of performance, r (125) = -.26, p = .004, shows a stronger relationship than year of birth, r (125) = -.22, p = .013. Chopin's metronome mark is quarter note = 104. Only 14% of performers realized a median tempo of at least that mark; the rate for pre-1950 recordings was 25%. The performer's age was not correlated with their tempo choice. Two caveats to this tempo trend should be noted: both the technologies involved in making early recordings and the process of digitizing records introduce variability in tempo and pitch; for a full discussion of these issues see Leech-Wilkinson (2009). Many of the recordings on 78 rpm records were paired with another short piece. The time limit of these discs (about three minutes for a 10-inch disc, and five minutes for a 12-inch disc) could have induced some pianists to play faster than they would have in concert. Because the present study is based on proportional measurements, these issues with early recordings have minimal or no impact.
Global Measures of Tempo Fluctuation
Popular discussions of recorded piano playing (e.g. Dubal, 2004, p. 10) usually argue that performances from the first half of the 20th century are rhythmically freer than those from the second half. Peres da Costa (2012) makes the following statement:
For the uninitiated, [early] recordings give the general impression of exaggerated temporal waywardness. Yet many important pianists of the era evidently considered such a style to be highly expressive. In contrast, most pianists today adhere more faithfully to the dictates of notation: any modification tends to stay within close proximity of the prevailing tempo. (p. 252)
The present analysis of recorded performances of Chopin's Etude, Op. 25 no. 1, tells a different story. Global measures of tempo fluctuation show no historical trends, increasing or decreasing. The coefficient of variation—i.e. standard deviation of melody IOI divided by average melody IOI—for each performance describes both onset-to-onset changes and changes of tempo between larger sections. 6 If a performer plays a section faster or slower than the prevailing tempo, standard deviation could be high without the local push and pull of rubato. To measure timing deviations between successive melody IOIs, the absolute value of the difference between successive melody IOIs was calculated. These values were then averaged and divided by average melody IOI. Data for both global measures of timing fluctuation are shown in Figure 1, with labels for some of the extreme values. Note the wide range of values for both measures across all time periods and the lack of an overall trend in the data.
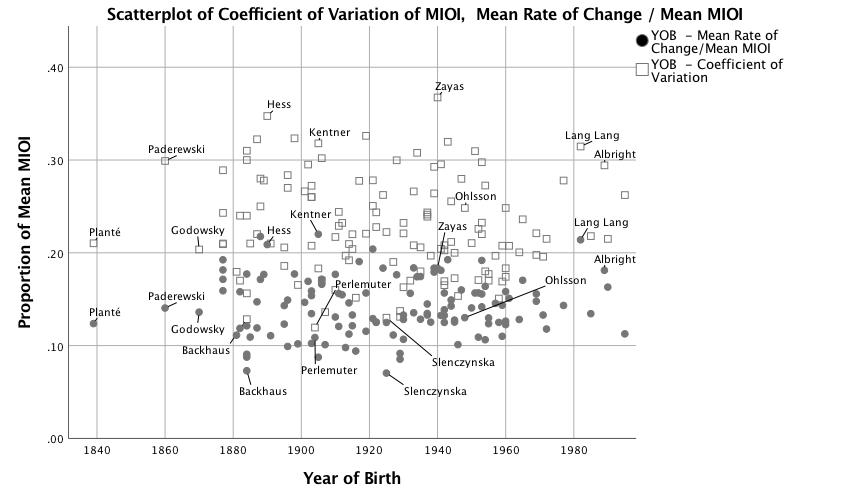
Figure 1. Scatterplot of standard deviation melody IOI divided by mean MIOI and mean rate of change between MIOI divided by mean MIOI vs. pianists' year of birth.
Slower performances display a higher absolute quantity, but not a higher relative quantity, of tempo fluctuation. As median tempo increases, we can observe decreases in standard deviation of melody IOIs, r (125) =-.37, p < .001), and onset-to-onset change of melody IOIs, r (125) = -.38, p < .001. Correlations of median tempo with the coefficient of variation and with mean rate of change between MIOI divided by mean MIOI are not significant, p > .05. The role of tempo in the broad changes in expressive timing strategies discussed below is much smaller than the role of the performer's year of birth.
Phrase-Final Lengthening
One of the foundational elements of generative approaches to expressive performance is the concept of phrase-final lengthening—a musical parallel to the widely-observed tendency in human speech of slowing down at the end of a phrase. Todd (1989) states that the degree of slowing is a function of the importance of the boundary. In his description of iconic signification (following Peirce), Clarke (1995) makes the following claim: "A large-scale sectional break will typically be approached with a greater degree of slowing than a small-scale group boundary, an effect which can be heard particularly in performances of nineteenth-century piano music (such as Chopin)." (p. 27) On the large scale, pianists' timing shapes in recorded performances of Chopin's Etude, Op. 25 no. 1, are fairly consistent. Each line in Figure 2 shows the average tempo at each beat of performances grouped by performer's year of birth in 20-year increments; error bars represent the standard error of the mean of each group of performers at each point in time. These average timing profiles display a series of arches that usually correspond to the pianists' interpretations of grouping structure.
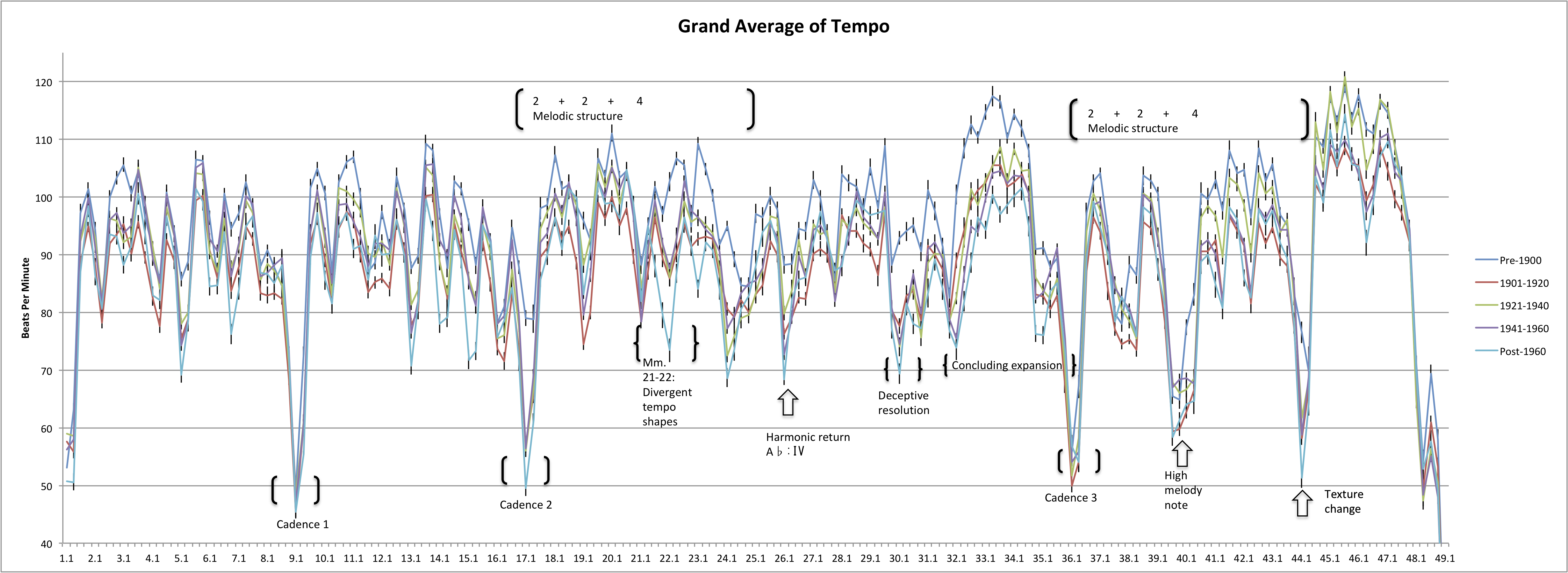
Figure 2. Line graph showing average tempo at each beat of the etude. Error bars represent standard error. Pianists are grouped by year of birth in 20-year increments.
A brief analytical discussion of Chopin's Etude, Op. 25 no. 1, is necessary to compare the pianists' performed timing interpretations with the composed phrases. The piece begins with two eight-measure phrases ending in cadences. The section starting at m. 17 is more complicated. Melodically, the grouping structure of mm. 17-24 is 2+2+4, and the composer provides a ritenuto with dashes throughout m. 24. The bass line (^3-^4-^5-^1) and harmony in mm. 21-22 suggests a five-measure unit from mm. 17-22 that completes a harmonic sequence of ascending thirds. Modal mixture intensifies the sense of arrival at m. 22. M. 25 functions as an anacrusis to the sub-phrase beginning in m. 26. This four-measure unit ends with a deceptive resolution, then is repeated with a "concluding expansion" (Burkhart, 1997) in mm. 32-34 before the final cadence in m. 36.
The timing profiles in Figure 2 conform to the composed phrase lengths in mm. 1-16. In the section from mm. 17-36, the average obscures multiple distinct timing interpretations—some privileging certain harmonic events, others focusing on melodic repetition. 7 The ambiguity in grouping structure in this passage leads to a wide variety of possibilities for phrasing demonstrated in performance. A steep phrase-final lengthening occurs next at m. 36. The timing graphs for the post-cadential extension at mm. 36-44 resemble a phrase; note that the dip at 39.3-4 coincides with the high melody note rather than the start of a four-measure group in m. 40.
Phrase-final lengthening is the difference between the prevailing tempo and final tempo of a phrase. Larger ritardandi, which sound like deviations from the prevailing tempo, will have less effect on median than average tempo, so the median is a better measure of prevailing tempo. For measuring final tempo, the first two phrases and the climactic phrase ending in m. 36 are unproblematic. In the middle section, most pianists reach a low ebb of tempo in m. 24 or on the downbeat of m. 25. That low point marks the measurement of final tempo for the unit at mm. 17-25. Mm. 36-44 represent a post-cadential tonic expansion. Because of the 2+2+4 melodic structure and the texture change in m. 44, pianists tend to treat this passage as if it were a phrase by lengthening its ending. To compare performances meaningfully, the difference between final tempo and prevailing tempo must be expressed as a proportion. Final lengthening proportion in the following discussion is calculated as the difference between final and prevailing tempo divided by prevailing tempo.
Most performances of segments of the etude show consistent amounts of final lengthening that do not change much over time. Table 1 shows the mean final lengthening proportion for passages where lengthening is not significantly correlated with performer's year of birth. 8
| Mm. 1-8 | Mm. 17-25 | Mm. 25-36 | Mm. 36-44 | |
|---|---|---|---|---|
| Mean Phrase-Final Lengthening Percentage | .35 | .28 | .71 | .30 |
Figure 3 shows a significant trend over time whereby the final lengthening of the phrase from mm. 9-16, R2 = .16, F(1,125) = 27.23, p < .001, as well as a wider variety of timing decisions among earlier pianists. Final lengthening in m. 16 increases, year-by-year (the later the pianist's year of birth, the greater the proportional slowing), by .3% (β = .42, p < .001). This passage—and the section from mm. 36-44 where increases in final lengthening over time barely missed statistical significance—features a harmony that continues into the next group. Instead of a change of chord at the sectional boundary, the C major chord in m. 16 becomes a C 6/5 in m. 17 and the A-flat major chord from m. 43 continues into m. 44, although the melody is replaced by decorative arpeggios. The early performance practice of continuing the same tempo or accelerating over these boundaries has disappeared from more recent performances.
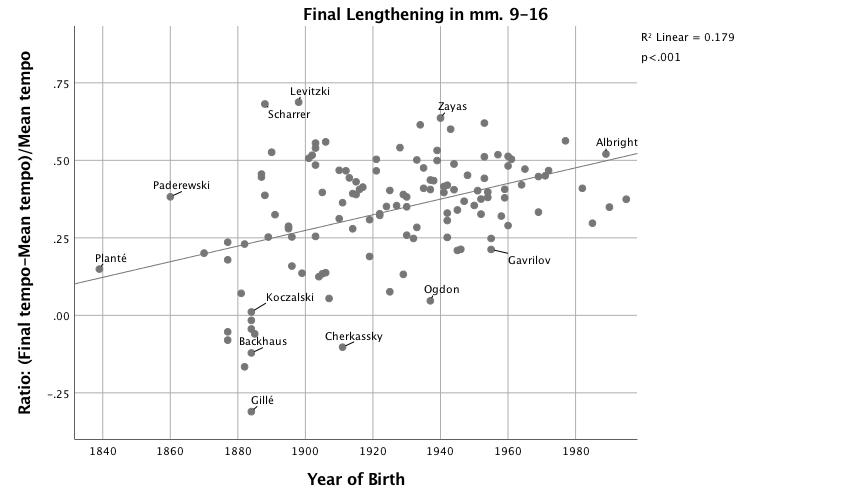
Figure 3. Scatterplot with linear fit line of proportion of phrase-final lengthening in mm. 9-16 vs. year of birth.
In contrast to the more consistent practice of final lengthening in modern performances, early-recorded pianists use a wide variety of strategies in the transition from m. 16 to m. 17. 9 Some change almost always occurs on the downbeat of m. 17 that clarifies the beginning of a new phrase. Among the performers who choose not to slow down in m. 16, Backhaus (1909, b.1884) makes a dynamic accent and plays in a faster tempo. Planté (1928, b.1839) makes a dramatic change of color by suddenly playing softly and clearing the sustained, pedaled sound abruptly. Koczalski (1938, b.1884) uses dynamic accents, slight desynchronization of the hands and clever pedaling—engaging the right pedal slightly late—to create short articulations in the bass voice at m. 17. The three recordings of this passage can be heard in Audio Example 1. 10 Notably, the two most extreme ritardandi in m. 16 can be found in some of the oldest recordings, for example those of Scharrer (1912, b.1888) and Levitski (1923, b.1898). A few early recordings eschew both approaches; they lack the crafty execution of Backhaus, Planté or Koczalski as well as phrase-final lengthening in m. 16. Nevertheless, the assumption that the communication of grouping structure depends on final lengthening is clearly incorrect in this instance.
The documentary evidence for phrase-final lengthening is mixed. Brown (1999) quotes Crelle's treatise of 1823: "as a rule, the beginning of a musical unit commences powerfully and importantly, the middle carries on in a measured and regular manner and the end increases in speed and decreases in power." (p. 385-386) A decade later, Kalkbrenner advises that "all terminations of cantabile phrases should be retarded." (qtd., in Brown 1999, p. 386) Performance theorists in the end of the 19th century such as Christiani (1885) and Riemann (1888/1892) were intensely interested in grouping structure. 11 Recordings of Chopin's Etude, Op. 25 no. 1, suggest that early-recorded pianists shared that interest, although the means of expressing their interpretation was dependent on context and highly individualized. Slåttebrekk and Harrison (2010) observed something similar in their project recreating the recordings Grieg made in Paris in 1903: "Grieg seems constantly to avoid any obvious combination of strategies at phrase endings or transitions. A combination of, for example, relaxation, diminution, and retardation with a clear-cut, prepared turning point of the phrase is virtually non-existent in his performances." In his analysis of Schenker's performance commentary on Schubert's Impromptu, Op. 90 no. 3, Cook (2013) writes "although Schenker refers to 'the usual ritardando' it appears that he means not that this cadence [m. 109] should be treated as an exception, but that 'the usual' way of playing is wrong." (p. 72) He then quotes Schenker from 1911: "the requirement that a composition's form not be exposed too nakedly frequently demands considerably quicker playing where the seam occurs." For pianists born before about 1930 it was possible to play the phrase in Chopin's Etude, Op. 25 no. 1, that ends at m. 16, and the section break at m. 44, with little or no ritardando, indeed even with accelerando; more recent performers play as though the ritardando were mandatory.
Tempo Arching
Tempo arching—a slow beginning, followed by accelerando and final lengthening—has been part of the performance practice of the etude since the earliest recordings. Later in the 20th century it became a primary means of delineating grouping structure. Studies such as those by Todd (1985), Repp (1997) and Windsor and Clarke (1997) model tempo arches, viewing the expressive execution of the music as historically static. Close examination of recordings of the etude suggests differences between historically conditioned norms and more absolute rules, at least as regards the last 100 years or so, and possibly earlier. 12
The following discussion is indebted to Cook's (2013, pp. 176-223) important account of the rise of phrase arching in the post-war period. Cook compared performances to an integrated model of hierarchically-nested tempo and dynamic arches. This model is based on Todd's (1992) theory of expression. Instead of reducing a performance to a single measurement (even a highly descriptive one, as in Cook's study), the present study describes the timing only of specific passages and how pianists' readings of them have changed over time. Note that this analysis does not attempt to find a curve of best fit for each segment of each performance, but rather to determine the presence or absence of an arch in a particular segment of music.
First, sections where the pianists employed tempo arching were identified, limiting the passages investigated to those starting and ending on the first beat of a measure and respecting the most obvious elements of Chopin's grouping structure. Pearson product-moment coefficients (r-values) were then calculated for the correlation between tempo and a quadratic function with negative sign, having x-intercepts at the origin and the value corresponding to the length of the musical segment. A quadratic function has been used in previous research (Todd, 1985; Cook, 2013) because it describes physical phenomena such as the path of a thrown object. In this case, r represents the smoothness or predictability of a certain tempo arch in a given performance; the "height" of the pianists' tempo arch has no impact on the correlation. Pianists' tempo shapes were compared with prototype arches rather than fitting the curve to each particular performance for several reasons. 13 The sign of the curve should be negative because tempo arches do not start fast and climax slowly. To prevent a regression that fits only one side of the arch, the curve must contain an inflection point. To avoid confusing a six-measure segment of an eight-measure arch with a true eight-measure arch, for example, the inflection point should come at the middle of the musical segment. Therefore, this analysis does not describe how closely quadratic arches model actual performances—interpreted aurally, perhaps, as overall smoothness—but whether a symmetrical arch that starts and ends slowly is present in a given segment of a performance.
The threshold for counting a segment as an arch was set at r = .60. Foundational research on the validity of this measure in the broader population has yet to be conducted. Video Example 1 shows tempo data plotted against the prototype arch for an eight-measure segment (mm. 1-8) performed by three pianists: Wild (1947, b.1915) at r = .54, Ohlssohn (1998, b.1948) at r = .63, and Rubinstein (1964, b.1887) at r = .70. The same trends shown on Figures 4-7 for r > .60 can be observed in the data using r = .70 as a threshold, indicating that the number of two- and four-measure arches had doubled in performances by pianists born in 2000 compared with performances by pianists born in 1880.
Figures 4-7 show the number of segments of a given length for which correlation with the prototype arch produces r > .60, plotted against the pianist's year of birth. Residuals from the regression analyses of numbers of arches are significantly non-normal. This is most likely caused by a threshold measurement (r > .60) to count the presence of an arch; a segment where r = .59 will not be counted while a segment of r = .60 will, although they are very similar. The statistical models are nevertheless robust; large sample size and low p values mitigate this violation of the assumptions of regression analysis. Figure 4 shows that the most dramatic increase of tempo arching over time is in groupings of two-measure units, R2 = .17, F(1,125) = 25.46, p < .001. Four-measure units also increase significantly over time (see Figure 5), but the effect size is smaller, R2 = .05, F(1,125) = 7.20, p < .01. Figure 6, for eight-measure arches, has no trend line because the change over time is not significant. Irregular groupings—three-, five-, six- and seven-measure segments—are charted together in Figure 7 because each type is uncommon; together they show a significant increase over time, R2 = .06, F(1,125) = 7.21, p < .01. Clarke (1985) suggests that "at slower tempi, the upper limit of the perceptual present puts a constraint on overall group size and requires a performer to subdivide large groups and to establish the boundaries of smaller groups more convincingly" (p. 217); see also Clarke (1982). Both year of birth and median tempo predict the number of two-measure arches in a performance, Adj. R2 = .20, F(2,124) = 15.16, p < .001, but performer's year of birth (β = .37, p < .001) is a much stronger predictor than tempo (β = -.17, p = .04). 14 Median tempo is not correlated with the number of any other length arches. A negative correlation between median tempo and number of eight-measure arches was found to be marginally significant: r(125) = -.17, p = .051.
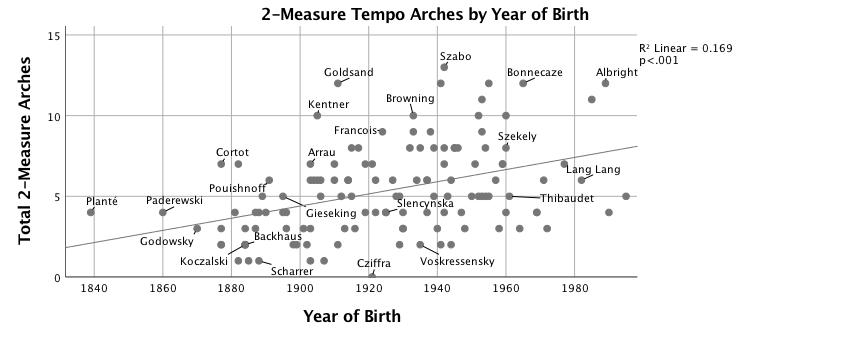
Figure 4. Scatterplot with linear fit line of number of two-measure tempo arches correlated (r > .6) with quadratic model vs. year of birth.
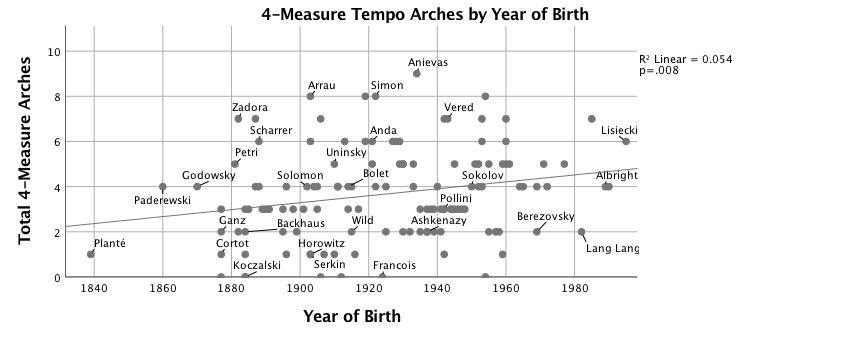
Figure 5. Scatterplot with linear fit line of number of four-measure tempo arches correlated (r > .6) with quadratic model vs. year of birth.
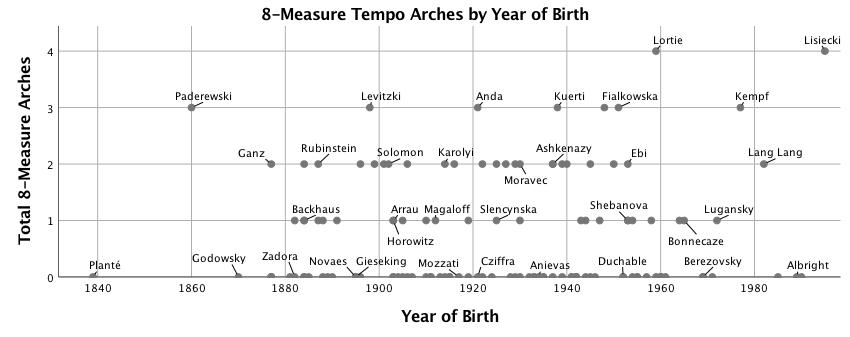
Figure 6. Scatterplot with linear fit line of number of eight-measure tempo arches correlated (r > .6) with quadratic model vs. year of birth.
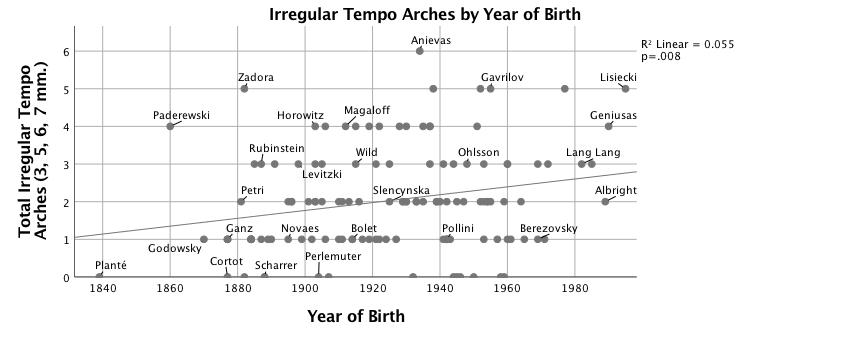
Figure 7. Scatterplot with linear fit line of number of three-, five-, six- and seven-measure tempo arches correlated (r > .60) with quadratic model vs. year of birth.
Comparing tempo in discrete segments of music with arches shows that the way pianists realize certain compositional elements in the score has changed over time. Smoother arches, described by higher r-values, are characterized by predictable speeding-up at the beginning, slowing at the end, and a lack of agogic accentuation in the middle of the arch. They often give a strong sense of the pianist's interpretation of grouping structure. The tempo shape of almost every segment of the etude is becoming, on average, more arch-like over time. Dramatic increases in arching can be observed in the two-measure arches starting in mm. 3, 11, 26, 28 and 30, perhaps responding to two-measure melodic units and their repetitions. Some of the most significant increases seem to be driven by slowing in cadential progressions: the five-measure arch from mm. 17-22, the four-measure arch from mm. 32-36, and the two-measure arch at mm. 15-16. Pianists increasingly bind m. 21 to m. 20; Figure 8 shows the Pearson correlation (r) between pianists' tempo in a five-measure arch beginning in m. 17 with their year of birth.
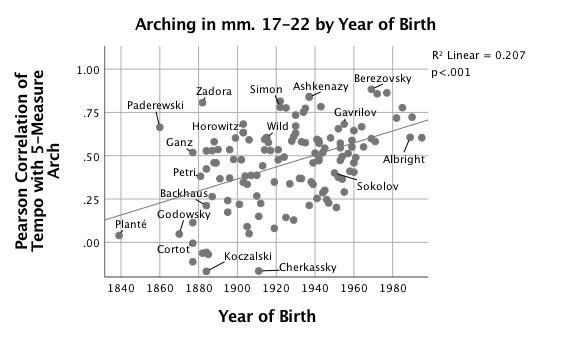
Figure 8. Scatterplot with linear fit line of correlation (r) of tempo in mm. 17-22 with 5-bar arch vs. year of birth.
Note the wider variety of values among earlier performers. There is a significant trend such that smooth tempo arches can be found in more recent recordings of this passage, R2 = .21, F(1,125) = 32.68, p < .001. Performer's year of birth is also correlated with a three-measure arch beginning in m. 19, r (125) = .37, p < .001. The stronger correlations between pianists' timing shapes and quadratic arches in more recent performances reflect the growing tendency to mark the cadence in m. 16 and the V7-I (with modal mixture) in m. 22 with slowing, as well as a generally smoother, less agogically-marked style of playing.
Tempo arching was an interpretive possibility throughout the recorded history of Chopin's Etude, Op. 25 no. 1. Nearly all the tempo arches that occur in the later 20th century can be found in the early recordings as well, although two-measure units—especially in mm. 1-16—are extremely rare. The Polish-American pianist and Busoni pupil Michael Zadora (1922, b.1882) seems to use tempo arching as a guiding principle of his interpretation. Zadora plays six four-measure arches (r > .6), a surprising number of arches for a musician born in 1882 (see Audio Example 2). Where he might have learned it is unclear. The recording made by his contemporary and fellow Busoni pupil Egon Petri (1951, b.1881) shows much less arching. Zadora and Paderewski (1912, b.1860) both play a five-measure arch from mm. 17-22, which, according to Figure 7, is a modern idea. The three-measure arch from 19-22 can be found in the recording by Broman (1919, b.1887). The six-measure arch from mm. 30-36, always a popular practice, has among its earliest exponents Godowsky (1924, b.1870), Ganz (1919, b.1877) and Cortot (1925, b.1877). A seven-measure arch from 25-32 appears first in Petri's recording (1951, b.1881). Eight-measure arching (mm. 1-8, 9-16, 17-24) goes all the way back to Paderewski's performance. In his study of phrase arching in Chopin's Mazurka, Op. 63 no. 3, Cook (2013) writes that "the development of a new approach to phrase arching did not extinguish previous performance options." (p. 206) The number of possible interpretations expanded "during the period up to the 1950s." In the analysis of the present etude, the data for individual phrasing decisions sometimes show a shift either from an eight-measure arch towards two-measure arches in mm. 1-8, or from an eight-measure arch towards a 2+2+4 arching structure in mm.36-44. In other passages the data show the field of interpretive possibilities narrowing, as a smooth four-measure arch in mm. 32-36 or a five-measure arch in mm. 17-22 becomes more common.
Cook (2009) describes a dichotomy between "rhetorical" and "structuralist" performance styles, and tempo arching data for Chopin's Etude, Op. 25 no. 1, do suggest that structuralist performances are increasingly ascendant. However, as shown above in the discussion of early practices of phrase-final lengthening in mm. 16-17, the quantitative data need a rich context to be understood. Backhaus, Planté and Koczalski clearly mark the phrase boundary in m. 17, but not by using tempo. Figure 9 shows arching according to performer's year of birth in another such passage: mm. 32-36; pianists' tempo curves in this section have become significantly more arch-shaped over time, R2 = .09, F(1,125) = 11.78, p < .01.
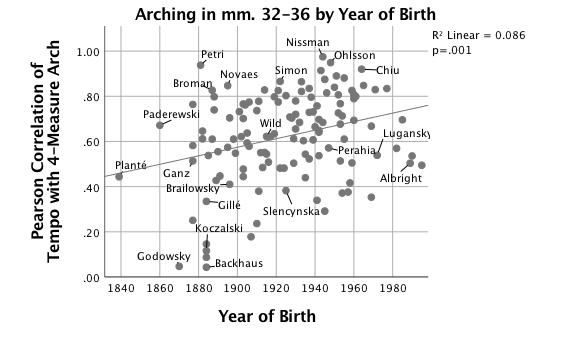
Figure 9. Scatterplot with linear fit line of correlation (r) of tempo in mm. 32-36 with 4-bar arch vs. year of birth.
With outliers excluded (un-arched performances by Godowsky and Backhaus) this trend is still significant, R2 = .05, F(1,122) = 6.11, p = .02. Arching has become more consistent over time, and tempo shapes showing very low correlation with an arch (either flat or marked agogically) have disappeared from recent performances. Irrespective of historical period, pianists' tempo curves in this section—from the start of a phrase expansion leading to final confirmation of the tonic key—are among the most consistently arch-shaped segments of the etude. Phrase-final lengthening in m. 36 is unsurprisingly common to almost all performances, accounting for a significant portion of the correlation. Multiple late-19th-century sources prescribe a tempo arch for such an arch-shaped melody. 15 However the earliest performers are the least likely to heed this advice. Koczalski (1938, b.1884), Planté (1928, b.1839), Backhaus (1909, 1928, 1951, b.1884) and Gillé (1950, b.1884) all clearly mark the start of the expansion with a faster tempo, then either play in a sharply rhetorical way with less predictable rubato or use a four-measure ritardando. Audio Example 3 consists of recordings of performances by Planté, Backhaus (1928) and Gillé. The faster tempo at m. 32 is a common idea; 83 of the 127 performances increase the tempo by at least 5%. Some early-recorded pianists, such as Broman (1919, b.1887), Novaes (1958, b.1895), Petri (1951, b.1881) and Scharrer (1912, b.1888), create very smooth tempo arches in mm. 32-36. Audio Example 4 contains mm. 30-36 played by Petri (r = .94 for arching in mm. 32-36), Broman (r = .83), and Novaes (r = .85). The pianists who create a tempo arch and those who do not both seem equally aware of m. 32's status as a deviation from the expected grouping structure. Some pianists born after 1980 have shied away from the smooth arch. This may represent a backlash against the style of the previous generation.
A pianist's use of a tempo arch does not necessarily represent an interpretation of grouping structure. In the examples of mm. 32-36 provided above, early-recorded pianists often communicate grouping ideas without using tempo arches. Likewise, a clear tempo arch does not necessarily indicate an interpretation of phrase structure. Scharrer (1912, b.1888), for example, creates an arch in mm. 2-3 (Audio Example 5) by accenting the dissonances agogically and accelerating through the change of harmony in m. 3.1. In general, increasing numbers of short arches crowd out this kind of rhetorical use of rubato.
Performers' increasing tendency to use tempo arching for smaller groups of measures creates a sense of rhythmically smooth predictability as to where tempo fluctuation will occur; acceleration becomes gradually more likely to be followed shortly by deceleration. This is part of the story about how, while the total amount of tempo fluctuation has not changed, its location and the priorities that undergird its use have. Rubato has become more periodic, as the simple sweep of directed motion allows us to visualize each phrase as though it were the progress of an ocean wave, or feel it as though we were breathing slowly. 16 Cook (2007) describes how Paderewski's performance of a Chopin Mazurka comes from the salon tradition, whereas modern performances (he gives the example of Fou Ts'ong) are mediated by the long distances and rich acoustics of the concert hall. An architectural or diachronic projection of musical time thus replaced the element of surprise, the synchronic or immediate act of listening. 17
Metrical Patterning
Tempo arching and phrase-final lengthening show how performance practice has changed on the large scale. A more granular approach reveals even more about where pianists employ rubato and how their tendencies to employ it in different kinds of locations has shifted. Metrical patterning in each recording was measured by averaging melody IOIs for each beat of the measure in mm. 1-48 and then dividing them by the average length of the measure. To negate the impact of final lengthening and large-scale tempo arching on metrical patterning, average lengths of beats were calculated using measures that do not include the beginnings and ends of phrase: mm. 1, 8, 9, 16, 17, 35, 36 and 29-49 were thus excluded. Figure 10 shows average melody IOI for each beat of the measure, expressed as a proportion of the average measure's length, plotted against the year of performance.
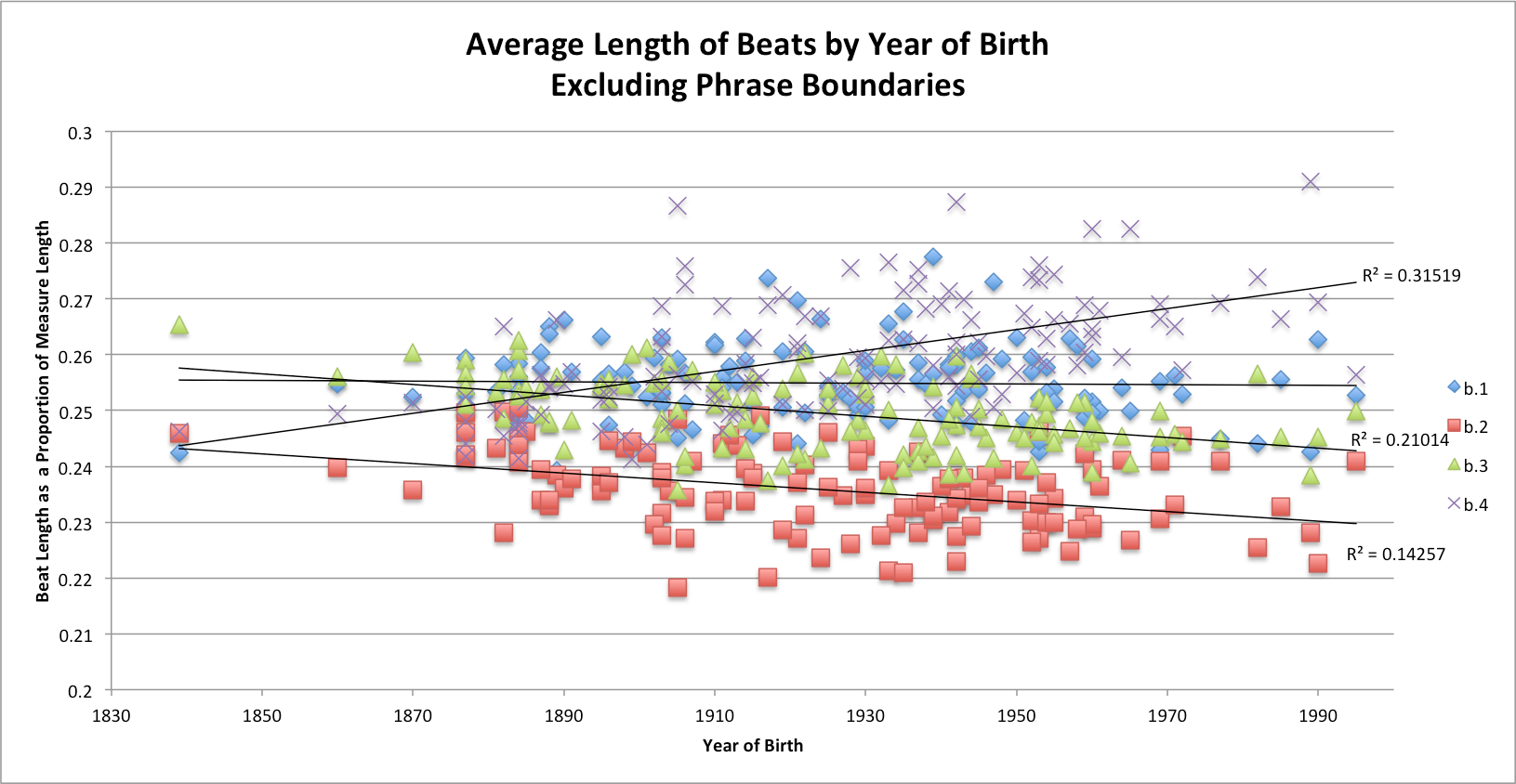
Figure 10. Scatterplot with linear fit lines of each beat's average proportion of the measure, vs. year of birth. Excludes the first and last measures of each phrase.
The broad hierarchy is clear, although individual performances show many exceptions. The fourth beat is longest, followed by first beats, third beats and second beats. 18 Trend lines illustrate the growing tendency to lengthen fourth beats at the expense of second and third beats; statistics for these trend lines are shown in Table 2. The divergence of beat proportions shows that lengthening is happening more and more consistently on beats one and four in later performances. 19
| Linear regression of Year of Birth with Duration of: | R2 | F(1,125) | p | B | β |
|---|---|---|---|---|---|
| 2nd Beats | .14 | 20.79 | <.001 | -.000086 | -.38 |
| 3rd Beats | .21 | 33.26 | <.001 | -.000095 | -.46 |
| 4th Beats | .32 | 57.53 | <.001 | -.000188 | .56 |
For pianists born before the turn of the 20th century, fourth beats were almost never the longest of the four on average; for pianists born since 1960, they always are. At the measure level, these graphs show a significant change in the kind of rubato pianists employ. Slower tempi in the later recordings are unlikely to be responsible for the increasing length of fourth beats. Controlling for year of birth, median tempo is not correlated with beat proportions (p > .05 in all cases).
The different timing strategies of Ganz (1919, b.1877) and Bonnecaze (1999, b.1965) typify the broad changes illustrated by diverging metrical proportions. The two pianists play with almost identical amounts of beat-to-beat tempo change, although Ganz plays a bit quicker overall. Ganz's average measure is more even than Bonnecaze because his choices of beats to lengthen are more varied. Video Example 2 shows melody IOIs for the first sixteen measures of each performance. In twelve of the sixteen measures, Bonnecaze's fourth beat is longest. Eleven of these have the same basic shape—long first beats, shorter second and third beats, longest fourth beats. Ganz also lengthens fourth beats, but usually as a prelude to an even longer first beat. Ganz favors first beats for his agogic climaxes; they are longest in nine of Ganz's measures. More importantly, Ganz's measures do not have a repeating basic shape, making his agogic nuances less predictable. 20 Lengthening dissonances on first beats gives the impression of clinging to the expressive moment as it flees, while lengthening a fourth beat before a dissonance serves as preparation or warning.
Agogic Accents
Empirical analyses of rubato have tended not to examine the role of changes of harmony and dissonance at the surface level. Palmer's (1996) tension-relaxation model combines surface dissonance and harmony distance, based on the circle of fifths, into a single measure. Her discussion of the correlation between this model and the actual performance being analyzed does not include granular detail about the kinds of events that motivate expressive timing strategies. Todd (1995) starts from a model that ignores the role of dissonance and harmony. Benadon and Zanette (2015), Cook (1987) and Dodson (2011a) focus on interactions between expressive timing and harmonic structure. Milsom and Peres da Costa (2014) call for closer examination of "special moments of deliberate and enhanced agogic accentuation in modeling expressive performance," (p. 83) noting that the rhetorical style espoused by 19th-century theorists contradicts the phrase-arch model of performance. Elements of both styles can co-exist in the same performance. The low points of tempo arches, particularly in shorter units, often create agogic accents, and pianists do not apply arching equally across the entire performance.
Analysis of recordings of Chopin's Etude, Op. 25 no. 1, shows that strategies of agogic accentuation have changed significantly since the early 20th century. Early 20th-century performers tended to use agogic lengthening for accented dissonances, changes of harmony and melodic inflections. Modern performers increasingly delay the arrival of those events, such that lengthening the melody IOI of an important event is no longer the default option for the most recent generation.
Friberg and Sundberg's (1995) research, the findings of which are consistent with those of previous experiments, suggests that the minimum threshold for perceiving timing deviation is about 5% of the tempo-defining IOI. 21 Ignoring the sextuplets' role in defining rhythm, I therefore used this measure as a conservative estimate of the difference between the intentional and unintentional timing deviations made by the highly skilled performers whose recordings were analysed in the present study. Therefore, a melody IOI was considered an agogic accent if one of the following conditions is true: it is longer than both the preceding and following IOIs by 5% of the prevailing tempo; it is longer than the preceding IOI by 10% of the prevailing tempo and longer than the following IOI; it is longer than the following IOI by 10% of the prevailing tempo and longer than the preceding IOI. Prevailing tempo is defined as the average of the nearest five melody IOIs (that is, the accent IOI, the two preceding and the two following IOIs). In absolute terms, the threshold ranges from about 25 milliseconds on both sides of an accent IOI or 50 ms on one side in the fastest recording (Koczalski [1938, b.1884], median tempo=120) to 42/84 ms in the slowest (Fialkowska [1997, b.1951], median tempo=71). For this analysis all the measures with a melody were included (mm. 1-44), while the coda's harmonically static arpeggios were excluded. Video Example 3 shows how this agogic definition works in practice. The first eight measures of two performances—one fast, one slow—are marked with melody IOIs and the ">" sign for agogic lengthening.
There is no correlation between the total number of agogic accents in a performance and the year of performance or performer's year of birth. However, the location of those accents within the measure has not remained constant over time. Figures 11 and 12 show a strong and significant trend over time whereby the proportion of agogic accents that fall on the third beat to total agogic accents in a performance declines, R2 = .25, F(1,125) = 41.51, p < .001, and the proportion of agogic accents that fall on the fourth beat increases, R2 = .32, F(1,125) = 57.93, p < .001. The proportion of agogic accents on fourth beats to total agogic accents is more strongly a function of year of birth (β = .53, p < .001) than of median tempo (β = -.17, p = .02), Adj. R2 = .34, F(2,124) = 32.70, p < .001. The proportion of first beat agogic accents to total agogic accents also decreases by year of birth, but at much slower rate, R2 = .06, F(1,125) = 8.22, p < .01. The proportion of agogic accents on the second beat of the measure has remained constant over time.
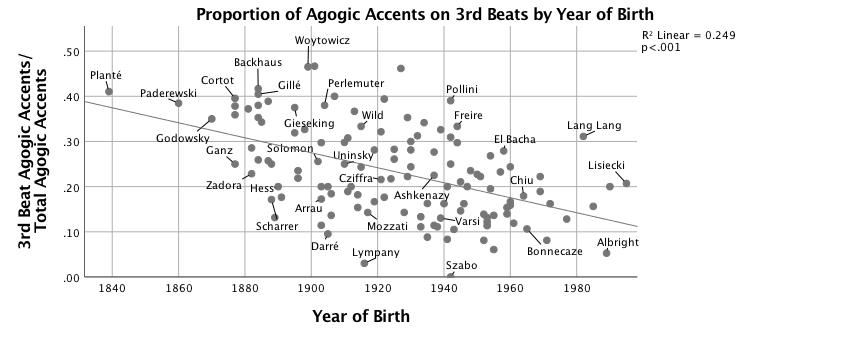
Figure 11. Scatterplot with linear fit line of proportion of beat-three agogic accents to total agogic accents vs. year of birth
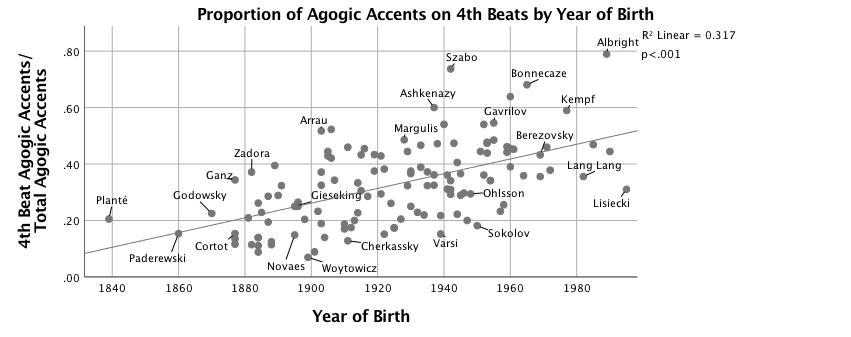
Figure 12. Scatterplot with linear fit line of proportion of beat-four agogic accents to total agogic accents vs. year of birth.
The main motivators of agogic accents are changes of harmony, metrically-accented dissonances in the melody, and changes of melodic direction from ascending to descending motion (that is, peaks). The taxonomy presented by Parncutt (2003), implemented in a computer model by Bisesi et al. (2011), also contains grouping accents and metrical accents. 22 In the present analysis, the role of grouping accents is captured mainly by tempo arching. Metrical accents universally coincide with changes of harmony, dissonances and melodic inflections. With changes of harmony, dissonance or chromatic tones introduced over the same bass note are included if there was no dissonance or chromaticism on the previous quarter note. For example, m. 4.3 is a change of harmony, but m. 6.2 is not. Thus in the present system dissonances in the harmony are described as changes of harmony, while metrically-accented dissonances in the melody are given their own category. This reflects the dominant role of melody in expressive timing. The term "delaying accents" will be used to describe agogic accents that occur one beat before changes of harmony, metrically-accented melodic dissonances and changes of melodic direction. The proportion of delaying accents to total agogic accents has increased significantly over time, R2 = .22, F(1,125) = 35.76, p < .001. The later the year of the pianist's birth, the larger the proportion of delaying accents in their performance, by an additive increase of .2% each year, β = .47, p < .001. 23
Because so many beats in Chopin's Etude, Op. 25 no. 1, feature one or more of the events listed above, the data are broken down into various types. Figures 13 and 14 show the difference between agogic accents that occur on the melody IOI of the accented dissonance or change of harmony and those that occur on the previous melody IOI; negative values represent a preponderance of delaying accents. 24 The unstandardized coefficients (B) in Table 3 show that the proportion of delaying accents has increased more quickly for changes of harmony than for accented dissonances or melodic inflections. Pianists who favor delaying accents tend to do so for all three types of events. Percentage of delaying accents on changes of harmony is correlated with percentage of delaying accents on melodic inflections (r = .57, p < .001) and accented dissonances (r = .68, p < .001); percentage of delaying accents on melodic inflections is correlated even more strongly with percentage of delaying accents on accented dissonances (r = .80, p < .001).
| Linear regression of Year of Birth with Difference Between On-Beat and Delaying Accents for: | R2 | F(1,125) | p | B | β |
|---|---|---|---|---|---|
| Accented Dissonances | .20 | 31.75 | <.001 | -.088 | -.45 |
| Changes of Harmony | .16 | 24.51 | <.001 | -.111 | -.41 |
| Melodic Inflections | .06 | 8.10 | <.01 | -.063 | -.25 |
Delaying the arrival of a change of harmony was never an uncommon practice; note that many earlier pianists appear below the line indicating 0 in Figure 13, whereas very few early pianists consistently delayed accented dissonances (Figure 14).
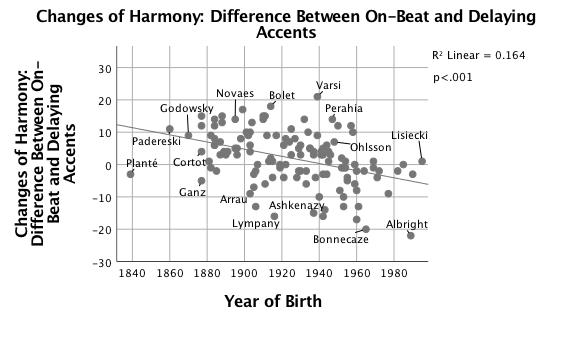
Figure 13. Scatterplot with linear fit line of difference between agogic accents occurring on the beat of changes of harmony and those occurring on the beat before vs. year of birth.
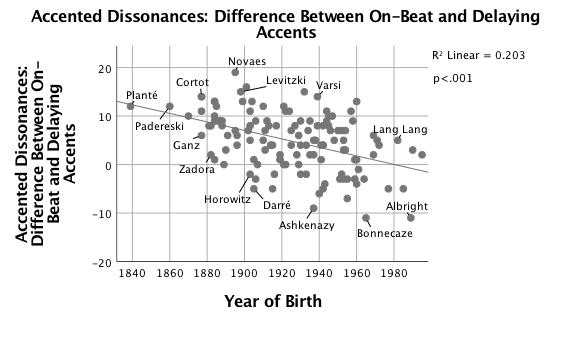
Figure 14. Scatterplot with linear fit line of difference between agogic accents occurring on the beat of accented dissonances and those occurring on the beat before vs. year of birth.
The delayed change of harmony has recently become a strong default option. Melodic inflections show a slower trend towards delaying accents, and year of birth is a weaker predictor than for accented dissonances and changes of harmony. 25 Controlling for year of birth, there is no correlation between each type of event and median tempo, p > .05.
Accented dissonances, changes of harmony and melodic inflections very often occur simultaneously, most often on the first beat. In fact, the first beat of every measure in the etude features one or more of these events; in a piece of smooth, flowing and uniform texture, they are Chopin's primary means of delineating meter. Two hypotheses can be proposed to explain the lengthening of fourth beats over time and the greater prominence of agogic stress on the fourth beat. First, modern pianists lengthen fourth beats irrespective of the musical context. They have a characteristic way of playing a measure in 4/4 time that tends to lengthen the fourth beat more than earlier performers. Second, modern pianists tend to lengthen the melody IOI before an important musical event, as opposed to earlier pianists who tended to lengthen the IOI of the event itself. These hypotheses can be tested by examining dissonance, change of harmony and inflection on third beats. The difference between on-beat and delaying accents for third beats shows the same trend as those described in Table 3: R2 = .12, F(1,125) = 16.61, p < .001, B = -.056, β = -.34. The small, although statistically significant, increase over time of lengthening a second beat to highlight an event on the following third beat is not a function of metrical patterning. Figure 10 above shows second beats decreasing in length. Increasing numbers of agogic accents on fourth beats are not merely the consequence of groove. The evidence points to a gradual shift towards greater acceptance of delaying an important event instead of lengthening after it occurs.
The almost imperceptibly slow shifts illustrated in Figures 11-14 show how Slåttebrekk and Harrison (2010) could arrive at the view that the difference between Grieg's playing style and modern interpretations is of crevasse-like proportions:
Another element, never found in Grieg's performances, is the usual procedure today of emphasising a single note or a chord by adding time immediately before them. This 'holding' or waiting in order to heighten the effect of an accentuation, intensifying the expression or adding general weight to the performance, is very alien to Grieg. Quite the contrary, Grieg's impulse to a new phrase or the placing of the climax of a phrase, is almost inevitably slightly before the projected beat, a projected beat being where we would expect the beat to appear.
Perhaps surprisingly, the documentary evidence from the late 19th century predicts pianists' use of agogic accents in the early recordings. Riemann (1888/1892) makes clear exactly where the agogic emphasis should fall: "the usual dynamic signs [cresc. and decresc.] apply also to the 'agogics', and the chief lengthening (the agogic accent) falls on the most accented note; therefore in the limits of the bar the one directly following the bar-line." (p. 64) 26 In light of this and early recorded practice, when Lussy (1874/1896) advises performers to slow down "on expressive notes" (p. 167) he most likely means the note itself, not the beat before.
The "'holding' or waiting" described by Slåttebrekk and Harrison, above, is common in the phrasing of 21st-century pianists, but rarely referred to explicitly in writing. Boris Berman (2000), cautions:
against a bad habit that creeps into the playing of too many performers: hesitation before the downbeat, which can become a constant feature of one's playing… At the root of this habit is probably a desire to emphasize the importance of the downbeat, but the result is terribly unnatural and often irritating. This agogic accent is often better achieved by getting to the important musical point without any hesitation and lingering on it slightly… I myself suffered from this ailment at one time and had difficulty purging my playing of it. (pp. 95-96)
One of the only descriptions of the metrical patterning and delaying accents noted in this study thus comes from a performer swimming against the tide. Slåttebrekk's and Harrison's description arises out of a recognition of stylistic difference as well.
Using linear regression to describe trends in performance practice obscures some details of how style changes. The real correlation between year of birth and tendency to use delaying accents may, in fact, be stronger than suggested above. For example, Darré (1946, b.1905) and Lympany (1995, b.1916), two older pianists who tend to lengthen second beats in preparation for an event on the following third beat, are not obvious examples of performers whose agogic accentuation delays the arrival of important events. Both play certain passages in an unusual lilting way, lengthening beats two and four, creating a 2/4 feel. Metrical patterning is difficult to distinguish from agogic accentuation in these recordings; Audio Example 6 shows an extreme passage from Darré's recording.
The best example of the style that accentuates events by lengthening the beat before is in Ashkenazy's recording (1975, b.1937). Video Example 4 shows the first eight measures with agogic accents on melody IOIs marked; note that the small peaks at 1.4 and 2.4 fall below the significance threshold used in this study. The progressively increasing size of agogic accents on the fourth beat of the measure creates a hierarchically organized phrase. The accents guide our listening to the important events on the first beat of the measure. Ashkenazy is not the only pianist to utilize this style, although consistent application of the delaying accent is unusual. Gavrilov (1985, b.1955), Zayas (1983, b.1940), Szabó (1971, b.1942) and Kempf (2003, b.1977) show the same tendency to highlight both dissonances and changes of harmony by stretching the beat before. At the same time, we can witness the development of a style that emphasizes a smooth and gentle rocking motion rather than the use of agogic accents to emphasize musical events in the score. The lower-rightmost point in Figure 14 represents Albright's performance (2010, b.1989). Video Example 5 shows the first eight measures of this recording. A regular metrical pattern persists irrespective of changes of harmony or melodic events.
At the other end of the spectrum is the recording made by Novaes (1958, b.1895), in which melodic and harmonic events are highly correlated with agogic accents. As shown in Video Example 6, Novaes stretches beats with dissonances and changes of harmony. Of the two fourth-beat agogic accents, the first emphasizes the dissonant leap in the bass (m. 6.4) rather than the downbeat that follows, and the second ends the phrase (m. 8.4). Performances in which the first beat tends to be emphasized are less likely to give an impression of metrical patterning than those of Albright (2010) and Bonnecaze (1999). Varsi (1982, b.1939) is the pianist who places the most agogic accents on the first beat (32), and Bonnecaze plays the most on the fourth (32), closely followed by Albright (30). Varsi (1982, b.1939), Mozzati (1984, b.1917) and Perahia (2001, b.1947) play the longest first beats as a proportion of the measure. Of these only Varsi provides a sense of groove: see Video Example 7. Most pianists take care not to be predictable in the measure-to-measure application of rubato.
CONCLUSION
Use of rubato in Chopin's Etude, Op. 25 no. 1, has changed significantly since the first recordings, although the overall amount of tempo fluctuation has not. The main evidence of this is the lengthening, on average, of pianists' fourth beats and corresponding shortening of beats two and three. Several factors contribute to the change of style: an increase in the frequency and amount of phrase-final lengthening, the use of tempo arches over shorter groups of measures, and a tendency to mark accented dissonances and changes of harmony by lengthening the previous beat. Taken together, it can be inferred from increases in final lengthening and tempo arching that pianists had a growing sense that they should use timing as a way of delineating clearly the grouping structure of the work.
Increasing two-measure tempo arching comes at the expense of marking accented dissonances agogically. Two-measure arches do not inherently suggest delaying accents or the lengthening of the fourth beat; for every lengthened fourth beat, the arch predicts a shortened fourth beat one measure later. The conflict between these two timing strategies is more philosophical. Short tempo arches and delaying agogic accents increase the listener's feelings of smoothness and predictability. In this sense the use of these strategies embodies a structuralist or architectural attitude towards musical time. The on-beat agogic, a reaction to the musical event after the fact, dramatizes the element of surprise, a synchronic attitude towards music which is currently unfashionable.
The present analysis of recordings of Chopin's Etude, Op. 25 no. 1, which reveals subtle changes in performance practice, has several broader lessons for the study of historical performance. Of course, more research is needed to discover whether the trends identified are also to be found in performances of works beyond this small corner of the repertoire. So much of the literature on early 20th-century performance practice relies on the discussion of idiosyncrasies. The present study addresses differences between early-recorded and more modern performances, analyzing data that show changes over time, which are not sudden but almost imperceptibly slow: trends in ways of interpreting a score. We can only imagine what similar accretions of minute stylistic changes led to the features that characterize the earliest recordings; documentary evidence alone cannot possibly tell the story. The changes to the deeply ingrained practices illustrated in the present study can help to calibrate the baseline for thinking about earlier, unrecorded performance styles. Some of the less-obvious rules underlying expressive performance have shifted and are still shifting.
ACKNOWLEDGEMENTS
This article was copyedited by Matthew Moore and layout edited by Diana Kayser.
NOTES
-
Correspondence can be addressed to: Michael Rector, University of Wisconsin-Green Bay, 2420 Nicolet Dr., Green Bay WI, 54304. Email: rectorm@uwgb.edu
Return to Text -
For this study, tempo fluctuation refers to the variance, construed informally as how far a group of numbers is spread apart, of tempo data measured at each beat of the etude. Specific measures are defined below.
Return to Text -
The term "rubato" refers to a special case of tempo fluctuation that seems intentional.
Return to Text -
Phrase-final lengthening refers to the practice of slowing down at the end of a phrase, and is measured as the difference between the prevailing tempo and final tempo of a phrase. Inter-onset interval is the amount of time between the attacks of two successive notes; melody inter-onset interval here refers to the amount of time between the attacks of two successive melody notes.
Return to Text -
Similar slowing has been observed in many empirical studies of performance practice, including Philip (1992, 2004), Cook (2007), and Katz (2003). Bowen (1996) shows speeding up in some pieces, slowing in others and no overall trend in the 18h- and 19th-century symphonic repertoire he examined.
Return to Text -
Standard deviation measures the dispersion of data from the mean. For example, a change of tempo for a certain section of an otherwise metronomic performance will lead to a higher standard deviation measurement, although the performance lacks rubato in the beat-to-beat sense.
Return to Text -
Repp (1998) has argued that the grand average is not a "meaningless statistical conglomerate" (p. 1090) but should be considered typical, showing in an earlier experiment listeners' high estimation of the aesthetic quality of such a performance (Repp, 1997).
Return to Text -
Mm. 36-44 show a small increase, but the statistical significance depends on an outlier, R2 = .04, F(1,125) = 4.55, p = .04. Koczalski's (1938, b.1884) lengthening proportion of -.36 is far below the next lowest—Wild (1992, b.1915) at -.13.
Return to Text -
Many recent studies have found evidence against the notion, first articulated in the empirical literature by Philip (1992), that diversity in performance is declining. See November (2011), Fabian and Schubert (2008), and Fabian (2006, 2014).
Return to Text -
Accompanying files can be accessed at: http://hdl.handle.net/1811/92831
Return to Text -
Christiani (1885): "First Rule: The termination of a period (8-bar group) is shown by the appearance of the old, or commencement of a new subject … Second Rule: Each metrical group should be as much as possible a unit in itself. Periodizing should respect this unity and not cut into it." (p. 117)
Return to Text -
For the idea that early recordings reflect unrecorded 19th-century practice, see Leech-Wilkinson (2009).
Return to Text -
Sapp (2011) uses the same method of comparing tempo data to "prototype arches at all time scales," (p. 39) although he uses a sine wave rather than a quadratic function as a model.
Return to Text -
β is the standardized coefficient of each variable in the linear model, indicating in this case how much two-measure arching increases for each year later a pianist was born or decreases for each unit of median tempo. Performer's year of birth is more than twice as strong a predictor as median tempo.
Return to Text -
e.g., Lussy (1874/1896, p. 165), Behnke and Pearce's Voice-Training Primer of 1893 (as cited in Philip, 1992, p. 39).
Return to Text -
For a detailed discussion of the physical, "kinematic" analogy in terms of tempo arcs see Todd (1995).
Return to Text -
Day (2000, p. 151) uses the analogy of storytelling.
Return to Text -
The proportional length of fourth beats is moderately skewed (.553), Shapiro-Wilk's test p = .01, by the presence of some very high values (greater than .28) in the recordings of performances by Albright, Szabó, Kentner, Bonnecaze and Matsuzawa. The large sample size and low p-values obtained by the analysis suggest that the results are still robust.
Return to Text -
These changes in average beat length also suggest that Clynes's (1995) concept of the "composer's pulse," may be historically conditioned, at least in its temporal dimension, and, given the smaller variance in average beat lengths in early performances, perhaps even a by-product of performance practice in a certain era.
Return to Text -
In their corpus study of Bach's Prelude in C major (WTC I), Benadon and Zanette (2015) liken this kind of repeating tempo shape to "groove" in jazz.
Return to Text -
"There is a middle IOI range of about 400 to 800 ms [75-150 beats per minute] where the relative jnd [just noticeable difference] is approximately constant. The jnd in that range is about 2% for tempo and between 4% and 6% for the other types of perturbation" (Friberg & Sundberg, 1995, p. 2527). Some recorded performances of Chopin's Etude, Op. 25 no.1, are slightly slower than indicated by this range of melody IOIs. Friberg and Sundberg's results showed a jnd of 5.2% at an IOI of 1 sec (60 beats per minute).
Return to Text -
Reflecting a 21st-century bias, Parncutt (2003) defines an agogic accent exclusively in terms of delay. He refers to lengthening the note itself as an articulation accent.
Return to Text -
Residuals are moderately skewed (skewness = .587, kurtosis = .058, Shapiro-Wilk test p = .01). Given the very low p-value for the linear regression, the single-variable model is still robust.
Return to Text -
The beat-earlier agogic accent, or delay of the important note, is described in Clarke (1995, p. 15).
Return to Text -
For melodic inflections, year of performance (r = -.28, p = .001) is a slightly better predictor than year of birth (r = -.25, p = .005).
Return to Text -
Cook (2013, p. 210) argues that Riemann's advocacy of phrase arching should be understood within the context of a highly rhetorical style.
Return to Text
REFERENCES
- Barolsky, D. (2007). The performer as analyst. Music Theory Online, 13(1). https://doi.org/10.30535/mto.13.1.6
- Benadon, F. & Zanette, D. (2015). A corpus analysis of rubato in Bach's C Major Prelude WTC I. Music Performance Research, 7, 1-26.
- Berman, Boris. (2000). Notes from the pianist's bench. New Haven, CT: Yale University Press.
- Bisesi, E., Parncutt R. & Friberg, A. (2011). An accent-based approach to performance rendering: Music theory meets music psychology. In Proceedings of the International Symposium on Performance Science. (pp. 27-32) National Library of Sweden.
- Bowen, J. A. (1996). Tempo, duration, and flexibility: Techniques in the analysis of performance. The Journal of Musicological Research, 16, 111-56. https://doi.org/10.1080/01411899608574728
- Brown, C. (1999). Classical and romantic performing practice: 1750-1900. New York, NY: Oxford University Press. https://doi.org/10.1093/acprof:oso/9780198161653.001.0001
- Burkhart, C. (1997). Chopin's 'concluding expansions.' In D. Witten (Ed.), Nineteenth century piano music: Essays in performance and analysis (pp. 95-116). New York, NY: Garland.
- Cannam, C., Landone, C. & Sandler, M. (2010). Sonic Visualiser: An open-source application for viewing, analysing, and annotating music audio files. In Proceedings of the ACM Multimedia International Conference, October 25–29, Firenze, Italy. https://doi.org/10.1145/1873951.1874248
- Christiani, A. (1885). Principles of expression in pianoforte playing. Harper and Brothers.
- Clarke, E. (1982). Timing in the performance of Erik Satie's "Vexations." Acta Psychologica, 50, 1-19. https://doi.org/10.1016/0001-6918(82)90047-6
- Clarke, E. (1985). Structure and expression in rhythmic performance. In P. Howell (Ed.), Musical structure and cognition (pp. 209-236). Cambridge, MA: Academic Press.
- Clarke, E. (1995). Expression in performance: Generativity, perception and semiosis. In J. Rink (Ed.), The practice of performance (pp. 21-54). Cambridge, UK: Cambridge University Press. https://doi.org/10.1017/CBO9780511552366.003
- Clynes, M. (1995). Microstructural musical linguistics: Composers' pulses are liked most by the best musicians. Cognition 55(3), 269-310. https://doi.org/10.1016/0010-0277(94)00650-A
- Cook, N. (1987). Structure and performance timing in Bach's C major prelude (WTCI): An empirical study. Music Analysis 6(3), 257-72. https://doi.org/10.2307/854205
- Cook, N. (1995). The conductor and the theorist: Furtwängler, Schenker and the first movement of Beethoven's Ninth Symphony. In J. Rink (Ed.), The practice of performance (pp. 105-25). Cambridge, UK: Cambridge University Press. https://doi.org/10.1017/CBO9780511552366.006
- Cook, N. (2007). Performance analysis and Chopin's mazurkas. Musicae Scientiae, 11, 183-207. https://doi.org/10.1177/102986490701100203
- Cook, N. (2009). Changing the musical object: Approaches to performance analysis. In Z. Blažeković (Ed.), Music's intellectual history (pp. 775-90). RILM.
- Cook, N. (2013). Beyond the score: Music as performance. Oxford, UK: Oxford University Press. https://doi.org/fqjs
- Day, T. (2000). A century of recorded music. New Haven, CT: Yale University Press.
- Dodson, A. (2002). Performance and hypermetric transformation: An extension of the Lerdahl-Jackendoff theory. Music Theory Online, 8(1). http://www.mtosmt.org/issues/mto.02.8.1/mto.02.8.1.dodson.html
- Dodson, A. (2008). Performance, grouping and Schenkerian alternative readings in some passages from Beethoven's 'Lebewohl' sonata. Music Analysis, 27(1), 107-34. https://doi.org/10.1111/j.1468-2249.2008.00269.x
- Dodson, A. (2011a). Expressive timing in expanded phrases: an empirical study of recordings of three Chopin preludes. Music Performance Research, 4, 2-29.
- Dodson, A. (2011b). Performance strategies in three recordings of Bach's Invention No. 1 in C major: A comparative study. Intersections, 31(2), 43-64. https://doi.org/10.7202/1013213ar
- Dubal, D. (2004). The art of the piano. 3rd ed. Portland, OR: Amadeus.
- Fabian, D. (2006) Is diversity in musical performance truly in decline? The evidence of sound recordings. Context, 31, 165-80
- Fabian, D. (2008). Classical sound recordings and live performances. In M. Dogantan-Dack (Ed.), Recorded music: Philosophical and critical reflections (pp. 232-60). Middlesex, UK: Middlesex University Press.
- Fabian, D. (2014). Commercial sound recordings and trends in expressive music performance. In D. Fabian, R. Timmers & E. Schubert (Eds.), Expressiveness in music performance (pp. 58-79). Oxford, UK: Oxford University Press. https://doi.org/10.1093/acprof:oso/9780199659647.003.0004
- Fabian, D. (2017). Analyzing difference in recordings of Bach's violin solos with a lead from Gilles Deleuze. Music Theory Online, 23(4). https://doi.org/10.30535/mto.23.4.4
- Fabian, D. & Schubert, E. (2008). Musical character and the performance and perception of dotting, articulation and tempo in 34 recordings of variation 7 from J. S. Bach's Goldberg Variations (BWV 988). Musicae Scientiae, 12(2), 177-206. https://doi.org/10.1177/102986490801200201
- Friberg, A. & Sundberg, J. (1995). Time discrimination in a monotonic, isochronous sequence. Journal of the Acoustical Society of America, 98, 2524-31. https://doi.org/10.1121/1.413218
- Katz, M. (2003). Beethoven in the age of mechanical reproduction: the violin concerto on record. Beethoven Forum, 10, 38-54
- Leech-Wilkinson, D. (2009). The changing sound of music: Approaches to studying recorded musical performance. London: CHARM. http://www.charm.rhul.ac.uk/studies/chapters/intro.html
- Leech-Wilkinson, D. (2015). Cortot's Berceuse. Music Analysis, 34(3), 335–63. https://doi.org/10.1111/musa.12054
- Lussy, M. (1874/1896). Musical expression. Trans. M. E. von Glehn. London: Novello, 1896. Paris: Heugel, 1874.
- Milsom, D. & Peres da Costa, N. (2014). Expressiveness in historical perspective: Nineteenth century ideals and practices. In D. Fabian, R. Timmers & E. Schubert (Eds.), Expressiveness in music performance (pp. 80-98). New York: Oxford University Press. https://doi.org/10.1093/acprof:oso/9780199659647.003.0005
- November, N. (2011). Performance history and Beethoven's string quartets: Setting the record crooked. Journal of Musicological Research, 30, 1–22. https://doi.org/10.1080/01411896.2010.515376
- Ohriner, M. (2012) Grouping hierarchy and trajectories of pacing in performances of Chopin's mazurkas. Music Theory Online, 18(1). https://doi.org/10.30535/mto.18.1.6
- Parncutt, R. (2003). Accents and expression in piano performance. In Perspektiven und Methoden einer systemischen Musikwissenschaft: Bericht über das Kolloquium im Musikwissenschaftlichen Institut der Universität zu Köln 1998 (pp. 163-85). Lang.
- Palmer, C. (1996). Anatomy of a performance: Sources of musical expression. Music Perception, 13(3), 433-53. https://doi.org/10.2307/40286178
- Peres da Costa, N. (2012). Off the record: Performing practices in Romantic piano playing. Oxford, UK: Oxford University Press. https://doi.org/10.1093/acprof:oso/9780195386912.001.0001
- Philip, R. (1992). Early recordings and musical style: Changing tastes in instrumental performance 1900-1950. Cambridge, UK: Cambridge University Press. https://doi.org/10.1017/CBO9780511470271
- Philip, R. (2004). Performing music in the age of recording. New Haven, CT: Yale University Press.
- Repp, B. (1992). Diversity and commonality in music performance: An analysis of timing microstructure in Schumann's "Träumerei." The Journal of the Acoustical Society of America, 92(5), 2546-68. https://doi.org/10.1121/1.404425
- Repp, B. (1997). The aesthetic quality of a quantitatively average music performance: Two preliminary experiments. Music Perception, 14(4), 419-44. https://doi.org/10.2307/40285732
- Repp, B. (1998). A microcosm of musical expression. I. Quantitative analysis of pianists' timing in the initial measures of Chopin's Etude in E major. The Journal of the Acoustical Society of America, 104(2), 1085-1100. https://doi.org/10.1121/1.423325
- Riemann, H. (1888/1892). Catechism of pianoforte playing. London: Augener & Co. Leipzig: 1888.
- Rink, J. (2001). The line of argument in Chopin's E minor prelude, Early Music, 29, 435-44. https://doi.org/10.1093/earlyj/XXIX.3.434
- Rink, J. (2015). The (f)utility of performance analysis. In M. Doğantan-Dack (Ed.) Artistic practice as research in music: Theory, criticism, practice. Burlington, VT: Ashgate. https://doi.org/10.4324/9781315568041
- Rink, J., Spiro, N., & Gold, N. (2011). Motive, gesture and the analysis of performance. In A. Gritten & E. King (Eds.) New Perspectives on Music and Gesture (pp. 267-92). Burlington, VT: Ashgate. https://doi.org/10.4324/9781315598048
- Sapp, C. (2011). Computational methods for the analysis of musical structure (Unpublished doctoral dissertation). Stanford University, Palo Alto, CA.
- Spiro, N., Gold, N., & Rink, J. (2010). The form of performance; Analysing pattern distribution in select recordings of Chopin's Mazurka Op. 24 no. 2. Musicae Scientiae, 14, 23-55. https://doi.org/10.1177/102986491001400202
- Slåttebrekk, S. & Harrison, T. (2010). Chasing the butterfly: Recreating Grieg's 1903 recordings and beyond. http://www.chasingthebutterfly.no/
- Timmers, R., Ashley, R., Desain, P. & Heijink, H. (2000). The influence of musical context on tempo rubato. Journal of New Music Research, 29(2), 131-58. https://doi.org/10.1076/jnmr.29.2.131.3095
- Todd, N. (1985). A model of expressive timing in tonal music. Music Perception, 3(1), 33–57. https://doi.org/10.2307/40285321
- Todd, N. (1989). A computational model of rubato. Contemporary Music Review, 3(1), 69-88. https://doi.org/10.1080/07494468900640061
- Todd, N. (1992). The dynamics of dynamics: A model of musical expression. Journal of the Acoustical Society of America, 91(6), 3540-50. https://doi.org/10.1121/1.402843
- Todd, N. (1995) The kinematics of musical expression. Journal of the Acoustical Society of America, 97(3), 1940-49. https://doi.org/10.1121/1.412067
- Windsor, W. L. & Clarke, E. (1997) Expressive timing and dynamics in real and artificial musical performances: Using an algorithm as an analytical tool. Music Perception, 15(2), 127-52. https://doi.org/10.2307/40285746
| Albright, C. | 2010 | CAPC: (UPC 884501469760) |
| Anda, G. | 1955 | Musical Heritage Society: 5296942 (2010) |
| Anievas, A. | 1968 | EMI: 5 74290 2 (2001) |
| Arrau, C. | 1929 | Pearl: GEMS 0070 |
| Arrau, C. | 1956 | EMI Classic: 0946 3 79988 2 3 (1987) |
| Ashkenazy, V. | 1960 | Melodiya: SUCD 10-00511 |
| Ashkenazy, V. | 1975 | London: 414 127-2 (1984) |
| Bachauer, G. | 1963 | Mercury: SR 90368 |
| Backhaus, W. | 1909 | Victor: 74159 |
| Backhaus, W. | 1928 | HMV: DB 1178 |
| Backhaus, W. | 1951 | London: LL 1556 |
| Badura-Skoda, P. | 1962 | Kleos: 5117 (2004) |
| Barnett, D. | 1981 | Ledgebrook: LA 002 |
| Berezovsky, B. | 1991 | Apex: 8573 89083 2 (2001) |
| Berezovsky, B. | 2005 | Warner Classics: 2564 62258-2 |
| Biret, I. | 1990 | Naxos: 8.550364 |
| Bolet, J. | 1985 | Decca: 417 361-2 (1987) |
| Bonnecaze, V. | 1999 | Arcobaleno: AAOC-94362 |
| Brailowsky, A. | 1932 | Danachord: DACOCD 337 (1989) |
| Brailowsky, A. | 1946 | RCA Victor: LM-6000 |
| Brancart, E. | 2003 | Delos: DE 3411 |
| Broman, N. | 1919 | Caprice: 21677 (2010) |
| Browning, J. | 1968 | BMG Classics: 60131-2-RV (1989) |
| Cherkassky, S. | 1955 | Phillips: 456 742-2 (1998) |
| Chiu, F. | 2004 | Harmonia Mundi: HMU 907282 |
| Chochieva, Z. | 2014 | Piano Classics: PCL0068 |
| Cortot, A. | 1925 | Pearl: Gemm CD 9386, |
| Cortot, A. | 1934 | Phillips: LC-0305 1999 |
| Cortot, A. | 1943 | EMI Classics: CDZF 67359 (1991) |
| Cziffra, G. | 1962 | Phillips: 456-760-2 (1999) |
| Darré, J.-M. | 1946 | VAI: VAIA /IPA 1065-2 (1994) |
| Duchable, F.-R. | 1980 | Erato: ECD88001 (2014) |
| Dupont, J. | 1933 | Pathé: PG9 |
| Ebi, A. | 1990 | Camerata: 25CM-609 (2000) |
| El Bacha, A. R. | 2009 | Forlane: 16790 |
| Fialkowska, J. | 1997 | Atma classique: ACD2 2554 |
| Francois, S. | 1959 | EMI: 50999 646114 2 7 (2010) CD 7 |
| Freire, N. | 2002 | Decca: 470 288-2 |
| Ganz, R. | 1919 | Pathé: 27024 |
| Gavrilov, A. | 1985 | EMI Seraphim: 74502 (2001) |
| Geniusas, L. | 2016 | Dux: 1294 |
| Gieseking, W. | 1925 | APR: 6013 (2013) |
| Gillé, V. | 1950 | Private tape from Sakuraphon CD 33012 |
| Gimpel, J. | 1978 | Cambria: CD-1070A |
| Godowsky, L. | 1924 | APR: 7013 (1991) |
| Goldsand, R. | 1955 | Concert Hall Society: 1133 |
| Gulda, F. | 1948 | Decca: K2167 (AR_13012-2) |
| Hagiwara, T. | 2006 | Stillwater: 011 |
| Hambourg, M. | 1996 | Arbiter 2004 (in Dubal: The Art of the Piano) |
| Hess, M. | 1937 | APR: 5549 (2001) |
| Hobson, I. | 2004 | Zephyr: z139-10 (2010) |
| Hoffman, L. | 1975 | Sine Qua Non: 7721 |
| Holtham, I. | 1994 | Move Records: MD 3134 |
| Horowitz, V. | 1989 | Sony: SK 45818 |
| Jenner, A. | 1951 | Remington RLP 199-28-A |
| Karolyi, J. von | 1956 | Jube: 1284 (2014) |
| Katin, P. | 1993 | Pickwick: ORCD 11001 |
| Kempf, F. | 2003 | Musical Heritage Society: 5197442 |
| Kentner, L. | 1959 | Capitol: GBR-7162 |
| Kersenbaum, S. | 1975 | Music for Pleasure: EMI CFP 40239 |
| Kilenyi, E. | 1941 | American Columbia: M-473 |
| Koczalski, R. | 1938 | Marston: 53016-2 (2015) |
| Kozina, Z. | 1982 | Panton: 8111 0233 |
| Krieger, N. | 1989 | VOX: ACD 8760 |
| Kuerti, A. | 1971 | Monitor: MCS 2133 |
| Lang, L. | 2010 | Sony: 88697 71901 2/1 |
| Lausnay, G. de | 1928 | Pathé: X5437 |
| Levitzki, M. | 1923 | Naxos Historical: 8.110688 (2002) |
| Liberace | 1954 | Columbia: ML 4900 |
| Lisiecki, J. | 2013 | DG: LC0173 |
| Lopes, F. | 1994 | L'art: 38 |
| Lortat, R. | 1931 | French Columbia: LFX-139 |
| Lortie, L. | 1986 | Chandos: 8482 |
| Lugansky, N. | 1999 | Erato: 8573802282 |
| Lympany, M. | 1995 | Erato: 0630-11726-2 |
| Magaloff, N. | 1975 | Phillips: 420 705-2 |
| Margulis, V. | 1994 | Point Classics: 267114-2 |
| Matsuzawa, Y. | 1996 | Novalis: 150 142-2 (1997) |
| Moravec, I. | 1989 | Dorian: 90140 |
| Mozzati, A. | 1984 | Funk and Wagnalls: 603B |
| Nissman, B. | 2003 | Pierian: 0019 |
| Novaes, G. | 1958 | VOX: 510.930 |
| Ogdon, J. | 1985 | Altarus: 9072 (1993) |
| Ohlsson, G. | 1998 | Arabesque: Z6718 |
| Orlovetsky, A. | 2005 | IM Lab: IMLCD135 |
| Orth, P. | 1982 | Music Masters: 20038 |
| Padereski, I. J. | 1912 | Pearl: Gemm CD 9323 (1988) |
| Perahia, M. | 2001 | Sony: SK 61885 |
| Perlemuter, V. | 1982 | Nimbus: 5095 (1987) |
| Petri, E. | 1951 | Pearl: GEMM CD 9966 |
| Planté, F. | 1928 | Arbiter: 150 (2006) |
| Pollini, M. | 1960 | Testament: JSBT-8473 (2011) |
| Pollini, M. | 1972 | DG: 00289 477 8423 (2009) |
| Pouishnoff, L. | 1948 | HMV: B9699 |
| Pritchard, R. | 1962 | Spoken Arts: 202 |
| Rubinstein, A. | 1964 | RCA: 63062-2 (1999) |
| Saperton, D. | 1952 | VAI: VAIA /IPA 1037-2 (1993) |
| Scharrer, I. | 1912 | Gramophone: D82 |
| Scharrer, I. | 1933 | English Columbia: DB 1348 |
| Schein, A. | 1959 | Kapp Classics: KCL 9023 |
| Serkin, R. | 1933 | DA: COCD 693 (2010) |
| Shebanova, T. | 2007 | Narodowy Instytut Fryderyka Chopina: CD 007 (2010) |
| Shebanova, T. | 2010 | IMC Music (via Amazon Music) |
| Sheyne, M. | 1951 | Allegro: AL 7 |
| Simon, A. | 1990 | Vox Unique: VU 9033 (1990) |
| Slenczynska, R. | 1978 | Musical Heritage Society: 3798 |
| Slobodyanik, A. | 1972 | Angel/Melodiya: SR 20405 |
| Smith, R. | 1990 | Nimbus: 5223 |
| Sokolov, G. | 1995 | Naïve: OP 30456 (2007) |
| Solomon C. | 1933 | Pearl: GEM 0177 (2002) |
| Szabó, C. | 1971 | Hungaroton: HCD 32088-90 |
| Szekely, I. | 1987 | Naxos: 8550083 |
| Thibaudet, J.-Y. | 1999 | Decca: 466 357-2 |
| Uninsky, A. | 1954 | Epic: LC 3065 |
| van den Hoek, M. | 1998 | Brilliant Classics: 99154 |
| Varsi, D. | 1982 | Intercord: 830.807 (1985) |
| Vasary, T. | 1965 | DG: 136454 |
| Vered, I. | 1972 | Connoisseur Society: 2056 |
| Virsaladze, E. | 1985 | Live Classics: 382 (1998) |
| Voskressensky, M. | 2015 | Classical Records: 166 |
| Watts, A. | 1991 | EMI Classics: CDC 7 54151 2 |
| Wild, E. | 1947 | Majestic: MZ2 |
| Wild, E. | 1992 | Chesky: 77 |
| Woytowicz, B. | 1959 | Jube: 1402 (2015) |
| Yokoyama, Y. | 1992 | Sony Classics: SK 62605 (1993) |
| Zadora, M. | 1922 | Polydor: 19078 |
| Zayas, J. | 1983 | Music and Arts: CD 891 (1995) |

