MUSIC is replete with repeated patterns—patterns of pitch, interval, and rhythm. Figure 1 shows ten themes from Barlow and Morgenstern's Dictionary of Musical Themes (1948). (This small sample—created only for purposes of illustration—represents the first ten composers in the book and shows the first theme listed for each composer; in the book, both composers and pieces are listed alphabetically.) Four of the ten themes (C, G, H, and I) contain repeated pitch patterns (indicated with solid brackets). Five (A, B, C, D, and H) contain repeated patterns of intervals (shown with dotted brackets). These intervallic repetitions are best described as patterns of diatonic intervals—counting steps on the staff, or on the major or minor scale—rather than chromatic ones (though diatonic intervals may match chromatically as well); for example, in Figure 1D, the first interval is a minor second in m. 1 and a major second in m. 2, but both represent a diatonic interval of +1. In all of these cases, the rhythm is repeated along with the pitch and/or interval pattern. In other cases, only the rhythmic pattern is repeated (shown with slurs); F and J are the most notable examples, though there are smaller rhythmic repetitions in other themes. Still other kinds of repetition could be cited. In E, one might argue that mm. 3–4 are an elaborated repetition of mm. 1–2; in F, one could point to the similarity in melodic contour (down-up) between mm. 2, 3, and 4. (There is sometimes more than one way of demarcating and labeling repeated patterns, as I will discuss below.) Thus, all ten of the themes arguably contain some form of pattern repetition. Though this sample is small and arbitrarily chosen, it gives a sense of the pervasiveness of pattern repetition in Western music, and the many ways in which it can occur.
Pattern repetition in music has been explored from a variety of perspectives. In music theory and analysis, the identification of short repeated patterns ("motives") has long been a central concern; Schoenberg (1950), Meyer (1973), Nattiez (1990), and Frisch (1990) are among the many prominent theorists who have focused on it. In music psychology, pattern repetition has been of interest for several reasons. Repeated patterns play an important role in the perception of meter, and efforts have been made to incorporate this factor into meter-finding models (Steedman, 1977; Lerdahl & Jackendoff, 1983; Vos, van Dijk, & Schomaker, 1994; Temperley & Bartlette, 2003). Pattern repetition may inform melodic segmentation (Cambouropoulos, 2006); it may also affect melodic expectation, a phenomenon captured by the "short-term" component of Pearce and Wiggins's IDyOM model (2006). In the field of music information retrieval, some attention has been given to pattern identification (Dannenberg & Hu, 2003; Lartillot & Toivianen, 2007), though the greater focus has been on the repetition of patterns across pieces rather than within them, as a way of characterizing musical styles or classifying pieces by style (Rolland, 1999; Conklin & Anagnostopoulou, 2006; Gulati et al., 2014; Arronte Alvarez & Gomez, 2021).

Figure 1. Themes from Barlow & Morgenstern (1948). Solid brackets show repeated pitch patterns; dashed brackets show repeated intervallic patterns; slurs show repeated rhythmic patterns. (A) Adolphe Adam, La Poupée de Nuremberg, overture, 1st theme; (B) Isaac Albéniz, Suite Española, "Cadiz," 1st theme; (C) Hugo Alfvén, Midsommarvarka, 1st theme; (D) Anton Arensky, Suite No. 1, I, 1st theme; (E) Kurt Atterberg, Symphony No. 6, I, 1st theme; (F) Daniel Auber, Le Cheval de Bronze, Overture, 1st theme; (G) Louis Aubert, Habañera, 1st theme; (H) Georges Auric, Les Matelots, 1st theme; (I) Johann Christian Bach, Concerto Op. 7 No. 1, I; (J) Johann Sebastian Bach, The Art of Fugue. *The last interval of the last measure differs from previous measures.
Another function of repeated patterns is that they allow melodies to be encoded more efficiently. In a classic experimental study by Deutsch (1980), listeners (musicians) were played short melodies and asked to write them down; some of the melodies were constructed from repeated patterns (like Figure 2A, featuring a three-note intervallic pattern) and some were not (like Figure 2B). The patterned melodies were transcribed much more accurately than the unpatterned ones, indicating that they were learned more easily. This shows both that listeners spontaneously identify repeated patterns, and that they use such repetitions to encode melodies parsimoniously—a form of data compression. As Deutsch shows, once a repeated pattern is identified, it need only be represented in memory once; an encoding of the melody can then indicate where the pattern occurs with "pointers" to its memory representation. These points are nicely illustrated by the melodies in Figure 1; we notice the repeated patterns effortlessly and automatically, and they make the melodies easy to learn and remember.
The ease with which we perform melodic pattern identification is all the more remarkable when we consider that it is, in fact, a highly complex and computationally intensive task. It involves comparing the current melodic segment to a potentially huge number of previous segments, finding earlier occurrences of the pattern and encoding the current segment accordingly. As we have seen, also, pattern similarity may take different forms: segments may match in exact pitch, in melodic interval, or in rhythm alone. (Looser forms of similarity—elaborated repetition and contour similarity—complicate the problem still further; in the current study I limit my attention to exact repetitions of pitch, diatonic interval, and/or rhythm.) I will argue here, however, that composers facilitate this encoding process by using repetition in highly constrained and systematic ways, simplifying the listener's search and aiding their creation of a parsimonious encoding.
More specifically, I present three hypotheses:
Hypothesis 1. Repeated intervallic patterns tend to be metrically parallel: occurrences of the pattern tend to be similarly placed in relation to the metrical structure.
Hypothesis 2. Purely intervallic repetitions tend to occur at short distances; longer-distance repetitions tend to involve repetition of scale-degrees as well.
Hypothesis 3. Repeated intervallic patterns tend to involve multiple intervals; isolated intervallic repetitions are not favored.
In what follows, I test each of these three hypotheses using statistical corpus analyses. My main focus is on European music of the common-practice period. I first discuss the corpora that I use and my procedure for analyzing them. I then turn to the three hypotheses, explaining the motivation for each one in relation to encoding efficiency and then testing it. I also briefly consider the three hypotheses with regard to rock music. In the final section, I discuss some further issues and possible directions for future research.
MATERIALS AND PROCEDURE
Materials
The main corpora used in this study are the Essen Folksong Collection and the Barlow & Morgenstern corpus. The Essen Folksong Collection is a corpus of 6,208 European folk songs containing a total of about 300,000 notes. It was created by Helmut Schaffrath (1991) and encoded in kern format by David Huron. 2 The vast majority of the songs are German, or at least have German-language titles, though there are a small number from other nations. Most of the songs were taken from published 19th-century collections. Some may question the use of the term "folksong," in this case or in general. The term tends to imply songs that are anonymous and passed down by oral tradition. In fact, most of the songs in the Essen corpus were taken by 19th-century collectors from earlier published collections; many of them had identified composers; some were taken from polyphonic compositions (Gelbart, 2007; Loges, 2012; Grosch, 2013; Brinkman, 2020). We can say, in any case, that the collection represents one aspect of musical practice in German-speaking areas of Europe during the 18th and 19th centuries.
The Barlow & Morgenstern (hereafter B&M) corpus contains the melodies in Harold Barlow and Sam Morgenstern's Dictionary of Musical Themes (1948), encoded on computer by David Huron in kern format. The corpus contains 9,788 melodic themes (about 200,000 notes), all from instrumental pieces; most are opening themes, but the corpus also includes a significant number of other themes, such as second themes from sonata movements. Most are from the 18th and 19th centuries; fewer than 1 percent predate 1700; roughly 20 percent of them are from after 1900, though many of these are by conservative composers (e.g., Rachmaninoff and Respighi) whose style might well be described as common-practice. A wide range of nations is represented, nearly all European; 41.9% of the themes are by German or Austrian composers. Taken together, the B&M and Essen corpora could be taken as providing a picture of compositional practice in Europe during the common-practice era, though with a bias toward German music in both corpora. (Even a true folk song was composed by someone—or by multiple people—whether they are identified or not.)
Representation Formats
Testing of the hypotheses stated above requires the identification of repeated melodic patterns and their alignment with the meter. To facilitate this, I converted the original kern format of the B&M and Essen corpora into two other formats. First I created what I call a "notestring" representation; see Figure 3A. In this notation, each measure in a melody is represented as a series of small, evenly spaced metrical units ("beats"), with vertical bars indicating barlines. (The format is essentially the same as that used in Temperley and de Clercq's [2013] study of rock music.) Every measure in a melody must contain the same number of beats, except perhaps the first and last measures. For each melody, a number of beats was chosen such that every note-onset coincided with a beat. Each beat has either a note symbol, if there is a note-onset there, or a dot, indicating either a rest or the continuation of a note. Note symbols represent each note as a scale-degree—a pitch-class in relation to the key. Scale-degree labels respect enharmonic distinctions; for example, b3 (Eb in the key of C) is distinguished from #2 (D#). Each note is assumed to be the closest possible representative of that scale-degree (in pitch height) to the previous pitch, unless marked with "^" (meaning an octave higher) or "v" (an octave lower). A note a tritone away from the previous pitch is assumed to be ascending unless marked with "v". The key is specified at the beginning of the melody. Scale-degree symbols always assume the major scale; E is 3 in either C major or C minor. The octave of the first note is also indicated, using the usual convention; for example, the pitch D4 is in octave 4. Given this information, the pitch of the first note can be identified and every subsequent note can be inductively identified from the previous one.
A second kind of representation, which I call a repetition representation, takes a notestring as input and indicates relationships between current beats and previous beats at a given rhythmic distance D. D is specified in relation to the measure; if D=1.0, each beat (metrical position) is compared to the beat exactly one measure earlier (the "comparison beat"). Figure 3B shows this representation for the melody in Figure 3A, assuming D=1.0. The figure shows first the notestring, then the same notestring shifted to align with itself at a distance of one measure, and then the repetition representation. The symbols in the repetition representation correspond to beats, but a symbol is only shown if the beat contains a note or the comparison beat contains a note (or both). A beat whose comparison beat is before the first note of the piece receives no symbol. Subsequent beats are then marked in the following way:
N: the current beat contains a note; the comparison beat does not
X: the comparison beat contains a note; the current beat does not
P/I/R/Z: both the current and comparison beats contain notes (we say the current note is "parallel" at distance D):
P: the two notes have the same pitch and are approached by the same diatonic interval ("pitch-intervallic repetition")
I: the two notes are approached by the same diatonic interval but differ in pitch ("intervallic-only repetition")
R: the two notes are approached by different diatonic intervals ("rhythmic-only repetition")
Z: the comparison note is the first note of the piece; therefore there is no interval to compare with the current note

Figure 3. (A) Hugo Alfvén, "Midsommarvarka," 1st theme, showing notestring representation and metrical grid. (B) The same notestring representation aligned with itself at a distance of one measure, with the repetition representation shown below.
Diatonic intervals can be computed from the notestring representation by looking only at the numbers in the scale-degree labels: for example, b2–b3, b2–3, 2–3, and #2–3 are all a diatonic interval of +1; 2–^3 is a diatonic interval of +8.
The repetition representation assumes a particular distance at which repetition occurs. One could take a melody and create multiple repetition representations for different distances (as we will). 3 Generally we will use distances corresponding to levels of the metrical structure; thus two beats being compared will be similar in metrical position. However, one could also examine repetition at distances that conflict with the meter; for example, in a melody in 4/4, one could examine repetition at a distance of 7/8. In this case, a note would be (for example) an I if there was another note approached by the same interval (but different in pitch) at a distance of seven eighth-notes earlier.
Identifying Repeated Patterns
While the repetition representation directly represents pairs of events, we can also use it to identify longer patterns. A series of parallel notes (P, I, R, or Z) in the repetition representation indicates a melodic segment that rhythmically repeats a previous segment: Two melodic segments whose corresponding notes are all separated by the same distance will also have the same durations, except perhaps for their final notes. (Here we define a note's duration as its "inter-onset interval," the rhythmic interval between its onset and the next note onset.) This can be confirmed in Figure 3B; the symbols "R I R" in the third measure indicate that it has the same rhythm as the second measure. A series of R's indicates purely rhythmic repetition; I and P indicate intervallic repetition as well. Thus, the repetition representation only shows patterns of pitch or intervallic repetition that also involve rhythmic repetition. It may be noted that defining a P as a repetition of both pitch and interval is somewhat redundant; if a segment contains several notes whose pitches match those of a previous segment, the intervals approaching the notes must match as well (with the exception of the first note). 4 However, it generally seems intuitive to regard pitch repetition as a special case of intervallic repetition; the current system facilitates this, allowing us to define intervallic repetitions as a category including both I's and P's.
A subtle point arises here regarding the conventional concept of "motive." Figure 4 shows the opening melody of Haydn's String Quartet Op. 33 No. 5; it features a clear repeated motive at a distance of two measures (marked by brackets). In informal terms, one might say that the motive is defined by six notes with specific durations and by the diatonic intervals between the notes (0 +1 +1 0 0). Notice that this definition excludes the diatonic interval approaching the first note of the motive. In the first instance of the motive, the first note is approached by +2 (G4–B4), while in the second instance it is approached by –3 (D5–
A4); yet it seems clear that this note is part of the motive. Using the symbols proposed above, and assuming a distance of two measures, the second instance of the motive would be represented as "R I I I I I." In general, I propose that salient intervallic motives consist of an R followed by one or more I's or P's. In Figure 1, the two-note motives shown in Themes C, G, and I all fit this description. (In Theme A, the first note of the motive is a Z; in Theme B, it is an I.) The first note of a motive might happen to be an I or P rather than an R, but this is not usually important to the identity of the motive. This way of defining motives is attractive from a cognitive point of view, because it means that an instance of a motive can be identified without regard to its intervallic context; the interval to the first note of the motive is unimportant. By this view, the duration of the last note of a motive is unimportant to its identity as well, since a note's duration does not affect its symbol in the repetition representation. Thus, motives are self-contained patterns of interval and duration. There is evidence that composers thought of motives in this way as well: Following a non-parallel event (N or X), sequences of multiple I's are much less common than an R followed by I's. For example, at a distance of 1.0 in the B&M corpus, following an N or X, the pattern "R I I" is 2.7 times more frequent than "I I I". The current view also implies that a single I or P, with "non-parallel" symbols (N or X) on either side, does not really count as a "motive"; if the interval to the first note in an intervallic motive is not part of its definition, then a pattern that consists only of a single interval has nothing to define it.
These considerations lead to the following definitions:
(1) A melodic segment (a series of two or more consecutive notes) is parallel to a previous segment if the two segments have the same number of notes and the corresponding notes in the two segments are all separated by the same distance. We may also say, equivalently, that the two segments are parallel to each other.
(2) A repeated intervallic pattern is a pair of parallel segments whose corresponding notes are approached by the same diatonic intervals (except that the intervals to the first notes of the segments need not match).
My use of the term "parallel" to describe motivic repetition follows Lerdahl and Jackendoff (1983), but I define it more precisely: I use the term to denote rhythmic repetition, and it always refers to a pair of segments. A given segment may be parallel to multiple previous segments at different distances. If a segment is parallel to a previous segment at distance D, each of its notes will be marked by R, I, P, or Z in the repetition representation (assuming a distance of D). A repeated intervallic pattern is also a pair of segments, matching not only in rhythm but in interval. In terms of the repetition representation, a repeated intervallic pattern is a series of two or more I's or P's (at some distance), though the first I or P may be replaced by an R or Z. If a pattern occurs more than twice, each pair of instances of the pattern constitutes a repeated intervallic pattern.
Finally, we must quantify the relationship between motivic repetition and meter. Here it is useful to invoke the well-known concept of the metrical grid: a framework containing several levels of evenly spaced beats. In Figure 3A, the metrical grid for the melody is shown above the staff, with levels for the half-note (the measure in this case), quarter-note, eighth-note, and sixteenth-note. The figure also shows two levels above the measure—"hypermetrical" levels, with beats on every second or fourth downbeat. (Hypermeter is nearly always duple, though there may be disagreement as to how high it extends.) Each metrical level is associated with a certain rhythmic distance—the distance between consecutive beats at that level; we call these the metrical distances for the piece. It is assumed that the metrical grid is uniform and unchanging throughout the piece, and that every note coincides with a beat in the grid. We now define metrical parallelism, a special case of parallelism as defined in (1) above:
(3) Two parallel segments are strongly metrically parallel if the distance between them is a metrical distance DM; they are weakly metrically parallel if they are not strongly metrically parallel and the distance between them is a multiple of a metrical distance DM. In both cases, the length of each segment—from its first note-onset to its last—must be less than DM.
| Distance (in measures) | CR | CI | CP | CI+P/CI+P+R (IRP)2 | CP/CI+P |
|---|---|---|---|---|---|
| B&M | |||||
| 0.25 | 17,909 | 5,906 | 1,460 | .291 | .198 |
| 0.5 | 16,442 | 5,569 | 1,624 | .304 | .226 |
| 1.0 | 12,984 | 4,902 | 1,829 | .341 | .272 |
| 2.0 | 6,805 | 3,068 | 1,558 | .405 | .337 |
| 4.0 | 989 | 389 | 209 | .377 | .349 |
| 7/8 (.875) | 9,885 | 2,091 | 379 | .200 | .153 |
| 9/8 (1.125) | 8,397 | 1,855 | 316 | .205 | .146 |
| Essen | |||||
| 0.25 | 28,845 | 8,615 | 2,468 | .278 | .223 |
| 0.5 | 30,172 | 8,763 | 1,466 | .253 | .143 |
| 1.0 | 29,714 | 7,970 | 1,917 | .250 | .194 |
| 2.0 | 26,380 | 8,698 | 3,973 | .324 | .314 |
| 4.0 | 18,741 | 5,827 | 7,418 | .414 | .560 |
| 8.0 | 10,183 | 3,095 | 2,729 | .364 | .469 |
| 7/8 (.875) | 13,988 | 3,029 | 645 | .208 | .176 |
| 9/8 (1.125) | 13,643 | 3,031 | 568 | .209 | .158 |
Note. 1C values indicate counts of different types of symbols in the repetition representation: P = repeated pitch and diatonic interval, I = repeated diatonic interval only, R = different diatonic interval.
2Intervallic Repetition Preference.
Another way to think about this may also be useful. The metrical grid forms a repeating pattern; two segments are metrically parallel if their corresponding notes are at the same positions in relation to the metrical pattern, up to some level. They are strongly metrically parallel if they inhabit consecutive parts of the grid at that level; they are weakly metrically parallel if they inhabit non-consecutive parts. Figure 3A shows some examples (consider the segments marked with brackets below the staff). Segments a and b fall at the same position with respect to the half-note level, and inhabit consecutive half-note parts of the grid, so they are strongly metrically parallel (DM = 1.0). Segments a and c are strongly metrically parallel at the two-measure level. Segments b and d are not strongly metrically parallel (the distance between them, 3.0, is not a metrical distance); they are weakly parallel at the half-note level, since 3.0 is a multiple of 1.0. Segments e and f are not even weakly metrically parallel; while the distance between them (3/8) is a multiple of a metrical distance (DM = 1/8), the length of the pattern exceeds this distance. The purpose of the length requirement is simply to limit the definition of metrical parallelism in a way that accords with intuition; without it, any two segments with the same rhythm would be weakly metrically parallel at the lowest metrical level.
Motivic Repetition in the Two Corpora
Using the conceptual framework presented above, Table 1 shows an initial analysis of the corpus data that will facilitate testing of the three hypotheses. For present purposes, it is most convenient to limit our attention to melodies in 4/4 time. This yields 2,364 melodies in the B&M corpus and 1,235 in the Essen corpus. Table 1 shows, for both corpora, the counts of various different symbols in the repetition representation, for different distances values. C values indicate the count for a particular symbol: CP is the count of P, and CI + P = CI + CP. Distances of 0.25, 0.5, and 1.0 are metrical distances—corresponding to levels of the 4/4 meter; distances of 2.0, 4.0, and 8.0 could be regarded as metrical as well, assuming duple hypermeter, though some might question whether these levels are always present, especially the 8-measure level. (The B&M corpus offers almost no data at the 8-measure level, since very few of the themes are that long.) The table also shows values for two non-metrical distances: 7/8 and 9/8. While the table only represents individual events, we can draw inferences from it about larger patterns, as I will explain.
HYPOTHESIS 1: THE PREFERENCE FOR MOTIVIC REPETITIONS AT METRICAL DISTANCES
We now address the first of our three hypotheses, which I earlier stated as follows: "Repeated intervallic patterns tend to be metrically parallel: occurrences of the pattern tend to be similarly placed in relation to the metrical structure." Using the terms defined above, we can now state the hypothesis more precisely and succinctly:
Hypothesis 1 (final version): Over short distances (within a few measures), repeated intervallic patterns tend to be strongly metrically parallel.
Another way of stating the hypothesis would be to say that the two segments of a repeated intervallic pattern are usually separated by a metrical distance. An intervallic pattern might occur many times, forming many pairs whose distances might sometimes be quite long and non-metrical (e.g. the return of the main theme in a sonata movement). The qualifier "over short distances" clarifies that the hypothesis applies to fairly local repetitions; the prediction is that the distances of such local repetitions will tend to be metrical. Figure 1 offers an informal test of this hypothesis. It can be seen that nearly all of the repeated intervallic patterns shown in the example are strongly metrically parallel. Themes A, C, G, H, and I have repeated intervallic patterns at the half-note level, and D and H at the whole-note level; B and I have such patterns at the quarter-note level, and C has one at the two-whole-note level.
Do the themes in Figure 1 contain any repeated intervallic patterns that are weakly metrically parallel or non-metrically parallel? One might point to the connection between measures 1 and 4 in theme D. This is a repeated intervallic pattern (overlooking the last note in measure 4); the two segments are three whole-notes apart, which is not a metrical distance in this piece. However, measure 4 is strongly metrically parallel to measure 3 at the whole-note level; so measure 4's intervallic pattern is at least strongly metrically parallel to some previous instance of the pattern. (One could phrase Hypothesis 1 a bit more strongly to state that, if a segment acts as the second segment of one or more repeated intervallic patterns, at least one of those patterns will be strongly metrically parallel; I will not pursue that here.) Consider also, in theme F, the ascending step D–Eb in measure 1 and the ascending step A–Bb in measure 2. This is a repeated intervallic pattern at a distance of 3/4; this is not a metrical distance, so the two instances of the pattern are not strongly metrically parallel. We cannot even say that they are weakly parallel at the quarter-note level, because the length of the pattern (one quarter-note) is not less than the metrical distance (1/4). Thus, Figure 1 does contain some counterexamples to the hypothesis; but the hypothesis does not state that repeated intervallic patterns are always strongly metrically parallel, only that they usually are.
In part, Hypothesis 1 is motivated simply by informal observations—like those above—that repeated intervallic patterns are common at metrical distances and rare elsewhere. But there are other motivations for it as well. It has been observed that the same melody presented in two different metrical contexts can sound like two completely different melodies (Sloboda, 1983; Povel & Essens, 1985; Temperley, 1995); the connection between them is difficult to to hear, suggesting that a pattern presented in different metrical contexts within the same piece may be difficult to hear as well. A recent study by Acevedo et al. (2014) confirms this experimentally: melodies with repeated patterns like those in Deutsch's experiment (e.g. Figure 2A) are learned more easily if instances of the pattern are presented in a context that makes them metrically parallel. Again, Figure 1 is illustrative: To my ears, the non-metrically-parallel ascending step in Theme F seems much less noticeable than the metrically parallel descending step in Theme C. However, the fact that listeners find non-metrically-parallel intervallic repetitions difficult to hear does not prove that composers avoid writing them; it is possible that music is full of such repetitions that escape our notice.
To examine this possibility, let us turn to the corpus data (Table 1). Recall that the symbols P, I, and R indicate a note that is preceded by another note at the defined distance (a "parallel note"); P or I means that the two notes are approached by the same diatonic interval; R means they are not. If repeated intervallic patterns tend to be strongly metrically parallel, then P's and I's—the building blocks of repeated intervallic patterns—should be higher in frequency at metrical distances than non-metrical ones. A particularly useful comparison is between the metrical distance 1.0 and the non-metrical distances 7/8 and 9/8, since all three are similar in terms of absolute time. We see, indeed, that in both corpora, the counts of I and P are much higher for 1.0 than for 7/8 and 9/8. However—if we take these results to indicate an intentional strategy on XX
the part of composers—there is a possible confound here: the difference in counts might be due simply to the fact that there are more parallel events overall at a distance of 1.0, including non-intervallic repetitions. And indeed, the count of R (non-intervallic repetitions) is also higher for 1.0 than for 7/8 and 9/8. (This is an interesting phenomenon as well, but not our present concern; I will return to it later in the article.) To measure intentional intervallic repetition, a more meaningful measure is the count of I and P as a proportion of all parallel events: This is represented in the table as CI+P/CI+P+R. Let us call this the "intervallic repetition preference" value (IRP) for that distance. 5 We see that this value is much higher for 1.0 than for 7/8 or 9/8, both in the B&M corpus and the Essen corpus (though less so in the latter); the differences between 1.0 and the two irregular meters in the proportional frequency CI+P+R are highly significant (B&M: 1.0 vs. 7/8, 𝒳2(1) = 742.58; 1.0 vs. 9/8, 𝒳2(1) = 612.33; Essen: 1.0 vs. 7/8, 𝒳2(1) = 116.99; 1.0 vs. 9/8, 𝒳2(1) = 110.9; p < 10-16 in all cases). This suggests—as predicted by the hypothesis—that intervallic repetitions are more common at metrical distances than at non-metrical ones, and that this does not arise simply from a preference for rhythmic repetition at metrical distances.
While the IRP values for 7/8 and 9/8 are relatively low, one might wonder if they still indicate some intentional use of intervallic repetition at these distances. Some repetition of intervals would occur just by chance, even if it were unintended—but how much? This can be roughly estimated by simply looking at the overall distribution of diatonic intervals in the corpus (again limiting ourselves to melodies in 4/4), squaring each value in the distribution, and summing those squares. This tells us how likely it is that two intervals randomly drawn from the corpus will match each other. This produces a value of .173 for the B&M corpus. The observed IRP values for the five metrical distances range from .291 to .405, suggesting a use of intervallic repetition much greater than chance. By contrast, the IRP values for distances of 7/8 (.200) and 9/8 (.205) are only slightly higher than would be expected by chance—closer to the chance estimate than to the observed values for metrical distances. (One-way chi-squares show that all IRP values—for both metrical and non-metrical distances—are significantly different from an expected proportion of .173, p < 10/15 in all cases.) For the Essen corpus, the chance value is .199; the observed values for metrically parallel distances are again much higher (p < 10-16 in all cases), while the values for 7/8 (.208) and 9/8 (.209) are barely above the chance estimate (though still significantly so, p < .01 in both cases). This suggests that there is very little intentional repetition of intervals at non-metrical distances. 6
Comparisons among the metrical distances are of interest as well. In general, the IRP value tends to be higher for higher metrical levels (longer distance values); it is highest for the 2-measure level in the B&M corpus and the 4-measure level in the Essen corpus. While the value for 0.25 is comparable to those at other levels, interval repetition at such a low level seems rather different in character from that at higher levels; often it simply involves the immediate repetition of a single interval, most often a step—a phenomenon known as "step inertia" (Huron, 2006)—or a unison (i.e. a pitch played three times in a row). In a case such as this, the repeated segment is just a single note, and thus (as I argued earlier) should not be regarded as an intervallic pattern. The same points would apply, even more strongly, to lower metrical levels (not shown in the table).
The current test looks only at parallelisms between individual notes, not between segments (intervallic patterns), but it seems clear that the trends observed for individual notes (I's and P's) would apply to patterns as well (repeated I's or P's): the data suggests that such patterns occur much more often at metrical distances than at non-metrical ones. 7 (As we will see in a later section, compositional practice shows a tendency to use I's and P's in "clusters" rather than in isolation.) And this relates directly to the issue of encoding. If intervallic patterns tend to occur at metrical distances, then listeners need only consider these distances in searching for repeated patterns as they seek an efficient encoding of the piece. Each current note must only be compared to a few previous notes, not all of them.
Again, Hypothesis 1 does not claim that repeated intervallic patterns are always strongly metrically parallel, or even that intentional, perceptible repeated patterns always are; such claims would clearly be too strong. Figure 5 shows a case in point, from Schubert's "Unfinished" Symphony; the parallelism between the first two notes and the last two is surely intentional and seems quite readily perceptible. These segments are separated by a distance of three measures, and thus not strongly metrically parallel; they are weakly metrically parallel at the 1-measure level. The conditions that favor the creation (and perception) of such repetitions are interesting to consider, but I will not explore that here. In a long piece, one may notice pattern repetitions at great distances that are presumably only weakly metrically parallel; I will say more about such long-distance connections in the next section.
One possibility that has not yet been considered is repetition of pitch or intervallic patterns between segments that differ in rhythm (durational pattern). By the current definitions, such segments could not be parallel (let alone metrically parallel), because the notes that they contain are not all parallel at the same distance; some notes might be parallel at metrical distances, others at non-metrical distances. The frequency of intervallic, non-rhythmic repetitions is difficult to test without a specific hypothesis as to how they might occur, but it seems unlikely that they are common. We have seen that repeated intervallic patterns that have the same rhythm but are non-metrically parallel are rare; surely two segments that were not even alike in rhythm would be even less favored. In Deutsch's 1980 study, discussed previously, it was found that disrupting the rhythmic similarity between intervallic repetitions greatly hindered people's ability to encode them efficiently. This is not to say that two segments must be rhythmically identical for any connection between them to be perceived; segments can have varying degrees of rhythmic similarity (Monahan & Carterette, 1985; Prince, 2014). Whether rhythmic similarity can facilitate encoding, in the way that exact rhythmic repetition does, has not been studied, to my knowledge.
HYPOTHESIS 2: PITCH VERSUS INTERVALLIC REPETITION
So far, we have generally lumped together pitch-intervallic repetition (P) and intervallic-only repetition (I), considering them both to be kinds of intervallic repetition. It is also of interest to examine them separately. To this end, we can take the values for 7/8 and 9/8 in Table 1 as rough chance estimates, showing the amount of pitch-intervallic repetition and intervallic-only repetition that would occur if no intervallic repetition of any kind was intended. (This seems justified by the tests presented above, showing that the overall amount of intervallic repetition at these distances—indicated by the IRP values—is close to a chance estimate.) For example, for the B&M corpus, consider CI / CR for 7/8 (.212) and for 1.0 (.378) (these ratios are not shown in the table). The fact that the ratio is much higher for 1.0 than for 7/8 suggests a clear preference to use intervallic-only repetition at metrical distances over non-metrical ones. Regarding pitch-intervallic repetition, the CP / CR ratios for 7/8 (.038) and 1.0 (.141) show an even more striking difference, suggesting that the preference for using such repetition at metrical distances is even stronger than for intervallic-only repetition.
These tests show that both intervallic-only repetition and pitch-intervallic repetition reflect a preference for metrical distances. However, there is a significant difference between these types of repetition in how they are used. This brings us to our second hypothesis, restated here:
Hypothesis 2: Purely intervallic repetitions tend to occur at short distances; longer-distance repetitions tend to involve repetition of pitch as well.
Hypothesis 2 is motivated, in part, by work in music psychology, especially that of Dowling and colleagues (Dowling, 1978; Dowling & Bartlett, 1981; Dowling & Harwood, 1986). These researchers have explored the way listeners encode familiar melodies and novel melodies being heard for the first time; they propose that different systems are used in these two situations. Familiar melodies, they suggest, are stored as patterns of scale-degrees (what they call "chromas"); this allows us to recognize a melody like "Happy Birthday" in different keys. But when a new melody is being heard, we are more sensitive to the intervals between notes. In experiments where listeners hear a novel, short melody followed immediately by a tonal transposition (which preserves diatonic intervals but not chromatic ones—what we have called a "repeated intervallic pattern"), they tend to report that the tonal transposition is "the same" as the original. This happens even when the difference between exact transposition and tonal transposition has been explained to them and they have been asked to judge only exact transpositions as the same. 8 In one sense, of course, two segments related by tonal transposition are the same—they feature the same pattern of diatonic intervals—and listeners seem to be sensitive to this; Deutsch's 1980 study, mentioned earlier, suggests this as well.

Figure 6. Stimuli from Dowling & Bartlett (1981). The figure is reproduced from Dowling & Harwood (1986).
One experiment by Dowling and Bartlett (1981) is of particular interest. In this experiment, listeners heard four melodic segments; they had to compare the third segment to the second (the "inside pair") and the fourth to the first (the "outside pair"). Each pair could be related by exact transposition or tonal transposition or could be completely different. Figure 6 shows one of their stimuli; in this case, the inside pair is related by exact transposition, the outside pair by tonal transposition. As usual, listeners had to judge whether the second melody in each pair was the same as the first—"the same" meaning an exact transposition. For the inside pair, both exact and tonal transpositions tended to be judged as the same; for the outside pair, however, tonal transpositions were judged as the same significantly less often than exact transpositions. This seems to suggest that as the earlier part of a melody recedes in time, it is converted into something more like a "long-term memory" format: the notes are stored as scale-degrees only, not intervals. Novel melodic segments are then compared to those scale-degree segments; the new and old segments must match in scale-degrees for a match to be found.
It seems clear that matching a new melodic segment to one stored in memory—either short-term or long-term—is affected by the metrical similarity between the two segments (i.e. their placement in relation to the metrical context). In the case of short-term memory, a repeated melodic pattern is encoded more easily if successive instances of the pattern are similarly aligned with the meter (Acevedo et al., 2014); with regard to long-term memory, Creel (2011) shows that the encoding of a melody incorporates the metrical context in which it was first heard. Thus, over both short and long temporal intervals, the perception of repetition is affected by metrical context. Even so, there is an important difference between encoding a melodic segment in some kind of long-term library (call this a "library encoding") and encoding it as part of a complete encoding of the current musical context, along with its exact distance from the current segment (call this a "contextual encoding"). The encoding of familiar melodies (allowing us to match a new melody to one we have heard before) is clearly a library encoding. Recognizing strong metrical parallelism—which depends on the distance between the current segment and a previous one—would require a contextual encoding. Even within a hearing of a single long piece, though, our encoding may become more like a library encoding as segments recede in time. Imagine hearing a sonata-form movement for the first time; the recapitulation begins and we recognize the return of the opening theme. We surely have not encoded the entire piece up to that point; perhaps we have encoded only certain motivic ideas that were emphasized earlier (e.g. by repetition or formal placement). Nor does our recognition of the theme depend on the exact distance between its first occurrence and the current one. At intermediate distances (say four or eight measures) our encoding may be transitional between a contextual encoding and a library encoding: We may retain much of what we have heard, along with exact distances, but we begin to lose interval information, encoding the notes only as scale-degrees.
If listeners are more sensitive to scale-degree repetition than to purely intervallic repetition over long distances, one might wonder if this preference is reflected in compositional practice. We can examine this issue using the B&M and Essen corpora. The use of pitch-intervallic repetition in itself tells us little, since it preserves both scale-degrees and diatonic intervals; but if the frequency of exact repetitions relative to tonal transpositions (preserving only diatonic intervals) increases as distance increases, that will suggest that the compositional preference for scale-degree similarity relative to intervallic-only similarity increases with distance. 9 In Table 1, CP / CI+P indicates pitch-intervallic repetitions as a proportion of all intervallic repetitions. It can be seen, as predicted, that this value increases steadily as distance increases. In the B&M corpus, this pattern is completely consistent from level to level. Each time the metrical distance doubles, CP / CI+P appears to increase by a roughly constant amount; that is, the increase in CP / CI+P is approximately linear with the logarithm of the metrical distance. The correlation between CP / CI+P and log(distance) is strong and significant (r = .98, p < .01). The same general pattern is seen in the Essen corpus, with two exceptions. First, 0.25 has a higher CP / CI+P ratio than 0.5; probably this is due to the fact that a single pitch is often repeated several times in a row. The other exception is that the ratio decreases slightly from the four-measure level to the eight-measure level; for this, I have no explanation. However, the ratio for eight measures is still much higher than that for two measures and shorter distances. The correlation between CP / CI+P and log(distance) is somewhat lower than in the B&M corpus, but still high and significant (r = .84, p < .05).
Thus, corpus data is consistent with the idea that long-term memory representations of melodies use scale-degrees rather than intervals. It remains to be explained why this memory strategy is used. Clearly it would not be efficient for listeners to represent melodies in long-term memory with both intervals and scale-degrees; this would place an onerous burden on memory. (For short-term memory, where only a small amount of music is being encoded, the burden is much less.) In a sense, a scale-degree representation is more robust than an intervallic one; if one note in an intervallic representation is encoded incorrectly, the entire remainder of the melody will be off. In any case, once this listening strategy is assumed, it is clearly helpful to the encoding process for composers to favor scale-degree repetitions over intervallic-only repetitions at longer distances.
HYPOTHESIS 3: REPEATED SEGMENTS VERSUS INDIVIDUAL NOTES
I have repeatedly spoken of repeated patterns in melodies. But the repetition representation—the basis for all the conclusions drawn so far—does not explicitly show patterns (repeated segments); it only shows individual notes in relation to previous notes. With regard to the issue of efficient encoding, this is an important distinction. Suppose we identify a single note as an "I" at a distance of one measure: for example, a note on the downbeat approached by an interval of +1. We could encode this note as a motive, M1, and substitute M1 in our representation of the melody every time such an note occurs. This does not seem much more efficient than simply representing the interval directly; we are simply substituting one symbol for another. By contrast, if we notice, say, four I's in a row, and encode the entire pattern as M1, the gain in efficiency is much more evident.
This is not to say that isolated repeated intervals (I's or P's) are not recognized as repetitions. They may well be in some cases—though I have suggested that a single I or P must be preceded by a metrically parallel note (R) in order to be perceptually salient. Several of the patterns marked in Figure 1—the two-note patterns in Themes A, C, G, and I— involve just "R I" or "R P." Even a pattern such as this does not contribute much to efficient encoding (though one might say that the R aids in the encoding of rhythm). On the other hand, one might say that recognizing such short patterns is a necessary intermediate step in recognizing longer ones. In any case, it seems clear that—with or without a preceding R—longer clusters of I's and P's are more beneficial to encoding than shorter ones. A preference for longer patterns is also reflected in most computational pattern-finding models (Meek & Birmingham, 2001; Dannenberg & Hu, 2003; Lartillot & Toivianen, 2007).
Composers could facilitate efficient encoding by favoring clusters of I's or P's, rather than just sprinkling them haphazardly through the music. This motivates our third hypothesis:
Hypothesis 3: Repeated intervallic patterns tend to involve multiple intervals; isolated intervallic repetitions are not favored.
To test this hypothesis, we must once again devise a chance estimate. Let us treat each of the two corpora as a single long stream of symbols: R, I, P, Z, N, or X. We can then examine how much clustering of I's and P's would occur if symbols were randomly and independently generated, preserving the overall distribution of symbols that we observe in the corpus. In the B&M corpus, assuming D=1.0, .122 of symbols are I's (call this value PI) and .045 of symbols are P's (PP). (Here we use the entire corpus, not just melodies in 4/4 time,
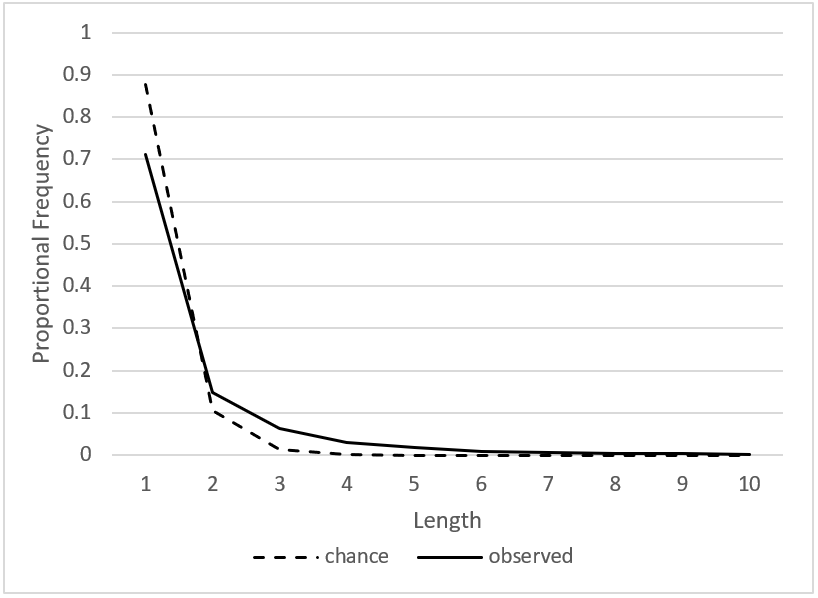
Figure 7. Proportional frequency of sequences of intervallic-only repetitions of different lengths in the B&M corpus, observed and chance.
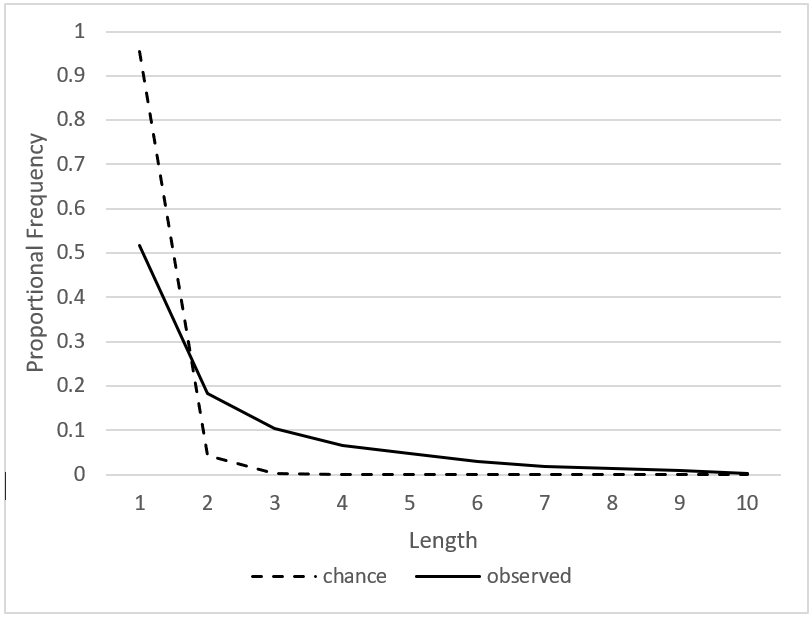
Figure 8. Proportional frequency of sequences of pitch-intervallic repetitions of different lengths in the B&M corpus, observed and chance.
though we exclude melodies with irregular or changing time signatures.) Beginning with I, we consider sequences of I's (with something other than I on either end) of different lengths, and the frequency of sequences of each length that would occur due to chance. The expected frequency of a sequence of length L is proportional to (PI)L. 10 We calculate this for all values of L up to 30; for higher values of L, (PI)L is so small as to be negligible. We add the (PI)L values together, and then divide each (PI)L by this sum, so that it represents a proportion of the total. The resulting values for each sequence length up to 10 are shown by the dotted line in Figure 7. The solid line shows the observed proportional counts of sequences of I's of different lengths. It can be seen that clusters of I's (with length greater than 1) occur somewhat more often than would be expected due to chance (𝒳2 (1) = 3290, p < 10-16). Figure 8 shows the same values for pitch-intervallic repetitions; in this case, the preference for clusters is much greater (𝒳2 (1) = 3923.6, p < 10-16). For both I's and P's, sequences of length 1 are still most common, but they are less common than would be expected by chance. The Essen corpus shows very similar patterns (not shown here). Once again, the relevance of this to the encoding process is clear. By clustering repeated intervals together, composers allow several repeated intervals to be represented with a single symbol, thus facilitating the creation of an efficient encoding.
MOTIVIC REPETITION IN ROCK MUSIC
One might wonder how much the conclusions drawn here would apply to other musical styles. As a first step in that direction, let us consider a third corpus: the Rolling Stone corpus, which contains rock melodies from approximately 1955 to 2000 (Temperley & de Clercq, 2013). Here we use a subset of the corpus, a set of 80 melodies (25,774 notes) that has been used elsewhere (Tan, Lustig, & Temperley, 2019), all in 4/4 time, roughly evenly balanced between the five decades (the 1950s through the 1990s). While this corpus contains far fewer melodies than the B&M and Essen corpora, the melodies are much longer: The Rolling Stone corpus contains 322 notes per melody on average, versus 19 in the B&M corpus and 47 in the Essen corpus. The melodies are in "notestring" format in their original form, facilitating their use here. Table 2 shows all of the tests applied earlier to the B&M and Essen corpora. The CI+P/CI+P+M values are much higher for metrical distances than for non-metrical ones; comparing the value for 1.0 with those for 7/8 and 9/8 yields highly significant differences (1.0 vs. 7/8: 𝒳2(1) = 127.63, p < 10-16; 1.0 vs 9/8: 𝒳2(1) = 136.07, p < 10-16). This shows, as with the other corpora, that intervallic repetitions tend to occur at metrical distances. A chance estimate of intervallic repetition yields a value of .205, similar to chance estimates for the other two corpora.
Of particular interest is CP/CI+P, showing the preference for pitch-intervallic repetition as a proportion of all intervallic repetition. I have suggested elsewhere (Temperley, 2018, 96–7), based on informal observation, that intervallic-only repetition is much less frequently used in rock than in common-practice music; this may be because it is often unclear in rock songs what the "scale" is and how notes should be assigned to diatonic-scale categories. In Figure 9A, for example, the starred notes in the pick-up and the first measure would usually be regarded as D#'s—chromatic lower neighbors to 3—but the one in the second measure seems more like a b3, reflecting the major/minor mixture typical of rock. (Even the assignment of notes to chromatic scale categories can be difficult in rock, due to the use of "blue notes.") The data in Table 2 confirm my observation. At all metrical distances, a large proportion of intervallic repetitions (sometimes more than half) are pitch repetitions—much larger than the corresponding proportions in the B&M and Essen corpora (see Table 1). I suspect that even these values overestimate the true amount of intentional intervallic repetition in rock. Inspecting the data, many apparent cases of intervallic repetition simply involve two segments in which a pitch is repeated several times; the bracketed segments in Figure 9B are a case in point. In such cases it seems questionable that any intervallic repetition is intended. More convincing intervallic repetitions do occur (Figure 9C shows one) but they are not common. Investigating these issues in other musical styles—especially non-Western styles—would be an obvious area for further research.
DISCUSSION
The current study has shown three regularities in common-practice melodic composition that aid the process of creating an efficient encoding. First, intervallic repetitions tend to occur at metrical distances; this means that, in finding patterns of repetition between a current segment and previous ones, listeners need only
| Distance (in measures) | CM | CI | CP | CI+P/CI+P+M | CP/CI+P |
|---|---|---|---|---|---|
| 0.25 | 8,456 | 1,506 | 2,175 | .303 | .591 |
| 0.5 | 7,447 | 1,447 | 1,432 | .281 | .492 |
| 1.0 | 6,974 | 1,645 | 1,570 | .316 | .488 |
| 2.0 | 7,502 | 1,965 | 2,932 | .395 | .599 |
| 4.0 | 6,706 | 1,737 | 4,221 | .470 | .708 |
| 8.0 | 6,425 | 1,621 | 2,535 | .393 | .610 |
| 7/8 (.875) | 6,927 | 1,386 | 889 | .247 | .391 |
| 9/8 (1.125) | 6,752 | 1,394 | 731 | .239 | .344 |

Figure 9. (A) Bachman-Turner Overdrive, "Takin' Care of Business." (B) Bruce Springsteen, "Born to Run." (C) Michael Jackson, "Billie Jean."
consider earlier segments at a few distances from the current segment. Second, composers tend to confine intervallic-only repetitions to short distances, favoring repetitions that preserve scale-degree at longer distances; this fits well with listeners' apparent preference for scale-degree repetition when matching segments over longer distances. Finally, composers tend to use intervallic repetitions in clusters (especially pitch-intervallic repetitions); this allows several consecutive intervals to be encoded as a single repeated pattern, which is more efficient than encoding a single interval in this way.
Our focus throughout the study has been on intervallic repetitions, either combined with pitch repetition or not. But as mentioned with regard to Figure 1, there is also the possibility of purely rhythmic repetition. This does not aid encoding in quite the same way as intervallic repetition, because it does not specify pitch, but it can be seen that it might facilitate the encoding of rhythm itself. One might wonder if we could examine the use of repeated rhythmic patterns as we did with intervallic patterns. To do this, we could collapse the categories R, Z, I, and P (each representing a note with a preceding note at a distance of D) into one category M; we would then distinguish only between parallel notes (M), notes matched by a preceding non-note (N), and non-notes matched by a preceding note (X); we might then predict that M's would occur more often at metrical than non-metrical distances. A problem arises here, however. With intervallic patterns, we have assumed that the pitch of a note and the interval to it are more or less independent of the note's metrical position, so that repetition of intervals or scale-degrees at metrical distances can generally be viewed as intentional. While this independence assumption is not strictly true, correlations between metrical position and interval or scale-degree are small, and taking them into account does not significantly change the chance
estimates presented earlier (see note 5). With rhythm, the situation is quite different: there are very strong correlations between metrical position and note status (note vs. no note), with notes being much more probable at strong metrical positions (Palmer & Krumhansl, 1990; Huron, 2006). If rhythmic repetition is more common at metrical distances—notes are more often matched by notes, and non-notes by non-notes—this may be largely because notes are more likely to occur at certain metrical positions. Chance estimates of rhythmic repetition would have to be of quite a different character from those proposed earlier for intervallic repetition; this would take us in a different direction that I will not pursue here.
Throughout this study, it has been assumed that music listening involves an active process of searching for repeated patterns. I have touched on various aspects of this process, but have not provided a concrete account of how it works. Modeling musical pattern identification has been the subject of several previous studies, and has proven to be very difficult problem (Meek & Birmingham, 2001; Meredith et al., 2002; Dannenberg & Hu, 2003; Lartillot & Toiviainen, 2007). A piece will generally contain a huge number of possible patterns, many of them redundant with one another; the challenge is to identify those that are perceptually significant. Pattern recognition models, such as those cited above, generally incorporate preferences for longer patterns (reflected also in my Hypothesis 3), more specific patterns (e.g. those that involve interval and rhythm as opposed to rhythm alone), and those that occur more often. All three of these preferences have clear benefits for efficient encoding. The current study has suggested some additional constraints or preferences: We favor metrically parallel patterns, and we favor scale-degree repetition over intervallic repetition at longer distances. But even with these constraints, there may be many possible ways of analyzing a section of music. For example, Figure 1C contains a two-note pitch pattern that occurs twice (mm. 3-4), a two-note intervallic pattern that occurs three times (mm. 2, 3, and 4), and a three-note rhythmic (and contour) pattern that occurs three times (mm. 2, 3, and 4): the choice between these encodings depends on how the preferences for long patterns, specific patterns, and frequent patterns are weighed against one another. Looser forms of similarity, such as elaborated repetition and contour repetition, must also be taken into account—a problem addressed by some computational and experimental studies (Mont-Reynaud & Goldstein, 1985; Boltz & Jones, 1986; Rolland, 1999)—though how these kinds of inexact repetition contribute to efficient encoding is less clear. Altogether, much work remains to be done in the modeling of musical pattern identification.
The current study raises a deeper issue as well, regarding the relationship between composition and perception. With regard to all three of the hypotheses posed above, I have suggested that regularities of composition are well-suited to strategies of perception and processing. I have implied, also, that this is a result of compositional practice responding to perception. Composers use repeated patterns at metrical distances because listeners look for them there; they favor scale-degree repetition over intervallic repetition at long distances because listeners do; they use repeated intervals in clusters because this helps encoding. But there may also be a process of perception responding to composition: perhaps, for example, listeners don't look for repeated patterns at non-metrical distances because composers don't use repeated patterns in that way. Or perhaps (indeed, very likely), a more complex process of back-and-forth influence between composition and perception is at work. In my view, arguments regarding ease of encoding make a compelling case for composition responding to perception. It seems clear that encoding is easier if intervallic repetitions are limited to certain distances; it is not clear why this would make composing easier. Still, the causal relationship between composition and perception, with regard to these phenomena, remains an open question, one that should be borne in mind in future studies of pattern repetition in music.
ACKNOWLEDGMENTS
I am grateful to David Huron for making available his encoding of the Barlow & Morgenstern corpus in kern notation. This article was copyedited by Matthew Moore and layout edited by Jonathan Tang
NOTES
-
Correspondence can be addressed to: David Temperley, Eastman School of Music, 26 Gibbs St., Rochester, NY 14604, USA. Email: dtemperley@esm.rochester.edu
Return to Text -
The corpus is publicly available at <https://kern.humdrum.org/cgi-bin/browse?l=essen/europa>.
Return to Text -
The repetition representation has precedents in earlier studies that propose ways of measuring a piece of music's "self-similarity" at different distances, sometimes using the technique of autocorrelation. Generally this method is used for the purpose of identifying meter (Brown, 1993; Vos et al., 1994; Temperley & Bartlette, 2003), or for identifying repeated patterns in audio (Aucouturier & Sandler, 2002); I know of nothing similar to the representation that I propose here.
Return to Text -
The only exception to this would be if one of the notes was the same pitch in the two pattern instances but spelled differently; for example, in C major, C–Eb followed by C–D#. In that case, pitches would match but not diatonic intervals (+2 in the first case, +1 in the second). Notice also that it is very unlikely for an I and a P to occur adjacently. This would imply that there were two pairs of adjacent notes, N1-N2 and N3-N4, each note pair separated by the same diatonic interval, where the first (or second) notes of each pair matched in pitch and the other two pitches did not. This could only occur in the unusal case where the two non-matching pitches had the same diatonic scale-degree (e.g., in C major, C4-E4 and C4-Eb4).
Return to Text -
A preliminary version of this test was presented in Temperley (2014). There, as here, I examined the proportion of parallel notes that were also intervallic repetitions, at various different distances, using 4/4 melodies in the B&M corpus as data. However, I did not compare to chance estimates, as I do here. Another precedent for the current test is seen in a study by Vos et al. (1994), who examine intervallic repetition using autocorrelation (essentially similar to what I do here). They find high autocorrelation values for distances corresponding to metrical levels in the unaccompanied works of Bach. However, they only consider chromatic intervals, not diatonic ones, which I suspect causes the amount of intervallic repetition to be greatly underestimated.
Return to Text -
The current argument assumes that there is no correlation between metrical position and approaching interval. If there were—for example, if downbeat notes tended to be approached by a certain interval—then a high IRP for metrical distances might arise simply because of that. Inspection of interval distributions at different positions suggests that there may be, at least, small correlations of this kind; for example, metrically stronger positions seem more likely to be approached by leap—an interesting phenomenon in itself that we will not explore here. (There are also modest correlations between metrical position and scale-degree; see Prince and Schmuckler, 2014.) A more rigorous chance estimate would consider the interval distributions at different metrical positions, and would weight each metrical position according to the proportion of parallel notes that occur there (which might be different for different distances). Chance estimates of this kind were calculated for the B&M 4/4 corpus for distances of 1.0 and 7/8, and they were almost identical to the ones presented above: .172 for 1.0 and .173 for 7/8.
Return to Text -
I said earlier that an isolated I or P—not part of a larger parallel segment—does not usually seem to constitute a significant motive. From a compositional perspective, then, we would not expect isolated metrically parallel notes to show strong intervallic repetition tendencies. It was also noted that it is more common for a repeated intervallic pattern to begin with an R rather than with an I or P. Taking both observations into account, we might say that we do not predict a metrically parallel note that follows an N or X to be an I or P rather than an R. Indeed, in the B&M corpus, at a distance of 1.0, the probability of a parallel note following an N or X being an I or P is just .191—barely higher than the chance estimate, .173. If such notes are excluded from the test shown in Table 1 (for the B&M corpus at a distance of 1.0), the IRP value increases to .440.
Return to Text -
It is possible that listeners in these experiments were encoding tonal transpositions in an incomplete or approximate way—perhaps only as contour patterns; Dowling and Harwood seem to suggest this (1986, 134–6). We should note, though, that Dowling and colleagues are inconsistent in their use of the term "contour," sometimes interpreting it to mean "diatonic interval pattern." (See e.g. Dowling, 1978, 348.) In any case, I strongly suspect that listeners are able to recognize repeated diatonic interval patterns (not just contours) in novel melodies. A diatonic interval pattern uniquely specifies pitches (at least if a diatonic scale is assumed), but a contour pattern does not; thus contour patterns do not contribute to efficient encoding in the same way that diatonic interval patterns do. A contour-based account therefore has difficulty explaining the results of Deutsch's 1980 study (discussed earlier) and the evident ease of learning and reproducing melodies with repeated diatonic interval patterns such as Figure 1D. (For an opposing viewpoint, see Boltz & Jones, 1986.) Listeners' inability to distinguish between tonal and exact transposition in Dowling's experiments may be due, not to a failure to encode the melodies precisely, but rather, to the difficulty of bringing this distinction to conscious awareness.
Return to Text -
Dowling and Barlett's experiment used exact transpositions (shifting a melody from one key to another), not exact pitch repetitions, but pitch repetition could be regarded as a special case of exact transposition; both preserve scale-degrees. If listeners generally judge exact transpositions as "the same," they surely would do so for exact repetitions as well.
Return to Text -
More precisely: If we examined randomly generated data, and started a new cluster of I's each time an I occurred after a non-I, the probability of generating a cluster of I's of exactly length L would be (PI)L × (1–PI). The final term will be the same for all values of L, so if we are only interested in the relative probabilities of different cluster lengths, it can be disregarded.
Return to Text
REFERENCES
- Acevedo, S., Temperley, D., & Pfordresher, P. (2014). Effects of metrical encoding on melody recognition. Music Perception, 31, 372–386. https://doi.org/10.1525/mp.2014.31.4.372
- Arronte Alvarez, A., & Gómez, F. (2021). Motivic pattern classification of music audio signals combining residual and LSTM networks. International Journal of Interactive Multimedia and Artificial Intelligence, 6, 208–214. https://doi.org/10.9781/ijimai.2021.01.003
- Aucouturier, J., & Sandler, M. (2002). Finding repeating patterns in acoustic musical signals: Applications for audio thumbnailing. Proceedings of the Audio Engineering Society Conference: 22nd International Conference: Virtual, Synthetic, and Entertainment Audio. Audio Engineering Society.
- Barlow, H., & Morgenstern, S. (1948). A dictionary of musical themes. New York: Crown Publishers.
- Boltz, M., & Jones, M. (1986). Does rule recursion make melodies easier to reproduce? If not, what does? Cognitive Psychology, 18, 389–431. https://doi.org/10.1016/0010-0285(86)90005-8
- Brinkman, A. (2020). Exploring the structure of Germanic folksong. PhD Dissertation, Ohio State University.
- Brown, J. C. (1993). Determination of the meter of musical scores by autocorrelation. Journal of the Acoustical Society of America, 94, 1953–1957. https://doi.org/10.1121/1.407518
- Cambouropoulos, E. (2006). Musical parallelism and melodic segmentation: A computational approach. Music Perception, 23, 249–268. https://doi.org/10.1525/mp.2006.23.3.249
- Conklin, D., & Anagnostopoulou, C. (2006). Segmental pattern discovery in music. INFORMS Journal on Computing, 18, 285–293. https://doi.org/10.1287/ijoc.1040.0122
- Creel, S. (2011). Specific previous experience affects perception of harmony and meter. Journal of Experimental Psychology:Human Perception and Performance, 37, 1512–1526. https://doi.org/10.1037/a0023507
- Dannenberg, R., & Hu, N. (2003). Pattern discovery techniques for music audio. Journal of New Music Research, 32, 153–163. https://doi.org/10.1076/jnmr.32.2.153.16738
- Deutsch, D. (1980). The processing of structured and unstructured tonal sequences. Perception & Psychophysics, 28, 381–389. https://doi.org/10.3758/BF03204881
- Dowling, W. J. (1978). Scale and contour: Two components of a theory of melody for memories. Psychological Review, 85, 351–354. https://doi.org/10.1037/0033-295X.85.4.341
- Dowling, W. J., & Barlett, J. C. (1981). The importance of interval information in long-term memory for melodies. Psychomusicology, 1, 30–49. https://doi.org/10.1037/h0094275
- Dowling, W. J., & Harwood, D. L. (1986). Music cognition. San Diego: Academic Press.
- Frisch, W. (1990). Brahms and the principle of developing variation. Berkeley, CA: Univ of California Press.
- Gelbart, M. (2007). The invention of 'folk music' and 'art music': emerging categories from Ossian to Wagner. Cambridge: Cambridge University Press. https://doi.org/10.1017/CBO9780511481918
- Grosch, N.. (2013). The Old German Folksongs philological: Tracing a fake, 49, Muzikološki zbornik, 23–32.
- Gulati, S., Serra, J., Ishwar, V., & Serra, X. (2014). Mining melodic patterns in large audio collections of Indian art music. In 2014 Tenth International Conference on Signal-Image Technology and Internet-Based Systems (pp. 264–271). IEEE. https://doi.org/10.1109/SITIS.2014.73
- Huron, D. (2006). Sweet anticipation: Music and the psychology of expectation. Cambridge, MA: MIT Press. https://doi.org/10.7551/mitpress/6575.001.0001
- Lartillot, O., & Toiviainen, P. (2007). Motivic matching strategies for automated pattern extraction. Musicae Scientiae, 11, 281–314. https://doi.org/10.1177/102986490701100111
- Lerdahl, F., & Jackendoff, R. (1983). A generative theory of tonal music. Cambridge, MA: MIT Press. https://doi.org/10.7551/mitpress/12513.001.0001
- Loges, N. (2012). How to make a 'Volkslied': early models in the songs of Johannes Brahms. Music & Letters, 93, 316–349. https://doi.org/10.1093/ml/gcs036
- Meek, C., & Birmingham, W. (2001). Thematic extractor. Proceedings of the International Society for Music Information Retrieval.
- Meredith, D., Lemström, K., & Wiggins, G. (2002). Algorithms for discovering repeated patterns in multidimensional representations of polyphonic music. Journal of New Music Research, 31, 321–345. https://doi.org/10.1076/jnmr.31.4.321.14162
- Meyer, L. (1973). Explaining music. Berkeley, CA: University of California Press. https://doi.org/10.1525/9780520333109
- Monahan, C. B., & Carterette, E. C. (1985). Pitch and duration as determinants of musical space. Music Perception, 3, 1–32. https://doi.org/10.2307/40285320
- Mont-Reynaud, B., & Goldstein, M. (1985). On finding rhythmic patterns in musical lines. Proceedings of the International Computer Music Conference.
- Nattiez, J. J. (1990). Music and discourse: Toward a semiology of music. Princeton University Press.
- Palmer, C., & Krumhansl, C. (1990). Mental representations for musical meter. Journal of Experimental Psychology: Human Perception and Performance, 16, 728–741. https://doi.org/10.1037/0096-1523.16.4.728
- Pearce, M., & Wiggins, G. (2006). Expectation in melody: The influence of context and learning. Music Perception, 23, 377–405. https://doi.org/10.1525/mp.2006.23.5.377
- Povel, D., & Essens, P. (1985). Perception of temporal patterns. Music Perception, 4, 411–440. https://doi.org/10.2307/40285311
- Prince, J. (2014). Contributions of pitch contour, tonality, rhythm, and meter to melodic similarity. Journal of Experimental Psychology: Human Perception and Performance, 40, 2319–37. https://doi.org/10.1037/a0038010
- Prince, J., & Schmuckler, M. (2014). The tonal-metric hierarchy: A corpus analysis. Music Perception, 31, 254–70. https://doi.org/10.1525/mp.2014.31.3.254
- Rolland, P. Y. (1999). Discovering patterns in musical sequences. Journal of New Music Research, 28(4), 334–350. https://doi.org/10.1076/0929-8215(199912)28:04;1-O;FT334
- Schaffrath, H. (1991). Zum Einsatz von Computern in Musikwissenschaft und -pädagogik. In H. Schaffrath (ed)., Computer in der Musik (pp. 8–26). Berlin: Springer-Verlag. https://doi.org/10.1007/978-3-476-98901-7_1
- Schoenberg, A. (1950). Style and idea. New York: Philosophical Library.
- Sloboda, J. (1983): The communication of musical metre in piano performance. The Quarterly Journal of Experimental Psychology Section A: Human Experimental Psychology, 35, 377–396. https://doi.org/10.1080/14640748308402140
- Steedman, M. J. (1977). The perception of musical rhythm and metre. Perception, 6, 555–569. https://doi.org/10.1068/p060555
- Tan, I., Lustig, E., & Temperley, D. (2019). Anticipatory syncopation in rock: A corpus study. Music Perception, 36, 353–70. https://doi.org/10.1525/mp.2019.36.4.353
- Temperley, D. (1995). Motivic perception and modularity. Music Perception, 13, 141–169. https://doi.org/10.2307/40285692
- Temperley, D. (2014). Information flow and repetition in music. Journal of Music Theory, 58, 155–178. https://doi.org/10.1215/00222909-2781759
- Temperley, D. (2018). The musical language of rock. New York: Oxford University Press. https://doi.org/10.1093/oso/9780190653774.001.0001
- Temperley, D., & Bartlette, C. (2003). Parallelism as a factor in metrical analysis. Music Perception, 20, 117–149. https://doi.org/10.1525/mp.2002.20.2.117
- Temperley, D., & de Clercq, T. (2013). Statistical analysis of harmony and melody in rock music. Journal of New Music Research, 42, 187–204. https://doi.org/10.1080/09298215.2013.788039
- Vos, P., van Dijk, A., & Schomaker, L. (1994). Melodic cues for metre. Perception, 23, 965–976. https://doi.org/10.1068/p230965




