NOTWITHSTANDING the recent proliferation of symbolic music corpora, the computational musicology community still lacks accessible and usable datasets for the quantitative study of tonal structure, harmony in particular. Notable contributions enabling the empirical study of harmony in common-practice European composition styles include manual analyses encoded in text (Tymoczko et al., 2019) or Excel files (Chen & Su, 2018), as well as symbolically encoded music scores with manual annotations by experts (Devaney et al., 2015; Nápoles López, 2017; Neuwirth et al., 2018; Hentschel, Moss, et al., 2021; Hentschel, Neuwirth, & Rohrmeier, 2021). 2 All these datasets adopt some variant of Roman-numeral-based syntax to ascribe harmonic meaning to specific pitch events. The chronological range they cover, however, is imbalanced towards the 18th and late 17th centuries; with the present contribution we address this bias by providing a new extensive corpus of annotated piano music that spans the long 19th century. 3
The timbral characteristics of the piano and the topology of its keyboard had a momentous effect on compositional practices during the dataset period (Samson, 2004), which consolidated the galant style's freer play with patterns of tonal motion exempt from the constraints of vocal music (Moseley, 2016). The long 19th century also marks long transitions away from classical diatonic tonality towards various expressions of "extended tonality" (Cohn, 1998; Polth, 2018; Rohrmeier & Moss, 2021). The result of a large-scale four-year annotation project, this dataset is an initial step toward larger chronological, geographical, and stylistic coverage of this highly eventful century.
METHOD
Scores
This dataset comprises 264 annotated scores encoded in the XML-based format of the free and open-source MuseScore 3 editor. Some of the scores have been newly engraved by our collaborators, others were downloaded from public domain repositories. Their pitch and rhythmic content has been checked for consistency with print editions that are in the public domain. 4 Online sources, reference editions, engravers (where known), and correctors are referenced in the metadata. All annotations and metadata are included or referenced within the MuseScore files for convenient inspection. 5 They are stored as uncompressed plaintext so that the history of all revisions by annotators and reviewers can be tracked using the git version control system (Swicegood, 2008).
Annotations
The annotations follow the DCML harmony annotation standard (Hentschel, Neuwirth, & Rohrmeier, 2021). Annotation labels were entered directly into the scores using the Roman numerals functionality of MuseScore 3. The labels represent complete harmonic analyses of each piece, including: the initial key (typically construed as global tonality), modulations, harmonic spans labeled as Roman numerals, phrase boundaries, and cadences. The labels were collaboratively created and reviewed by a pool of trained music theorists. The annotation standard consists of a set of annotation guidelines that annotators and reviewers adhere to, as well as a regular expression for validating the syntactical correctness of the labels. The present dataset uses the latest version of the standard (2.3.0), which differs from the version described in the Annotated Mozart Sonatas (Hentschel, Neuwirth, & Rohrmeier, 2021): among other improvements, cadence annotations are now integral to the harmony syntax and made directly on the symbolically encoded score, alongside Roman numeral annotations, thus obviating the use of special text files (see "ODD principle" below).
The present dataset is the first one entirely created through the semi-automated workflow proposed in Hentschel, Moss, et al., 2021, which we implemented using the GitHub data-hosting platform. 6 The workflow includes automated validity checks and is intended to contain the subjectivity inherent in this type of music analysis by enforcing a protocol of annotation verification by expert consensus. More specifically, every set of annotation labels, whether new or upgraded from an earlier version of the standard, has been reviewed by at least one additional annotator who acts as reviewer. Reviewers were tasked with committing their suggested edits in a separate version branch (i.e., GitHub pull request), thereupon requesting consent from the original annotator or upgrader to merge the edits into the main line. The latter reacts to the pull request by reviewing suggested changes. In cases of disagreement on a particular label or passage, the two collaborators enter a discussion in order to achieve a music-theoretically founded resolution, an exchange that may involve further iterative changes. Only at that point of consensus is the pull request merged. In the interest of accountability and transparency, the considerations of our annotators are captured, both indirectly in the revision history of each piece ("git diffs"), and directly in the form of prose discussions via GitHub.
THE DATASET
Composers and works
The dataset consists of 264 compositions of nine European composers for solo piano (see Figure 1 and Table 1): Beethoven's piano sonatas (complete); 55 Mazurkas by Chopin; Debussy's Suite Bergamasque, L. 75 (complete); Dvořák's Silhouettes, Op. 8; Grieg's Lyric Pieces (all opera, complete); Liszt's Années de Pèlerinage I & II (including the supplément to the latter); 19 of Medtner's Tales; Schumann's Kinderszenen, Op. 15 (complete); and Tchaikovsky's Seasons, Op. 37a (complete). Composition dates range from 1794 (Ludwig van Beethoven's Op. 2) to 1925 (Nikolai Medtner's Op. 48). The dataset contents have been selected according to the principle of unity in diversity. The selection exhibits a degree of intra-corpus unity: the works within each individual corpus comprise cycles (such as Robert Schumann's Kinderszenen, Op. 15) or sets of sonatas (in the case of Beethoven)—in whole or part. Each of the nine corpora has also been selected to introduce new textures, forms, genres, or styles to the dataset.
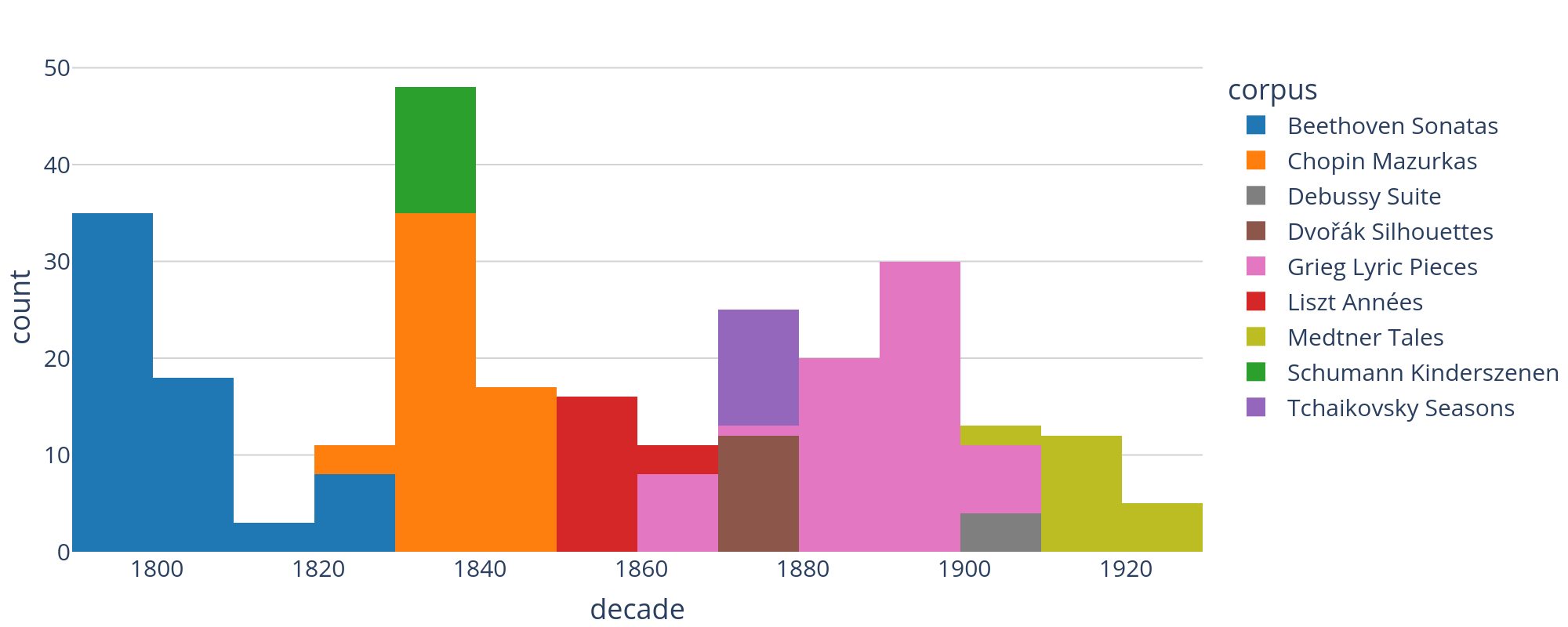
Figure 1. Histogram showing the number of annotated pieces for each of the nine corpora that are part of the dataset. The x-axis indicates the composition dates binned by decades.
| Absolute | Per Piece | Per Measure | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pieces | Measures | Length | Notes | Labels | Measures | Length | Notes | Labels | Notes | Labels | |
| Beethoven Sonatas | 64 | 11662 | 35663.38 | 165948 | 21962 | 182.22 | 557.24 | 2592.94 | 343.16 | 14.23 | 1.88 |
| Chopin Mazurkas | 55 | 5089 | 14605.25 | 57201 | 9127 | 92.53 | 265.55 | 1040.02 | 165.95 | 11.24 | 1.79 |
| Debussy Suite | 4 | 421 | 1616.00 | 8210 | 1013 | 105.25 | 404.0 | 2052.5 | 253.25 | 19.5 | 2.41 |
| Dvořák Silhouettes | 12 | 674 | 1852.50 | 10649 | 1539 | 56.17 | 154.38 | 887.42 | 128.25 | 15.8 | 2.28 |
| Grieg Lyrical Pieces | 66 | 5414 | 16485.25 | 65774 | 8231 | 82.03 | 249.78 | 996.58 | 124.71 | 12.15 | 1.52 |
| Liszt Années | 19 | 2625 | 9709.25 | 59534 | 5068 | 138.16 | 511.01 | 3133.37 | 266.74 | 22.68 | 1.93 |
| Medtner Tales | 19 | 2464 | 6598.00 | 42929 | 6730 | 129.68 | 347.26 | 2259.42 | 354.21 | 17.42 | 2.73 |
| Schumann Kinderszenen | 13 | 392 | 934.00 | 5223 | 948 | 30.15 | 71.85 | 401.77 | 72.92 | 13.32 | 2.42 |
| Tchaikovsky Seasons | 12 | 1250 | 3919.50 | 18751 | 3059 | 104.17 | 326.62 | 1562.58 | 254.92 | 15.0 | 2.45 |
| Sum | 264 | 29991 | 91383.13 | 434219 | 57806 | ||||||
Formats and features
The dataset follows an ODD (One Document Does it all) approach: the annotated MuseScore file may always be safely assumed to encapsulate the most up-to-date syntactically valid annotations to the piece in question, alongside all available metadata. The same information is additionally provided in the form of plaintext TSV-formatted feature tables for increased interoperability with other datasets and analysis tools. These files are automatically extracted from the annotated MuseScore (.mscx) files by the ms3 parsing library (Hentschel & Rohrmeier, 2023) as part of the aforementioned GitHub workflow, which at the same time computes additional columns for convenience, such as the offset of events from the beginning of the score, measured in quarter notes. The data facets that are extracted by default for each piece include:
- a measures table, summarizing important attributes of the XML-encoded measure units within the MuseScore files, such as time signatures, measure numbers, and repeat signs;
- a notes table, which represents all note heads in the score together with relevant features thereof;
- a harmonies table, which gathers features parsed from the actual annotations or computationally derived from them.
We refer users to the ms3 parser which provides relevant functionality in the form of packaged Python functions and command-line tools. Its documentation also includes in-depth information on the feature columns contained in the TSV files. In addition to the piece-specific tabular files, a metadata table is also generated and kept up to date for each corpus individually and for the dataset as a whole, compiling authorship and attribution information alongside composition and edition URIs. This metadata is likewise contained in and extracted from the MuseScore files. Our GitHub workflow also produces a set of interactive timeline plots which graphically depict the key areas, modulations, and tonicizations of each individual piece on the time axis.
Descriptive statistics
The figures and tables in this section are supposed to quantitatively characterize some of the main properties of the dataset and hint at a few differences between the nine included sets of compositions.
NOTES
Although the approximately 434.000 notes of the dataset stem from two-hand piano scores, in six pieces they are distributed over three (Grieg, Liszt, Medtner) or even four staves (Liszt's Sonetto 47 del Petrarca, S. 161, No. 4). Figure 2 aggregates for each corpus the total sounding durations of each piano key and shows the distributions as violin plots. The included rectangular boxes further indicate the pitch ranges on the piano keyboard where 50 % of the sound mass occurs, measured in musical time (quarter notes). The middle line indicates the median and dots on the fringes represent outliers whose distance from the box is above 1.5 times the interquartile range. All nine medians lie slightly above the middle C4, three corpora (Grieg, Liszt, and Medtner) have outliers on the lowest key of the modern piano keyboard (A0) and all corpora except Schumann and Tchaikovsky include pitches above C7. The latter two are also the ones with the smallest ambitus of 66 and 64 semitones, respectively.
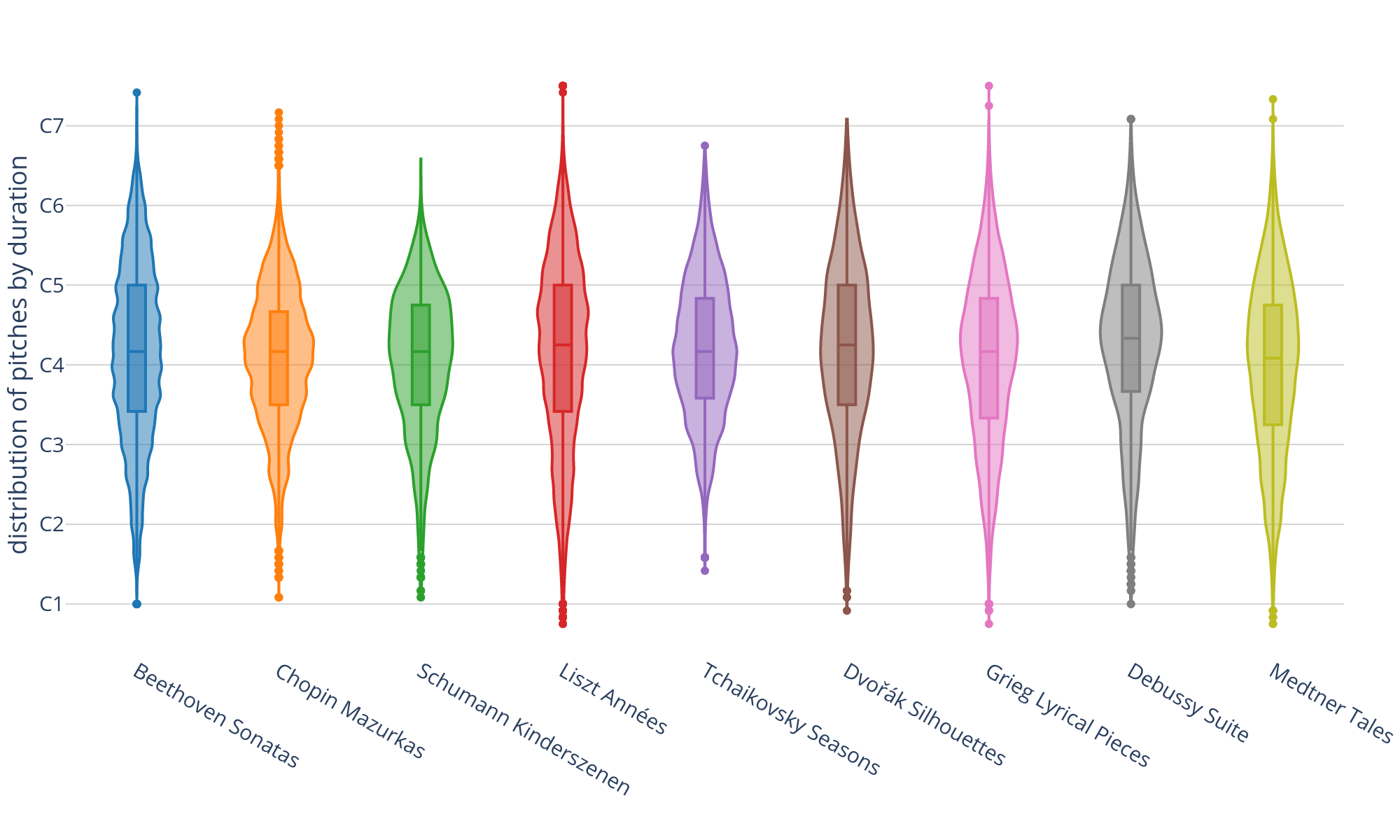
Figure 2. Violin and box plots showing the distribution of pitches for each corpus. Outliers exceeding 1.5 times the inter-quartile range are shown as points.

Figure 4. Line plots showing the distribution of aggregated and normalized durations of tonal pitch classes for each corpus, ordered on the line of fifths.
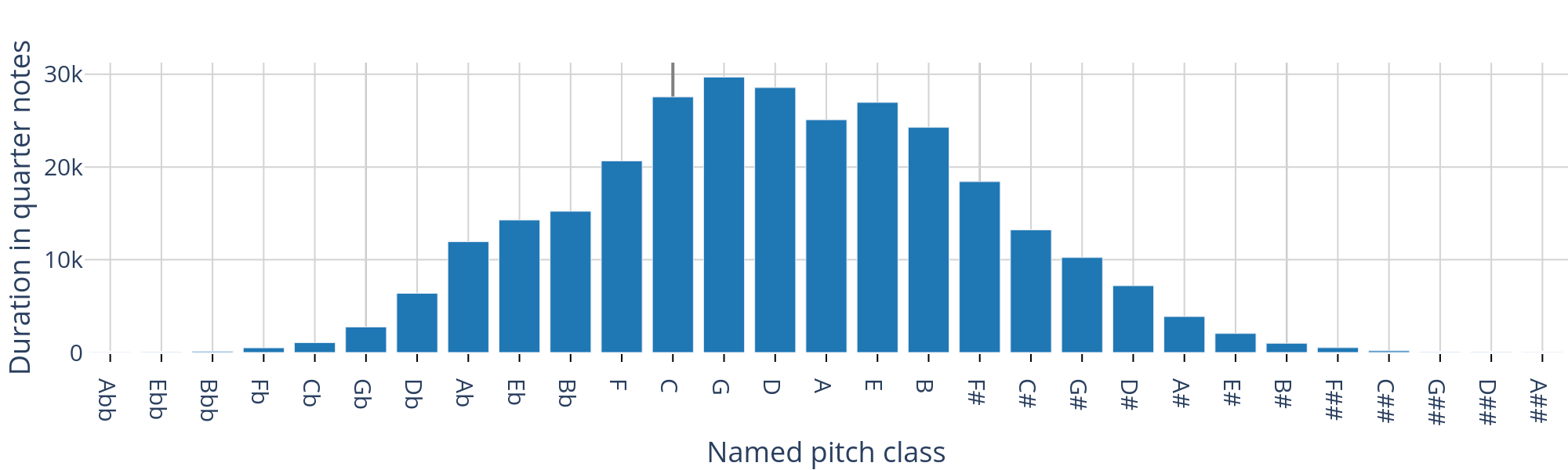
Figures 3 and 4 show the distributions of aggregated note durations over all pitch classes, ordered on the line of fifths. Roughly 62.6 % of the total duration of pitch classes have names without accidentals. The distribution of the individual corpora shows quite varied pitch class characteristics, with a tendency of smaller corpora to exhibit more local maxima.
PHRASES
The distribution of lengths shown in Figure 5 encompasses the roughly 3,600 phrases with unchanging meter, leaving out 52 phrases with one time-signature change, and one with two time-signature changes. This decision enables us to express length in number of measures rather than tactus units. Considering the logarithmic y-axis, the distribution shows two global peaks for the bins around 4 (n=859) and 8 (n=850) and local peaks at 12, 16, and 24.
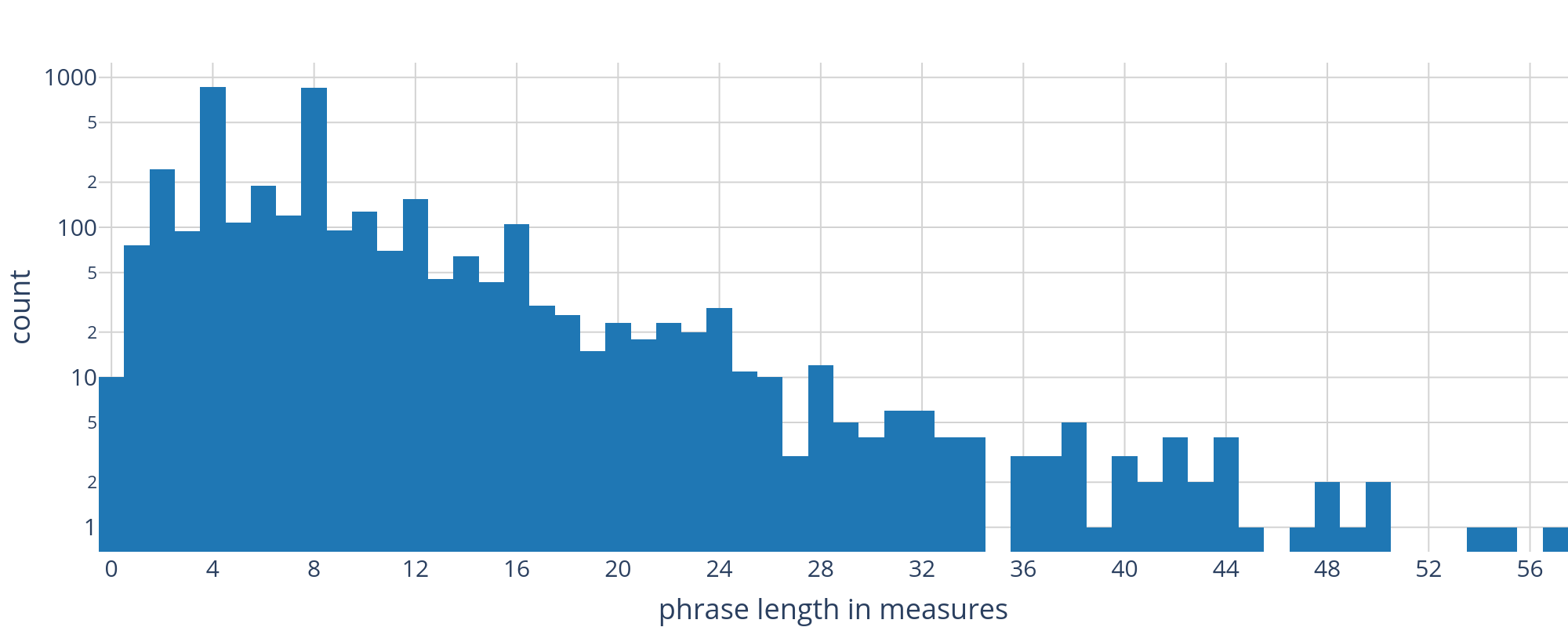
Figure 5. Histogram showing the length of each of the 3544 phrases, as determined and peer-reviewed by our annotators, with counts on the y-axis measured on a logarithmic scale. Lengths are counted in measures.
As the histogram suggests, several of these lengths are counterintuitively long and appear to contradict common form-theoretical notions of classical "phrase." Indeed, phrase-level groupings were determined by our human annotators, not algorithmically, and subjected to the same standardized peer-review process as the Roman numeral annotations. For the sake of consistency and integrity, we publish this phrase data as-is, with the proviso that it should be used either as statistical material for "distant reading," or otherwise with caution. To improve the quality of phrase data in the future, we are considering a revision to our workflow which would dedicate a separate peer-review phase entirely to that layer of the dataset.
KEY SEGMENTS
The bar plot in Figure 6 shows the distribution of local key areas relative to each piece's global tonic over the entire dataset. Expressing roots as intervals between the global to the local tonic allows us to compare the distribution of all key segments independently of the global key at hand. Considering the logarithmic y-axis, it becomes clear that the vast majority of the corpus music (roughly 73.6 % of its duration) is in the major or minor mode of the global tonic.

Figure 6. Distribution of local key segments over the dataset. Local-key tonics are expressed as intervals relative to the global tonic (P=perfect, M=major, m=minor, a=augmented, d=diminished). Segments in major mode are shown in blue, minor segments in orange. Durations are shown on a logarithmic scale and have been computed by aggregating the length in quarter notes of all segments in a given key.
CADENCES
The bar plot in Figure 7 is the only one expressing label counts rather than their durational extent. Cadence labels mark the time point where cadential closure is reached, often, but not necessarily, in conjunction with the chord indicating the final harmony (the ultima). Although they could theoretically be used for segmenting the music, the duration of the annotated cadences themselves are not specified. The counts alone, however, hint at major differences between the nine composers in their use of cadence as a compositional device. Consider, for example, the relatively high fraction of perfect authentic cadences in the Chopin's Mazurkas (nearly 60%), or the total absence of evaded cadences in three of the nine corpora (Tchaikovsky, Grieg, Medtner).
HARMONY LABELS
Figure 8 shows how the 56,755 chord label tokens (3,125 unique types) are distributed over the total duration of the dataset, grouped by chord roots. In order to represent all chords in one plot, we have reduced them to their root and chord type features (123 unique types), leaving out additional encoded features such as their inversion, suspensions, or other non-chord tones. Chord prevalence is shown on a logarithmic scale, indicating that only a very small part (0.4 %) of the corpus was analyzed as having roots on augmented or diminished scale degrees.
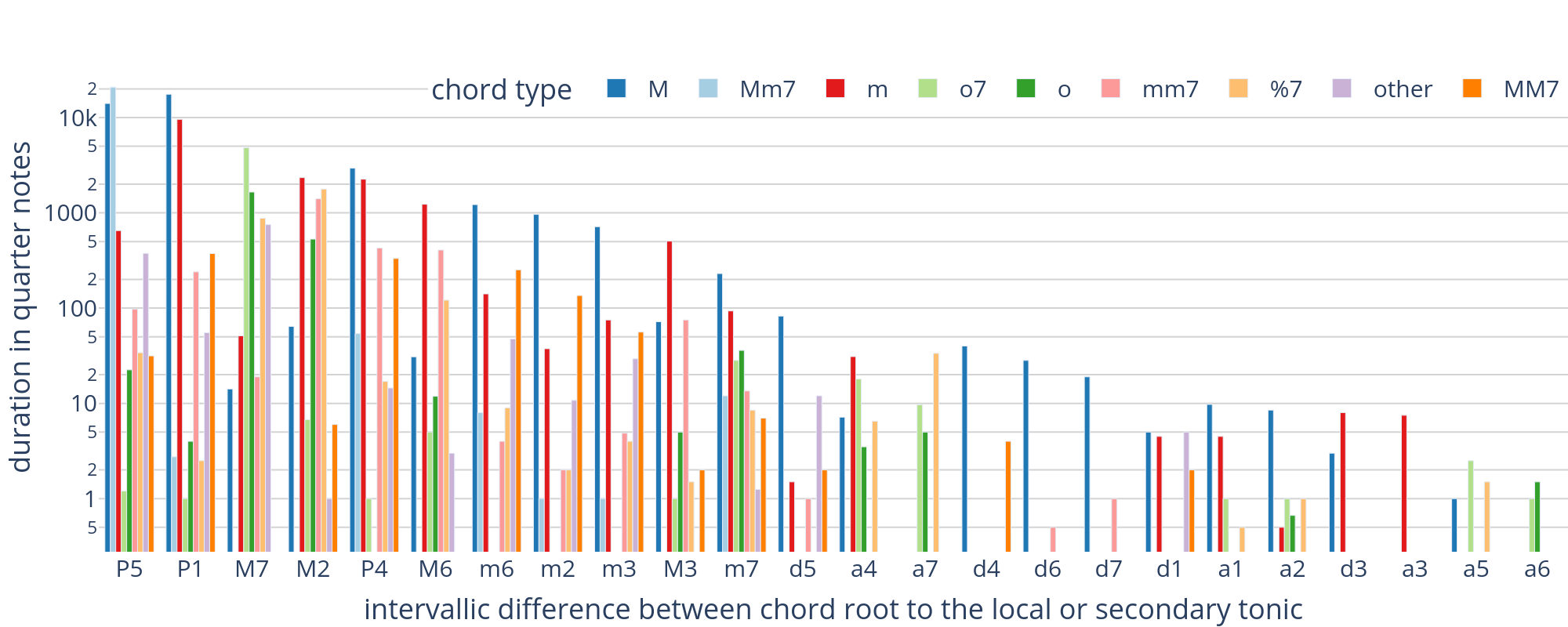
Figure 8. Bar plot showing the distribution of chord types over chord roots. The roots are expressed as intervals over the local tonic or, in the case of applied chords, over the tonicized key. For example, 'viio7/V' appears as 'M7', the scale degree of the leading tone. The chord types read as M=major triad, m=minor triad, o=diminished triad; m7=minor 7th; M7=major 7th; %7=half-diminished seventh chord. Interval labels on the horizontal axis are labeled as P (perfect), M (major), m (minor), a (augmented), or d (diminished).
DISCUSSION AND CONCLUSION
This data report presented an extensive corpus of 19th-century piano music, which contains digital scores, annotated harmony labels, phrases, and cadences. The corpus was created using the DCML harmony annotation standard (version 2.3.0). For quality assurance purposes we implemented the semi-automated workflow concept as outlined in Hentschel, Moss, et al., 2021. This workflow enables the production of peer-reviewed digitally encoded analyses, while also paving the way for further revisions in a principled and accountable fashion. The full revision history of the annotations is retained and potentially serves as a source of data for further empirical research on arguably under-researched topics, such as the evaluation of uncertainty in harmonic analysis and inter-annotator agreement (Koops et al., 2019).
While the 19th to 20th century piano repertoire is vast, our selection of 264 movements and ~57,560 labels is a major step towards addressing the paucity of music analysis corpora. Constrained by limited resources, we selected composers with notably distinct styles spanning the long 19th century, organizing a considerable diversity of forms and genres into single-composer corpora with a high degree of internal unity. While our selection of composers and works is far from exempt from "canon biases," we sought to counteract a 19th-century analogue to what Justin London (2013), in his study on representative classical-music corpora, described as "Mozart/Beethoven effect" in corpus building. To this end, we included composers who received significantly different frequency rankings in this study—for example Medtner, who is conspicuously absent from them.
Corpus representativeness remains an open, much-discussed challenge in digital musicology. The disjunction between histories of production (composition) and those of reception (performance, listening, criticism) further complicates the undertaking: a corpus considered representative of 19th-century harmony 130 years ago—therefore more "authentic" in a historicist sense—would likely be quite different from the present one, which rather reflects an expert assessment of the current 19th-century canon. Ultimately, the contents of this dataset reflect the consensus of a group of music theorists (including the authors) on questions of representativeness according to the following constraints: characteristic harmonic phenomena and piano textures from a contemporary listener's point of view, national coverage, financial resources available for commissioning annotations, and score availability.
The intra- and inter-corpus coverage leaves significant room for expansion towards composers of both established and emerging relevance in contemporary 19th–century music studies, including women and minority composers. A future dataset with stronger emphasis on late-style works would also be valuable—with the crucial proviso that this designation is widely construed as not chronological but more broadly biographical (Burnham, 2011; Straus, 2008), encompassing a constellation of features, both structural and expressive. Future corpus initiatives would also benefit from expansion towards more chromatic extended-tonality music (late Liszt, middle-period and late Scriabin, early Schoenberg, and others). With the momentum that the fields of music corpus research specifically, and digital musicology in general, have recently gathered, we are anticipating the publication of comparable datasets making use of open formats and FAIR principles. The "Special Issue on Open Science in Musicology" released in 2021 by the Empirical Musicology Review (Vol. 16 No. 1) is a notable case in point. Only by joining forces and resources can we prepare the ground for daunting musicological challenges, such as large-scale studies of music stylometry, or advanced empirical research on formal models of music structure—not to mention a wide range of MIR and music AI tasks which can benefit from the high-quality datasets emerging in the field.
END MATTER
Acknowledgements
This research was supported by the Swiss National Science Foundation within the project "Distant Listening – The Development of Harmony over Three Centuries (1700–2000)" (Grant no. 182811). This project is being conducted at the Latour Chair in Digital and Cognitive Musicology, generously funded by Mr. Claude Latour. This article was copyedited by Annaliese Micallef Grimaud and layout edited by Jonathan Tang.
Author Contributions
JH conceived the protocol and workflow toward the creation of this dataset, contributed reviews, developed the annotations parser, and implemented the semi-automated workflow. JH and YR contributed to this text in equal parts. FM, MN, and MR selected the corpora. JH, MN, and FM collected available encodings and commissioned missing encodings as well as the original set of annotations. JH and FM performed initial proof-reading of the analyses. JH and YR commissioned and oversaw later upgrades of the original labels. MR made this publication possible through longterm planning, acquisition of funds, and helpful guidance.
NOTES
-
Correspondence can be addressed to: Johannes Hentschel, EPFL-CDH-DHI-DCML, INN 115, Station N° 14, CH-1015 Lausanne, johannes.hentschel@epfl.ch.
Return to Text -
For a meta-initiative trying to bring these resources into a unified format, please refer to https://github.com/MarkGotham/When-in-Rome
Return to Text -
The "long 19th century" is a widely accepted historiographic trope generally referring to the period from the French Revolution to the First World War. Originating in early-20th-century literary-history writings, it gained currency thanks to Eric Hobsbawm's three-volume study of that period (e.g. Hobsbawm 1987). The productivity of the term in musicology is demonstrated by Richard Taruskin in his Oxford History of Western Music (vol. 4, chapter 8).
Return to Text -
The scores of the dataset do not adhere to Urtext edition standards; doing so would have multiplied the cost of the data collection by orders of magnitude, while the gained benefit for the use of computational, digital musicology and MIR research tasks may be limited.
Return to Text -
In this sense, we follow a one-document-does-it-all (ODD) approach, although data facets are made available in the form of separated values.
Return to Text -
That is without taking into account the annotated Sonate a tre by A. Corelli that were released together with the aforementioned workflow article.
Return to Text
REFERENCES
- Burnham, S. G. (2011). Late styles. In R.-M. Kok & L. Tunbridge (Eds.), Rethinking Schumann (pp. 411–430). Oxford University Press. https://doi.org/10.1093/acprof:oso/9780195393859.003.0018
- Chen, T.-P., & Su, L. (2018). Functional Harmony Recognition of Symbolic Music Data with Multi-Task Recurrent Neural Networks. 19th International Society for Music Information Retrieval Conference, 90–97.
- Cohn, R. (1998). Introduction to Neo-Riemannian Theory: A Survey and a Historical Perspective. Journal of Music Theory, 42(2), 167–180.
- Devaney, J., Arthur, C., Condit-Schultz, N., & Nisula, K. (2015). Theme and Variation Encodings with Roman Numerals (TAVERN): A New Data Set for Symbolic Music Analysis. 16th International Society for Music Information Retrieval Conference, 728–734.
- Hentschel, J., Moss, F. C., Neuwirth, M., & Rohrmeier, M. A. (2021). A semi-automated workflow paradigm for the distributed creation and curation of expert annotations. Proceedings of the 22nd International Society for Music Information Retrieval Conference, ISMIR, 262–269. https://doi.org/10.5281/ZENODO.5624417
- Hentschel, J., Neuwirth, M., & Rohrmeier, M. (2021). The Annotated Mozart Sonatas: Score, Harmony, and Cadence. Transactions of the International Society for Music Information Retrieval, 4(1), 67–80. https://doi.org/10.5334/tismir.63
- Hentschel, J., & Rohrmeier, M. (2023). ms3: A parser for MuseScore files, serving as data factory for annotated music corpora. Journal of Open Source Software, 8(88), 5195. https://doi.org/10.21105/joss.05195
- Hobsbawm, E. (1987). Age Of Empire: 1875-1914. Weidenfeld & Nicolson.
- Koops, H. V., Haas, W. B. de, Burgoyne, J. A., Bransen, J., Kent-Muller, A., & Volk, A. (2019). Annotator Subjectivity in Harmony Annotations of Popular Music. Journal of New Music Research, 48(3), 232–252. https://doi.org/10.1080/09298215.2019.1613436
- London, J. (2013). Building a Representative Corpus of Classical Music. Music Perception, 31(1), 68–90. https://doi.org/10.1525/mp.2013.31.1.68
- Moseley, R. (2016). Keys to Play: Music As a Ludic Medium from Apollo to Nintendo. University of California Press. https://doi.org/10.1525/luminos.16
- Nápoles López, N. (2017). Joseph Haydn—String Quartets Op.20—Harmonic Analysis Annotations Dataset [Data set]. Zenodo. https://doi.org/10.5281/ZENODO.1095630
- Neuwirth, M., Harasim, D., Moss, F. C., & Rohrmeier, M. (2018). The Annotated Beethoven Corpus (ABC): A Dataset of Harmonic Analyses of All Beethoven String Quartets. Frontiers in Digital Humanities, 5(July), 1–5. https://doi.org/10.3389/fdigh.2018.00016
- Polth, M. (2018). The Individual Tone and Musical Context in Albert Simon's Tonfeldtheorie. Music Theory Online, 24(4). https://doi.org/10.30535/mto.24.4.15
- Rohrmeier, M., & Moss, F. C. (2021). A Formal Model of Extended Tonal Harmony. Proceedings of the 22nd International Society for Music Information Retrieval Conference, ISMIR, 569–578.
- Samson, J. (2004). Virtuosity and the Musical Work: The Transcendental Studies of Liszt. Cambridge University Press. https://doi.org/10.1017/CBO9780511481963
- Straus, J. N. (2008). Disability and "Late Style" in Music. Journal of Musicology, 25(1), 3–45. https://doi.org/10.1525/jm.2008.25.1.3
- Swicegood, T. (2008). Pragmatic Version Control Using Git. The Pragmatic Bookself.
- Taruskin, R. (2005). The Oxford History of Western Music: The Nineteenth Century (Vol. 3). Oxford University Press.
- Tymoczko, D., Gotham, M., Cuthbert, M. S., & Ariza, C. (2019). The RomanText Format: A Flexible and Standard Method for Representing Roman Numeral Analyses. 20th International Society for Music Information Retrieval Conference, Delft, The Netherlands, 2019, 123-129.