TONAL functions—tonic, pre-dominant, and dominant—are a standard feature of North American music theory. The pre-dominant (PD) encompasses the largest number of chords, varying in quality and scale degrees; unlike the tonic and dominant functions, it is primarily defined by its syntactical role (Caplin, 1998; Guck, 1978; Nobile, 2016), directly preceding the arrival of the dominant function. Scholarly research on the PD is scant, save a seminal paper exploring the expansion of the function in music composed in the Romantic era (Stein, 1983) and a recent experiment on the perceived attraction of various PDs to the dominant (Brown, Tan, & Baker, 2021). Further, while Western harmony textbooks consistently organize ordering within the PD according to a regulative syntax (e.g., IV goes to ii), authors differ on its rationale and are rarely explicit about the repertoire(s) on which it is based (e.g., Clendinning & Marvin, 2021; Gauldin, 2004; Kostka, Payne, & Almén, 2018; Laitz, 2008; Piston & deVoto, 1978; Shaffer, Hughes, & Moseley, 2014; Snodgrass, 2015). The PD is also said to be an essential feature of complete cadential closure (Caplin, 1998, 2013; Rohrmeier & Neuwirth, 2015; Sears, Caplin, & McAdams, 2014), but this has yet to be systematically examined in corpora. Finally, the role of PDs at various formal locations is underexplored in both textbooks and in empirical research.
To facilitate study of these claims, we analyzed all 22 sonata-allegro movements from the Mozart piano sonatas and generated a new dataset containing every occurrence of the dominant (V), the three chords preceding each V, and their formal location. 2 We considered but ultimately chose not to pursue two other approaches to studying the PD function: finding all tonics and their preceding harmonies, and tracking all PDs and where they progress. Had we focused on tonics as our starting point, PDs in phrases ending with half-cadences would be missed. In the second case, finding all possible PDs first would have been a challenging task, since the category contains a wide variety of harmonies that have multiple functional possibilities. For instance, the subdominant harmony does not always progress to V, e.g., in I–IV–I or when it functions as a pedal IV6/4. Thus, we adopted a strategy of finding all Vs first, a bottom-up approach and one consistent with Nobile's (2016) stance that anything preceding V may be a PD. 3 As we describe below, the layout of our dataset allows users to view approaches to the dominant at a glance.
Corpus-based approaches to harmonic syntax are well established. Several earlier studies have focused on the Bach chorales, which are also staples in theory pedagogy (e.g., Quinn & Marvromatis, 2011; Rohrmeier & Cross, 2008; Tymoczko, 2003, 2010; White & Quinn, 2018). Other datasets of tonal repertoire provide access to Roman numeral analyses of works by numerous composers (e.g., Cuthbert & Ariza, 2010; Shaffer, Vasiete, Jacquez, Davis, Escalente, Hicks, McCann, Noufi, & Salminen, 2020, after Burgoyne 2011; Temperley, 2009; White & Quinn, 2016). Recent datasets also share expert-labeled Roman numeral analyses (e.g., de Clercq & Temperley, 2011; Devaney, Arthur, Condit-Schultz, & Nisula, 2015; Hentschel, Neuwirth, & Rohrmeier, 2021; López, 2021; Moss, Neuwirth, Harasim, & Rohrmeier, 2019; Tymoczko, 2010).
Only a few existing corpus studies include cadential labels (e.g., de Clercq, 2015; Duane, 2019; Ito, 2014; Martin & Pedneault-Deslauriers, 2015; Raz, Chawin, & Rom, 2021; Sears, 2017; van Kranenburg & Karsdorp, 2015), as noted by Hentschel, Neuwirth, and Rohrmeier (2021) in their newly published data report. Our dataset shares similarities with that of Hentschel, Neuwirth, and Rohrmeier (2021), although we created it independently. Like our dataset, Hentschel, Neuwirth, and Rohrmeier's (2021) dataset tracks harmonic, cadential, and metric information within the Mozart piano sonatas (differences in our approach to cadences are described below). However, while their dataset catalogues chords across all movements, our dataset focuses on approaches to V within sonata-allegro movements and additionally takes formal (thematic) location into account. We present information in a single table that easily allows researchers to study the pre-dominant function at various formal levels and cadential types, illustrating approaches to V within the larger context of sonata form.
Mozart piano sonatas were selected for the study of PDs because they are ubiquitous in North American theory textbooks. We surveyed the seven most popular textbooks and found that examples from these sonatas appear on an average 29 pages per book. In the two textbooks that occupy 54% of the market share (Ewell, 2020), those by Kostka, Payne, and Almén (2018) and by Clendinning and Marvin (2016), Mozart piano sonatas appear on the greatest number of pages, tied only with Bach chorales. This emphasis on Mozart piano sonatas is extended into scholarly literature; for example, in a chapter on understanding cadential syntax (Rohrmeier & Neuwirth, 2015), Mozart piano sonatas are the most frequently discussed examples out of any other repertoire/composer. Yet, despite the frequency with which this repertoire is referenced, its harmonic-syntactical properties, particularly in relation to formal context, are underexplored in corpus studies. This dataset will allow researchers to test hypotheses regarding pre-dominant usage at different cadences and regions within sonata form. We contend that this can contribute to a refinement of claims made in pedagogical contexts. A similar approach can be taken to studying tonal music by other composers; we intuit that differences in PD distributions will be found from composer to composer and across genres.
METHOD
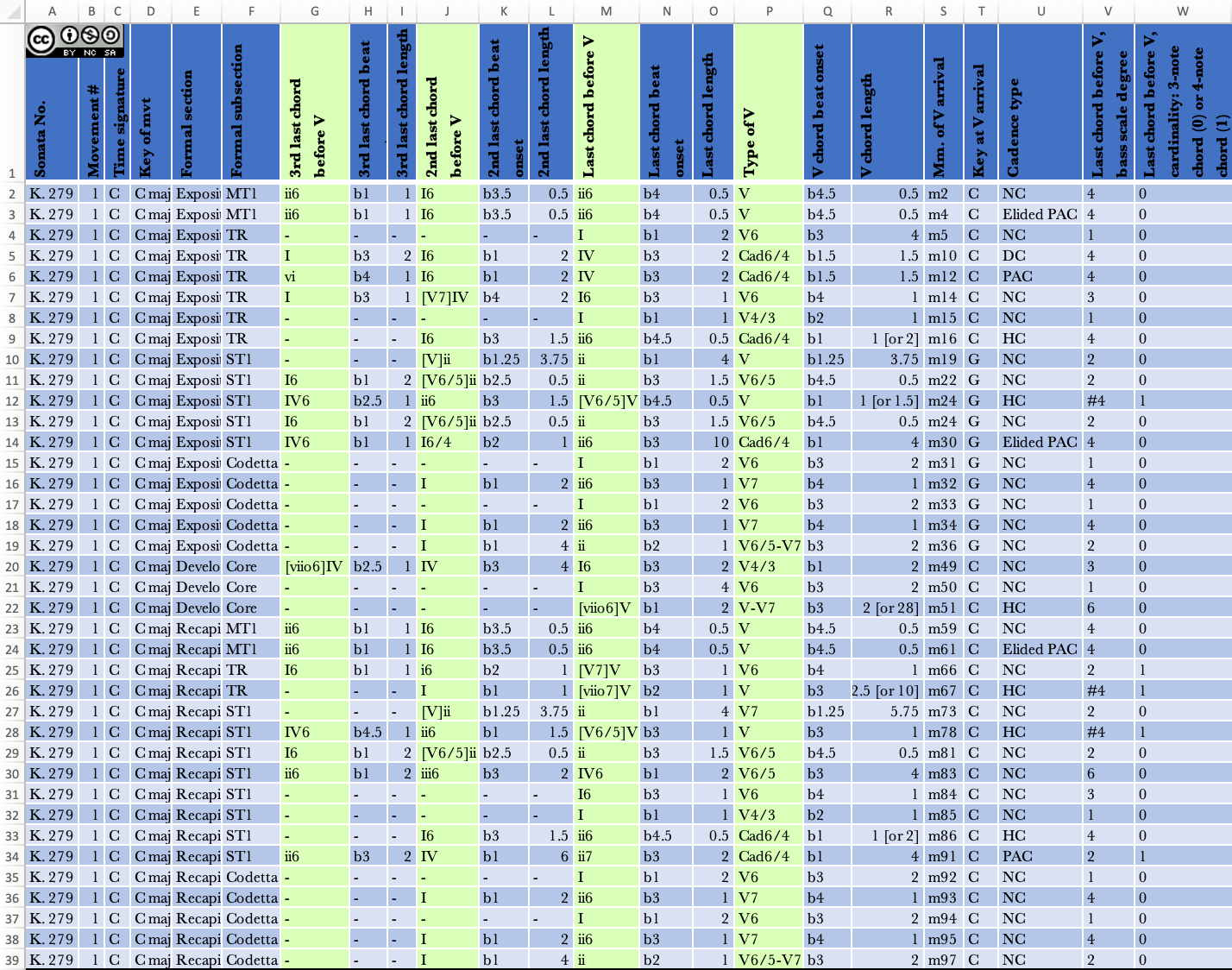
The following dataset can be found here: https://osf.io/7pa6m/?view_only=36d6fd8c9fda4a1398e68445b509959e. Figure 1 illustrates a portion of the dataset; this excerpt includes all rows (and thus all V chords) for K. 279, first movement.
Dataset
The dataset contains expert analyses of harmonic approaches to the dominant in all 22 sonata-allegro movements for piano by W. A. Mozart, all but two of which are in a major key. Analyses were based on scores held in the digitized Neue Mozart-Ausgabe (https://dme.mozarteum.at/DME/nma/start.php?l=2), an Urtext edition. The dataset identifies 1,129 instances of V in this repertoire, along with up to three harmonies preceding V. Each string of harmonic events is accompanied by contextual information: sonata, movement, time signature, global key, local key, location within sonata form, measure in which V arrives, beat onset, chord length, and type of cadence to which the V belongs (if applicable). The bass note of the chord immediately preceding V and its cardinality (three or four notes) is also included.
Format of Dataset
The dataset is presented as an Excel table, which allows users to filter or sort data easily by column headers. Each row is structured around a single instance of V; Column P, in light green, displays the type of dominant harmony, and columns M, J, and G, also in light green, display up to three harmonies preceding this dominant, using Roman numerals. The order of these harmonies from left to right (i.e., G, J, M, P) follows their temporal appearance in the work. A dash ("-") appears when the harmony preceding V belongs to a previous phrase or is itself a dominant harmony, which would then be found in the previous row; in other words, dashes indicate that fewer than three chords separate two instances of dominant harmony. We note that in practice, V may be preceded by more than three non-V harmonies, but our dataset only captures three, because we anticipated that there would be too few instances of four harmonies before V to be analytically useful. 4 Still, future research could explore this possibility.
Directly to the right of each harmony column are columns for beat onset and chord length (columns Q–R, N–O, K–L, and H–I, respectively). Column S provides the measure number for the arrival of the dominant. Columns A–E provide large-scale identifiers that are given by cues in the score: Köchel and movement number, time signature of the movement, key of the movement, and large-scale formal functions (exposition, development, recapitulation). Columns F, T, and U show, respectively, the formal subsection, local key associated with V, and cadence type; information in these columns was determined by informed interpretation. The last two columns, V and W, show the bass scale degree and cardinality of the last chord before V. Further details about each of these columns is provided below.
Dataset Creation Process
Jenine Brown (JB) and Daphne Tan (DT) created the columns for data entry. Michelle Lin (ML) identified and created rows for all V harmonies within first-movement and third-movement sonata forms, filling in the columns. JB and DT separately reviewed the entire dataset twice: in the first pass, Roman numerals, chord onsets, and chord lengths were confirmed; in the second pass, formal locations and cadence types were confirmed. Discrepancies in interpretation were discussed at an initial stage between JB, DT, and ML, and at a later stage between JB and DT, to arrive at consensus. Some discrepancies led us to refine our analytical methodologies and revisit previous analyses to ensure that the methodologies were applied consistently across the entire dataset. No computational tools (e.g., key finding algorithms, tools for phrase segmentation) were used.
Description of Columns and Annotation Standard
COLUMNS A–F
Column A presents the Köchel number (catalogue number abbreviated as "K.") of the sonata for each V. Column B lists the sonata-form movement; there are 17 first movements and 5 third movements in the dataset. Column C states the time signature for the movement (none of the movements have internal meter changes). Column D lists the starting and ending key of the movement, which in all cases matches the key signature for the movement.
Columns E and F describe the formal location of each V. Column E provides the large-scale formal function of exposition, development, or recapitulation. Column F states themes, theme-like units (such as the transition, TR), and post-cadential units that operate at a lower level of the formal hierarchy (such as codettas). The main theoretical basis for these categories is Caplin (1998, 2013), which recognizes the possibility of multiple main themes (MT) and subordinate themes (ST). Within the development section, we borrow the terms "core" and "pre-core" from Caplin, but employ them in a more general way. That is, we define the "core" as a passage that is harmonically unstable, features sequential repetition and greater rhythmic activity, and usually has V as the harmonic goal (half-cadence or dominant arrival); this can be preceded by a "pre-core" that is "generally more relaxed" and may involve complete or incomplete thematic units (Caplin, 1998, p. 147). We note that Caplin suggests other organizational possibilities for the development section, including "pseudo-core," "transition-like unit," and "subordinate themelike unit" (1998, pp. 155–157). For simplicity, these options were coded as "core" in the dataset; future research could explore approaches to V within these more nuanced categories.
COLUMNS G–T
Column P lists the type of dominant harmony that is the focus of the row. A variety of options can appear in this column, including the V triad and its inversions, V7 and its inversions, and the cadential 6/4 (containing the notes of the tonic chord in second inversion), which marks the beginning of dominant function. There are also moments in which one V type begins but moves to a different inversion via bass arpeggiation. For instance, "V–V4/2" indicates a V triad moving to a third-inversion V7 chord.
Column S displays the measure in which the dominant harmony appears, and column T indicates the local key of V and the three harmonies leading up to it. A local minor key within a global major key could suggest the presence of modal mixture. For instance, in K. 533/1, a V triad appears on the downbeat of m. 41, at the end of the transition. The three harmonies leading up to this, and indeed all harmonies from mm. 36–41, are in the minor mode, while the music preceding this passage and the beginning of the subordinate theme are in C major. 5
Working backward from the dominant harmony, columns M, J, and G list the three harmonies prior to the dominant. As mentioned above, dashes appear if a harmony belongs to a previous phrase or is another V chord. An example from K. 279/1, shown in Figure 2, illustrates the second case. Measure 30 contains a cadential 6/4 and its resolution, leading to an elided perfect authentic cadence, events which are captured in the dataset in row 14 (see Figure 1). In m. 31, another dominant harmony occurs after the cadence; this V6 is included in row 15 of the dataset, as is the root-position tonic chord that precedes it. The second-last chord before the V6, however, is the cadential 6/4 and its resolution, which is already accounted for in row 14. Thus, there are no harmonies entered in columns J and G in row 15.
A variety of harmonies can occur in the last chord, second-last chord, and third-last chord before V (columns M, J, G). Uppercase and lowercase Roman numerals differentiate between major and minor harmonies; diminished (°) and half-diminished (ø) symbols, inversions, and chordal sevenths are also used where applicable. Secondary dominants appear in square brackets: [V6/5]V means "V6/5 of V"; we preferred this nomenclature to the potentially ambiguous alternative "V6/5/V," noting that one could search all instances of secondary dominants with the term "]V". The Neapolitan chord is coded as ♭II or ♭II6 in this dataset and augmented sixth chords appear as It+6, Fr+6, and Ger+6; searching "+6" will call up all instances of augmented sixth chords. Note that occurrences of the mediant with a chromatically raised third (III, ^3-♯^5-^7) leading to vi are interpreted as [V]vi and the submediant with a chromatically raised third (VI, ^6-♯^1-^3) leading to ii as [V]ii. Beyond these cases, occurrences of III and VI as chromatic substitutes in a major key are very uncommon: VI never occurs without a subsequent ii, and III alone appears only once: in the development of K. 332/1, moving directly to iii (row 436).
In contrast, harmonies built on the flattened mediant (♭III, ♭^3-^5-♭^7) and flattened submediant (♭VI, ♭^6-^1-♭^3) appear somewhat more frequently. For clarity, we use a flat symbol ("♭") before the Roman numeral in all cases, even though a major-key movement may have temporarily slipped into the parallel minor. In the two minor-mode movements (K. 310/1 and K. 457/1), we also use "♭III" and "♭VI" to refer to diatonic harmonies built on the mediant and submediant, a decision motivated by ease of searching; for instance, a researcher might want to know how many times the chord containing ♭^6-1-♭^3 precedes the dominant. Note that ♭III is very infrequent, occurring three times in K. 310/1 and twice in K. 332/1, all within Column G (third-last chord before V).
Occasionally, the texture of the music can pose a challenge to clear harmonic interpretation, particularly when melody alone is present or when the two hands are heard in unison. In cases where the three authors were reasonably certain of the harmony outlined, entries take the form "unisons/melody implying the X chord." When the harmonic framework is more ambiguous, we opt for statements like "unisons on ^Y" and "unisons moving through ^Y and ^Z," where ^Y and ^Z are scale degrees that are emphasized. We note that melody alone or unison texture is relatively infrequent; for instance, immediately before V (column M), these textures account for only 26 of 1129 entries (2.3%). Other issues of harmonic ambiguity, for instance, whether a chord is ii6/5 or ii6 with a passing ^1, were discussed on a case-by-case basis by the authors.
Columns H, K, N, and Q show the beat onset for the four possible harmonic events (dominant and three preceding chords). The terminology used is as follows: "b1" indicates that the chord occurs on beat 1. An indication of "b2.5" means that the chord begins on beat two-and-a-half, and "b3.75" means that the chord begins on beat three-and-three-quarters (e.g., the last sixteenth note in a group of four). Seventeen of the 22 sonata-form movements are in meters with a quarter-note beat. The same annotation standard applies to three simple-meter movements where the beat is not a quarter note: K. 533/1 is in cut time (beat is the half note), and K. 280/3 and K. 283/3 are in 3/8 (beat is the eighth note). For the two movements in compound time, 6/8 (K. 576/1 and K. 332/3), the beat is the dotted quarter; here, beat onset annotations include thirds, e.g., "b2.67" means the chord starts on the fifth eighth note in the measure.
Columns I, L, O, and R describe the length of the four possible harmonic events, using whole numbers and fractions, e.g., "1" corresponds to one beat, "2.5" means two and a half beats in simple meter, and "0.33" means one eighth note in 6/8 meter. Column R occasionally gives two duration choices for researchers to consider, with a longer duration in square brackets. For example, in Figure 1, row 9, K. 279/1, the dominant in m. 16 sounds for one beat, but one may hear the dominant ringing for two beats, across the rest that follows the chord. Similarly, in m. 51 (row 22), a root position V triad lasting two beats articulates a half-cadence at the end of the development, but dominant harmony is prolonged for 28 beats due to the repeated Gs in mm. 52–56 and the right-hand figuration in mm. 56–57. Note, too, that the V triad in m. 51 later becomes V7; this is captured in column P. Such dominant prolongations are common at the ends of transitions and developments, usually corresponding to post-arrival "standing on the dominant" (Caplin, 1998). Researchers might wish to consider whether there is any association between types of pre-dominant harmonies and dominant length.
COLUMN U
Column U includes the type of cadence in which the dominant participates. Caplin (1998, 2013) again provides the main theoretical basis for our analytical decisions. The three standard possibilities for cadences are perfect authentic cadences (PAC), imperfect authentic cadences (IAC), and half cadences (HC). 6 In some instances, the arrival of a PAC simultaneously marks the beginning of a new formal unit; these are labeled "elided PAC" in the dataset. We also identify instances of abandoned cadences (AC), deceptive cadences (DC), and evaded cadences (EC). Further, following Caplin, we identify a few "dominant arrivals" (D arrival), where dominant harmony signals the end of a formal unit but is heard as noncadential, because it is inverted, contains a chordal seventh, is not preceded by a harmonic progression, or there is a noncongruence between the harmonic arrival and the melodic-motivic arrival. Finally, when a dominant harmony does not participate in any of these scenarios, an entry of "no cadence" (NC) appears. 7
COLUMNS V AND W
Column V indicates the bass scale degree in the chord before V, and Column W lists whether the chord heard directly before the dominant is a three-note chord (coded in the dataset as "0") or whether it is a four-note chord (coded as "1"). When there is no chord immediately prior to V or if there is only melodic motion, an entry of "n/a" appears (77 instances in the dataset).
DATA USAGE AND APPLICATIONS
This dataset can be used to examine the interaction of harmony and form in Mozart's sonata-allegro movements for piano. Our primary motivation was to allow researchers to focus on the pre-dominant function: a standard concept in North American music theory teaching, yet one that is undertheorized (Brown, Tan, & Baker, 2021). There are many possible avenues of investigation, such as: comparing harmonies before V within different cadential contexts and within different formal locations; cataloguing recurring and paradigmatic successions of harmonies before V (i.e., PD complexes); examining possible relationships between PD type and metric placement, chord duration, and global meter; tracing the evolution of Mozart's PD usage in these sonatas over the period in which they were composed (~1774–1789); and comparing PD usage in this dataset to other corpora, by Mozart and by other composers. Initial findings can be found in Tan, Brown, and Lin (2021) and in Brown, Tan, and Boerner (under review). These research issues have pedagogical implications. For instance, students stand to gain more nuanced expectations for how specific PD harmonies function as cadential preparation and within sonata form. Additionally, a comparative study of Mozart's PD usage to that of other composers would offer a corrective to prescriptive, rule-based approaches that generalize across several different repertoires. Indeed, an initial comparison of PD usage in Bach and Beethoven suggests some important differences between the composers (Brown, Tan, Moranis, & Orlando, 2021), and these corpora could be compared to this Mozart dataset. Broadly, we encourage researchers to use this dataset for empirically driven, context-sensitive approaches to harmonic syntax.
END MATTER
Author note
Michelle Lin is now at the University of Texas at Austin.
Author contributions
ML created an initial draft of the dataset. JB and DT reviewed and finalized the dataset. JB and DT contributed equally to writing the manuscript.
Funding
This research was supported in part by a University of Toronto Excellence Award for ML, supervised by DT.
NOTES
- Correspondence can be addressed to: Jenine Brown, The Peabody Conservatory of The Johns Hopkins University, 1 E. Mt. Vernon Pl., Baltimore, MD, 21202, Jenine.Brown@jhu.edu.
Return to Text - Throughout this data report and unless otherwise specified, "V" refers to the general category of dominant harmony that includes the root-position triad built on ^5 and its inversions, the seventh chord built on ^5 and its inversions, and the cadential 6/4 (with ^5 in the bass and ^1 and ^3 in upper voices). We use this Roman numeral rather than the functional label "D" to highlight the inclusion of ^5 and to avoid confusion with column D in the dataset and the key of D major.
Return to Text -
Indeed, Temperley (2009) has shown that the tonic chord is the most frequent chord before V in the Kostka-Payne corpus, and our dataset shows that this is also the case in this Mozart corpus.
Return to Text -
The column containing the chord directly before V has 51 blanks (Column M, 5%), whereas the chord before that contains 521 blanks (Column J, 46%), and the chord before that has 727 blanks (Column G, 64%).
Return to Text -
We also note that this dataset attempts to capture chord-to-chord successions, but other interpretations, which take a more reductive or less reductive approach, may be possible. Future versions of this dataset could include multiple levels of harmonic progression.
Return to Text -
Martin and Pedneault-Deslauriers (2015) present a corpus study of Mozart's HC. Of the 70 instances of HCs in the sonata-form movements that they list, our dataset agrees with 69. The sole difference lies in K. 570/1, m. 22, where we analyzed the V as No Cadence (NC) rather than HC.
Return to Text -
As Caplin (1998) notes, codettas may contain alternations of tonic and dominant harmonies and even harmonic progressions with predominant, dominant, and tonic, thus resembling cadential units (p. 16). Like Caplin, we reserve the term "cadence," for the structural end of a theme, and recognize codettas as post-cadential functions that themselves do not contain cadences. This decision may contribute to interpretive differences between our dataset and other datasets featuring cadences in Mozart. Indeed, we compared our dataset to the Annotated Mozart Sonatas corpus (Hentschel, Neuwirth, & Rohrmeier, 2021) for cadences listed in K. 279/1 and found only 60% agreement; the Annotated Mozart Sonatas identifies 20 cadences in this movement, while we identify only 12. For instance, the Annotated Mozart Sonatas identifies PACs in mm. 3, 33, 35, and 37, but we call these NCs (see rows 2, 16, 18, and 19), as we contend that these either occur too soon within the main theme or follow the formal end of the subordinate theme and belong to post-cadential codettas.
Return to Text
REFERENCES
- Brown, J. L., Tan, D., & Boerner, V. (Under review). “A context-sensitive analysis of harmonic approaches to the dominant.”
- Brown, J. L., Tan, D., & Baker, D. J. (2021). The perceptual attraction of pre-dominant chords. Music Perception, 39(1), 2140. https://doi.org/10.1525/mp.2021.39.1.21
- Brown, J. L., Tan, D., Moranis, R., & Orlando, S. (2021, July). The pre-dominant function at cadences in Bach and Beethoven. Poster presented at the 16th International Conference on Music Perception and Cognition, Online.
- Burgoyne, J. A. (2011). Stochastic processes & database-driven musicology. Doctoral dissertation, McGill University, Canada. Retrieved from: https://escholarship.mcgill.ca/concern/theses/d217qt98k
- Caplin, W. E. (1998). Classical form: A theory of formal functions for the instrumental music of Haydn, Mozart, and Beethoven. Oxford, England: Oxford University Press.
- Caplin, W. E. (2013). Analyzing classical form: An approach for the classroom. New York, NY: Oxford University Press.
- Clendinning, J. P., & Marvin, E. W. (2016). The musician's guide to theory and analysis (3rd ed.). New York, NY: W. W. Norton.
- Clendinning, J. P., & Marvin, E. W. (2021). The musician's guide to theory and analysis (4th ed.). New York, NY: W. W. Norton.
- Cuthbert, M. S., & Ariza, C. (2010). music21: A toolkit for computer-aided musicology and symbolic music data. In J. S. Downie & R. C. Veltkamp (Eds.), Proceedings of the 11th Conference of the International Society for Music Information Retrieval (ISMIR) (pp. 637–642). Canada: ISMIR. https://doi.org/10.5281/zenodo.1416114
- de Clercq, T. (2015). A model for scale-degree reinterpretation: Melodic structure, modulation, and cadence choice in the chorale harmonizations of J. S. Bach. Empirical Musicology Review, 10(3), 188–206. https://doi.org/10.18061/emr.v10i3.4334
- de Clercq, T., & Temperley, D. (2011). A corpus analysis of rock harmony. Popular music, 30(1), 47–70. https://doi.org/10.1017/S026114301000067X
- Devaney, J., Arthur, C., Condit-Schultz, N., & Nisula, K. (2015). Theme And Variation Encodings with Roman Numerals (TAVERN): A new data set for symbolic music analysis. In M. Müller & F. Wiering (Eds.), Proceedings of the 16th Conference of the International Society for Music Information Retrieval (ISMIR) (pp. 728–34). Canada: ISMIR. https://doi.org/10.5281/zenodo.1417497
- Duane, B. (2019). Melodic patterns and tonal cadences: Bayesian learning of cadential categories from contrapuntal information. Journal of New Music Research, 48(3), 197–216. https://doi.org/10.1080/09298215.2019.1607396
- Ewell, P. (2020). Music theory and the white racial frame. Music Theory Online, 26(2). https://doi.org/10.30535/mto.26.2.4
- Gauldin, R. (2004). Harmonic practice in tonal music (2nd ed.). New York, NY: W. W. Norton.
- Guck, M. A. (1978). The functional relations of chords: A theory of musical intuitions. In Theory Only, 4(6), 29–42.
- Hentschel, J., Neuwirth, M., & Rohrmeier, M., (2021). The Annotated Mozart Sonatas: Score, harmony, and cadence. Transactions of the International Society for Music Information Retrieval, 4(1), pp. 67–80. https://doi.org/10.5334/tismir.63
- Ito, J. P. (2014). Koch's metrical theory and Mozart's music: A corpus study. Music Perception: An Interdisciplinary Journal, 31(3), 205–222. https://doi.org/10.1525/mp.2014.31.3.205
- Kostka, S. M., Payne, D., & Almén, B. (2018). Tonal harmony, with an introduction to twentieth-century music (8th ed.). New York, NY: McGraw-Hill.
- Laitz, S. G. (2008). The complete musician: An integrated approach to tonal theory, analysis, and listening (2nd ed.). New York, NY: Oxford University Press.
- López, N. N. (2021). The Joseph Haydn harmonic analysis annotations dataset. Retrieved from: https://github.com/napulen/haydn_op20_harm
- Martin, N. J., & Pednealut-Deslauriers, J. (2015). The Mozartean half cadence. In M. Neuwirth & P. Bergé (Eds.), What is a Cadence? Theoretical and Analytical Perspectives on Cadences in the Classical Repertoire (pp. 185–213). Leuven, Belgium: Leuven University Press.https://doi.org/10.2307/j.ctt14jxt45.9
- Moss, F. C., Neuwirth, M., Harasim, D., & Rohrmeier, M. (2019). Statistical characteristics of tonal harmony: A corpus study of Beethoven's string quartets. PLoS ONE 14(6), e0217242. https://doi.org/10.1371/journal.pone.0217242
- Nobile, D. (2016). Harmonic function in rock music: A syntactical approach. Journal of Music Theory, 60(2), 149–180. https://doi.org/10.1215/00222909-3651838
- Piston, W., & deVoto, M. (1978). Harmony (4th ed.). New York, NY: W. W. Norton.
- Quinn, I., & Mavromatis, P. (2011). Voice-leading prototypes and harmonic function in two chorale corpora. In C. Agon, E. Amiot, M. Andreatta, G. Assayag, J. Bresson & J. Manderau (Eds.), Mathematics and computation in music: proceedings of the Third International Conference (pp. 230-240). Berlin, Germany: Springer-Verlag. https://doi.org/10.1007/978-3-642-21590-2_18
- Raz, O., Chawin, D., & Rom, U. B. (2021). The Mozart expositional punctuation corpus: A dataset of interthematic cadences in Mozart's sonata-allegro exposition. Empirical Musicology Review, 16(1). https://doi.org/10.18061/emr.v16i1.7648
- Rohrmeier, M., & Cross, I. (2008). Statistical properties of tonal harmony in Bach's chorales. In K. Miyazaki, M. Adachi, Y. Hiraga, Y. Nakajima & M. Tsuzuki (Eds.), Proceedings of the 10th International Conference on Music Perception and Cognition, (pp. 619–627). Sapporo, Japan.
- Rohrmeiher, M., & Neuwirth, M. (2015). Towards a syntax of the Classical cadence. In M. Neuwirth & P. Bergé (Eds.), What is a Cadence? Theoretical and Analytical Perspectives on Cadences in the Classical Repertoire (pp. 285–336). Leuven, Belgium: Leuven University Press. https://doi.org/10.2307/j.ctt14jxt45
- Sears, D. R. W. (2017). The classical cadence as a closing schema: Learning, memory, and perception. Doctoral dissertation, McGill University, Canada.
- Sears, D. R. W., Caplin, W. E., & McAdams, S. (2014). Perceiving the classical cadence. Music Perception, 31, 397–417. https://doi.org/10.1525/mp.2014.31.5.397
- Shaffer, K., Hughes, B., & Moseley, B. (2014). Open music theory (Shaffer, K., & Wharton, R., Eds.). Hybrid Pedagogy Publishing. Retrieved from: http://openmusictheory.com/
- Shaffer, K., Vasiete, E., Jacquez, B., Davis, A., Escalante, D. Hicks, C., McCann, J., Noufi, C., & Salminen, P. (2019). A cluster analysis of harmony in the McGill Billboard dataset. Empirical Musicology Review, 14(3–4), 146–162. https://doi.org/10.18061/emr.v14i3-4.5576
- Snodgrass, J. S. (2015). Contemporary musicianship: Analysis and the artist (1st ed.). New York, NY: Oxford University Press.
- Stein, D. (1983). The expansion of the subdominant in the late nineteenth century. Journal of Music Theory, 27(2), 153–180. https://doi.org/10.2307/843513
- Tan, D., Brown, J. L., & Lin, M. L. (2021, July). A context-sensitive analysis of pre-dominant chords in Mozart. Paper presented at the 16th International Conference for Music Perception and Cognition, Online.
- Temperley, D. (2009). A statistical analysis of tonal harmony. Retrieved from: http://davidtemperley.com/kp-stats/
- Tymoczko, D. (2003). Function theories: A statistical approach. Musurgia, 10(3–4), 35–64.
- Tymoczko, D. (2010). Local harmonic grammar in Western classical music. https://dmitri.mycpanel.princeton.edu/mozart.pdf
- van Kranenburg, P., & Karsdorp, F. (2014). Cadence detection in Western traditional stanzaic songs using melodic and textual features. In H-M. Wang, Y-H. Yang & J. H. Lee (Eds.), Proceedings of the 15th Conference of the International Society for Music Information Retrieval (ISMIR), (pp. 391–396). https://doi.org/10.5281/zenodo.1416172
- White, C. W., & Quinn, I. (2016). The Yale-Classical Archives Corpus. Empirical Musicology Review, 11(1), 50–58. https://doi.org/10.18061/emr.v11i1.4958
- White, C. W., & Quinn, I. (2018). Chord context and harmonic function in tonal music. Music Theory Spectrum, 40(2), 314–37. https://doi.org/10.1093/mts/mty021