INTRODUCTION
A listener may experience music as "difficult," "complex," or even "incomprehensible." Many listeners will put such music aside, and look for alternatives, unless they are explicitly interested in the reasons why a particular musical piece is perceived as it is. This paper explores this specific interest in the context of children's folk songs. It specifically examines—and refutes—the assumption of many musicologists that children's folk songs are simple or trivial.
Behind each piece of music is the story of the creation of a musical structure, covering different musical elements and dimensions, and a musical syntax, a more or less formal characterization of rules that define the permissible structure—that is, how the constituent parts in a piece may be formed and combined over time (Rohrmeier & Pearce, 2018).
Thus, Western tonal music is often considered to be fundamentally syntactic. A syntactic feature is, e.g., the hierarchical structure that is achieved by combining perceptually discrete related elements, on a range of timescales. Another syntactic feature is the sequential relation between musical elements, because the "syntactic functional psychological qualities" of some musical elements depends on the relation with others (Bigand et al., 2014, p. 2).
Several studies (e.g., Bigand & Poulin-Charronat, 2006; Koelsch & Jentschke, 2008; Bigand et al., 2014; Mihelač et al., 2018; Mihelač & Povh, 2020a) point to the significance of musical syntax, and its contribution to the notion of structure which is regular—i.e., which conforms to syntactic rules—as opposed to irregular—non-conformant—structure. Broadly, these studies take either a traditional empirical approach (viz., involvement of listeners in experiments and in the evaluation of music), or, recently, a computational approach. The studies explore how musical syntax, and deviation in a musical structure, which occurs when structure does not conform with syntax, are related to the listener's perception of (ir)regularity in musical structure, and their acceptance, pleasure, and understanding of musical pieces and/or musical genres.
Taking the more traditional approach can be costly, and also scientifically challenging, because it is difficult to avoid subjectivity in evaluation tasks, both in musical experts and in listeners without musical training. Furthermore, it is difficult to replicate the results, as the response in a task can vary significantly between hearings, even if the same participants are involved in the replication (Mihelač & Povh, 2020b).
In recent decades, computational approaches to the study of music have offered a more objective analysis of music (Potter, Wiggins, & Pearce, 2007), enabling identification of significant features (such as semiotic structure: Wiggins, 2010) in a musical structure, and comparison with the processing and production of music in humans. These computational methods are now becoming capable of simulating the human perception of music to some degree, especially where they are based on an underlying cognitive theory.
The fact that computational models can be efficiently used in the simulation of the human perception of music was the motivation for a recent study by Mihelač and Povh (2020a). Human experts involved in the detection of (ir)regularity in the musical structure in a previous study (Mihelač & Povh, 2020b), and the evaluation of (ir)regularity of musical excerpts by listeners were replaced by simulating their responses with a computational model, Information Dynamics of Music (IDyOM: Pearce, 2005).
The artificial model of the perception of (ir)regularity obtained by Mihelač and Povh (2020a) is shown to accord with human perception of irregularity in the previous study (Mihelač & Povh, 2020b), suggesting that expert-based detection of (ir)regularity in musical structure can usefully be replaced by a suitable computational model. In the current study, we used a similar approach to the (ir)regularity in musical structure, by simulating and detecting the (ir)regularity in musical examples with the computational model IDyOM, and our own algorithm, Ir_Reg, which classifies melodies according to regularity of the musical structure. The data for this study consisted of monophonic children's folk songs. We used this corpus to show that children's folk songs, often presumed to be simple and regular in structure (Herzog, 1944; Romet, 1980; Pond, 1981; Nettl, 1983; Ling, 1997), can be also complex.
Main contributions
The main contributions of this paper are:
- We explain musical structure in children's folk songs from the perspective of (ir)regularity, by observing pitch, interval, implied harmonies, duration, and contour.
- We develop a novel algorithm, Ir_Reg, to find possible "candidates" with irregular structure in a dataset of which no prior musical analysis is available.
- We show that artificial modelling of human perception of (ir)regularity in children's folk songs can add considerable useful contribution to the understanding of this genre.
BACKGROUND AND RELATED WORK
Music is an art of "humanly organized sounds" (Godt, 2005, p. 84). Thus, sounds are not merely randomly distributed, but are organized in a specific order: discrete units (sounds) into smaller parts, smaller parts into larger parts, up to the level of a musical piece, creating a hierarchical structure, which is one of the cornerstones of music theory and music cognition (Levitin & Menon, 2000). A set of permissible and rigid rules, defined as musical syntax, defines how this structure has to be organized, covering a wide range of different fundamental musical elements (Berezovsky, 2019).
According to studies (e.g., Cohen, 2003; Marcus, 2003; Cohen & Katz, 2013), musical syntax differs not only between different cultures (in non-Western and Western tonal music traditions), but also in different styles within Western tonal music (e.g., the Middle Ages, the Renaissance, the period of tonal music, from ca. 1600–1918, and the Modern period after 1918), due to the evolution of musical-syntactic rules over time (Meyer, 1989; Klein & Jacobsen, 2014; Vuvan & Hughes, 2019). Changes within these periods are considered as compositional choices (Meyer, 1989), rather than as changes in musical language.
Several empirical studies suggest that musical syntax is represented cognitively (e.g., Bharucha & Stoeckig, 1986; Tillmann, Bharucha, & Bigand, 2000) and that observable neural correlates exist (e.g., Janata et al., 2002; Koelsch & Siebel, 2005). Manipulating any of the fundamental musical elements in a structure impacts the reported feeling of regularity (Rohrmeier, 2011; Pole, 2014; Rohrmeier & Pearce, 2018; Mihelač & Povh, 2020a,b) and its identification (Bruner, Wallach, & Galanter, 1959). Patel (2003) argues that, following manipulation of the order of elements (parts), a piece of music loses its identity, which accords with the processing of sequential information and structure in non-musical domains (Garner, 1974).
A piece of music is considered to be regular (from the perspective of musical syntax and/or the perception of listeners), when a strong structure exists, with periodic dominant musical elements (patterns), and there are strong relationships between these patterns (Wu et al., 2000). Conversely, an irregular piece contains a non-structured or weakly structured texture, with a small number of detectable patterns with weak interrelationships (Kramer, 1988). Klein and Jacobsen (2014) point out that for every compositional rule in a given tonal style a complementary regularity is generated for a complementary tonal style: a given structure, perceived as syntactically regular in context of one piece, can appear to be irregular in another (e.g., frequent endings on dominant triad in folk songs from Serbia, perceived as a syntactically "regular", however as "irregular" in children's folk songs from the same country, as these songs ends on the tonic triad).
Findings from various studies outline that a stronger feeling of regularity is perceived when similar parts are periodically repeated, either in an "absolute repetition condition", where parts are repeated identically, or in a "relative repetition", where parts are considered to be conditionally identical (Bader, Schröger, & Grimm, 2017). 1 Relative repetition is important in the development of motifs that form the structure of longer pieces (Deliège, 1987; Cambouropoulos, Crawford, & Iliopoulos, 2001). Thus, the prevalence of repetition in music, found in all known human cultures, is unsurprising, as is the fact that listeners tend to listen repeatedly to familiar musical pieces (Margulis, 2014). Repetition is a fundamental characteristic of music, a "design feature" of music (Fitch, 2006), contributing significantly to our understanding of music (Schoenberg, Strang, & Stein, 1967).
Bruner, Wallach, and Galanter (1959) point out that perception of recurrent regularities (parts/patterns repeated at pitch or transposed repeated patterns) is impacted either by elements that mask the identification of recurrent regularities (e.g., an input-stimulus, which does not conform the recurrent series in a sequence) or by the regularity itself, in the case where it "exceeds the memory span" of an observer (Bruner, Wallach, & Galanter, 1959, p. 84). The identification of recurrent regularity in a musical structure requires that a listener either construct a model to represent this regularity or deploy a model, which they have previously constructed. In either case, the success of identification depends on separating recurrent regularities from interfering structures. The greater the number of elements interfering the recurrent regularities, the more noise is found in the stimulus, and consequently the more difficult is the identification of recurrent regularity (Bruner, Wallach, & Galanter, 1959). The perception and identification of recurrent regularities and structural particularities in a musical structure depend on how well the musical structure and its syntax are internalized in listener. The internalization of music, which can be implicit, during mere exposure to music without listening, or explicit, when interacting with music (Pearce & Wiggins, 2012), depends on several factors, such as the listener's musical experience and/or training (Lappe, Steinsträter, & Pantev, 2013; Bangert & Altenmüller, 2003). Lu and Vicario (2014) show that human infants and adults identify recurrent sound patterns even when exposure to musical sequences is passive.
No matter how internalization occurs, internal models of the (permissible) musical structures are generated and applied whenever listening to novel music (Deliège, 1987; Agres, 2019). If the internal models somehow confront the (prescribed) rules of the arrangement of the constituent parts of a musical structure, the structure is perceived not only as irregular, but also as more complex and less enjoyable (Sauvé & Pearce 2019; Mihelač & Povh, 2020b). This is because more effort has to be put into the listening process, as the learned musical syntax and its rules have to be adjusted in order to understand the novel structures (Kramer, 1988).
Musical genres vary from the perspective of the recurrent regularities in musical structure, and from the perspective of musical elements that are emphasized in a repeated at pitch or transposed repeated condition, and therefore contributing more or less to the regularity. In some musical genres (e.g., modernist, and expressly avant-garde approaches), repetition is avoided (Margulis, 2014), and any feeling of surface regularity is deliberately lacking. In some other genres, e.g., in minimalist music, regular structure is achieved by (e.g.) emphasizing the rhythm, using repetitive rhythmic patterns (Johnson, 1994). Another example of music with recurrence regularities in its structure, employing both repeated at pitch or transposed repeated conditions, is children's (folk) songs (Jožef-Beg & Mihelač, 2019), to which we return in Section Information Dynamics of Music: IDyOM.
Several approaches have been used to measure (ir)regularity in musical structure, including subjective evaluation by listeners (e.g., Deutsch, 1980; Tillmann & Bigand, 1996; Mihelač et al., 2018; Mihelač and Povh, 2020b), measurement of neural response (mismatch negativity, MMN) and functional magnetic resonance imaging (fMRI) (e.g., Ulanovsky, Las, & Nelken, 2003; Grahn & Rowe, 2012; Yu, Liu, & Gao, 2015), or simulation of human perception of (ir)regularity using a computational system (e.g., Hansen & Pearce, 2014; Mihelač & Povh, 2020a). The current study uses a computational model to enable a novel approach to the examination of (ir)regularity in the musical structure of children's folk songs.
CHILDREN'S FOLK SONGS
Music "happens to" children all the time, often in singing songs during unrelated activities, and as part of education. However, this seems not to have been understood by adults in earlier decades (Campbell, 1998). As a result, many children's folk songs (defined also as traditional songs), contributions by and for children, may not have been collected. Such collection could contribute to a better understanding of these songs within and between cultures, and of their relation to adult music, within culture. A renewed interest of ethnomusicologists, sociologists, educators, and folklorists in children's folk songs can be seen from 1940 onward, centering on studies of musical content, on the social and cultural significance of children's folk songs and their relationships to the music of adults, on how these songs contribute to the preservation of a particular culture, on how the children's folk songs are transmitted from one generation to another, and so on (e.g., Herzog, 1944; Brailoiu, 1954; Newell, 1963; Blacking, 1973; Nettl & Béhague, 1980; Pond, 1981; Nettl, 1983).
Collections of children's folk songs, from all over the world, include songs created by adults for children, folk songs, as well as songs created by children and passed along to each other. It is sometimes extremely difficult to trace the origin of children's folk songs, as children's songs created by children are often changed and adapted by children in different generations, or even published by adults, due to lack of musical skill in children (e.g., how to transcribe the songs). A similar problem occurs with folk songs (to be found among children's songs), as it is not clear whether these songs have been created by children, or by adults for children. The single exception is lullabies, existing in nearly every culture, which are created by adults for children (Jožef-Beg & Mihelač, 2019). No matter who created them, children's folk songs exhibit many features which also exist also in (other) folk songs, and which are passed from generation to generation (as folk songs), via oral tradition.
Children's folk songs, for which there is still no clear definition (Sutton-Smith, 1999), are tonally and structurally simple, with similar properties to be found all over the world in this genre. The content of these songs is close to the child's world, presumably to make them maximally accessible children (Romet, 1980; Pond, 1981; Nograšek & Virant Iršič, 2005; Voglar & Nograšek, 2009). Meyer (1989) argues that the simplicity (in terms of structure and performance) of the genre can be explained by the influence of parameters which are external to music (e.g., ideology, social history, conditions of performance, audience, etc.).
Tonal material in children's folk songs usually covers a pitch range within a perfect fifth, and smaller, descending intervals (seconds and thirds) prevail in the melody (Borota, 2013). Proto-melodies including only two tones, a descending third G–E (so–mi), interacting with rhythmic variation, and proto-melodies using three tones from a pentatonic tetrachord (the third interval with an added fourth) are very frequently used (Gortan Carlin, Pace, & Denac, 2014).
Children's folk songs are syllabic (that is, they lack melisma), free from ornamentation, with many absolutely or relatively repeated motifs, and with minor motivic variations on account of the text (Herzog, 1944; Ling, 1997). The frequent repetition of content in this genre is due to the audience for which it is intended: repeated motifs are more readily comprehended and memorized (Borota, 2013). Duple and quadruple meter prevail over triple, and binary rhythms are preferred over ternary. The prevalence of binary relations suggests that the fundamental perceptual requirements for such relations also exist in this genre, and are intuitively deployed when creating new songs (Fraisse, 1982, explains more about binary and ternary relations).
INFORMATION DYNAMICS OF MUSIC: IDYOM
We used the computational perceptual model IDyOM 2 (Information Dynamics of Music: Pearce 2005, 2018) to measuring the (ir)regularity in children's folk songs. The model has proven to be an accurate predictor of melodic expectancy (Pearce & Wiggins, 2006a; Sauvé & Pearce, 2019), of behavior and neural measures (EEG) of melodic expectedness (Pearce et al., 2010; Agres, Abdallah, & Pearce, 2018), of phrase boundaries (Pearce, Müllensiefen, & Wiggins 2010a,b). It has been shown to provide a good quantitative model of cultural distance (Pearce, 2018).
N-gram Models
IDyOM is a computational model 3 of human melodic pitch prediction (Pearce, 2005) based on n-gram models. Such models are used effectively in the biological domain, in natural language processing, statistical machine learning, artificial intelligence, from 1950 on in music research related tasks (e.g., in machine improvisation, music information retrieval, cognitive modelling). An n-gram model is a collection of sequences, s, consisting of n symbols (characters/events), each of which is associated with a frequency count. The model calculates the probability of a symbol sn based on a history h = s1…sn-1, P(sn|h). Where n = 1, a unigram model, a zeroth–order model is determining the predictions, meaning that a symbol is independent from the previous context (symbols).
In a bigram model, n = 2, the probability of a symbol depends on just previous one, and so on. When using fixed-order n-gram models, low orders may fail to provide a good model of the global structure on the distributions, while high orders may not capture enough of the statistical regularity in a sequence. This trade-off may be addressed by using hierarchical forms of n-gram model (e.g., Wiggins & Sanjekdar, 2019), and this is arguably a necessary feature if a model is to describe the structure of sequences that include long-term dependencies (Widmer, 2016). However, IDyOM has been shown to capture the structure of melody extremely well, suggesting that such long-term dependencies are not significant in this context. A special case occurs when a Markov model encounters an unseen symbol, providing an estimated probability of zero (Pearce & Wiggins, 2006b; Wiggins, Pearce, & Müllensiefen, 2009).
These issues are addressed in IDyOM by implementing different strategies, among by extending the basic n-gram modelling to a Variable-Order Markov Model (VMM) over a finite alphabet Σ, where the conditional probability distributions are combined in a way that reflects the statistics obtained from the training data (Begleiter, El-Yaniv, & Yona, 2004). VMMs, in contrast to basic n-gram models, are able to capture contexts of different length in a single probabilistic model.
A special technique for combining the predictions of n-gram models implemented in IDyOM is the VMM lossless compression algorithm, Prediction by Partial Match (Cleary & Witten, 1984). In PPM algorithms, arithmetic coding is used to compress and decompress symbols in sequences, one symbol at a time. Predictive probability distributions P (sn|s1…sn–1) for each context in the model are calculated from frequency counts. The algorithm updates the internal model each time a symbol is encoded or decoded to improve predictions of a symbol for the remainder of the sequence (Steinruecken, Ghahramani, & MacKay, 2015).
PPM* is a version of PPM that exploit contexts of unbounded lengths. The uncertainty of the model is minimized during the prediction by estimating the distributions of all models below a variable order bound. Higher- and lower-orders predictions are combined, assigning greater weighting to higher-orders than to lower-orders, but each prediction by the model is a combination thereof (Pearce & Wiggins, 2006b). In IDyOM, predictions are generated from n-gram models of all available orders, using interpolated smoothing, with the escape mechanism, Method C, which handles events with zero value counts (Moffat, 1990).
Viewpoints
Music is multidimensional, and different musical dimensions (e.g., pitch, time, color, loudness) are not independent, but frequently interact (Prince, Thompson, & Schmuckler, 2009). Accordingly, perceptual representations of music are also multidimensional (Levitin & Tirovolas, 2009; Shepard, 1982). IDyOM's capacity to observe, to represent, to predict forthcoming events, and to manipulate multidimensional features of the musical surface, i.e., the discrete musical events at the note level (Lerdahl & Jackendoff, 1983), is afforded by the multiple viewpoint approach (Conklin, 1990a; Conklin & Witten, 1995) and further developed in the IDyOM model (Pearce, 2005).
A viewpoint allows a particular musical feature of musical events in a sequence to be observed and predicted. A musical event e is defined by a finite set of basic attributes, whose properties are specified by its type τ (e.g., pitch, duration, color, loudness). Each type τ has a syntactic domain (a set of syntactically valid elements), and a semantic domain (a set of possible meanings for elements of that type). When modelling a particular type with a viewpoint, a partial function is applied at various orders (see above), mapping sequences of events onto elements of type τ . A probability distribution of elements is generated and converted into a probability distribution of predictable elements, predicting the likelihood of each possible next event in sequence (Pearce, 2005).
IDyOM offers a range of different viewpoints which can be used in various ways, depending on the musical dimension(s) to be examined. 4 Viewpoints can be linked together: for example, viewpoints cpitch (chromatic pitch) and cpint (chromatic pitch interval) generate the linked viewpoint cpitch⊗cpint, in which an event is projected to pair of values, representing the pitch and interval of that event: thus, the type of that viewpoint is the cross-product of the types of cpitch and cpint. This allows the viewpoint system to capture the behaviors of viewpoints both individually and in combination, which in turn allows the model to be weighted dynamically, according to the strength of the correlations between viewpoints (Pearce, Conklin, & Wiggins, 2005; Hedges & Wiggins, 2016; Hedges, 2017).
Each model in IDyOM is made using a collection of viewpoints. This collection may be selected by a user, or by using an automated optimization procedure, in which hill climbing search is used to approximate the collection of viewpoints that produces the model with the lowest possible mean information content when predicting the data (this measure is sometimes called "cross-entropy": Conklin & Witten, 1995). This model is the one that represents the data with the least overall uncertainty, or which gives the most reliable predictions, given the data that is known, on average.
In the kind of music with which we are concerned, the primary dimensions are pitch and time, and these two crucial dimensions are represented in IDyOM with the basic viewpoints cpitch (chromatic pitch), dur (duration) and bioi (basic inter-onset interval). From these basic representations, derived viewpoints can be calculated, 5 following music theoretic rules. For example, cpint represents chromatic pitch interval, and cpintfref represents the chromatic pitch interval relative to the tonic of the piece (which must be given).
To explore (ir)regularity in children's folk songs in the current study, we used exactly the same viewpoints as in the previous study, because they have been shown to be relevant in the capture of (ir)regularity (Mihelač & Povh, 2020a). Specifically, we used the basic viewpoint cpitch, derived viewpoints cpint and cpintfref, and a linked viewpoint cpitch⊗dur, because currently there is still no general agreement as to whether pitch and duration are processed separately or simultaneously (Krumhansl, 2000; Jones & Boltz, 1989; Boltz, 1999; Volk, 2016). We also use the derived contour viewpoint.
Entropy, Information Content and (Ir)regularity in Children's Folk Songs
In IDyOM, the internal representations of a musical piece/style are acquired and processed by using statistical learning and probabilistic prediction. While observing and analyzing the content in a corpus consisting of musical pieces, IDyOM learns about the syntactic structure merely by exposure. On the basis of sequential regularities, the likelihood of a forthcoming event is determined from the perspective of the feature which is analyzed with a viewpoint or viewpoints (Pearce, 2005, 2018).
IDyOM simulates a listener's expectations in music (which is based on the knowledge acquired during the entire lifetime) with a long-term model (LTM), which accumulates statistical information about musical structure from a large corpus. As listeners are sensitive to repeated patterns in an on-going listening experience, a second, short-term model (STM) is also used, in which the information about the musical structure of the current piece is learned dynamically and incrementally (Pearce, 2005, 2018). LTM and STM predictions are then combined, and it has been shown that better prediction performance is achieved by combining LTM and STM dynamically (Conklin, 1990a; Pearce & Wiggins, 2004, 2006b; Pearce, 2005).
In IDyOM, two information-theoretic measures, entropy, and information content (MacKay 2003), are used for the examination of the musical content and for the prediction of events. Although these measures are fundamentally related, and have been used synonymously by Shannon and Weaver (1949), they can be considered as usefully different. Shannon's entropy, or simply entropy, related to the idea of entropy in physics, is a measure of uncertainty. It is the average number of bits, required to transmit/represent the statistical uncertainty about the character of an event, randomly selected from a probability distribution.
Less uncertainty is experienced in case when one event dominates in a probability distribution. Larger or maximum entropy is expected when no event dominates another, for example in an equal or approximately equal probability distribution. Entropy, as defined by Shannon (2001), and shown in equation 1, is used as baseline model for quantifying the uncertainty in the prediction of a musical event before it is heard, using a specific viewpoint. Hansen and Pearce (2014) provide evidence that entropy is correlated with perceived uncertainty; mathematically, it is related to the balance of likelihoods in a distribution: a uniform distribution has maximum entropy (because there is no information in the distribution) while zero (i.e., minimum) entropy entails that exactly one value of the distribution has probability 1,
where Xi is the set of all possible continuations of a given musical sequence after event ei (in our case, the alphabet of a viewpoint) and pi is the probability of event ei.
The idea behind quantifying information content (MacKay, 2003), which is significant from the perspective of compressibility (Bell, Cleary, & Witten, 1990), is to estimate how unexpected an event is in the context in which it happens. Thus, information content is a measure of unexpectedness (sometimes called "surprisal") of an event which actually appears in the sequence. For a discrete event ei, it can be calculated as shown in equation 2. Rare events in context have a low probability, are more surprising, and have a higher information content. Frequent events in context have a high probability and low information content, and so are less surprising. If the probability of an event is 1 (when there is no surprise), the information content is zero.
where pi is the probability of event ei. In the rest of this subsection, we present, as an example, the information content (unexpectedness) and entropy (uncertainty) by exploring the viewpoint cpitch in three children's folk songs, selected from the much larger dataset used in this study. Note that for each event, ei (in our case a tone in a sequence/melody), the information content and entropy is calculated from a probability distribution.
In Figure 1, the Turkish children's folk song, Cumhuriyet Çocuklarıyız, is presented. It consists of 78 events, in which motifs, hereafter defined as patterns (p), are denoted by p1, p2, and p3. From the perspective of pitch span (within a perfect fifth), rhythm, and meter, the song is simple. Furthermore, the song has a clear and understandable musical syntax, and with a structure that is strong, consisting of three dominant and often at pitch repeated patterns with substantial relationships, as p2 always follows p1, and p3 follows p2. Below we introduce algorithm Ir_Reg to classify songs into regular and irregular based on the mean values of the viewpoints computed by IDyOM. This algorithm classifies this song (Cumhuriyet Çocuklarıyız) as "regular" and therefore complies with our observations.

Figure 1. An example of a regular, structured melody. The Turkish children's folk song Cumhuriyet Çocuklarıyız, consists of three at pitch repeated patterns (the patterns are marked with p), which are repeated throughout the entire song. From the perspective of their frequency of appearance, these patterns can be considered as "recurrent", "dominant", and the melody appears to be "regular".
In Table 1, the information content (IC), and entropy (E), obtained for the viewpoint cpitch, and assigned to each event in pattern p1 is shown. The pattern p1 appears at the beginning of the song (from e1 to e4), and is repeated four times, in e25–28, e35–38, e59–62, and e69–72. The order of the events (from e1 to e4) is always the same, which means, that each repeated version of pattern p1 starts with the same note presented as event e1, and afterwards as e25, e35, e59, and e69 in the repeated patterns.
| Event | 1st (IC/E) | Event | 2nd (IC/E) | Event | 3rd (IC/E) | Event | 4th (IC/E) | Event | 5th (IC/E) |
|---|---|---|---|---|---|---|---|---|---|
| e1 | 3.62/3.87 | e25 | 3.96/2.56 | e35 | 2.90/2.50 | e59 | 1.24/2.38 | e69 | 1.05/2.20 |
| e2 | 1.91/3.60 | e26 | 2.44/2.76 | e36 | 2.88/1.80 | e60 | 1.05/2.29 | e70 | 1.04/2.20 |
| e3 | 2.99/3.37 | e27 | 1.66/2.62 | e37 | 2.05/2.42 | e61 | 1.41/2.29 | e71 | 1.43/2.30 |
| e4 | 0.56/1.62 | e28 | 0.51/1.66 | e38 | 0.44/1.52 | e62 | 0.37/1.38/ | e72 | 0.33/1.27 |
Note. The IC values in the first and second appearance of this pattern are more or less similar, but then decrease in the third, fourth, and fifth appearance.
Tables 2 and 3 present the IC and E values for pattern p2 and p3, respectively. As in pattern p1 the events in these two patterns always appear in the same order in the repeated versions. A tendency to decrease is visible in the IC of the events in all three patterns (depicted also in Figure 2), from their first to their last (repeated) appearance.
| Event | 1st (IC/E) | Event | 2nd (IC/E) | Event | 3rd (IC/E) | Event | 4th (IC/E) | Event | 5th (IC/E) |
|---|---|---|---|---|---|---|---|---|---|
| e5 | 1.42/2.13 | e29 | 1.20/2.09 | e39 | 0.63/1.62 | e63 | 0.62/1.65 | e73 | 0.45/1.37 |
| e6 | 6.89/1.51 | e30 | 2.03/2.44 | e40 | 1.85/2.05 | e64 | 0.69/1.82 | e74 | 0.57/1.68 |
| e7 | 2.35/3.02 | e31 | 1.74/2.47 | e41 | 0.97/2.12 | e65 | 0.73/1.87 | e75 | 0.59/1.68 |
| e8 | 2.16/2.79 | e32 | 1.09/2.35 | e42 | 0.74/1.96 | e66 | 0.59/1.74 | e76 | 0.49/1.57 |
| e9 | 1.81/2.14 | e33 | 0.98/2.07 | e43 | 0.68/1.78 | e67 | 0.54/1.58 | e77 | 0.45/1.42 |
| e10 | 6.16/2.45 | e34 | 1.67/2.54 | e44 | 0.89/2.10 | e68 | 0.66/1.83 | e78 | 0.53/1.63 |
Note. The IC values and entropy values in this pattern decrease after its first appearance in each further repetition.
| Event | 1st (IC/E) | Event | 2nd (IC/E) | Event | 3rd (IC/E) | Event | 4th (IC/E) |
|---|---|---|---|---|---|---|---|
| e11 | 4.13/2.94 | e18 | 4.78/2.54/ | e45 | 2.03/2.41 | e52 | 1.56/2.46 |
| e12 | 1.65/2.67 | e19 | 1.81/2.72 | e46 | 1.03/2.19 | e53 | 0.92/2.17 |
| e13 | 1.51/2.33 | e20 | 1.28/2.45 | e47 | 0.58/1.69 | e54 | 0.43/1.45 |
| e14 | 2.16/1.97 | e21 | 1.46/2.34 | e48 | 0.84/1.98 | e55 | 0.60/1.75 |
| e15 | 1.63/2.04 | e22 | 1.37/2.04 | e49 | 0.80/1.82/ | e56 | 0.63/1.70 |
| e16 | 3.74/2.06 | e23 | 2.28/2.39 | e50 | 0.89/2.06 | e57 | 0.64/1.79 |
| e17 | 2.53/2.54 | e24 | 1.53/2.52 | e51 | 0.88/2.08 | e58 | 0.67/1.83 |
Note. The IC values in this pattern (exception is the second repetition compared to the first appearance) decreases, as in pattern p2, with each new repetition.
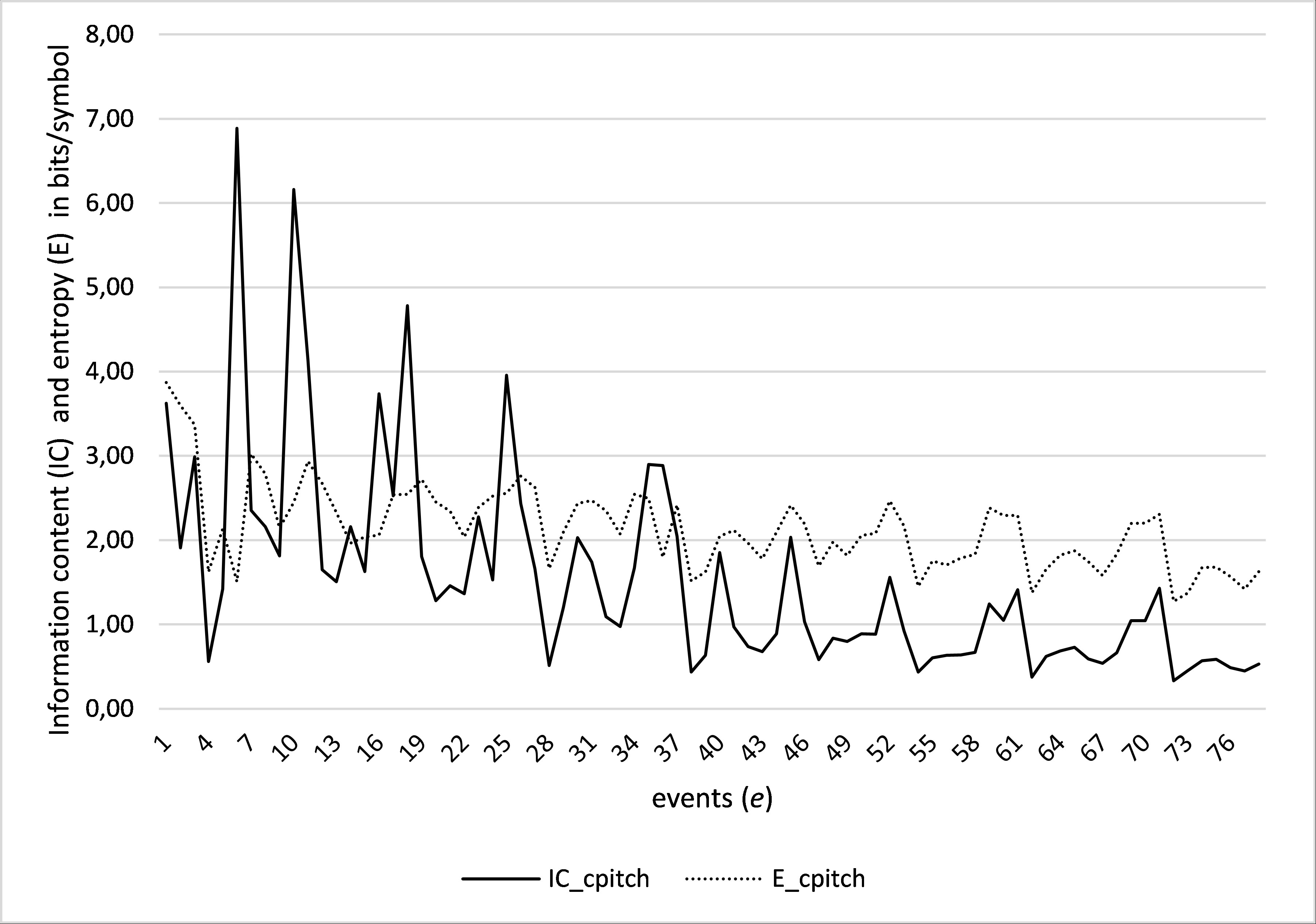
Figure 2. Information content (IC) and entropy (E) for the viewpoint cpitch in the Turkish children's folk song Cumhuriyet Çocuklarıyız. Both values decrease through this song. The peaks in the graph (event e6, e10, e18, and e25), correspond with notes with low-probability.
The second song, Schneeglöggli, which is from Switzerland (see Figure 3) consists of 50 events and 11 patterns, again labeled as pi.

Figure 3. An example of a structure with weak relationships between the patterns (motifs). This Swiss children's folk song Schneeglöggli has even 11 motifs, and none of them is dominant, repeated at pitch or transposed repeated, therefore giving the impression of an irregular, non-structured melody.
Ir_Reg classifies this song as "irregular". It has a weak structure, without any dominant (repeated at pitch or transposed repeated) patterns, and it has large intervals (e.g., event e35–36) and no special relations between the patterns. The information content (IC) and entropy (E) obtained for the viewpoint cpitch are presented for each event in this song in Figure 3 (in the musical score, in the boxed text IC and E) and depicted also in Figure 4. We can see clearly very high IC values in each of the 11 patterns, giving the impression of highly unexpected and complex musical content.
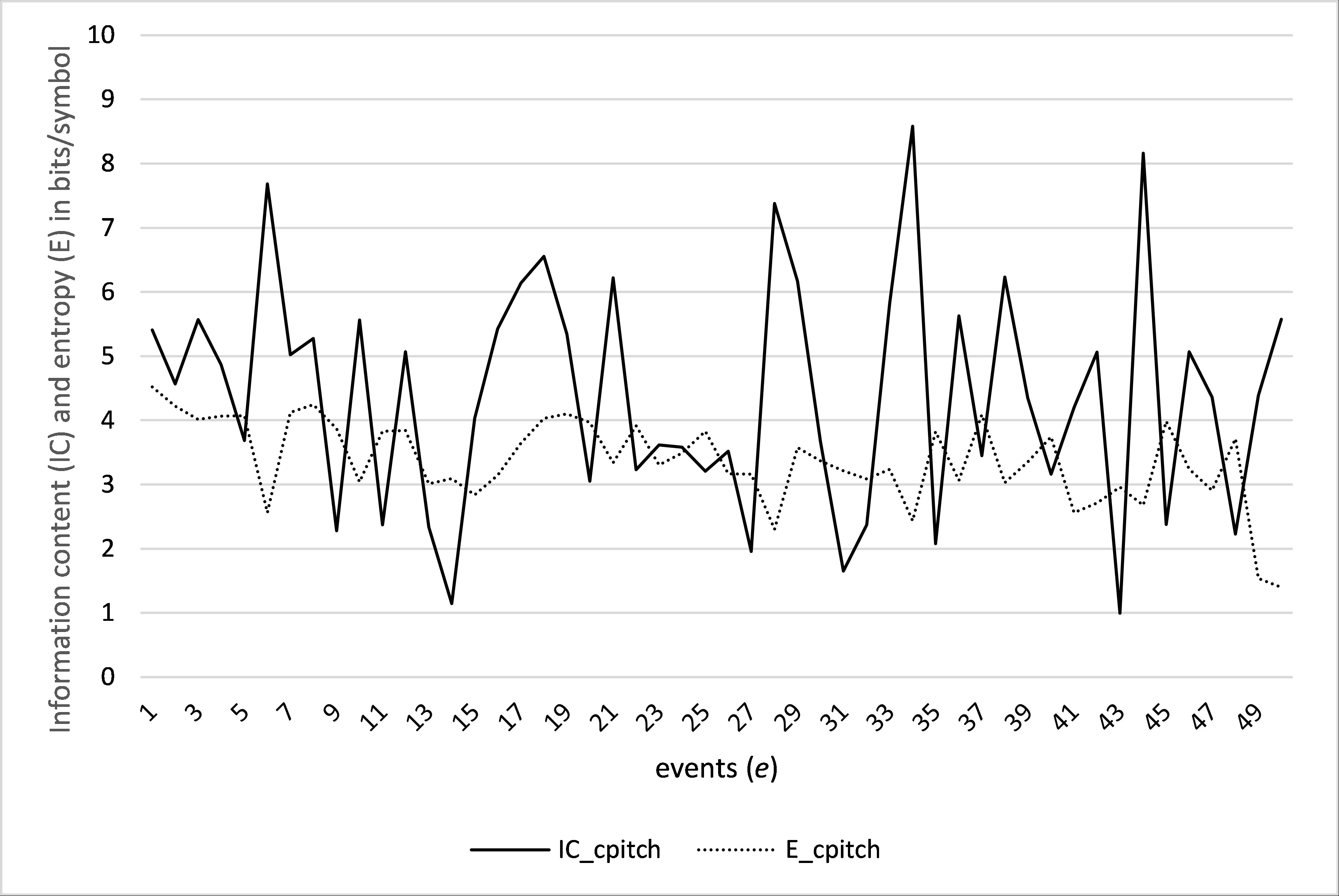
Figure 4. Information content (IC) and entropy (E) obtained for the viewpoint cpitch in the Swiss children's song Schneeglöggli. The entropy values (E) are slightly decreasing. The values for the information content remain very high, showing that the events in this song are highly unexpected.
The third song, Doidas andam as galinhas, from Portugal (Figure 5), has been classified by Ir Reg as "neutral".

Figure 5. An example with transposed repeated patterns in the Portuguese children's folk song Doidas andam as galinhas.
The song consists of 48 events with three distinct patterns (p1, p2, p3), and three transposed repeated patterns, of which the pattern t1 is a transposed repetition of pattern p1, t2 a transposed repetition of pattern p2, and pattern t3, a transposed repetition of pattern p3. As can be seen in Figures 5 and 6, the information content of the patterns t1, t2, and t3 suggests that the content of these patterns is perceived as unexpected, even though they are a transposed repetition of the three main patterns.

Figure 6. Information content (IC) and entropy (E) obtained for the viewpoint cpitch in the Portugal children's song Doidas andam as galinhas
Table 4 presents the mean values for information content and entropy (the mean value across all the events in a particular song), for each viewpoint (ten variables) and the three example songs separately. The mean values of IC and E are taken as a measure of (ir)regularity: songs with a high IC and E, are classified as more irregular than those with low values.
| Viewpoint | Cumhuriyet Çocuklarıyız |
Doidas andam as galinhas |
Schneeglöggli |
|---|---|---|---|
| (regular) | (neutral) | (irregular) | |
| IC_cpitch | 1.36 | 2.46 | 4.40 |
| E_cpitch | 1.99 | 2.49 | 3.37 |
| IC_cpint | 1.70 | 2.12 | 3.73 |
| E_cpint | 2.12 | 2.41 | 3.03 |
| IC_cpintfref | 2.05 | 3.15 | 3.83 |
| E_cpintfref | 2.61 | 3.18 | 3.68 |
| IC_cpitch⊗dur | 1.46 | 2.81 | 4.80 |
| E_cpitch⊗dur | 1.78 | 2.41 | 3.24 |
| IC_contour | 4.15 | 4.02 | 4.96 |
| E_contour | 3.68 | 3.72 | 3.90 |
THE DETECTION AND PREDICTION OF (IR)REGULARITY IN CHILDREN'S FOLK SONGS BY IR_REG
Data
The data used in this paper consists of 736 monophonic children's folk songs from 22 European countries (see Table 5), and is available at https://github.com/LMihel/LMihel.github.io. The decision to include Russia in this data is geographical (about 23% of the western part of Russia can be considered as a part of Europe), and historical, political, and cultural, due to the connection between former and present Russia with Europe (Graney, 2019). Turkey has been added to this data because of the fact that a small part (roughly 3%) is considered from the geographic perspective as Europe, and because of a shared historical, political, and cultural background with different European countries during the Ottoman Empire (Hurewitz, 1961; Kostopoulou, 2016).
A selection of children's folk songs from Germany was obtained from the Essen Folksong Collection (Schaffrath, 1995). The selection of Dutch children's folk songs has been obtained from the Meertens Tune Collection (The Meertens Tune Collections, 2019). Children's folk songs from 20 other countries have been collected by the authors from various books, containing traditional (children's) folk songs, provided by the courtesy of national/school libraries from these countries.
From these 20 countries, we selected only children's folk songs, which were included either in the formal music syllabus or in song books used as additional educational material in kindergartens and primary schools. Furthermore, wherever possible, we have included children's folk songs whose origin is in a certain country (although the same song can often be found in another country, even in European countries which are geographically widely separated e.g., a "wanderer melody" found in the Czech song Kočka leze dírou, pes oknem, and in the Slovenian song čuk se je oženil).
| Country | Num. of songs |
Country | Num. of songs |
|---|---|---|---|
| Bulgaria | 18 | Croatia | 16 |
| Denmark | 15 | France | 71 |
| Germany | 124 | Great Britain | 38 |
| Greece | 26 | Hungary | 27 |
| Italy | 22 | Latvia | 23 |
| Netherlands | 58 | Norway | 23 |
| Poland | 22 | Portugal | 27 |
| Romania | 18 | Russia | 21 |
| Serbia | 13 | Slovenia | 44 |
| Spain | 54 | Sweden | 29 |
| Switzerland | 23 | Turkey | 24 |
Algorithm Ir Reg
We now describe our algorithm Ir_Reg. Ir_Reg takes as an input two sets of songs: the entire data set D, a subset D̅ of D, and a set V of viewpoints that we want to analyze. Firstly, Ir_Reg computes by IDyOM information content and entropy for all viewpoints from V, for all songs from D̅, using the entire data set D. Next, Ir_Reg calculates the maximum values of these viewpoints across the dataset D̅. Finally, for each song from the subset D̅ the algorithm counts the number of viewpoints above the 75% of the maximum value of the viewpoint (upper threshold) or below the 25% of the maximum value of the viewpoint (lower threshold). The Ir_Reg algorithm is actually defined for general set of information content and entropy viewpoints V, but in this paper, it was applied with V consisting of {cpitch, cpint, cpintfref, cpitch⊗dur, and contour}.
If a given song has at least 5 values (entropy or information content) above the upper threshold it is classified as irregular. Otherwise, if it has at least 5 values below the lower threshold, it is classified as regular. If neither of these cases happens, it is labeled as unclassified. The number 5 in the algorithm was determined empirically. Ir_Reg is specified below as Algorithm 1.
Results
In order to analyze the (ir)regularity of the musical structure in our data, we firstly analyzed the entire data (736 children's folk songs) by examining the information content and entropy of each of the set of viewpoints V, as explained above. In other words, we ran Ir_Reg with input data sets D (the entire data set) and D̅ = D. For each song from D we computed by IDyOM the mean values of IC_cpitch, E_cpitch, IC_cpint, E_pint, IC_cpintfref, E_cpintfref, IC_cpitch⊗dur, E_cpitch⊗dur, IC_contour, and E_contour.
Then we classified the songs as regular, irregular, or unclassified using the global threshold values (i.e., the values computed across D) and counted the numbers of songs that were classified as regular, irregular, or unclassified, for each country separately. These totals are presented in Table 6 and visualized on Figure 7. Regarding the relative frequencies, the most irregular in the structure are the songs from Norway, since 17 out of 23 (74%) are classified as irregular. The most regular songs are the songs from Serbia, where 11 songs out of 13 (85%) were labelled as regular. Other countries with no regular songs in our dataset are Switzerland and Great Britain, while the countries with no irregular songs are Croatia, Hungary, Portugal, Romania, and Turkey.
| Country | Irregular | Regular | Unclassified | Country | Irregular | Regular | Unclassified |
|---|---|---|---|---|---|---|---|
| Bulgaria | 2 | 3 | 13 | Croatia | 0 | 12 | 4 |
| Denmark | 4 | 2 | 9 | France | 16 | 9 | 46 |
| Germany | 16 | 28 | 80 | Great Britain | 23 | 0 | 15 |
| Greece | 3 | 10 | 13 | Hungary | 0 | 12 | 15 |
| Italy | 3 | 6 | 13 | Latvia | 2 | 4 | 17 |
| Netherlands | 6 | 14 | 38 | Norway | 17 | 0 | 6 |
| Poland | 1 | 5 | 16 | Portugal | 0 | 8 | 19 |
| Romania | 0 | 5 | 13 | Russia | 4 | 5 | 12 |
| Serbia | 0 | 11 | 2 | Slovenia | 8 | 7 | 29 |
| Spain | 16 | 13 | 25 | Sweden | 17 | 2 | 10 |
| Switzerland | 18 | 0 | 5 | Turkey | 0 | 16 | 8 |
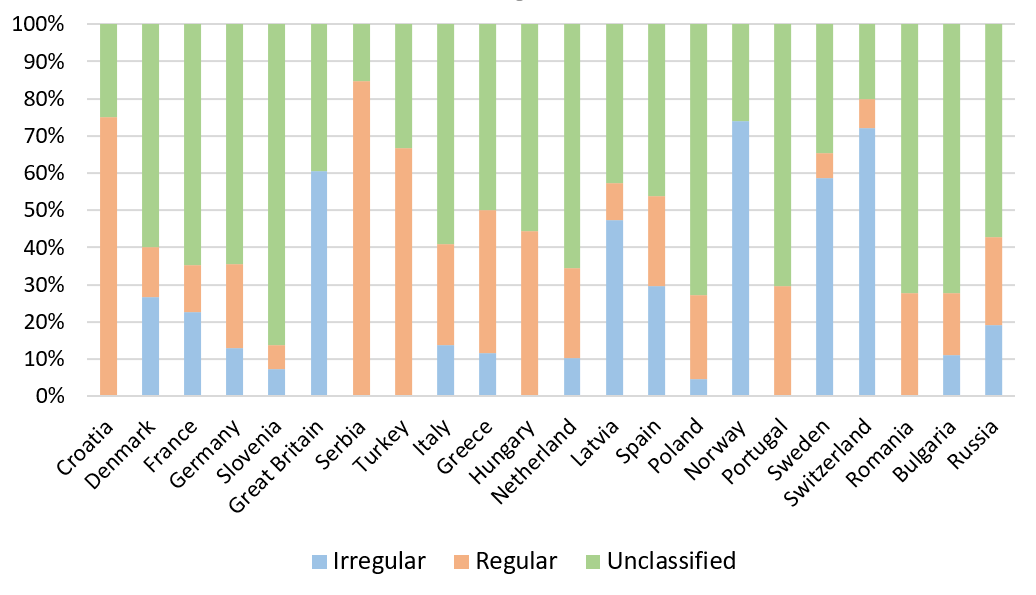
Figure 7. The percentage of irregular, regular, and unclassified children's folk songs in each country. Total number of children's folk songs is 736.
| Irregular | Regular | Unclassified | Treshold | Treshold | |
|---|---|---|---|---|---|
| Viewpoint | (mean) | (mean) | (mean) | (25%) | (75%) |
| IC_cpitch | 3.06 | 1.84 | 2.37 | 2.00 | 2.72 |
| E_cpitch | 2.79 | 2.41 | 2.61 | 2.45 | 2.75 |
| IC_cpint | 3.07 | 1.97 | 2.49 | 2.13 | 2.82 |
| E_cpint | 2.66 | 2.41 | 2.57 | 2.40 | 2.71 |
| IC_cpintfref | 3.45 | 2.61 | 3.04 | 2.71 | 3.73 |
| E_cpintfref | 3.39 | 3.15 | 3.30 | 3.05 | 3.57 |
| IC_cpitch⊗dur | 3.17 | 1.77 | 2.41 | 1.93 | 2.87 |
| E_cpitch⊗dur | 2.71 | 2.18 | 2.43 | 2.21 | 2.63 |
| IC_contour | 4.23 | 3.63 | 3.86 | 3.51 | 4.27 |
| E_contour | 3.60 | 3.48 | 3.50 | 3.32 | 3.73 |
We also performed principal component analysis (PCA) with the same variables. Figure 8 shows irregular, regular and unclassified children's folk songs, projected to the 2-dimensional subspace spanned by the first two principal components, of which the first explains 54,7% variance, and the second explains 18.4% of total variance. We can actually observe that these three groups could be well separated also using only the first principal component.
Table 8 contains data about importance of the principal components. We can see that we need 5 principal components to explain 94 % of variability (conventional goal in PCA is 95%), which reveals that the data has 5 important dimensions.

Figure 8. Visualization of irregular, regular, and unclassified children's folk songs with the first two principal components.
| Component | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 | PC9 | PC10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Standard deviation | 2.34 | 1.36 | 1.01 | 0.82 | 0.63 | 0.42 | 0.41 | 0.33 | 0.28 | 0.25 |
| Proportion of Variance | 0.55 | 0.18 | 0.10 | 0.07 | 0.04 | 0.02 | 0.02 | 0.01 | 0.01 | 0.01 |
| Cumulative Proportion | 0.55 | 0.73 | 0.83 | 0.90 | 0.94 | 0.96 | 0.97 | 0.99 | 0.99 | 1.00 |
Secondly, we analyzed the (ir)regularity of the musical structure in data from each country separately by examining the information content and entropy with the same viewpoints, and by applying our algorithm to our data sets of songs from each country. Therefore, we ran Ir_Reg for each country separately with the inputs D – the entire dataset, and D̅– the dataset of songs from particular country. More precisely, we took the values of viewpoints, computed across the whole data set D, but the threshold values were computed using only the viewpoints from the songs of particular country D̅. These threshold values were basis for classification of songs from D̅. This gave as a new classification, presented in Table 9. In total, from 736 children's folk songs, we detected with this approach 158 irregular and 173 regular children's folk songs.
| Country | Irregular | Regular | Unclassified | Country | Irregular | Regular | Unclassified |
|---|---|---|---|---|---|---|---|
| Bulgaria | 5 | 3 | 10 | Croatia | 4 | 4 | 8 |
| Denmark | 3 | 4 | 8 | France | 15 | 16 | 40 |
| Germany | 29 | 27 | 68 | Great Britain | 7 | 10 | 21 |
| Greece | 5 | 8 | 13 | Hungary | 6 | 5 | 16 |
| Italy | 6 | 7 | 9 | Latvia | 3 | 4 | 16 |
| Netherlands | 12 | 16 | 30 | Norway | 5 | 4 | 14 |
| Poland | 3 | 5 | 14 | Portugal | 3 | 7 | 17 |
| Romania | 4 | 5 | 9 | Russia | 3 | 6 | 12 |
| Serbia | 3 | 3 | 7 | Slovenia | 11 | 10 | 23 |
| Spain | 11 | 11 | 32 | Sweden | 7 | 8 | 14 |
| Switzerland | 7 | 5 | 11 | Turkey | 6 | 5 | 13 |
In these 331 children's folk songs, we analyzed, with two additional and independent musical experts, patterns (motifs) by using the musical score. Each pattern (p), either repeated at pitch or transposed repeated (t), was firstly annotated in the musical score. Secondly, based on the frequency distribution of patterns in each song, we computed the entropy of unigrams for each song (Mihelač & Povh, 2020b give details about computing the unigrams). The Welch two-samples t-test was used to compare the difference in mean values of unigrams between the irregular and regular children's folk songs. The difference is statistically significant, (p < 6.651e-11), i.e. the mean value of unigram was significantly smaller on the set of on regular children's folk songs, mainly because the transposed repeated patterns were more recurrent in regular children's folk songs compared to irregular.
A chi-square test of independence was performed to examine the relation between transposed repeated patterns (t) and the (ir)regularity in musical structure. More precisely, we considered only the classified songs (i.e., regular, and irregular) and have introduced new binary variable having value 1 if the song contained transposed repeated patterns (t) and 0 otherwise. The relation between these two variables was significant, X2(1, N=331) = 27.09, p = 1.942e-07, which means that transposed repeated patterns were more frequent in the irregular children's folk songs (in 80 songs out from 158) than in regular one (only in 39 songs out from 173).
Implied harmony was examined with IC_cpintfref and E_cpintfref (Table 7) and analyzed in musical score. In Table 7, we see that no significant differences were found between irregular and regular children folk songs. The majority of the children's folk songs start with the tonic triad as its first chord, and ends with the tonic triad. However, dominant triads were found in some songs (0.68%), even subdominant triads (0.41%) at the beginning of the songs, and dominant (1.49%), and subdominant (0.13%) triads in the endings (Table 10).
| Beginning of songs | Ending of songs | ||
|---|---|---|---|
| dominant triad | subdominant triad | dominant triad | subdominant triad |
| 0.68 % | 0.41 % | 1.49 % | 0.13 % |
DISCUSSION AND CONCLUSIONS
A plausible explanation for a higher or lower presence of (ir)regular songs in some countries could be that children's folk songs exist in each of the 22 countries, whose origin can be traced to folk songs. Folk songs are a true amalgam of different historical, cultural, and musical processes (Golež Kaučič, 2003), carrying thus all the specificities of a (musical) culture from a particular country. This means that all the diversity found in folk songs, passed to the children population due to its (suitable) content, presumably without simplifying the musical structure, either from the perspective of musical dimensions, or musical elements, can be found also in children's folk songs. This could clarify either a very high or low information content and entropy found in children's folk songs in some countries.
According to our results, frequency of repeated patterns contributes to a more regular musical structure and to a stronger feeling of regularity, if the patterns are repeated at pitch, which is in accordance with the findings from Bader, Schröger, and Grimm (2017), although even transposed repeated forms (in our case transposed repeated patterns) can be perceived as different, depending on the context which precede or follow it (Margulis, 2014, p. 27–54). Musical structure is perceived as more regular, if the recurrence of a pattern is not "masked" (see more about it in the study from Bruner, Wallach, & Galanter, 1959), as it was the case with the transposed repeated patterns found in irregular and regular children's folk songs.
It seems that the perception of these relative repeated patterns is affected somehow by the duration of children's folk songs, which are approximately 8–12 bars long. If the children's folk songs were longer, the transposed repeated patterns could have a more significant role in the identification of these patterns as a transposed repetition of patterns repeated at pitch, and contribute more significantly to the regularity of the musical structure (more about the significance of repetition in longer musical pieces in the studies from Deliège, 1987; Cambouropoulos, Crawford, & Iliopoulos, 2001). As the duration of a children's folk songs is on average short, then the mixture of patterns repeated at pitch and transposed repeated patterns in a very short time period is actually interfering with the recurrent regularities, i.e., it is not contributing to a more regular structure, but rather to more noise, which is in accordance with the findings of Bruner, Wallach, & Galanter (1959).
The principal component analysis (PCA) performed on all the variables (IC_cpitch, E_cpitch, IC_cpint, E_cpint, IC_cpintfref, E_cpintfref, IC_cpitch⊗dur, E_cpitch⊗dur, IC_contour, E_contour), has shown that regular and irregular musical songs were linearly separated into a 2-dimensional subspace spanned by the first two principal components. The salience of pitch in the perception of (ir)regular structure, can be understood, that each pitch, even when being acoustically identical to another one, can be perceived as different, depending on the context, as each pitch can differ in its tonal function, i.e., each pitch can have assigned a unique function in two different tonalities (Krumhansl & Shepard, 1979).
Small pitch intervals are prevailing in children's folk songs, as also in a considerable number of folk songs across the world (Huron, 2001; Von Hippel, 2000), of which some, included in our data, were found to exist as children's folk songs in different countries. Some of these folk/children's folk songs in the data were assigned as extremely irregular and complex (especially the songs from Great Britain, Norway, and Switzerland, according to our results), not only because of highly unexpected distributions of pitch in the melody, but also because of the use of large leaps (intervals) between successive notes. Thus, not only pitch, but also pitch intervals are affecting the regularity of a musical structure, which was found also in the study of Beauvois (2007).
Differences in rhythm (duration) were found between irregular and regular children's folk songs (see Table 7). The regularity in metrical structure, is according to different studies affected by the absence/presence of a regular beat, which groups different rhythms in time intervals (Bouwer et al., 2018). However, with the exception of some children's folk songs found in e.g., Bulgaria, Romania and Turkey, the in-depth analysis of the musical scores showed that rhythm, based on recurring pulse/meter was found more or less in the majority of children's folk songs included in our data. Recurrent pulse/meter has obviously contributed to a more regular musical structure, in which the events are more predictable, which is also in accordance with the findings in the study of Lappe, Steinsträter, & Pantev (2013).
No significant impact on regularity was found in the analysis of (implied) harmony examined with IC_cpintfref and E_cpintfref (Table 7). This result was expected, as basic harmonic progressions are prevalent in the melodies, either in irregular or regular children's folk songs (e.g., progressions I-V-I, I-IV-V-I, I-IV-I, …). The use of dominant/subdominant functions and triads at the beginning and end of songs is to be understood more as a rare exception rather than a rule in children's folk songs. Furthermore, three basic harmonic functions (tonic, dominant, subdominant) are predominantly found in children's folk songs (Berget, 2017), suggesting that harmony, as a secondary parameter, is in this genre established and heavily dependable on the syntactical constraints and rules formed by the primary parameter pitch (see more about primary and secondary parameters in Meyer, 1989, and Bauer, 2001).
Contour has not been shown to affect the regularity of the musical structure in children's folk songs (Table 7). A plausible explanation could be that the information about contour is present in other viewpoints (for example in cpitch and cpint). Furthermore, in the majority of children's folk songs, ascending and descending directions of the melodies (arch-like structure) have been found. This is probably related to the origins of some children's folk songs traced to folk songs with an arch-like melody. The same tendency of ascending-descending (convex) melodies has been found in a computerized analysis from Huron (1996) in 40% of approximately 10,000 phrases (5–11 notes in length), and also in combined phrases (two phrases together, with a low midpoint, producing an overall convex shape) in over 6000 European folk songs. Furthermore, contour has proven to be a powerful identifying factor in melodic recognition, and to contribute to a better memorization of melodies (Dowling, 1978; Bartlett & Dowling, 1980; Trainor & Trehub, 1993; Trehub, Bull, & Thorpe, 1984), which could also explain the prevailing arch-shaped contour in children's folk songs, which is more or less predictable and probably contributing to a higher feeling of regularity.
In this study, we have shown that irregularity exists in children's folk songs, and that this genre can be complex. Future research with additional examples of children's folk songs in each country, and with more musical feature variables in defining (ir)regular songs could extend the explanations of (ir)regularity. An in-depth analysis of the origin of children's folk songs would certainly contribute to the understanding of (ir)regularities found in the musical structure of this genre, and why irregular structure is more frequently found in some European countries than in other European countries.
ACKNOWLEDGEMENTS
This research work was supported by Šolski center Novo Mesto, Slovenia, by the Slovenian Research Agency (ARRS) through the research project J1-8155, and partially supported by a sabbatical grant from IJS.
NOTES
- An example is the transposition of a fragment where only the pitch intervals in a part are repeated, while the entire fragment is shifted in pitch.
Return to Text - IDyOM may be downloaded from https://github.com/mtpearce/idyom/wiki
Return to Text - The word "model" has been used in this paper as a term for the IDyOM 'theory-and-system', and also for some of its components (models of data).
Return to Text - http://mtpearce.github.io/idyom/ gives an exhaustive list.
Return to Text - A full list of the available viewpoints is given on the IDyOM website, http://mtpearce.github.io/idyom/
Return to Text
REFERENCES
- Agres, K. R. (2019). Change detection and schematic processing in music. Psychology of Music 47(2), 173–193. https://doi.org/10.1177/0305735617751249
- Agres, K. R, Abdallah, S. & M T Pearce, M. T. (2018). Information-Theoretic Properties of Auditory Sequences Dynamically Influence Expectation and Memory. Cognitive Science 42(1), 43–76. https://doi.org/10.1111/cogs.12477
- Bader, M., Schröger, E., & Grimm, S. (2017). How regularity representations of short sound patterns that are based on relative or absolute pitch information establish over time: An EEG study. https://doi.org/10.1371/journal.pone.0176981
- Bangert, M., & Altenmüller, E. (2003). Mapping perception to action in piano practice: a longitudinal dc-eeg study. BMC Neuroscience 4(26), 1-14. https://doi.org/10.1186/1471-2202-4-26
- Bartlett, J. C., & Dowling, W. J. (1980). Recognition of transposed melodies: A key-distance effect in developmental perspective. Journal of Experimental Psychology: Human Perception and Performance 6, 501–515. https://doi.org/10.1037/0096-1523.6.3.501
- Bauer, A. (2001). Composing the sound itself: secondary parameters and structure in the music of Ligeti. Indiana Theory Review 22(1), 37–64.
- Beauvois, M. W. (2007). Quantifying aesthetic preference and perceived complexity for fractal melodies. Music Perception: An Interdisciplinary Journal 24(3), 247–264. https://doi.org/10.1525/mp.2007.24.3.247
- Begleiter, R., El-Yaniv, R., & Yona, G. (2004). On prediction using variable order Markov models. Journal of Artificial Intelligence Research 22, 385–421. https://doi.org/10.1613/jair.1491
- Bell, T. C., Cleary, J. G., & Witten, I. H. (1990). Text Compression. Englewood Cliffs, NJ: Prentice Hall, USA.
- Berezovsky, J. (2019). The structure of musical harmony as an ordered phase of sound: A statistical mechanics approach to music theory." Science Advances 5(5). Retrieved from https://doi.org/10.1126/sciadv.aav8490
- Berget, G. E. (2017). Using Hidden Markov Models for Musical Chord Prediction. Master's thesis, Norwegian University of Science and Technology, Norway.
- Bharucha, J. J., & Stoeckig, K. (1986). Reaction time and musical expectancy: Priming of chords. Journal of Experimental Psychology: Human Perception and performance 5, 403–410. https://doi.org/10.1037/0096-1523.12.4.403
- Bigand, E., Delbé, C., Poulin-Charronnat, B., Leman, M., & Tillmann, B. (2014). Empirical evidence for musical syntax processing? Computer simulations reveal the contribution of auditory short-term memory. Frontiers in Systems Neuroscience 8, 94. https://doi.org/10.3389/fnsys.2014.00094
- Bigand, E., & Poulin-Charronat, B. (2006). Are we experienced listeners? A review of the musical capacities that do not depend on formal musical training. https://doi.org/10.1016/j.cognition.2005.11.007
- Blacking, J. (1973). How Musical is Man? Seattle, London: University of Washington Press, USA.
- Boltz, M. G. (1999). The processing of melodic and temporal information: independent or unified dimensions? Journal of New Music Research 28, 67–79. https://doi.org/10.1076/jnmr.28.1.67.3121
- Borota, B. (2013). Osnove teorije glasbe in oblikoslovja za učitelje in vzgojitelje. Univerzitetna založba Annales Koper, Slovenia.
- Bouwer, F. L., Burgoyne, J. A., Odijk, D., Honing, H., & Grahn, J. (2018). What makes a rhythm complex? The influence of musical training and accent type on beat perception. https://doi.org/10.1371/journal.pone.0190322
- Brailoiu, C. (1954). Le rythme enfantin. Colloques de Wegimonts, Cercle International d'Etude Ethnomusicologique, Brussels, 64–96.
- Bruner, J. S., Wallach, M. A., & Galanter, E. H. (1959). The Identification of Recurrent Regularity. The American Journal of Psychology 72(2), 200–209. https://doi.org/10.2307/1419364
- Cambouropoulos, E., Crawford, T., & Iliopoulos, C. S. (2001). Pattern Processing in Melodic Sequences: Challenges, Caveats and Prospects. Computers and the Humanities 35, 9–21. https://doi.org/10.1023/A:1002646129893
- Campbell, P. S. (1998). Songs in Their Heads: Music and Its Meaning in Children's Lives. Oxford University Press, UK.
- Cleary, J. G., & Witten, I. (1984). Data compression using adaptive coding and partial string matching. IEEE Transactions on Communications 32, 396–402. https://doi.org/10.1109/TCOM.1984.1096090
- Cohen, D. (2003). Perception and Responses to Schemata in Different Cultures: Western and Arab Music. In Proceedings of the 5th Triennial ESCOM Conference, 519–522.
- Cohen, D., & Katz, R. L. (2013). Toward a Musical Analysis of World Music. Israel Studies in Musicology Online 13(1), 1-38.
- Conklin, D. (1990a). Prediction and Entropy of Music. Master's thesis, Department of Computer Science, University of Calgary, Canada.
- Conklin, D., & Witten, I. H. (1995). Multiple viewpoint systems for music prediction. Journal of New Music Research 24(1), 51–73. https://doi.org/10.1080/09298219508570672
- Deliège, I. (1987). Grouping conditions in listening to music: An approach to Lerdahl and Jackendoff's grouping preference rules. Music Perception 4, 325–360. https://doi.org/10.2307/40285378
- Deutsch, D. (1980). The processing of structured and unstructured tonal sequences. Gestalt perception in music. Perception & Psychophysics 28, 381–389. https://doi.org/10.3758/BF03204881
- Dowling, W. J. (1978). Scale and Contour: Two Components of a Theory of Memory for Melodies. Psychological Review 85(4), 341–354. https://doi.org/10.1037/0033-295X.85.4.341
- Fitch, W. T. (2006). The biology and evolution of music: A comparative perspective. Cognition 100, 173–215. https://doi.org/10.1016/j.cognition.2005.11.009
- Fraisse, P. (1982). Rhythm and tempo. In D. Deutsch (Ed.), The psychology of music, (pp.149–180). Orlando, FL: Academic Press. https://doi.org/10.1016/B978-0-12-213562-0.50010-3
- Garner, W. R. (1974). The processing of information and structure. Potomac, MD: Erlbaum, USA.
- Godt, I. (2005). Music: A practical definition. The Musical Times 146(1890), 83–88. https://doi.org/10.2307/30044071
- Golež Kaučič, M. (2003). Ljudsko in umetno. Dva obraza ustvarjalnosti. Ljubljana: Založba ZRC, Slovenia.
- Gortan-Carlin, I. P., Pace, A., & Denac, O. (2014). Glazba i tradicija: izabrani izričaji u regiji Alpe-Adria. Sveučilište Jurja Dobrile u Puli, Croatia.
- Grahn, J. A., & Rowe, J. B. (2012). Finding and Feeling the Musical Beat: Striatal Dissociations between Detection and Prediction of Regularity. Cerebral Cortex 23(4), 913–921. https://doi.org/10.1093/cercor/bhs083
- Graney, K. (2019). Russia, the Former Soviet Republics, and Europe since 1989. Oxford, University Press, UK. https://doi.org/10.1093/oso/9780190055080.001.0001
- Hansen, N. Chr., & Pearce, M. T. (2014). Predictive uncertainty in auditory sequence processing. Frontiers in Psychology 5: 1052. https://doi.org/10.3389/fpsyg.2014.01052
- Hedges, T., & Wiggins, G. A. (2016). The Prediction of Merged Attributes with Multiple Viewpoint Systems. Journal of New Music Research 45(4), 314–332. https://doi.org/10.1080/09298215.2016.1205632
- Hedges, T. W. (2017). Advances in Multiple Viewpoint Systems and Applications in Modelling Higher Order Musical Structure. Ph.D. thesis, Queen Mary University of London, UK.
- Herzog, G. (1944). Some Primitive layers in European Folk Music. Bulletin of the American Musicological Society 9–10, 11–14. https://doi.org/10.2307/829223
- Hurewitz, J. C. (1961). Ottoman Diplomacy and the European State System. Middle East Journal 15(2), 141–152.
- Huron, D. (1996). The melodic arch in Western folksongs. Computing in Musicology 10(3), 3–23.
- Huron, D. (2001). Tone and Voice: A Derivation of the Rules of Voice-Leading from Perceptual Principles. Music Perception: An Interdisciplinary Journal 19(1),1–64. https://doi.org/10.1525/mp.2001.19.1.1
- Janata, P, Birk, J. L., Horn, J. D. V., Leman, M., Tillmann, B., & Bharucha, J. J. (2002). The cortical topography of tonal structures underlying Western music. Science 298, 2167–2170. https://doi.org/10.1126/science.1076262
- Johnson, T. A. (1994). Minimalism: Aesthetic, Style, or Technique? The Musical Quarterly 78(4), 742–773. https://doi.org/10.1093/mq/78.4.742
- Jones, M. R, & Boltz, M. (1989). Dynamic attending and responses to time. Psychology Revue 96, 459–491. https://doi.org/10.1037/0033-295X.96.3.459
- Jožef-Beg, J, & Mihelač, L. (2019). Na začcetku je bila pesem. / In the beginning there was song. Solški center Novo mesto, Novo mesto, Slovenia.
- Klein, J., & Jacobsen, T. (2014). Music is not a Language. Retrieved from https://www.researchcatalogue.net/ view/114391/114392/0/0.
- Koelsch, S., & Jentschke, S. (2008). Short-term effects of processing musical syntax: An ERP study. Brain Research 1212, 55–62. https://doi.org/10.1016/j.brainres.2007.10.078
- Koelsch, S., & Siebel, W. A. 2005. Towards a neural basis of music perception. Trends in Cognitive Sciences 9, 578–584. https://doi.org/10.1016/j.tics.2005.10.001
- Kostopoulou, E. (2016). Autonomy and Federation within the Ottoman Empire: Introduction to the Special Issue. Journal of Balkan and Near Eastern Studies 18(6), 525–532. https://doi.org/10.1080/19448953.2016.1196039
- Kramer, J. D. (1988). The Time of Music: New Meanings, New Temporalities, New Listening Strategies. Schirmer Books, USA.
- Krumhansl, C. L. (2000). Rhythm and pitch in music cognition. Psychological Bulletin 126, 159–179. https://doi.org/10.1037/0033-2909.126.1.159
- Krumhansl, C. L., & Shepard, R. N. (1979). Quantification of the hierarchy of tonal functions within a diatonic context. Journal of experimental psychology: Human Perception and Performance 5(4), 579–594. https://doi.org/10.1037/0096-1523.5.4.579
- Lappe, C., Steinsträter, O., & Pantev, C. (2013). Rhythmic and melodic deviations in musical sequences recruit different cortical areas for mismatch detection. Frontiers in human neuroscience 7, 260. https://doi.org/10.3389/fnhum.2013.00260
- Lerdahl, F., & Jackendoff, R. (1983). A generative theory of tonal music. MIT Press, Cambridge, MA, USA.
- Levitin, D. J. & Menon, V. (2000). The neural locus of temporal structure and expectancies in music: evidence from functional neuroimaging at 3 Tesla. Music Perception 22, 563––575. https://doi.org/10.1525/mp.2005.22.3.563
- Levitin, D. J., & Tirovolas, A. K. (2009). Current Advances in the Cognitive Neuroscience of Music. Annals of the New York Academy of Sciences 1156 (1), 211–231. https://doi.org/10.1111/j.1749-6632.2009.04417.x
- Ling, J. (1997). A history of European folk music. University of Rochester Press, USA.
- Lu, K, & Vicario, D. S. (2014). Statistical learning of recurring sound patterns encodes auditory objects in songbird forebrain. Proceedings of the National Academy of Sciences 111(40), 14553–14558. https://doi.org/10.1073/pnas.1412109111
- MacKay, D. J. C. (2003). Information Theory, Inference, and Learning Algorithms. Cambridge: Cambridge University Press, UK.
- Marcus, S. (2003). The Eastern Arab system of melodic modes: A case study of Maqam Bayyati. In The Garland Encyclopedia of World Music, 33–44. New York: Routledge, USA.
- Margulis, E. H. (2014). On Repeat: How Music Plays the Mind. New York: Oxford University Press, USA. https://doi.org/10.1093/acprof:oso/9780199990825.001.0001
- Meyer, L. B. (1989). Style and Music. Theory, History, and Ideology. Chicago: The University of Chicago Press, USA.
- Mihelač, L., & Povh, J. (2020a). AI based algorithms for the detection of (ir)regularity in musical structure. AMCS 30(4), 761–772.
- Mihelač, L., & Povh, J. (2020b). The Impact of the Complexity of Harmony on the Acceptability of
- Music. ACM Trans. Appl. Percept. 17(1), 1-27. https://doi.org/10.1145/3375014
- Mihelač, L., Wiggins, A. G., Lavrač, N., & Povh, J. (2018). Entropy and acceptability: information dynamics and music acceptance. In R. Parncutt, & S. Sattmann (Eds.), Proceedings of ICMPC15/ESCOM10.
- Moffat, A. (1990). Implementing the PPM data compression scheme. IEEE Transactions on Communications 38(11), 1917––1921. https://doi.org/10.1109/26.61469
- Nettl, B. (1983). The Study of Ethnomusicology: Twenty-nine Issues and Concepts. University of Illinois Press, USA.
- Nettl, B., & Béhague, G. (1980). Folk and traditional music of the western continents. Englewood Cliffs, N.J., Prentice-Hall, USA.
- Newell, W. W. (1963). Games and Songs of American Children. New York: Dover Publications, Inc., USA.
- Nograšek, M., & Virant Iršič, K. (2005). Piške sem pasla. Ljubljana: DZS, Slovenia.
- Patel, A. D. (2003). Language, music, syntax, and the brain. Nature Neuroscience 6, 674–681. https://doi.org/10.1038/nn1082
- Pearce, M. T., & Wiggins, G. A. (2006a). The information dynamics of melodic boundary detection. In Proceedings of the Ninth International Conference on Music Perception and Cognition, Bologna.
- Pearce, M. T., & Wiggins, G. A. (2004). Improved Methods for Statistical Modelling of Monophonic Music. Journal of New Music Research 33(4), 367–385. https://doi.org/10.1080/0929821052000343840
- Pearce, M. T. (2005). The construction and evaluation of statistical models of melodic structure in music perception and composition. Ph.D. thesis, Department of Computing City University, London, UK.
- Pearce, M. T. (2018). Statistical learning and probabilistic prediction in music cognition: mechanisms of stylistic enculturation. Annals of the New York Academy of Sciences 1423(1): 378–395. https://doi.org/10.1111/nyas.13654
- Pearce, M. T., Conklin, D., & Wiggins, G. A. (2005). Methods for Combining Statistical Models of Music. In U. K. Wiil (Ed.), Computer Music Modelling and Retrieval, (pp. 295–312). Heidelberg, Germany. https://doi.org/10.1007/978-3-540-31807-1_22
- Pearce, M. T., Müllensiefen, D., & Wiggins, G. A. (2010a). Melodic grouping in music information retrieval: New methods and applications. In Advances in music information retrieval, 364–388. Springer. https://doi.org/10.1007/978-3-642-11674-2_16
- Pearce, M. T., Müllensiefen, D., & Wiggins, G. A. (2010b). The role of expectation and probabilistic learning in auditory boundary perception: a model comparison. Perception 39(10), 1365–1389. https://doi.org/10.1068/p6507
- Pearce, M. T., Ruiz, M. H., Kapasi, S., Wiggins, G. A., and Bhattacharya, J. (2010). Unsupervised statistical learning underpins computational, behavioural, and neural manifestations of musical expectation. NeuroImage 50(1), 302–313. https://doi.org/10.1016/j.neuroimage.2009.12.019
- Pearce, M. T., & Wiggins, (2006b). Expectation in Melody: The Influence of Context and Learning. Music Perception 23(5), 377–405. https://doi.org/10.1525/mp.2006.23.5.377
- Pearce, M. T., & Wiggins, G. A. (2012). Auditory Expectation: The Information Dynamics of Music Perception and Cognition. Topics in Cognitive Science 4, 625–652. https://doi.org/10.1111/j.1756-8765.2012.01214.x
- Pole, W. (2014). The Philosophy of Music. Routledge, Taylor & Francis, USA. https://doi.org/10.4324/9781315822730
- Pond, D. (1981). A Composer's Study of Young Children's Innate Musicality. Bulletin of the Council for Research in Music Education 68, 1–12.
- Potter, K., Wiggins, G. A., & Pearce, M. T. (2007). Towards greater objectivity in music theory: Information-dynamic analysis of minimalist music. Musicae Scientiae 11(2), 295–322. https://doi.org/10.1177/102986490701100207
- Prince, J. B., Thompson, W. F., & Schmuckler, M. A. (2009). Pitch and Time, Tonality and Meter: How Do Musical Dimensions Combine? Journal of Experimental Psychology Human Perception & Performance 35(5), 1598–1617. https://doi.org/10.1037/a0016456
- Rohrmeier, M. (2011). Towards a generative syntax of tonal harmony. Journal of Mathematics and Music 5(1), 35–53. https://doi.org/10.1080/17459737.2011.573676
- Rohrmeier, M., & Pearce, M. T. (2018). Musical Syntax I: Theoretical Perspectives. https://doi.org/10.1007/978-3-662-55004-5_25
- Romet, C. (1980). The play rhymes of children: A cross cultural source of natural learning materials for music education. Australian Journal of Music Education 27, 27–31.
- Sauvé, S. A., & Pearce M. T. (2019). Information-theoretic Modeling of Perceived Musical Complexity. Music Perception: An Interdisciplinary Journal 37(2), 165–178. https://doi.org/10.1525/mp.2019.37.2.165
- Schaffrath, H. (1995). The Essen Folksong Collection in the Humdrum Kern Format.
- Schoenberg, A., Strang, G., & Stein, L. (1967). Fundamentals of Musical Composition. London: Faber & Faber London, UK.
- Shannon, C. E., & Weaver, W. (1949). The mathematical theory of communication. Urbana, IL: University of Illionis Press, USA.
- Shannon, C. E. (2001). A mathematical theory of communication. ACM SIGMOBILE Mobile Computing and Communications Review 5(1), 3–55. https://doi.org/10.1145/584091.584093
- Shepard, R. N. (1982). Structural representations of musical pitch. In D. Deutsch (Ed.), The psychology of music (pp. 343–390). Orlando, FL: Academic Press, USA. https://doi.org/10.1016/B978-0-12-213562-0.50015-2
- Steinruecken, C., Ghahramani, Z., & MacKay, D. D. (2015). Improving PPM with Dynamic Parameter Updates. In 2015 Data Compression Conference, 193–202. https://doi.org/10.1109/DCC.2015.77
- Sutton-Smith, B. (1999). What is children's folklore? Utah: USU Press, USA.
- The Meertens Tune Collections. (2019). Dutch Song Database. Retrieved from http://www.liederenbank.nl/mtc.
- Tillmann, B., Bharucha, J. J., & Bigand, E. (2000). Implicit learning of tonality: A self-organizing approach. Psychological Review 107(4), 885–913. https://doi.org/10.1037/0033-295X.107.4.885
- Tillmann, B., & Bigand, E. (1996). Does Formal Musical Structure Affect Perception of Musical Expressiveness? Psychology of Music 24(1), 3–17. https://doi.org/10.1177/0305735696241002
- Trainor, L. J., & Trehub, S. E. (1993). Musical context effects in infants and adults: Key distance. Journal of Experimental Psychology: Human Perception and Performance 19, 615–626. https://doi.org/10.1037/0096-1523.19.3.615
- Trehub, S. E., Bull, D., & Thorpe, L. A. (1984). Infants' Perception of Melodies: The Role of Melodic Contour. Child Development 55(3), 821–830. https://doi.org/10.2307/1130133
- Ulanovsky, N., Las, L., & Nelken, I. (2003). Processing of low-probability sounds by cortical neurons. Nat Neuroscience 6, 391–398. https://doi.org/10.1038/nn1032
- Voglar, M., & Milena Nograšek. (2009). Majhna sem bila. Ljubljana: DZS, Slovenia.
- Volk, A. (2016). Computational Music Structure Analysis: A Computational Enterprise into Time in Music. In M. Müller, A. Chew, & J. P. Bello (Eds.), Computational Music Structure Analysis. Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik, Germany.
- Von Hippel, P. (2000). Redefining Pitch Proximity: Tessitura and Mobility as Constraints on Melodic Intervals. Music Perception: An Interdisciplinary Journal 17(3), 315–327. https://doi.org/10.2307/40285820
- Vuvan, D. T., & Hughes, B. (2019). Musical Style Affects the Strength of Harmonic Expectancy. Music& Science 2. https://doi.org/10.1177/2059204318816066.
- Widmer, G. (2016). Getting Closer to the Essence of Music: The Con Espressione Manifesto. ACM Transactions on Intelligent Systems and Technology 8(2), 1-15. https://doi.org/10.1145/2899004
- Wiggins, G. A. (2010). Cue Abstraction, Paradigmatic Analysis, and Information Dynamics: Towards Music Analysis by Cognitive Model. Musicae Scientiae Special Issue: Understanding musical structure and form: papers in honour of Irène Deliège, 307–322. https://doi.org/10.1177/10298649100140S217
- Wiggins, G. A, Pearce, M. T., & Müllensiefen, D. (2009). Computational modeling of music cognition and musical creativity. In R. T. Dean (Ed.). Oxford handbook of computer music and digital sound culture. Oxford: Oxford University Press, UK.
- Wiggins, G. A., & Sanjekdar, A. (2019). Learning and consolidation as re-representation: revising the meaning of memory. Frontiers in Psychology, 10, 802. https://doi.org/10.3389/fpsyg.2019.00802
- Wu, P., Manjunath, B. S., Newsam, S., & Shin, H. D. (2000). A texture descriptor for browsing and similarity retrieval. Signal Processing: Image Communication 16(1-2), 33–43. https://doi.org/10.1016/S0923-5965(00)00016-3
- Yu, X., Liu, T., & Gao, D. (2015). The Mismatch Negativity: An Indicator of Perception of Regularities in Music. https://doi.org/10.1155/2015/469508


