DESPITE Arnold Schoenberg's (1941/1950) proclamation that "[c]omposition with twelve tones has no other aim than comprehensibility" (p. 103), dodecaphonic (i.e., twelve-tone) music has failed to reach the level of widespread popularity that he and his followers from the Second Viennese School had originally hoped for. As we approach the centennial for the discovery of Schoenberg's "method of composing with twelve tones," discussions about its comprehensibility continue to resurface in academic circles. Music cognition researchers, in particular, have contributed to this debate and sometimes provided important empirical corroboration (see, e.g., Brown, 2016; Dibben, 1994; Dienes & Longuet-Higgins, 2004; de Lannoy, 1972; Krumhansl, Sandell, & Sergeant, 1987; Ockelford & Sergeant, 2013; Pedersen, 1975).

The authors of the current target article, Paul von Hippel and David Huron, made an essential contribution to this endeavor when they presented their initial analysis of anti-tonal (or "contra-tonal") traits in Schoenberg's twelve-tone rows in an unpublished conference paper about 20 years ago (Huron & von Hippel, 2000). Although Huron briefly revisited these results in the penultimate chapter of his Sweet Anticipation (Huron, 2006), the recent paper by von Hippel and Huron (2020) provides the first detailed account in journal publication format and, furthermore, consolidates the original findings by expanding them to Anton Webern's and Alban Berg's rows and by incorporating a set of control variables and a larger control corpus.

A major methodological innovation of this research project is the procedure for quantifying the tonality of twelve-tone rows. Specifically, tonal fit is operationalized as the average of 44 Pearson correlations between the highest-scoring major/minor key profile (see their Figure 2) and sub-segments of cardinality one to eleven—always including the first pitch in the row—of the prime (P), retrograde (R), inversion (I), and retrograde-inversion (RI) forms of each twelve-tone row. In this way, von Hippel and Huron (2020) were able to demonstrate that segments from twelve-tone rows by Arnold Schoenberg (n = 42) and Anton Webern (n = 21) achieved significantly lower tonal fit than segments from randomly generated twelve-tone rows (n = 1,000). There was, on the other hand, no significant difference in tonal fit between the random sample and twelve-tone rows by another famous Schoenberg student, Alban Berg (n = 23), who is known for adhering more closely to tonal traits in his dodecaphonic works (Jarman, 1985). These findings were interpreted to mean that Schoenberg's and Webern's twelve-tone rows are in fact "anti-tonal," i.e. actively composed to avoid tonal features and thus presumably also to circumvent tonal listening schemata.

As it provides a methodologically sound empirical basis for discussions about tonality (and absence thereof) in dodecaphonic composition, von Hippel and Huron's (2020) paper was most certainly worth the long wait. At the same time, their choice of method—which is clearly only one amongst many possible ones—invites for replication using alternative procedures. This may challenge or indeed further substantiate their claims regarding anti-tonality in Schoenberg and Webern (and tonality in Berg for that matter). To that end, below, I offer two methodological expansions of von Hippel and Huron's (2020) analysis. First, I present a close replication of their analysis using a modified operationalization of tonal fit that considers all sub-segments of twelve-tone rows on equal terms rather than having a bias towards initial and final tones of the rows. Second, I quantify the sequential expectancy dynamics of twelve-tone row forms using a computational model of melodic expectation. As will be evident, some of these analyses are consistent with von Hippel and Huron's (2020) findings while others deviate slightly and thus may offer a more nuanced picture of anti-tonal and tonal twelve-tone composition in Schoenberg's, Webern's, and Berg's oeuvres.

CONSIDERING ALL POSSIBLE SUB-SEGMENTS OF ROWS

As mentioned above, von Hippel and Huron's (2020) operationalization of tonal fit averages 44 correlations corresponding to the highest numerical Pearson correlation with any of the 12 major or 12 minor key profiles (cf. Krumhansl & Kessler, 1982) for the 1 to 11 first tones of the P, I, R, and RI forms of each row. Because peripheral (i.e., initial or final) tones of the row are more likely than medial tones to be featured in sub-segments computed in this way, this automatically leads to an imbalance in favor of the former over the latter. This resulting row-initial and row-final bias may indeed be justified in terms of general psychological mechanisms where primacy and recency effects are well-established (Lewandowsky & Murdock, 1989) and in musical practice where themes are often identified by their beginning, as exemplified by dictionaries of musical themes (e.g., Barlow & Morgenstern, 1983). Musical serial order effects also appear, for example, in the reconstruction of order for verses in church hymns (Maylor, 2002). Yet, the current operationalization of tonal fit seems somewhat at odds with dodecaphonic principles of equality between all twelve pitch classes, such as expressed in Josef Matthias Hauer's (1920) "law of the twelve tones" which inspired subsequent dodecaphonic compositional practice. Thus, it seems relevant to test if von Hippel and Huron's (2020) findings hold true with an alternative operationalization of tonal fit that considers all possible sub-segments of the rows.

Results

Figure 1 contains violin plots of the replication of von Hippel and Huron's (2020) results with their original tonal fit measure (left panel) as well as the results from the new analysis with the novel tonal fit measure introduced above (right panel). Unlike the analysis reported by von Hippel and Huron, the measures reported here were not standardized to the mean and standard deviation of random rows but rather occupy the original scale typical of correlation values (i.e., theoretically ranging from -1 to 1 although the selection of the highest correlations makes negative tonal fit values extremely unlikely).

To assess if the twelve-tone rows by the three specific composers differed significantly from random rows, linear regression with robust (i.e., heteroscedasticity-resistant) standard errors was conducted predicting the original and revised tonal fit measures with dummy variables for each of the composers using the lm() function in R (R Core Team, 2018). 3 Similar to the previous study, quantile regression was also conducted to compare the median between the different types of rows. To this end, the rq() function from the quantreg package was used (Koenker, 2020).

As evident from Tables 1 and 2, both types of regression confirmed that Alban Berg's twelve-tone rows did not differ significantly from the random rows neither when tonal fit was calculated as done by von Hippel and Huron (2020) nor when using the revised measure introduced here. The rows by Arnold Schoenberg and Anton Webern, however, showed significantly lower levels of tonal fit than the random rows, and this was the case for both the original and revised measures with both types of regression. Taken together, these follow-up analyses indicate that the effects for anti-tonality in dodecaphonic compositions by Schoenberg and Webern hold true when all row members are considered equally.

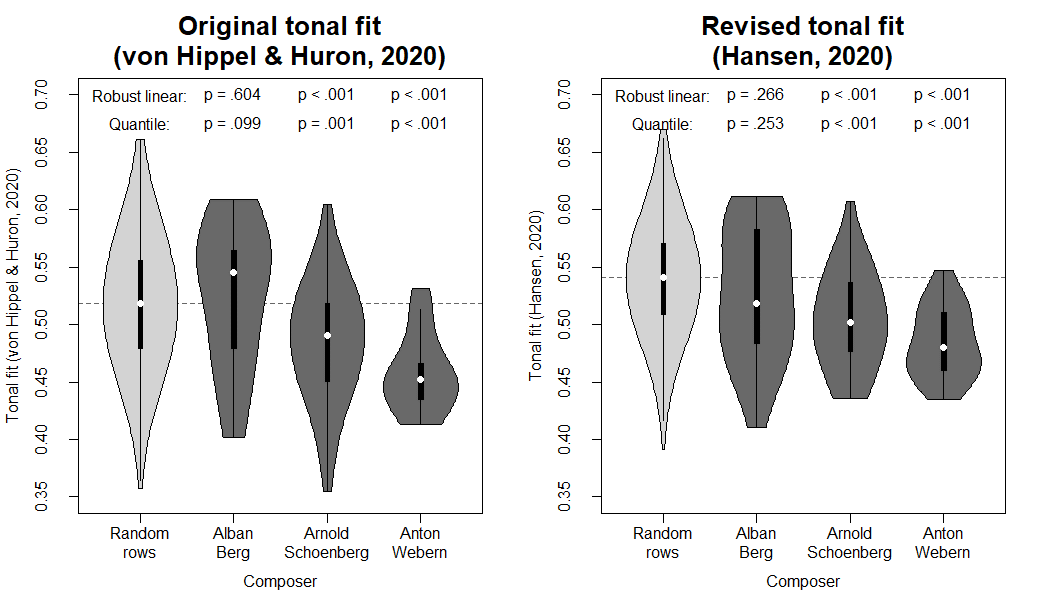
Figure 1. Violin plots of the tonal fit values for the 1,000 random twelve-tone rows as well as the 23, 42, and 21 twelve-tone rows composed by Alban Berg, Arnold Schoenberg, and Anton Webern, respectively. The violins comprise a kernel density plot displayed on top of a conventional boxplot with median (white dot), interquartile range (black box), and lower/upper adjacent values (whiskers). The left panel depicts von Hippel and Huron's (2020) original tonal fit measure whereas the right panel depicts the revised tonal fit measure introduced here which is not biased towards row-initial and row-final sub-segments. As can be seen, the revised measure replicates the original findings that, in comparison with random rows, Schoenberg's and Webern's rows were significantly anti-tonal whereas Berg's rows were not.

Table 1. Linear regression with robust standard errors (left) and quantile median regression (right) of the original tonal fit measure by von Hippel and Huron (2020).

	Linear robust regression			Quantile (median) regression
	Coefficient (SE)	t	p	Coefficient (SE)	t	p
Intercept	0.52 (<0.01)	310.24	<.01	0.52 (<0.01)	220.03	<.01
Berg	0.01 (0.01)	0.52	.60	0.03 (0.02)	1.65	.10
Schoenberg	-0.03 (<0.01)	-4.12	<.01	-0.03 (<0.01)	-3.40	<.01
Webern	-0.06 (<0.01)	-8.09	<.01	-0.07 (<0.01)	-7.63	<.01

Table 2. Linear regression with robust standard errors (left) and quantile median regression (right) of the revised tonal fit measure introduced here.

	Linear robust regression			Quantile (median) regression
	Coefficient (SE)	t	p	Coefficient (SE)	t	p
Intercept	0.54 (<0.01)	384.98	<.01	0.54 (<0.01)	308.13	<.01
Berg	-0.01 (0.01)	-1.11	.27	-0.02 (0.02)	-1.14	.25
Schoenberg	-0.04 (<0.01)	-5.44	<.01	-0.04 (<0.01)	-3.96	<.01
Webern	-0.06 (<0.01)	-8.42	<.01	-0.06 (<0.01)	-6.60	<.01

CONSIDERING SEQUENTIAL EXPECTANCY DYNAMICS IN TONALLY ENCULTURATED LISTENERS

Following in the footsteps of an old discussion in music cognition research regarding whether to operationalize tonality in distributional (e.g., Krumhansl, 1990) or sequential terms (e.g., Butler, 1989), von Hippel and Huron's (2020) method can rightfully be criticized for adhering to the former rather than the latter approach. 4 Neither the original tonal fit measure nor the revised one evaluated above considers the order in which row members occur. Yet, as music unfolds in time, and the human brain engages in "eager processing" whereby incoming sensory input is continually recoded as soon as it arrives (Christiansen & Chater, 2016), perception of musical structure is necessarily sequential rather than retrospectively summative (Hansen, Kragness, Vuust, Trainor, & Pearce, under review).

Specifically in the context of dodecaphonic composition, it has previously been argued that there is a cognitive dimension to understanding the aesthetics and reception of twelve-tone music as well as the historical context in which it emerged. An unbalanced focus on compositional process over perceptual structure—what Taruskin (2004) refers to as "the poietic fallacy"—has undoubtedly not benefitted the popularity of twelve-tone music in the general public. In his discussion of cognitive constraints on compositional systems, Lerdahl (1992) argued that the serial organization of musical sounds as found in many twelve-tone pieces made this music "cognitively opaque" from a listener's perspective. This opaqueness was primarily ascribed to serialism's permutational rather than elaborational melodic structure, its avoidance of sensory consonance and dissonance distinctions, and its inability to induce a pitch space mapping spatial distance to cognitive distance. Along similar lines, other accounts have emphasized how key features of dodecaphonic composition like flat zeroth-order pitch distributions, registral discontinuity (resulting from octave equivalence), limited hierarchical depth of motives, weak metrical scaffolding, rhythmical irregularity, and the lack of well-established cadential formulas and repetitions transgress fundamental principles of music listening (Ball, 2011; Lerdahl, 2001). Humans are, in other words, predisposed for musics that lend themselves well to our cognitive chunking mechanisms, limited working memory capacity, preference for familiar structures, and sophisticated statistical learning and pattern discovery skills.

A growing body of research indeed demonstrates that expectations play a key role in all of these areas. This is, for example, the case for segmentation of music into phrases (Pearce, Müllensiefen, & Wiggins, 2010; Hansen, Kragness, Vuust, Trainor, & Pearce, under review), memory for melodies (Agres, Abdallah, & Pearce, 2018), stylistic enculturation (Hansen, Vuust, & Pearce, 2016; Morrison, Demorest, & Pearce, 2018), and the cognition of musical repetition (Margulis, 2014) and cadence formulas (Sears, Pearce, Caplin, & McAdams, 2018; Sears, Pearce, Spitzer, Caplin, & McAdams, 2019). Thus, claims about anti-tonality in dodecaphonic composition ultimately makes assumptions about psychological expectation mechanisms rather than about musical structure per se (i.e., independent from the listener's perspective). While the key profiles used for computing tonal fit measures above were indeed empirically derived from listening experiments with human participants, they were not used in a way where the order of pitches in the melodic sequence was considered, and they only assessed listener expectations at one particular point in a listening episode. The expectancy dynamics of twelve-tone rows can be modelled more dynamically with computational models of event-based listening such as the one adopted below.

Results

As an initial sanity check, the overall success of each execution of IDyOM (configured as described above) in predicting the random and composed twelve-tone rows was compared with the success of IDyOM executions where the long-term models were trained on the row corpora themselves (via 10-fold cross-validation) rather than on a large, tonal corpus as described above. These alternative models can be viewed as simulating the experience of an expert listener skilled in (only) twelve-tone rows. To this end, model success was quantified in terms of average information content where low values signify that the notes that actually occurred in the sequence were predicted by the model with high probability on average whereas high values, conversely, signify that the model was relatively surprised about the notes in the sequence.

Unsurprisingly, this analysis found that random and composed rows were both predicted more strongly by IDyOM models trained on the rows themselves (mean IC_random: 3.49; mean IC_composed: 3.38) than by IDyOM models trained on the (stylistically somewhat irrelevant) tonal corpus (mean IC_random: 5.82; mean IC_composed: 5.60). The fact that mean IC was lower for composed than for random rows both when predicted by dodecaphonic IDyOM models and by tonal IDyOM models suggests that composed rows contained more systematic combinations of pitch intervals than random rows—both in the context of twelve-tone music and tonal folksongs. While consistent with von Hippel and Huron's (2020) suggestion that Alban Berg may have composed rows with tonal characteristics, these preliminary findings do not overall seem consistent with their conclusions about anti-tonality in Schoenberg's and Webern's music. To assess these issues in greater detail, however, one must proceed to distinguishing between the rows by each of the three twelve-tone composers.

As for the tonal fit measures analyzed above, linear regression with robust standard errors as well as quantile (median) regression were conducted for the two information-theoretic measures IC and entropy (Figure 2 and Tables 3 and 4). This analysis found that to a listener enculturated in tonal music, Alban Berg's and Anton Webern's twelve-tone rows generally contained more expected notes than was the case for the random rows. Arnold Schoenberg's rows, on the other hand, did not show significantly different levels of IC in comparison with the random control corpus. Moreover, while Berg's and Schoenberg's twelve-tone rows were no different from the random rows in terms of mean entropy, Webern's rows were generally estimated to evoke more uncertain pitch expectations in tonal listeners. It will be discussed below how these results differ in interesting ways from von Hippel and Huron's (2020) findings without being incompatible with them.

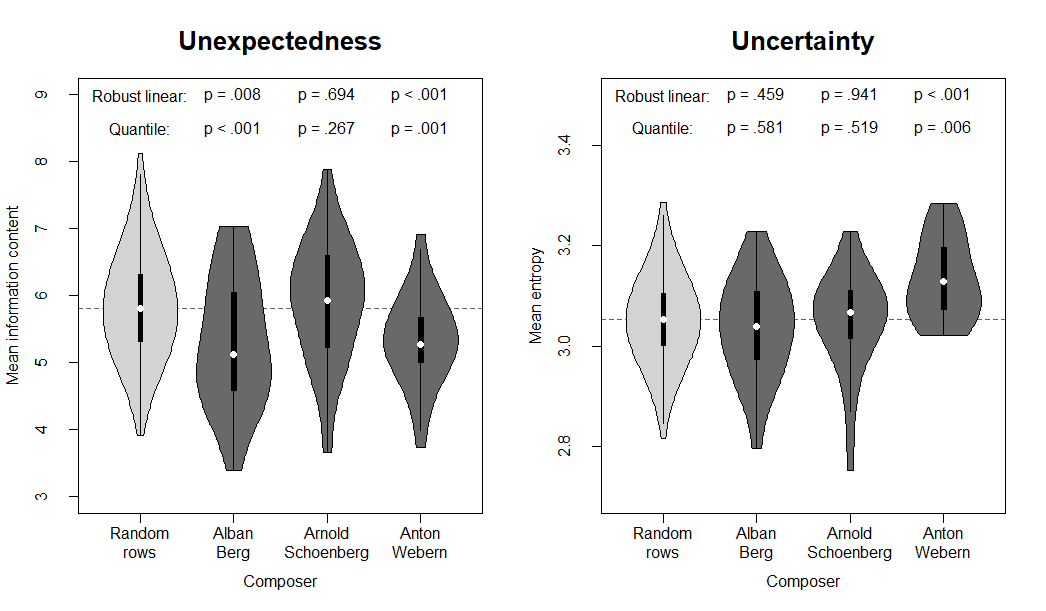
Figure 2. Violin plots of the information-theoretic measures estimated by IDyOM for the 1,000 random twelve-tone rows as well as the 23, 42, and 21 twelve-tone rows composed by Alban Berg, Arnold Schoenberg, and Anton Webern, respectively. The violins comprise a kernel density plot displayed on top of a conventional boxplot with median (white dot), interquartile range (black box), and lower/upper adjacent values (whiskers). The left panel depicts the mean information content which quantifies the average unexpectedness of notes in the row whereas the right panel depicts the mean entropy which quantifies the average uncertainty when listeners make predictions about the next pitch in the row. As can be seen, for listeners accustomed to tonal music, both Alban Berg's and Anton Webern's twelve-tone rows were significantly more expected than random rows whereas Anton Webern's rows simultaneously created more uncertain expectations in listeners. Arnold Schoenberg's rows did, on the other hand, not differ from random rows in terms of these information-theoretic measures.

Table 3. Linear regression with robust standard errors (left) and quantile median regression (right) of the information content measure estimated by IDyOM.

	Linear robust regression			Quantile (median) regression
	Coefficient (SE)	t	p	Coefficient (SE)	t	p
Intercept	5.85 (0.02)	258.11	<.01	5.82 (0.03)	169.95	<.01
Berg	-0.53 (0.20)	-2.64	<.01	-0.69 (0.19)	-3.65	<.01
Schoenberg	0.05 (0.14)	0.39	.69	0.12 (0.11)	1.11	.27
Webern	-0.51 (0.15)	-3.43	<.01	-0.54 (0.17)	-3.19	<.01

Table 4. Linear regression with robust standard errors (left) and quantile median regression (right) of the entropy measure estimated by IDyOM.

	Linear robust regression			Quantile (median) regression
	Coefficient (SE)	t	p	Coefficient (SE)	t	p
Intercept	3.05 (<0.01)	1245.96	<.01	3.05 (<0.01)	1009.75	<.01
Berg	-0.02 (0.02)	-0.74	.46	-0.01 (0.02)	-0.55	.58
Schoenberg	<0.00 (0.02)	-0.08	.94	0.01 (0.02)	0.64	.52
Webern	0.08 (0.02)	4.52	<.01	0.08 (0.03)	2.75	<.01

Additionally, to evaluate the relative contribution of tonal fit, expectancy dynamics, and control variables representing other structural row properties, multiple logistic regression analysis was conducted, following von Hippel and Huron's (2020) procedure of adding all relevant predictors at once (i.e., the "enter" method). All the original control variables were added as predictors, including binary variables for whether rows were (a) inversionally hexachordally combinatorial (IHC), (b) derived from trichords, tetrachords, pentachords, or hexachords, and/or (c) mirror-symmetric, as well as numeric variables for how many (d) semitones and trichords of the (e) (014) and (f) (016) type they contained. In contrast to the target authors' analysis, the revised (unstandardized) tonal fit measure introduced above replaced the original one, and mean information content (IC) and mean entropy were also added to model expectancy dynamics.

The results from the logistic regression analysis complements von Hippel and Huron's findings in a number of interesting ways (Table 5). First, the Schoenberg analysis replicates the findings reported in the original paper and expanded upon here, namely that his rows exhibit significantly lower tonal fit than random, but that mean IC and entropy do not contribute significantly to predicting their status as composed. Moreover, the previously significant tendency for more semitone intervals did no longer meet the significance threshold, thus indicating that some of this variance may have been accounted for by the added (albeit non-significant) information-theoretic predictors. The tendencies for lower entropy and higher chromaticism in Schoenberg's rows both achieved marginally non-significant p-values of .13 and .11, respectively.

Second, similar to what von Hippel and Huron reported, Webern's rows exhibited significantly lower degrees of tonal fit and significantly more semitone intervals and (014) trichords than the random rows. Although entropy was higher and IC was lower in Webern's rows, the related variance could better be explained by these other variables. To explore the patterns of overlapping variance explained, individual logistic regression models were fitted with mean IC and mean entropy in combination with only one of the measures revised tonal fit (AIC = 147.99), (014) trichords (AIC = 152.71), or semitones (AIC = 136.40). Whereas mean IC and entropy remained significant predictors when combined with tonal fit and (014) trichords (all. p's < .03), their contribution became highly non-significant when combined with number of semitones as predictor (both p's > .92). The fact that semitones and the information-theoretic measures explained overlapping variance was additionally supported by the fact that a model with number of semitones as the only predictor achieved lower AIC than any of the other models (AIC = 132.42).

Third and finally, the only significant predictor for Berg's rows was mean IC which was significantly lower than for random rows. The revised tonal fit measure, on the other hand, did not achieve statistical significance. Interestingly, thus, while this could not be established with the distributional tonal fit measures, the lower average surprise evoked by note transitions in the Berg corpus is indeed consistent with the widespread consensus that Berg's twelve-tone rows tend to show tonal characteristics (Headlam, 1996). The fact that mirror symmetry and semitone predictors were no longer significant after the addition of mean IC suggests that low pitch unexpectedness was more predictive of Berg's rows than semitone intervals and symmetrical structure per se.

Table 5. Multiple logistic regression analysis predicting whether rows were random or composed with the revised tonal fit measure, the information-theoretic measures, and the control variables entered as predictors (using the "enter" method), separately for each of the three composers.

	Schoenberg (n = 42)		Webern (n = 21)		Berg (n = 23)
Predictors	Odds ratio [95% CI]	p	Odds ratio [95% CI]	p	Odds ratio [95% CI]	p
Mean IC	1.04 [0.64, 1.71]	.87	0.72 [0.28, 1.90]	.51	0.38 [0.19, 0.78]	<.01**
Mean entropy	0.02 [0, 3.15]	.13	5.93 [0, 57904.05]	.70	0.04 [0, 12.94]	.27
Tonal fit (rev.)	<0.01 [0, 0.02]	<.01**	<0.01 [0, 0.28]	.04*	<0.01 [0, 44.69]	.19
IHC	7.56 [3.05, 18.75]	<.01**	0.90 [0.26, 3.10]	.87	0.84 [0.34, 2.04]	.70
Derived	2.49 [0.39, 15.79]	.33	10.10 [0.88, 115.76]	.06†	3.50 [0.48, 25.58]	.22
Mirror symmetric	3.21 [0.38, 26.81]	.28	1.34 [0.06, 31.23]	.86	7.41 [0.95, 57.91]	.06†
#semitones	1.28 [0.94, 1.74]	.11	2.06 [1.21, 3.50]	<.01**	1.23 [0.81, 1.85]	.33
# (014) trichords	1.89 [1.27, 2.83]	<.01**	3.24 [1.68, 6.26]	<.01**	0.49 [0.21, 1.16]	.11
# (016) trichords	1.33 [0.81, 2.20]	.26	1.02 [0.43, 2.43]	.97	0.92 [0.44, 1.92]	.83
Constant	269078.20	.11	1.28	.99	6935713.99	.08†

IC: Information content; IHC: inversionally hexachordally combinatorial; p-values result from Wald tests; **p < .01, *p < .05, †p < .10

CONCLUSIONS

Motivated by the theoretical importance of equality between all pitch classes in twelve-tone music and by a long-standing debate in music cognition research between distributional and more dynamic tonality concepts, this commentary provides two methodological expansions of von Hippel and Huron's (2020) empirical report on tonality and anti-tonality in twelve-tone rows by Arnold Schoenberg, Anton Webern, and Alban Berg.

First, a full replication with a novel tonal fit measure without the original bias towards row-initial and row-final sub-segments was presented. The only small deviations from findings with the original measure was that the median revised tonal fit for Alban Berg was no longer numerically higher than that for random rows, and that the original non-significant tendency towards higher-than-random tonal fit for Berg when conducting quantile regression was also no longer present. This suggests that Berg's twelve-tone rows are not truly more tonal than random rows when tonality is assessed in distributional terms. Alternatively, tonal traits could be more prominent at the beginning (or end) of the rows, but this speculation would require more detailed testing to be properly established.

Second, the unsupervised, variable-order n-gram model IDyOM was trained on a large corpus of tonal folksongs to emulate the expectations of Western-enculturated listeners. Before interpreting the results from these simulations, however, an important methodological caveat remains: the unsurprising finding that the tonally-trained model performed worse than a model trained on the twelve-tone rows themselves raises the question whether listeners truly resort to tonal listening schemata when listening to twelve-tone music. Previous evidence already suggests that listeners may not always revert to a stylistically inappropriate schema even though it would result in stronger predictions than a more stylistically appropriate schema that they have limited training in. Hansen, Vuust, and Pearce (2016), specifically, found that professional classical musicians and non-musicians did not seem to misapply general tonal expectations when listening to bebop solos by Charlie Parker. This finding can be explained in terms of "cognitive firewalls" which restrict the use of internalized probabilistic knowledge by contextual relevance (Cosmides & Tooby, 2000; Huron, 2006). Future research uncovering the specifics of schematic listening behavior for dodecaphonic music may provide important context for the interpretation of the findings presented here.

Keeping the aforementioned methodological caveat in mind, statistical analysis of the IDyOM estimates did indeed seem to provide empirical evidence for von Hippel and Huron's (2020) assertion of "tonally evocative rows" (p. 110) in Alban Berg's dodecaphonic works. Berg's rows contained pitches that were on average more expected than pitches in the corpus of random rows. At the same time, the expectations evoked by Berg's rows were neither more nor less uncertain than those evoked by random rows. Logistic regression with structural control variables, furthermore, confirmed that the higher degrees of expectedness explained variance more effectively than structural factors. This variance was previously accounted for by predictors representing the prominence of semitones and mirror symmetry properties.

Interestingly, Webern's rows generated significantly more uncertain expectations in listeners, but resolved such high degrees of uncertainty with relatively highly expected pitch transitions on average. Because semitone intervals are extremely common in tonal music, this would be consistent with von Hippel and Huron's (2020) finding that Webern's well-known predilection for the semitone interval (Hanson, 1983) extended into his dodecaphonic period. The multiple logistic regression analysis demonstrated very clearly that the number of semitone intervals present in Webern's rows explains nearly the exact same variance as that explained by the combination of high uncertainty and low unexpectedness. Tonal fit, conversely, did explain unique variance not accounted for by the semitone predictor. Thus, it seems that Webern composed twelve-tone rows with relatively many semitone intervals which—as is the case for the leading-tone-to-tonic resolutions in tonal music—are both highly expected and lead to relatively uncertain expectations about what follows next (Huron, 2006). Butler's (1989) characterization of semitones as rare intervals carrying "critical information about local harmonic goals" (p. 233), in other words, manifests in Webern's dodecaphonic pieces in terms of row segments that score high on the distributional tonal fit measures.

Finally, whereas Schoenberg's rows achieved lower distributional tonal fit values and had a greater prominence of (014) trichords and inversional hexachordal combinatoriality than random rows, they did not seem to capitalize on different levels of entropy and information content. Thus, the information-theoretic analysis overall failed to generalize von Hippel and Huron's findings of distributional anti-tonality in Schoenberg's music to the ongoing expectancy dynamics of tonally-enculturated listeners. This inconsistency perfectly exemplifies how distributional and sequential/dynamic measures are capturing different aspects of tonality that are not necessarily mutually dependent and overlapping.

In his recent review of the long-standing debate about the distributional vs. sequential nature of musical tonality, Schmuckler (2016) concluded that "distributional and structural-functional approaches are really part of the same process, and that a complete description of tonality and key-finding will require both global distributional properties, along with more localized, structural-functional information" (p. 148). The two methodological expansions of von Hippel and Huron's (2020) study offered here contribute fruitfully to both of these analytical perspectives.