CONTEMPORARY computational music theory has been partially – if not mostly – built on analogies between statistical learning and corpus statistics. 2 The logic generally runs something like this: if learners internalize expectations of a musical style by being exposed to music in that style, then we can study those expectations by identifying trends, norms, and probabilities within a corpus that approximates a listener's exposure. The classic citation for this idea is David Huron's Sweet Anticipation (2006), but the idea goes back to the early work of Carol Krumhansl, who – while relying on years of prior research (Zajonc, 1968) – articulated this argument in music research even before the psychologists and cognitive researchers who would bring the concept of statistical learning to a broader audience (Krumhansl & Kessler, 1982; Krumhansl, 1990; Saffran et al., 1996).
However, in this reciprocity between learning and corpus analysis, there exists a somewhat fuzzy relationship with pedagogical materials. Specifically, there can be a temptation in corpus analyses to equate "used in the music-theory classroom" with "representative of a style" and "approximating a listener's experience." Compare, for instance, the number of times the complete Johann S. Bach chorales have been used in corpus analyses with the number of people whose listening experience is (and has ever been) best approximated by the contents of the Riemenschneider complete harmonized collection. We teach the Bach chorales. We don't listen to the Bach chorales.
To be clear: there are plenty of reasons to rely on pedagogical or pedagogically-influenced corpora. After all, what we teach/are taught informs what we listen to, and what we listen to informs what we teach. Additionally, building a truly representative sample of an entire musical tradition is a tall task (London, 2013), and relying on the inherited expertise of textbooks and curricula seems like a reasonable solution to this problem. Finally, studying a corpus of pedagogical materials on a topic can provide an academic discourse with a measure of introspection, showing the values and priorities that teachers bring into the classroom when teaching that topic (Baker, 2019), as well as distinctions between the explicit knowledge learned in the music theory classroom and the implicit knowledge gained by exposure (Kim, 2011).
Nevertheless, we need to be aware of the ramifications of using pedagogical corpora as stand-ins for broader compositional practices. The motivations behind compiling a syllabus of musical examples can differ from the motivations behind compiling a representative corpus. In the classroom, for instance, we spend more time on difficult concepts, highlight our own favorite pieces, and seek out short examples that efficiently and densely present the concepts listed in our syllabi. We choose pedagogical examples for pedagogical reasons. Therefore, using pedagogical corpora as if they are representative of some larger style can end up over- and under-representing aspects of the actual compositional practice of that repertoire.
This essay shows a few examples of the differences between pedagogical corpora and repertoire-based corpora. The former include datasets derived from textbooks or other classroom materials, while the latter are datasets compiled around a composer's output, the consumption or performance practices of a group of people, or a large sample of a musical genre. I demonstrate these differences in two case studies, first focusing on melodic chromaticism and key profiles (i.e., the relative frequencies of scale degrees expected when music expresses a key), and secondly on chromatic harmony. In both studies, I will make some general observations, followed by a focus on one particular metonym of these larger categories: the melodic sequence of scale degrees ^5–#4 in the former case, and the augmented sixth chord in the latter. My goal is in no way to be exhaustive within this essay. Surely, there are plenty of domains not addressed in this paper in which pedagogical and repertoire-based corpora are similar and different. Rather, I hope to argue for a degree of caution when using pedagogical materials to study the tendencies of musical styles and practices, while also suggesting some ways that pedagogical corpora can yield particular insights into musical traditions and the way we teach tonality in our classrooms.
CHROMATICISM IN MELODIES AND IN SCALE-DEGREE DISTRIBUTIONS
Relative Frequencies of Diatonic and Chromatic Scale Degrees
Figure 1 represents the first 410 major-mode exercises in a corpus of melodies used in Berkowitz et al. (2011)'s ear training textbook, A New Approach to Sight Singing, or what Baker refers to as the MeloSol corpus. 3 The figure orders the examples as they are in the textbook. Here, the proportions with which the tonic triad's scale degrees appear, along with the proportions of other diatonic scale degrees and of chromatic scale degrees are each shown with white, grey, and black boxes, respectively. 4 Each series of 10 exercises is grouped together to show these proportions (i.e., the first most-leftward column represents the first ten exercises in the corpus, the next column represents the next ten, and so on). As the book progresses from that point, the density of chromatic exercises becomes sequentially thicker. At the beginning of the sequence, the tonic triad and other diatonic tones occur exclusively; the pieces then become increasingly more chromatic. By the end, the tonic-triad, diatonic, and chromatic tones all share roughly the same proportion of the distribution.
Fig. 1. The proportion of Tonic, Diatonic, and Chromatic scale degrees in each group of 10 major-mode examples from the MeloSol corpus.
Importantly, there is no ambiguity about this dataset's origin or purpose: this corpus constitutes melodies used in the ear training classroom. It illustrates how we impart notions of normative melodic motion; how we teach students to identify the key orientation of these melodic motions; how we train students to hear the preparations and resolutions of dissonances; and how we instruct students to incorporate chromaticism into a melody, all the while showing the sequence in which we teach these concepts. Figure 1 shows an aspect of how this textbook teaches these topics: the book encourages students to hear chromaticism as an elaboration of some underlying diatonic background. Students first become familiar with the diatonic system before chromatic tones are slowly added to that baseline foundation.
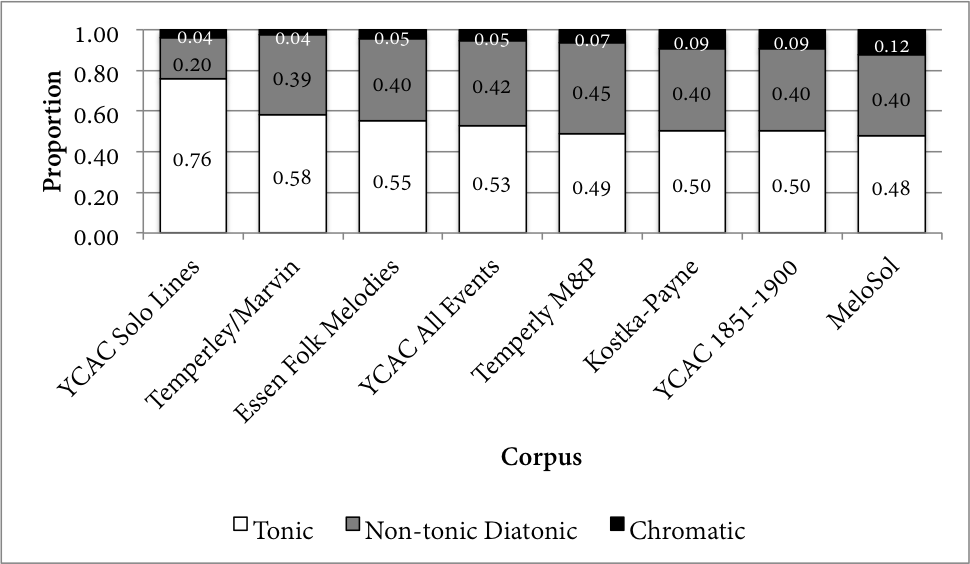
However, because the last quarter-or-so of the examples feature such heavy chromaticism, the book is, on aggregate average, notably more chromatic than other tonal corpora. Figure 2 represents the same information as Figure 1, but now using the distribution of scale degrees within the entirety of several corpora. Each distribution shows the relative frequency of each category of scale degree. For scale-degree counts, I use frequency of occurrence rather than duration throughout this essay. The three least chromatic corpora are the Yale-Classical Archives Solo Lines (counts of successions of singletons within the YCAC; White & Quinn, 2016), the corpus of Haydn and Mozart string quartet openings reported in Temperley & Marvin (2008), and the Essen Folk Melody corpus (Schaffrath, 1995; as accessed on the music21 platform; Cuthbert & Ariza, 2010). This is followed by all events in the YCAC, and the values reported in the key profile introduced in Temperley's (2007) Music And Probability. 5 Next, I show the Kostka-Payne corpus (derived from the key profile calculated from examples in its eponymous textbook; Temperley, 2009), and the MeloSol corpus. I also isolate the most chromatic 50-year portion of the YCAC's data, 1851-1900, for comparison. That is, this chronological portion of the YCAC All Events corpus is tested on its own for illustrative purposes; I return to its significance below.
Notably, the least chromatic corpora – the YCAC, Temperley/Marvin, and Essen corpora – are not constructed around pedagogical logic (the YCAC, for instance, contains files created by the users of classicalarchives.com, while the Temperley/Marvin corpus is simply derived from the output of certain composers in a certain genre) while those explicitly drawn from textbooks are among the most chromatic. In other words, the pedagogical corpora are more chromatic than the repertoire-based corpora. Furthermore, the balance of the textbook's chromaticism aligns more with that of melodies from the later-19th-century portion of the YCAC, suggesting that the ear training curriculum represented by the MeloSol corpus may have a particular historical window with which its exercises may be more aligned. There is more to be said about the potential privilege given to chromatic music and/or 19th century music when we teach European "tonal" music, but this short essay is not the place to do engage in such discussions. Overall, corpora that are compiled around some sort of general performance, composer-based, or listening practice are less chromatic than those centered around pedagogical practice, at least in this small sample.
Behaviors of Selected Chromatic Scale Degrees
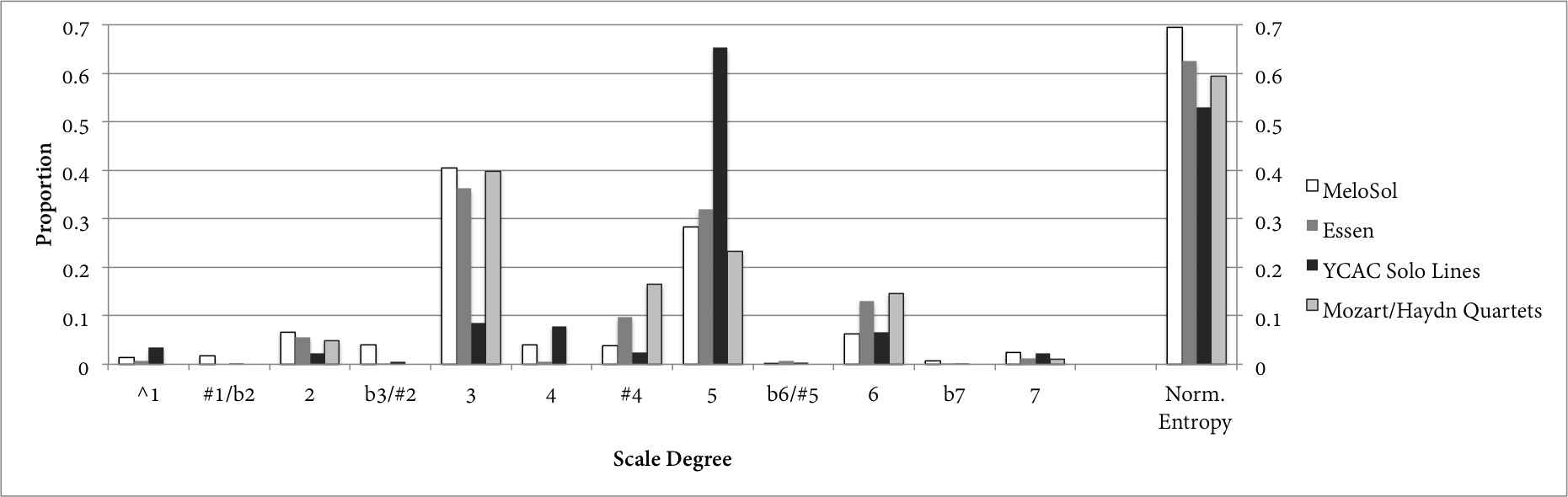
The MeloSol's chromaticism behaves in roughly the same way as other corpora, including non-pedagogical corpora. Figures 3 and 4 show examples of this. The former isolates those instances in which a melody moves to the chromatic lower neighbor of a diatonic scale degree, and determines what interval follows that event, with intervals tabulated modulo 12 (such that a minor third ascent and major sixth descent both register as a move of 3 half steps from the point of origin). "Chromatic lower neighbors" were defined as successions moving downward by half step – an interval of negative 1, or, 11 (mod 12) – between a diatonic scale degree and a subsequent chromatic scale degree. In both Figures 3 and 4, only major-mode examples were used. The latter shows what scale degree follows the sequence <^5→#4>. The corpora now consist of the MeloSol, Essen, and YCAC's solo-line datasets, as well as the individual parts for each instrument in the Mozart and Haydn string quartets found in the music21 corpus. In both instances, the contours of the distributions are roughly the same: each corpus tends to treat these instances of chromaticism in broadly the same manner. In the case of the chromatic half step data, each corpus's vector correlates to one another quite well, with correlation coefficients registering higher than .91.
The ^5-#4 data are somewhat more complicated: with the exception of correlations involving the YCAC, coefficients are all higher than .95. However, that corpus's solo lines move far more to ^5 than ^3, the latter of which is more frequent in other corpora, a difference that yields much more middling correlations (between .45 and .66). 6
Fig. 3. Interval (mod 12) following a descending half step that progresses from a diatonic to a chromatic scale degree (i.e.: what interval follows a descending chromatic half step?).
However similar, the MeloSol melodies do feature relatively more peripheral events than the other corpora. Comparatively, more of its probability mass is taken up by lower-probability events. To quantify this, Figures 3 and 4 also include normalized Shannon entropy values for each distribution: values which run from 0 (when a probability distribution has one entirely certain outcome) to 1 (when a distribution's outcomes are all equally likely). 7 Equation 1 shows the formula for normalized entropy as the proportion between the sequence's entropy (the level of certainty/ constraint of a distribution) and its maximum possible entropy (or, what the entropy would be in a uniform distribution; Margulis & Beatty, 2008). In both figures, the MeloSol entropy outpaces the other corpora, indicating that its chromatic progressions are less predictable and constrained than those of other corpora. Just as the pedagogical corpora contain more overall chromaticism than repertoire-based corpora, this ear-training textbook features proportionately more complexity than exists in other corpora.
Equation 1: ηx= =
CHROMATIC HARMONY
Relative Frequency of Chromatic Chord Roots
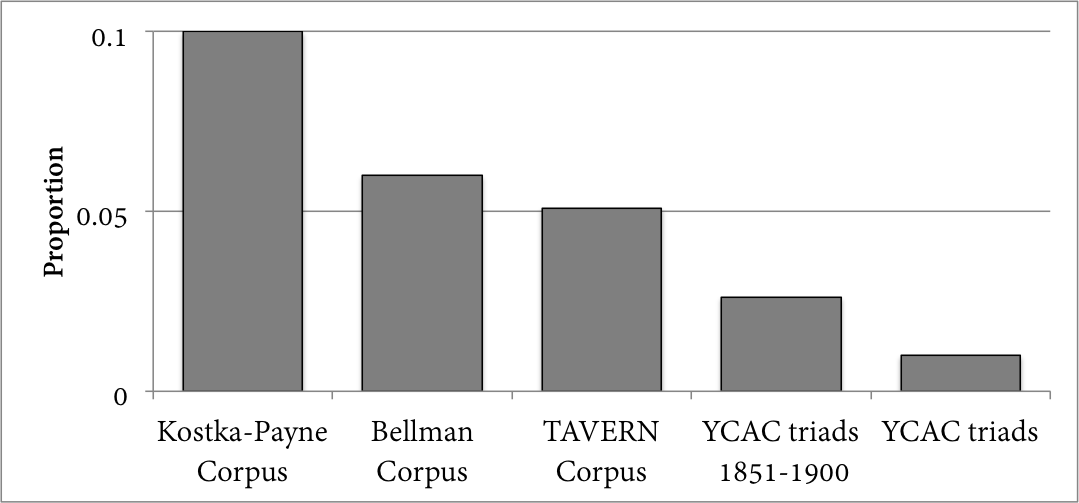
Comparing harmonic annotations of various corpora is considerably less straightforward than counting scale degrees. Assigning a "chord" involves some type of analysis and requires a series of assumptions about how to parse a musical surface, choices about the vocabulary of chords being used, and what sorts of annotations are assigned to these chords (White, 2018). 8 However, with these caveats in mind, corpus analyses of harmony can also show some notable differences between the distributions and behavior of chords within pedagogical and non-pedagogical corpora. Figure 5 shows the proportion of chords rooted on chromatic scale degrees in four harmonic corpora, using only the datasets' major-mode portions. The Kostka-Payne corpus features the most chromatic roots, followed by the Bellman (2005) corpus, a corpus based on hand-made harmonic analyses of excerpts of music from 24 Western European composers from the 18th and 19th centuries. Following theses, the figure shows the proportion of chromaticism in the TAVERN corpus (Devaney et al., 2015): a corpus of hand-made Roman-numeral analyses of themes and variations by Beethoven and Mozart. The analyses in this corpus use multiple annotators, but for this study, I used only "Annotator A." Finally, the YCAC triads (a tally of the roots of all triads that appear in the YCAC) sport the smallest proportion of chords rooted on chromatic degrees. 9 Again for comparison, I also isolated the most chromatic half-century portion of the YCAC, 1851-1900, and have shown the proportion of chromatic roots in that sub-corpus. 10
Similar to the above models of melodic chromaticism, these representations of chromatic harmony show that the explicitly pedagogical corpus – the Kostka-Payne – contains more chromatic events than those associated with corpora drawn from wider swaths of musical practices. 11 And again, we find that chromaticism is represented higher in the late 19th century in the YCAC than in the YCAC as a whole. With the caveat that each of these corpora approach the concept of "chord" in different ways, these numbers do seem to lend further support to the observation that pedagogical corpora represent more chromaticism in aggregate, and in so doing they potentially align more with the particular practice of late romanticism.
Usage of the Augmented Sixth Chord
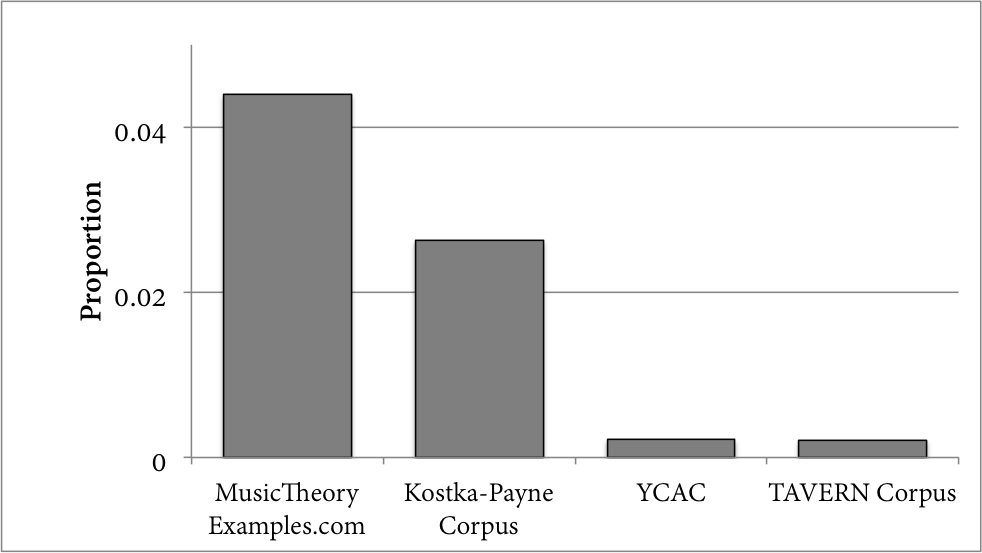
Figures 6 and 7 make a similar study of a particular type of chromatic chord: the augmented sixth. This chord contains a lowered ^6 in the bass voice, and a raised ^4 in another voice (thus creating the interval of an augmented sixth) and is the perennial subject of at least a chapter in standard music theory textbooks (for example, Aldwell & Schachter, 2003; Laitz, 2012). Figure 6 shows the number of augmented sixths within each corpus as a proportion of all events in the corpus. To include another explicitly pedagogical data point, this figure uses the musical excerpts from MusicTheoryExamples.com along with those from the Kostka-Payne corpus, YCAC, and TAVERN corpora. 12 Once again, the two pedagogically-oriented corpora contain relatively more examples of this particular sonority compared to the other two corpora. Figure 7 further divides the YCAC's proportion into half-centuries. As we have seen numerous times, this chromatic event has its greatest representation in the last half of the 19th century: indeed, the chord appears to have a steady increase from the early 18th century towards its peak usage. Similar to the pedagogical corpora's emphases on melodic chromaticism, these corpora's usage of the augmented sixth chord potentially reflects the practice of a particular portion of the Western European tonal tradition more than the wider tradition as a whole.
To further investigate whether the behaviors of these chords are different in pedagogical versus non-pedagogical corpora, I calculated probabilities for all events that followed augmented sixth chords in these corpora, limiting the calculations to the German version of this chord, as it was the most frequent type (by far) in each corpus. A simple bigram approach was used, with the probability of a continuation being the ratio of the count that a chord follows a German augmented sixth, divided by the count of German augmented sixths. The complexity of these probability distributions was again quantified by their normalized Shannon entropy, just as was done in Figure 3. Five corpora were used: the Kostka-Payne corpus, the examples posted on MusicTheoryExamples.com, the YCAC, and the TAVERN corpus; to add another pedagogical dataset for comparison, examples from the Aldwell-Schachter textbook's "Augmented Sixth Chords" chapter were also analyzed. 13 The resulting values are shown in Figure 8. 14
Fig. 8. Normalized entropy for the distributions of chords following German augmented sixth chords, using bigram probabilities.
Paralleling the above melodic data, the distributions derived from pedagogically oriented corpora have higher entropies than other corpora: less-frequent resolutions occupy more of the Kostka-Payne and Aldwell-Schachter probability distributions than the repertoire-based corpora's distributions. Indeed: all corpora agree that the chord moves most frequently to dominant harmonies (be they the cadential "I64" or root-position dominant harmonies). However, while the repertoire-based corpora see dozens of standard resolutions for every non-standard resolution, the textbooks have a higher ratio of non-standard resolutions. Similar to the relative amount of chromaticism within these corpora, there are proportionately more low-probability events in pedagogical corpora than repertoire-based corpora.
PEDAGOGY AS ONE OF TONALITY'S MANY MANIFESTATIONS
These two case studies illustrate some ways that pedagogical and repertoire-based corpora can have differing statistical properties. These studies particularly highlight that pedagogical corpora feature: a) relatively more chromatic events than repertoire-based corpora; b) less constrained usages of these events relative to repertoire-based corpora; and c) some distributional properties that suggest a greater similarity to the later 19th century than to other portions of tonal repertoires.
Of course, there are good reasons for this! It is not a textbook's job to distribute its examples in a way that strictly aligns with compositional practice. Rather, a textbook's job is to present, describe, and catalogue the musical norms, and then present exceptions and outliers, with its accompanying text adding context to its examples. Any harmony textbook will follow a series of examples that illustrate some standard practice (e.g., a normative resolution of a harmony) with examples that illustrate non-standard practices (e.g., some unusual resolutions of that harmony). Due to the fewer overall examples, these corpora will have very different ratios between the frequent and less-frequent resolutions. These materials have the luxury of accompanying texts: a textbook can simply say that a given resolution happens most often instead of manifesting that resolution proportionate most often in its examples. Furthermore, more complex concepts require proportionally more focus in a pedagogical format, with the amount of time devoted to a subject being a function of its difficulty rather than its frequency within a repertoire. In other words, the specific motivations and goals behind a pedagogical text will create observable differences between a corpus based on that text and the repertoire about which that text is teaching.
Because of these differences, the statistics one derives from a pedagogical corpus have the potential to model tonal events differently to other types of corpora. I began this essay by discussing the frequent equation between corpus models and statistical learning, describing corpus-based models as approximating the cognitive models of listeners who have been exposed to those corpora. This study suggests that a model based on a pedagogical corpus would differ from a model based on a larger repertoire. In sum, different models of tonal cognition would arise depending on whether a researcher derives their models from a pedagogical corpus or from a repertoire-based corpus.
Furthermore, because pedagogical corpora are motivated to illustrate unusual events and resolutions with a relatively high frequency, the resulting aggregate statistics of a textbook have the potential to align with the most adventurous portion or portions of that textbook's repertoire. This essay showed several pedagogical corpora emphasizing chromaticism to such an extent that they aligned more with the practices of the later 19th century than with those of broader tonal repertoires. Therefore, if a corpus study uses the examples from a textbook that purports to teach, say, Western European tonal harmony from 1650-1900, the resulting pedagogical corpus will approximate the most experimental portion of that repertoire rather than the broader subject of the textbook. 15
On the one hand, these observations might suggest that pedagogical corpora should be discarded as illegitimate bases for cognitive modeling. Corpus analyses' connections to cognitive modeling rely on the concept of implicit learning, and – by definition – pedagogical texts exist within the domain of explicit learning. As this essay demonstrates, the different tactics and motivations that accompany explicit learning can lead to substantial differences between a textbook's contents and the music to which a listener might be exposed. From this standpoint, a pedagogical corpus is only useful in understanding how we explicitly teach concepts and is not a useful way to study implicit knowledge of these concepts.
Nevertheless, I would argue that corpus analysts should embrace the unique perspective provided by pedagogical corpora. "Tonality" is a semifluid concept that solidifies around times, places, approaches, and definitions. Elsewhere, I have demonstrated that the properties of tonal corpora change sufficiently between time periods such that key-finding models trained on chronologically distinct corpora can assess different keys within the same passage (White, 2014, drawing on Byros, 2009). A similar effect arises when one compares chord-based key-finding models with those oriented around pitch-class distributions (Quinn, 2010; White, 2018); and even the relative frequencies of scale degrees significantly change at different absolute pitch levels (Quinn & White, 2017). Given the variation I have outlined in this short essay, I would argue that it can be useful to consider "pedagogical tonality" as a unique manifestation of tonality, at least insomuch as pedagogical corpora produce markedly different aggregate tonal statistics. The musical examples we use in our classrooms capture a way that musicians think about and practice music, and an aggregate statistical model of these examples captures that way of thinking about and practicing music. After all, many listeners are exposed to particular repertoires only from classroom experiences, and a pedagogical model would describe this kind of listener's understanding of that repertoire. Embracing pedagogical tonality will help us not only better understand how tonality exists within the classroom but will free analysts to further study differences between the various and multifaceted ways that tonal traditions can manifest at different times, places, and modes of presentation.
The choices we make when creating pedagogical tonalities are not trivial. As music theory struggles with how to negotiate the connections between its inherited musical "canon" and white supremacy (Ewell, 2020), it is becoming increasingly important to not only critically engage with the notion of "art music," but to study how our construction of that concept has been expressed, re-imagined, and perpetuated in the classroom. If we carve out epistemological space for pedagogical tonality as distinct from compositional or performance practice, we can better interrogate what and how we teach.
ACKNOWLEDGMENTS
This article was copyedited by Lottie Anstee and layout edited by Diana Kayser.
NOTES
-
Correspondence can be addressed to: Christopher White, UMass Amherst Music Department, 151 Presidents Dr, Amherst, MA 01003; cwmwhite@umass.edu.
Return to Text -
In fact, I am unaware of anyone currently working in this subdiscipline who has not at least implicitly dipped their toe in the waters of statistical learning. On the surface, people working on the properties of historical corpora might seem to be exempt from such a sweeping proclamation. However, that literature often evokes ideas of historically situated cognition (Byros, 2009) in which an analysis tries to uncover how music might have been thought about or heard by its original (or otherwise non-current) audiences.
Return to Text -
This corpus is introduced in Baker (2019; under review). There were several encoding errors in the key annotations, usually confusing E-flat major with E minor (including the examples #38, #41, #72, #207). I manually altered these in my analyses, but I freely admit that I may have missed some errors.
Return to Text -
This doesn't include the "literature" section of the corpus and excludes the last two-dozen-odd examples, which seem to be mostly modal and not chromatic, and therefore do not participate in the trend I'm outlining.
Return to Text -
For the Music and Probability proportions, I used the key profile that Temperley finds to have a maximum key-finding success using his Bayesian method. The corpus is based on a selection of tonal pieces selected by the author for their straightforward expression of key. To my eye, this corpus is something of a middle-ground between corpora that are constructed around music consumption practices and pedagogical practices. I would argue that corpora that aim for a generic sample of a style are still influenced by music theory pedagogy, because the pieces that an analyst has on hand are likely also those pieces they teach. Such corpora are therefore (albeit, arguably) as much motivated by and representative of classroom teaching as they are snapshots of concert repertoires or playlist constituencies.
Return to Text -
The vectors are all significantly different (p>.001) according to χ2 tests, likely a fallout of the large sample size. It also should be noted that the differences observed in the YCAC could be due to the key-finding process used to assign scale degrees. As described in White and Quinn (2016), the corpus's "local scale degrees" are assigned by a windowed key-profile analysis, specifically using the Bellmann-Budge vector as implemented in music21.
Return to Text -
The value for normalized entropy ηx is the proportion of a distribution's entropy divided by its maximum entropy, with entropy being the sum of the logarithm of all probabilities within a distribution, weighted by their probability of occurrence. The maximum entropy is the logarithm of the number of possible outcomes. Strictly speaking, because entropy calculations are not designed to deal with probabilities of 0% (i.e., impossible outcomes), normalized entropy will approach zero, but will never reach zero.
Return to Text -
The YCAC, for instance, simply labels its events as scale-degree sets, using key orientations assigned by a key profile analysis (White and Quinn 2016); Bellmann (2005) is using chord distributions to create a key profile vector for tonal analysis; while the Kostka-Payne corpus of Temperley (2009) uses the Roman numerals given in the textbook's instructors' manual.
Return to Text -
I isolated only triads, because it would not be obvious how to calculate the "roots" of many of the non-traditional surface-level chords in the YCAC (e.g., passing and neighboring dissonances). I therefore queried the YCAC simply for triads (set classes [047], [037], and [036]) and used the zero-th members of those sets as the roots.
Return to Text -
Again, this broad comparison is designed to contrast the properties of corpora, even though they use different definitions of "chord." While Temperley (2009) explicitly reports the roots of chords, the YCAC counts used here contain only a portion of that larger corpus. Likewise, Bellmann (2005) does not report the full list of chords; however, given that the reported scale-degree distribution was taken from the full list, I am assuming the distribution is a reasonable approximation of chromatic roots (if anything, my approach over-represents these chromatic tones). Finally, while the TAVERN corpus reports Roman numerals, I isolated those annotations that indicate non-diatonic roots by hand. However different these representations may be, the proportions do capture a recurrent property between these corpora: the ratio between the items a corpus represents as chromatic and the size of that corpus. Throughout, only major mode portions were used, given that it is not obvious whether the leading tone and subtonic (and even the Neapolitan) degrees are "chromatic" or fundamental degrees of that scale.
Return to Text -
The Bellmann corpus represents an interesting middle-ground between the pedagogical and ecological, somewhat akin to the Music and Probability corpus discussed above. This corpus consists of the hand analyses of selected musical excerpts done in 1937 by Helen Budge for her PhD thesis at the Columbia Teacher's College; we can imagine that she selected pieces that were at hand, and likely strongly represented pieces she used in the classroom.
Return to Text -
For the MusicTheoryExamples.com proportion, I used the number of examples associated with "Chapter 25: Augmented Sixth Chords" as reported on their homepage, and divided that by the total counts of all examples from all topics/chapters reported on their homepage. For the YCAC, the proportion is calculated as the ratio between: a) all events with both mod-12 scale degrees 6 and 8, with 3 or more members in the chord, and with scale-degree 8 (mod 12) in the bass; and b) all events. The Kostka-Payne and TAVERN proportion used counts of chord-type annotations that indicated an augmented sixth. For the Kostka-Payne corpus, I am not using the files available in/linked from Temperley (2009), but rather am using source files generously provided to me by the author which include the events' chord types, which involve explicit annotations of augmented sixths.
Return to Text -
For the Kostka-Payne corpus, I counted all "Ger6" annotations (again, using the source files described in a previous footnote). Similarly, hand annotations of "Gr6," "Gr65," and the like were used in the TAVERN tally. The YCAC counts isolated the scale degree set [8, 0, 3, 6] with [8] in the bass (discounting events that occur only a single time (a technique used when examining large corpora whose probability distributions feature long, low-probability tails: Quinn & Mavromatis, 2011). The Aldwell & Schachter and MusicTheoryExamples.com examples used hand counts that tallied instances of German augmented sixths with lowered scale-degree 6 in the bass (i.e., not in inversion) and were clearly in a single key (i.e., instances reinterpreting the chord as V7/bII were not used). Hand counts were done by myself and Emily Schwitzgebel (a music theory graduate student). Given that these are hand counts, I freely admit that there can be inaccuracies or choices that might be made differently by different analysts; however, the trends would most likely remain even with the addition or removal of a few examples.
Return to Text -
Importantly, normalized entropy allows for the comparison of sequences with different numbers of possible outcomes. While models of scale-degree resolutions all involve 12 possible resolutions (one for each chromatic scale degree), different texts contain different numbers of possible resolutions of the augmented sixth. For instance, the Kostka-Payne has 8 difference resolutions, MusicTheoryExamples.com has 10, and the YCAC has 129. However, because the normalized entropy equation uses the number of outcomes to calculate maximum entropy, we can comfortably compare the entropy of different corpora containing different numbers of outcomes.
Return to Text -
Importantly, I am not arguing that these experimental sections will always be the last chronological subsections of a corpus, nor am I arguing that there will be only one such section. A textbook that, for instance, highlights the works of experimental composers of the early Renaissance, late Baroque, and late Romantic would have several less-disciplined subsections of that corpora disposed across centuries, unlike the more directional trends observed in the current essay. Equating a march toward increasing chromaticism with historical teleology seems to be a problematic aspect of many of the corpora under consideration (pedagogical and otherwise); such issues will remain for future analyses.
Return to Text
REFERENCES
- Aldwell, E., & Schachter, C. (2003). Harmony and voice leading (4th ed.). Boston, MA: Schirmer.
- Baker, D. (2019). Modeling melodic dictation. Doctoral dissertation, Louisiana State University, LA. Retrieved from: https://digitalcommons.lsu.edu/gradschool_dissertations/4960/
- Baker, D. (2021). MeloSol corpus. Empirical Musicology Review, 16(1), 106-113. https://doi.org/10.18061/emr.v16i1.7645
- Bellmann, H. (2005). About the determination of key of a musical excerpt. In R. Kronland-Martinet, T. Voinier, & S. Ystad (Eds.), Computer modeling and music retrieval (pp. 76-91), Berlin, Germany: Springer-Verlag.
- Berkowitz, S., Fontrier, G., Kraft, L., Goldstein, P., & Smaldone, E. (2011). A new approach to sight singing (5th ed). New York, NY: W.W. Norton.
- Byros, V. V. (2009). Foundations of tonality as situated cognition, 1730-1830: an enquiry into the culture and cognition of eighteenth-century tonality with Beethoven's Eroica Symphony as a case study. New Haven, CT: Doctoral dissertation, Yale University.
- Cuthbert, M. S., & Ariza, C. (2010). music21: a toolkit for computer–aided musicology and symbolic music data. In J. S. Downie & R. C. Veltkamp (Eds.), Proceedings of the 11th Conference of the International Society for Music Information Retrieval, (ISMIR) (pp. 637–642). Canada: ISMIR.
- Devaney, J., Arthur, C., Condit-Schultz, N., & Nisula. K. (2015). Theme And Variation Encodings with Roman Numerals (TAVERN): a new data set for symbolic music analysis. In M. Müller & F. Wiering (Eds.), Proceedings of the 16th Conference of the International Society for Music Information Retrieval (ISMIR) (pp. 728–34). Canada: ISMIR. https://doi.org/10.5281/zenodo.1417497
- Ewell, P. (2020). Music theory and the white racial frame. Music Theory Online, 26(2). https://doi.org/10.30535/mto.26.2.4
- Huron, D. (2006). Sweet anticipation: music and the psychology of expectation. Cambridge, MA: The MIT Press. https://doi.org/10.7551/mitpress/6575.001.0001
- Kim, J. C. (2011). Tonality in music arises from perceptual organization. Doctoral dissertation, Northwestern University, IL. Retrieved from: https://www.proquest.com/docview/872077197?pq-origsite=gscholar&fromopenview=true
- Krumhansl, C. L., & Kessler, E. J. (1982). Tracing the dynamic changes in perceived tonal organization in a spatial representation of musical keys. Psychological Review, 89(4), 334–368. https://doi.org/10.1037/0033-295X.89.4.334
- Krumhansl, C. L. (1990). Tonal hierarchies and rare intervals in music cognition. Music Perception: An Interdisciplinary Journal, 7(3), 309–324. https://doi.org/10.2307/40285467
- Laitz, S. (2012). The complete musician: an integrated approach to tonal harmony, analysis, and listening (3th ed.). Oxford, England: Oxford University Press.
- London, J. (2013). Building a representative corpus of Classical music. Music Perception, 31(1), 68-90. https://doi.org/10.1525/mp.2013.31.1.68
- Margulis, E. H. & Beatty, A. P. (2008). Musical style, psychoaesthetics, and prospects for entropy as an analytic tool. Computer Music Journal, 32(4), 64-78. https://doi.org/10.1162/comj.2008.32.4.64
- Quinn, I. (2010). Are Pitch-Class Profiles Really "Key for Key"? Zeitschrift der Gesellschaft für Musiktheorie, 7(2), 151-163. https://doi.org/10.31751/513
- Quinn, I., & Mavromatis, P. (2011). Voice-leading prototypes and harmonic function in two chorale corpora. In C. Agon, E. Amiot, M. Andreatta, G. Assayag, J. Bresson & J. Manderau (Eds.), Mathematics and computation in music: proceedings of the third international conference (pp. 230-240). Berlin, Germany: Springer-Verlag. https://doi.org/10.1007/978-3-642-21590-2_18
- Quinn, I. & White, C. (2017). Corpus-derived key profiles are not transpositionally equivalent. Music Perception, 34(5), 531–540. https://doi.org/10.1525/mp.2017.34.5.531
- Saffran, J. R., Aslin, R. N., & Newport, E. L. (1996). Statistical learning by 8-month-old infants. Science, 274(5294), 1926–1928. https://doi.org/10.1126/science.274.5294.1926
- Schaffrath, H. (1995). The Essen Folksong Collection in Kern Format [Computer Database]. D. Huron (Ed.), Menlo Park, CA: Center for Computer Assisted Research in the Humanities.
- Temperley, D. (2007). Music and Probability. Cambridge, England: The MIT Press. https://doi.org/10.7551/mitpress/4807.001.0001
- Temperley, D. (2009). A statistical analysis of tonal harmony. Retrieved from http://davidtemperley.com/kp-stats/
- Temperley, D. & Marvin, E. W. (2008). Pitch–class distribution and the identification of key. Music Perception, 25(3), 193–212. https://doi.org/10.1525/mp.2008.25.3.193
- White, C. (2014). Changing styles, changing corpora, changing tonal models. Music Perception, 31(3), 244-253. https://doi.org/10.1525/mp.2014.31.3.244
- White, C. & Quinn, I. (2016). The Yale-Classical Archives Corpus. Empirical Musicology Review, 11(1), 50-58. https://doi.org/10.18061/emr.v11i1.4958
- White, C. (2018). Feedback and feedforward models of musical key. Music Theory Online, 24(2). https://doi.org/10.30535/mto.24.2.4
- Zajonc, R. B. (1968). Attitudinal effects of mere exposure. Journal of Personality and Social Psychology, 9(2, Pt.2), 1–27. https://doi.org/10.1037/h0025848