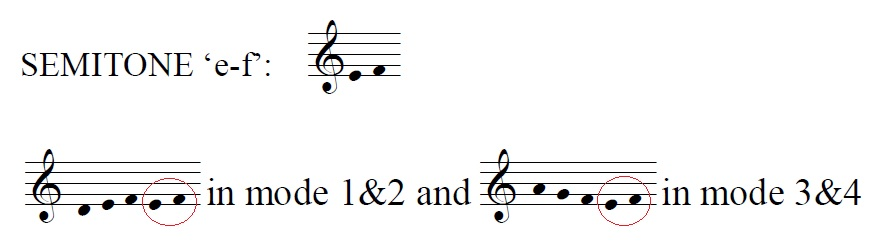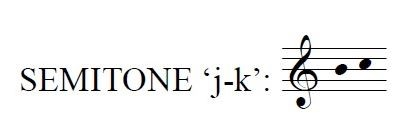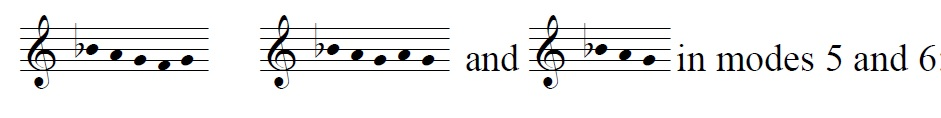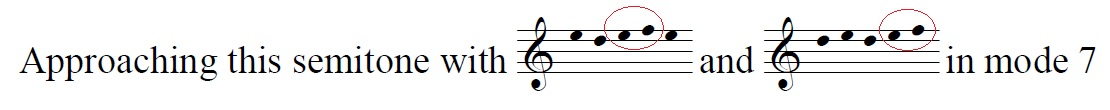TO understand the musical world of medieval monasteries, and the repertoire developed in them that would one day come to underpin much of the early polyphony in the West, musicologists must reconstruct the same natural familiarity with the chants that the monks and nuns had. This is easier said than done. There are thousands of extant melodies associated with these chants and the sources containing them are scattered across scribal traditions, monastic conventions, liturgical occasions, and larger cultural contexts. In recent decades, scholars have turned to electronic databases and online collaborative indexing projects, such as CANTUS, to approximate an overview. The Melodic Construction and Evolution in Late Medieval Saints Offices project has developed computational algorithms to apply to the analysis of chant melodies on a scale larger than what is possible for any single musicologist working alone. We understand our work to be only the first steps in a new direction in which overall tendencies and statistical likelihoods color and inform our idea of the medieval musical impulse. To see how the Gregorian tradition reflects this general human impulse to build meaningful melodies out of familiar gestures is to connect our musical history to (Western, European ideas about) 'Musicality' itself. Our approach is analogous to corpus studies in linguistics, in that it considers patterns in a large body of texts as evidence for the tacit knowledge – or, in our case, musical assumptions and expectations – about the subject in question. By applying data analysis techniques that originated in other fields of study to strings of musical data, we approach the question of melodic structure, and a melody's relationship to its modal associations, on a new and larger scale than ever before. The results of the current study are based on a pool of 5,906 individual melodies of chants from the Western, medieval, Christian monastic traditions across Europe, although mainly confined to Office chants (i.e., responsories, verses, antiphons, etc.) The database listing these chants is found on Github (https://github.com/schindlerjake/The-Sticky-Riff). We took several steps to extract data from the Hughes text file database to make it usable in our analysis of these chants, ultimately extracting each chant and entering them into our own CSV file to create our database. We used python programming to strip all the data for each chant from the Hughes database, including metadata on each chant and different ways of noting the pitches. The Hughes database notated the chant using 'scale degrees' relative to the mode and Final of the chant. The column in our database that holds the text string from the Hughes database is 'Chantwords'. To represent each chant in Volpiano we wrote a python program to take this chant with its mode and Final and translate it to a Volpiano notation separated by each sung word. For instance, gloria.13.21.2 sanctoruM.10,.121.1 in mode 1 with a Final of D becomes d-f-e-d-e—-d-c-d-e-d-d. The main body of the repertoire studied here is Andrew Hughes' transcriptions of chants for late medieval saints, published in his two-volume Late Medieval Liturgical Offices (1994, 1996). These have been largely overlooked by the scholarly community because of the idiosyncratic way Hughes encoded them in his electronic databases in the 1990s. However, the consistency of his encoding makes them ideally suited for computer-assisted analysis. Considering these melodies as a sequence like any other, such as a string of DNA or a sentence made out of words and letters, we can use computational tools to identify more sophisticated melodic patterns and explore the idea that these melodic patterns are the result of a musical culture of expectations and cues that would have informed both composer and singer. This undertaking marries computer science and medieval music in a new way, reframing the scholarly questions and sharpening our definitions of historical musical convention.
Andrew Hughes was a pioneer in connecting computing and information science to medieval musicology in the 1980s and 1990s when the application of these fields in the humanities was quite rare. Although the musicological community around him did not immediately take up his methods, he saw that one of the main problems for medievalists is the unwieldy nature of their subject, which spans almost one thousand years and reaches across (and beyond) the entire European continent. The computer offers the researcher a way to catalogue, compare, and analyse materials on scale that is literally 'inhuman'. In the last quarter of the 20th century, Finn Egeland Hansen was one of the only other medieval musicologists to emphasize the role of a computer in his The Grammar of Gregorian Tonality (1979). It would take another decade before Ruth Steiner began the CANTUS project out of a compilation of several indices of chant manuscripts into a single database and caught the imagination of chant scholars around the world. This project, now online and renamed the Cantus Database, has set the standard for other projects that use computer technology to enhance medieval musicology including the Cantus Index, the Portuguese Early Music Database, Cantus Ultimus, the Hungarian Chant Database, Fontes Cantus Bohemiae, Cantus Planus in Polonia, Comparatio, Musica Hispanica, Académie de chant grégorienne, and Antiphonale Synopticum. These projects, ground-breaking as they are, focus predominantly on chant texts and the chants' positioning in medieval rituals; most databases contain comparatively few melodies. Recent work, under the name of the Ariadne Project, by Morné Bezuidenhout and Mark Brand focuses on the late medieval repertoire, developing a computerized method to look for melodic characteristics of late chant. So far, however, this has been restricted to a comparatively small number of chants and their methodology involves looking for specific characteristics in the melody already isolated by previous scholarship. The current study approached a large body of chants and considers the melodies 'bottom-up', allowing the usual cycle of analytics / interpretation to begin with the data presented by the chants themselves and not the assumptions and 'hunches' of musicologists. To date, melodic analysis of chant is usually confined to a sample of perhaps as many as several hundred melodies, if not fewer, and are conducted on a single genre of chant. Analyses are then further delineated by mode, monastic order, era, text, etc. Recent publications concerning Offertories (Maloy, 2010), Tracts (Hornby, 2002, 2009), Graduals (van Deusen, 1972), Responsories (Helsen, 2008), and Antiphons (Nowacki, 1980), have analysed anywhere from about 50 to 900 chants at a time, depending on genre scope. The larger the sample size, of course, the more confidently musicologists may make generalized observations about musical tendencies, usually tied to mode. These analyses are useful in determining common musical turns of phrase that might characterize a genre or style, and within those genres, typical forms may start to take shape. This allows us to the call attention to specific chants that deviate from the more regular forms in some way. Generally, then, this type of analysis has afforded a deep understanding of particular types of chant, but since they have been studied in isolation, they are necessarily removed – at least partially – from their original liturgical contexts, where different types of chants coexisted quite closely and naturally, even though the age and style of their compositions might be quite varied. The kind of cross-genre melodic analysis in this project is therefore rare – the kind of thing usually only suggested as possible in the future – and has never been conducted on the scale of seven thousand melodies, across all the modes, at once. In seeking to clarify how Gregorian chant was heard, remembered, written down, and taught over the centuries, we need to take as broad a view as possible, using as much data as we cannot so we can be correct in every instance, but so that our tools and analytics can formulate a kind of 'familiarity' with the repertoire today that we can no longer naturally cultivate through repetition and ritual.
Conceiving of the Gregorian tradition as part of a more global corpus of musical prayer and meditation reveals that similar studies have been undertaken to understand analogous musical repertoire, such as classical Indian ragas (Nylund, 1983) or Arabic maqām (Shymays, 2013). Many features of the Gregorian repertoire, such as the presence of stereotyped melodies or recurring riffs, fits into a larger world of music conceived within a primarily oral culture. Even apart from the spiritual and ritualistic world, we find promising signs of the central importance of these 'riffs' in the birthplace of the word itself: jazz (Broze and Shanahan, 2013). Computational approaches now allow medieval musicology to consider the thousands of monastic chants left to us in a broader, more universal context of the meditative, intimate expression of the human desire to make music at all. The objectivity afforded the researcher who considers thousands of chants points to a common instinct for melody building which is often seen as subjective or particular to one tradition. The more we know, the more we can see how connected we have always been.
METHODS
Preliminary Work
INITIAL N-GRAM ANALYSIS AND GRAPHS
The regularity we observe in the melodies of most music (acknowledging that there exist exceptions, especially amongst contemporary composers such as Xenakis who frequently set out to reject precisely this regularity) are a consequence of structural constraints on the formation of melodic sequences. We can profitably view these constraints as analogous the syntactic and morphological rules that inform the generation of parse-able utterances in natural language. With this parallel in mind, we borrow the tools and techniques of contemporary natural language processing (NLP) to interrogate the chant melodies.
Perhaps surprisingly, many of the most powerful tools in modern NLP are based on the extremely simple technique of "n-gram analysis", a method for decomposing words, and longer sequences of characters into a form more amenable to analysis by modern machine learning techniques. A 1-gram is a single character (e.g., 'a' or 'z'); a 2-gram is the juxtaposition of two single characters (e.g., 'ab' or 'cz'); and so forth. A given block of text can be analyzed by fixing some integer n and counting the number of occurrences of every 1-gram, 2-gram… n-gram in the text. This list of occurrence counts can then be composed into a vector of integers which describes how often each n-gram appears in the block of text. We now have a means of converting any block of text into a vector of fixed dimension and, consequently, we have a tool for comparing two texts: convert each to a vector, and compare the distance between the two vectors.
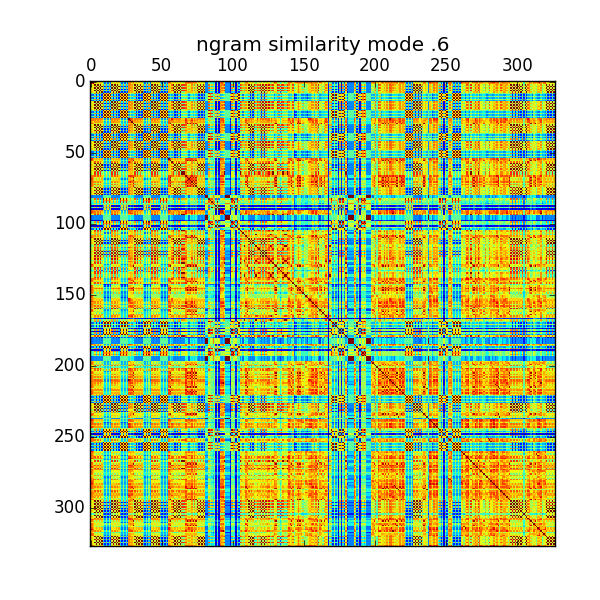
We applied precisely this approach to the analysis of the chant corpus. Each chant was converted to a vector by counting the number of occurrences of each 1-gram, 2-gram, 3-gram and 4-gram – viz., we recorded the number of times each short melodic sequence occurred in the chant. We then computed the 'distance' between any two chants as the cosine similarity between their associated vectors. The result of these comparisons can be seen in Figure 1 in which the 780 mode 6 melodies were compared to each other for structural similarities. Each row, and the corresponding column, represent one chant. The color of the matrix entries describes the distance between every pair of chants. Even a cursory glance at this matrix, with no further analysis, shows manifest evidence of structure and varying degrees of relatedness between chants.
To investigate this structure further, we turned to network theory. A network is composed of nodes – drawn as dots and representing objects – and edges which connect nodes that are related; in our work, each node represents a chant. If two chants are 'close enough' 2 to each other, we connect them via an edge. The network theory literature provides us with a host of algorithms for community (or module) finding in these graphs. We employed here a simple Louvain module-finding algorithm and visualize the results in Figure 2.
Displaying melodic comparisons as matrices showed us that there were aspects of the melodies themselves, beyond their vertical range or frequently-repeated pitches, that distinguished mode from mode. That is, the matrices confirm the presence of modally specific musical gestures or turns of phrase, even without identifying which of these are particularly popular, or what sort of distribution these familiar turns of phrase might have. When the same comparisons are displayed as a network, we are able to get a sense of the kinds of groups of similar chants and the various relationships that may exist between them. For example, in Figure 2, above, we note that a handful of melodies (shown in red) have connections to both of the most densely populated groups of similar chants (shown in green) and are less directly related to a third, blue group (at about '2 o'clock' in the network.) Several other groups of similar chants do not seem to be related to the main group at all. Is this a function of the genres of chants being compared? Or perhaps a result of geographical preferences for certain 'riffs' over others, even within one mode? Theoretically, it would have been possible to isolate each interesting node in these networks and refer to the main Melodic Evolution database to determine the chant's identity and source, to build up a larger and more inclusive picture of melodic comparisons across European manuscripts according to mode. However, we are more interested in determining which overall musical impulses come to the fore as a result of the comparison, since we are not bound by the capacity of a single human researcher to keep accurate information about thousands of chants.
RECURRENT NEURAL NETWORKS
Neural networks – despite the media hype and unrealistic comparisons to biological brains – are simply convenient tools for learning, and representing, complex probability distributions in a compact format. Recurrent neural networks (RNNs) employing long-short term memory (LSTM) are well-suited to learning the statistics of sequences and, as a generative model, can then create new sequences that obey the previously-observed statistics. RNNs have been more traditionally used in language studies, where the grammar and vocabulary learned from excerpts of natural language serve as the basis for new and creative suggestions.
We trained an RNN on the chant corpus and then prompted the RNN to generate new sequences, which displayed many of the hallmarks of a typical late medieval chant. Most arresting was the RNN's inclusion of short melodic gestures that were very similar to differentiae, which are short (usually 5 or 6 pitches) 'riffs' given at the end of an antiphon to indicate which tone should be used for the singing of its psalm pair. This was particularly unexpected because differentiae are not included in the dataset that the RNN learned from. While this production of 'robot chant' might seem little more than a party trick, it is meaningful. Indeed, the generated sequences are a window into the statistical patterns learned from the training corpus. The RNN has no knowledge of the rules of chant, no formalized encoding of the syntax, and no means to comprehend the semantics; it is a purely statistical artifact. It is, nevertheless, able to recreate apparently authentic sequences which any medieval monk or modern scholar would recognize as a psalm tone cadential formula. This means that these 'riffs' must be embedded in the melodies of the antiphons and responsories sung in the same contexts as the psalms, for them to be 'learned' by the RNN. For example, in Figure 3 the last three, short 'riffs' in mode 7, generated by the RNN, would remind anyone at all familiar with the tradition of psalm tone Differentiae. The longer melodies, shown above the three short ones in Figure 3, also bear a startling resemblance to a real mode 7 melody in terms of where the intervallic leaps fall, how cadences are approached, and the number of repeated pitches allowed before motion up or down is required. (See Figure 4.)
Main Experiment
In conducting the initial investigations into the data set, we preserved the usual practice of defining melodies according to their modal assignments, even though this kind of classification becomes increasingly spurious near the end of the Middle Ages. It is, of course, well known that melodies in the same mode seemed to use melodic gestures or formulas - "riffs" - in strategic places; these riffs often surfaced, unsurprisingly, in the RNN-generated samples, confirming their frequency (and therefore prominence) in the repertoire. But could we use the recognizable riffs to identify the mode of a melody? This way of understanding the construction of mode – that is, from the riffs to the scales, and not the other way around – mirrors more closely how scholars believe the system of church modes originated in the Oktōēchos, with melodic identity determined by the arrangements of tones and semi-tones in a tetrachord. (Jeffery, 2001) The core identity of the tetrachord is found in its placement of the semi-tone, as discussed by Jean Claire. (1962, 1963) When considering the origins of the Gregorian modal system, we are never far from invoking the nine Psalm Tones, each of which feature a characteristic melodic flourish, called a Differentia, at the end of each line of chanting. These Differentiae 'differentiate' each of the modes by associating certain melismatic endings with particular Psalm Tones. By giving only these last few notes of the melodic line - usually not more than six pitches - in the manuscript, the scribe can signal to the singer which modally-appropriate Psalm Tone to sing. There are several differentiae per mode and most distinguish themselves from the others, aurally, through a gesture that includes a semitone. (Even the differentiae which do not include a semitone are therefore also aurally identifiable as different from the others that do.) Medieval singers spent more time with Psalms than any other form of chanting, and this way of intuiting modal association from the presence of the semitone would become natural very quickly. Therefore, by identifying the occurrences of semi-tones in the melodies in our database, regardless of mode or genre, and looking at them as defining features, we might allow the chant to 'speak for itself' in terms of the musical relationship between riff and mode. This bottom-up understanding of modal systems in Gregorian repertoire is reminiscent of similar ideas about repeated musical gestures in Indian classical music or the maqām system of the Islamic Orient.
FOCUS ON SEMITONES AS 'FLAG' FOR MODALLY CHARACTERISTIC SUBSTRINGS
When presented with the amount of melodic data found in Hughes' collection, a natural first impulse is to search for riffs that recur at key points in the chant, or to look for particular association between text and melodic setting. Indeed, the initial experimentation with the data shows that these melodies are rich in patterns and intentional similarities, but those with any experience with medieval chant will know this from experience. Incipits and cadences are highly stereotyped and use immediately recognizable musical formulas to signal phrase beginnings and endings, and basic searches will reveal the notable extent to which they characterise the late Medieval repertoire. However, these tend to be used for structural reasons as opposed to musical ones - that is, it is much easier to find a recurring phrase at the end of a phrase and be certain that its function is to signal that end to the singers and listeners than it is to understand what function a frequently-heard riff in the middle of a phrase might have. Since the RNN revealed only frequent strings of pitches and did not attend to melody structure or associate recurring riffs with particular structural parts of the line, this indicates that we should not look only at frequency of riff - since this will undoubtedly give us incipits and cadences - but also melodic characteristics of the riff, no matter its order in the musical phrase.
To shift focus away from pure frequency and towards a view that might enable us to see how riffs build modes, it was determined that using the occurrence of semitones in each melody would be a musically sensitive method that did not privilege place over other factors. If we were to be able to determine how a semitone was approached and left, at every transposition in which semitones occur, perhaps there would be patterns that would help us understand how the RNN could have generated riffs that resemble differentiae so closely. After isolating each semitone usually present in medieval manuscripts (both ascending and descending), we ran an algorithm through the melodic strings to rank the most frequently used ways to approach and leave each occurrence of a semitone. Very quickly, we learned that Hughes' fidelity to the manuscripts from which he copied posed a hidden problem for the present inquiry: quite often, b-naturals on the page would have been modified to be sung as b-flats, based on solfege practice of the time. We would first need a way to determine if a b-natural in the data was to be interpreted as such or not, and that the accuracy of this determination would determine the fate of the inquiry.
FICTA B-FLATS AND HOW TO FIND THEM
Hughes' chant melody strings in his LMLO contain b-flats only when they are physically present in the manuscript. Hughes (1996) explains that this accidental's haphazard appearance, " – here in one version, there in another, absent in a third – seems to depend partly on the expertise of the singers in applying rules well-known then but little understood now" (p.176). Although Carvell (1988) points out that the solfege rule 'Una nota supra la semper est canendum fa' seems to have taken shape around the time of Tinctoris' 15th-century music theoretical writings, the medieval placement of the flat sign – almost always on 'b' – indicates that singers understood some rules pertaining to flats implied in particular hexachords, even when chanting in unison and in no danger of flirting with outright dissonance. Zippe (2001) has demonstrated that certain neume patterns in early medieval manuscripts seem to imply a flattening of the 'b' which appears in later manuscript cognates. The challenge then becomes formulating these flat rules in way that a computer can deterministically apply them to our collection of almost 6,000 melodies.
Our initial investigation began with creating two tools to gather broad information about trends in the dataset. The first, to find the most commonly occurring substring by mode with any specified length (MostCommon), and the second, to find the most commonly occurring substrings preceding and proceeding any given string regardless of mode (STSearch). The role of these tools was to be a starting point in identifying characteristic riffs for each mode. Both tools were scripts written in python and pulled data from our database of melodies. We analyzed the melodies as a Volpiano string of characters. (The font, Volpiano, was named after the 11th-century priest and building contractor, William of Volpiano, whose tenure in St. Bénigne in Dijon is associated with an impressive, fully notated Tonary which indicates exact pitches using alphabetic letters together with neumes. The font is useful when dealing with large numbers of melodic strings because instead of repeating the alphabet after 'g', as is expected in musical contexts, it continues with 'h' as what would usually have been 'a' again. This way 'c' is distinguishable immediately from 'k', etc. It is available at http://fawe.de/volpiano/.) After running MostCommon.py to look for the most common substrings of length 3, we recognized a possible limitation with our results—b-flats were not represented in our dataset. 60% of mode 1 chants (754 of 1259) and 53% of mode 5 chants (265 of 498) had at least one instance of the riff 'a-b-a' ('h-j-h' in Volpiano). Additionally, when isolating mode 6 chants transposed to c, the riff 'b-c-c' appeared in 51% (158 of 308) of the melodies. Both of these riffs commonly flatten the 'b'—'h-j-h' due to solfege rules in mode 1 and 2 as well as the tendency of avoiding the tri-tone in mode 5 and 6, and 'b-c-c' as the common Galician Cadence where the Final is approached by its lower whole-tone neighbor.
The rules, as formulated below, divide b-flats into three conceptual identities: Real, Implied, and Associated. The flats that we encounter in the manuscript sources, as transcribed by Hughes in the LMLO, we call "Real". "Implied" flats are those not given in the manuscript but which should be sung anyway, in reference to either the hexachord to which they belong and in which they are contextualized in time, or the presence of the 'Gallican', late medieval cadence in which the (usually repeated) Final is approached from a tone below (Hankeln, 2008). We call a third kind of b-flat "Associated" because it is tied to either a Real or an Implied flat in a way that causes some doubt that singers would have adjusted pitch to suit the rest of the phrase containing the other flattened pitch. For example, in a case where the top of a hexachord gives us an implied flat (following "una nota supra la"…), what is a singer likely to decide about that pitch four or five notes later, before completing the musical phrase?
After much experimentation, we have arrived at the following heuristic for determining b-flats as they may or may not be written in the manuscript source. They are given in the End Notes. 3 These classifications of flats—Real, Implied, and Associated—are a way of attempting to capture the process a singer familiar with the conventions of their time goes through to determine whether to sing what they see on the page, or to 'correct' it to be what they know should be sung. The haphazard placement of flats and lack of formal notation rules in the source manuscripts introduce a significant challenge with a large dataset. It is insufficient to rely only on the 'Real' flats because the author's intent is not always clear when a flat is notated, and so new heuristics must be developed, as shown above. What follows are some examples of the process of creating and testing our algorithm. In the following examples, '<' represents a flat sign found in written in the manuscript and ';' represents the end of a phrase notated with a rhyming word in the manuscript.
The newly-composed Responsory verse tone in mode 1, beginning, "Nec est frustratus eius affectus" for the feast of Adalardus (for the responsory, Regali stirpe nobilitatus,) presents a good opening case study outlining the effectiveness of the heuristic for assumed b-flats. The first phrase of this verse has a notated flat before the fifth word, and therefore it is natural to assume that a b in that word is flattened (a 'real' flat). There are 'b's prior to the flat sign as well, but it is unclear if those should also be flattened. Through experiment, we have determined that any rule we could apply to address these b's prior to the written flat would result in over-correcting, and so none have been applied. However, later in the melody, the 'a-b-a' motion (highlighted in red) in its particular context, which is arguably back down in the hexachord from which it began, has lead us to flatten this b because of the solfege rule about "one note above 'la'. Several pitches later, another b is found in an ascending scale to c and then studiously avoided for the rest of the chant. We have determined that flattening it would imply a more liberal sprinkling of flat-signs than may be realistic, so we understand this section of melody to maintain its b natural, since there is no especially compelling reason to consider it a b flat.
There are also examples where the written flats from in the original manuscript don't make musical sense. For example, Hughes' transcription of the 6th-mode antiphon for St. Cuthbert, Mox pater suos affatur, found in the Worcester Antiphonal, among other manuscripts, the flat sign is given (shown below as '<' which is Hughes' method of displaying the flat sign) after the opening three words. However, the next word does not include the pitch 'b'. Did the scribe intend for later 'b's to be flattened? A case can be made for flattening the 'b's in the second full phrase, but it is not until the movement 'a-b-a', descending into the D-hexachord, that we can be relatively sure a b-flat would have been added by the singer, even if omitted by the scribe.
It is also important to recognize that it is not as straightforward as simply assuming that all instances of 'a-b-a' should be a semi-tone, regardless of the presence of a flat sign. In the verse tone for the mode 5 responsory for St. Hedwig, Manus beate Hedwigis, the first instance of 'a-b-a' (highlighted in red) does not belong to a D or F hexachord and flattening the 'b' here might be presuming too much. Therefore, we have erred on the side of caution, and only added an extra flat to the 'b' three pitches from the end of the verse, since the 'b' earlier in the same word was explicitly signed (shown in red.)
RESULTS
After applying the flat-sign heuristics to the dataset, we were in a position to examine semitone negotiation across thousands of melodies. Could it be that the placement and treatment of this interval came to characterize, or identify, one mode from another, even if this was not something the average singer would have been able to consciously articulate? After all, if melodies could be transposed to different Finals (something frequently found in late medieval books) the only way to differentiate one mode from the others were the locations where the semitones were encountered, relative to the Final and the Reciting Tone. Would the traditional forces of an older, aural musical culture, such as stereotyping and formulaic expressions, be detectable at semitones? To investigate this, we looked for all instances of any of the possible semitones in the medieval gamut (that is, A-Bb / Bb-A; B-C / C-B; e-f / f-e; a-b-flat / b-flat-a; b-c / c-b; e1-f1 / f1 - e1) and tracked the pitches preceding and following each semitone, according to the mode of the melody. For example, the semitone 'e-f' is followed by 'e' 50% and 45% of the time in modes 1 and 2, respectively, whereas the same semitone is followed by 'g' 47% of the time in both modes 3 and 4. This investigation was conducted with a Python script (STSearch) to find all preceding and proceeding riffs from a given substring. We had a number of parameters to set, including how long the preceding and proceeding strings were to be, whether or not the algorithm should look across words, and what kind of statistical result we wanted to produce.
We looked mainly at preceding and proceeding strings of length 1 and of length 3. Length 1 strings show by what note a semitone is immediately approached. Length 3 strings show more specific trends in the data. It was found that length 4 strings were too sparse in the dataset to produce statistically meaningful results—most of the results appear in less than 5% of the instances found. It was decided that the algorithm should not look across words for preceding and proceeding strings so as to respect the natural way music and its text are conceived together, in chant. The natural separation of words acts as a significant separator for these riffs.
We looked at each proceeding and preceding result in three ways: (a) as a percentage of total instances of the semitone, (b) as a percentage of that substring in each mode, and (c) as a percentage of instances of the semitone in each mode individually.
- (a): One percentage per riff, regardless of mode:
- (b) By appearance: How prominent is the proceeding or preceding riff among modes?
- Mode 1 = , Mode 2 = , etc.
- (c) By mode: How prominent is the proceeding or preceding riff in each mode individually?
- Mode 1 = , Mode 2 = , etc.
Data was gathered from STSearch for all semitones. While no riff is unique to a particular mode, we have found some noteworthy examples that show riffs contributing to the character or identity of certain modes, through its frequency of use and, occasionally, the stability of its placement in the overall course of the melody / text-setting. The following discussion itemizes a few of these, identified by the semitone embedded in them and illustrates how they may be understood as modal identifiers. In general, the percentages given below must be read in the context of the calculations outlined above, that is, they are (modally and gesturally) context-specific. We have identified the most prominent examples of gestures that characterize the modes in which they are found and presented them here. For a full list of every identified 'riff', please refer to the Github for this project, mentioned above.
Though it only appeared in 4.34% of the overall instances of riffs that approach 'f-e', the riff 1-d-e-f-e-f was found 94.9% of the time in chants in the Protus modes (1 or 2). Contrasted with this, the riff 1-h-g-f-e-f was found 35% of the time in mode 3 and 4 chants, but only 25.4% of the time in mode 1 and 2. In other words, chants in modes 1 and 2 tend to approach the 'f-e' semitone from below whereas in modes 3 and 4, they tend to approach from above.
Although the difference is small between these two riffs (simply the addition of C in the riff identified in mode 6 chants), it is revealing to consider the statistics of their appearances in chants of these two modes. 1-e-f-e-d- (at the end of a phrase or, at least, word of text) appears in 55.8% of mode 1 melodies and only 2% of mode 6 melodies whereas the riff 1-e-f-e-d-c- appears 31.7% of the time in mode 6 and 22.4% in mode 1 (That is, in mode 1, it is less common to continue the descending motion with a C than it is to stop it at D.) The additional pitch 'C' plays a very different role in mode 6 than in mode 1, because of its intervallic relationship two the Finals of these modes, and the relative importance of the pitch C in mode 6, especially in the later medieval repertoire, when perfect fifths were coming to dominate cadential sonorities in general. (Hughes, 2011)
In 37.3% of the occurrences of the semitone 'j-k' in mode 3, it is found at the beginning of a word. Perhaps this impulse can be explained by the fact that the Reciting Tone in mode 3 is c (or 'k' in Volpiano) and invoking the ascending semitone here draws attention to the prominence of the upper note of the pair.
It is also interesting to note that chants in mode 3 are likely to use this ascending interval as a marker for a switch in direction; 1-j-k-l-k-j- appears in 14.9% of mode 3 melodies and 1-j-k-j-h-g- in 15.2%. Chants in mode 5 share with mode 3 their Reciting Tone of 'k', but have a Final of F instead of E. When this semitone is found in mode 5, only 9.6% of words containing this semitone use it to begin the word, meaning it is not as significant a tonal marker in this mode for the Reciting Tone. Further study will be necessary to determine whether the tritone relationship between mode 5's Final (F) and the 'j' above it play a role in its avoidance of this semitone, compared with its melodic cousins in mode 3.
Approaching the semitone with 1-h-g-h-ij-h is seen in mode 1 chants 41.9% of the time (and 21.8% of the time in mode 5). However, approaching the semitone with 1-k-ij-h- or 1-k-l-k-ij-h- is seen 53.6% and 50.8% of the time respectively in mode 5. Here again, the direction from which the semitone is approached can be understood to 'signal' where the singer is relative to the Final of the mode in question.
This pattern signals the end of a word more than 37.55% of the time across any mode. As one might expect, chants in mode 1 are permeated with this semitone much more than other modes; omitting the repeated 'h', mode 1 chants feature this semitone without the repeated pitch at the ends of words 48.6% of the time, but with the repeated 'h', this number rises to 75.3% of the time! The prominence of mode 1's Reciting Tone ('h') in the later medieval repertoire (and even, to some extent, in the earlier layers) explains this phenomenon, but it is interesting to see our general impressions of melodic tendencies borne out in statistics derived over a corpus of thousands of chants.
Whereas in mode 1 melodies treat this semitone as a signal that a word is ended, in modes 5 and 6 it is often followed by a 'g' and used as a signal to continue across the word or phrase where it is found. The riffs shown directly above are found mainly in modes 5 / 6 for these purposes. In mode 5, one of these three riffs follow the
1-ij-h- semitone 29.6% of the time, and in mode 6, this number increases to 39.4%.
Approaching the semitone 'n-m' with the riff 1-k-l-m-n-m- appears 69% of the time in modes 5 and 6. Of course, this riff includes the same semitone articulated in reverse order: 'm-n'. The riff 1-k-l-m-n- (that is, the simple ascending line to the upper octave of mode 5's traditional ambitus) appears 83% of the time in modes 5 and 6. This scalar approach from below, and the use of the 'm-n / n-m' semitone as the apex of such movement, seems to have been very closely connected with the overall feel of chants in modes 5 and 6 for late medieval singers.
The two approaches shown directly above are very characteristic, statistically speaking, of mode 7 melodies.
1-m-l-m-n-m- appears 63.5% of the time and 1-m-n-o-n-m- appears 71.6% of the time. The ascending version of this semitone 'm-n', is approached with a zigzag motion of 1-l-m-l-m-n- in mode 7 an impressive 84.7% of the time.
DISCUSSION
It may seem strange to take a strictly empirical approach to something as nebulous as musical intuition about modes, especially the kind of centuries-old musical intuition that comes to us through extant sources. The variance between manuscript readings, the uncertainty about performance conventions, and even the likelihood of mistakes or omissions in the data itself, all warn against making too many assumptions. However, the scale of our corpus ensures that the presence of occasional individual errors contributes only a small amount of 'noise' to an overwhelmingly strong statistical signal. Only a decade ago it was rare to find genre studies or comparative analysis that included more than several hundred melodies. The present study looks at 5,906 chants across all the genres sung for the Office, found across Europe, spanning several centuries, at a level of detail that was impossible in Hughes' time, although obviously not inconceivable. Hughes collected and curated this data for just such a purpose. By isolating particular 'riffs' that characterize modal idioms and tracing their appearance through a large dataset, we begin to be able to 'zoom out' far enough to make the kinds of observations about medieval musical tendencies, assumptions, and preferences that Hughes, and other scholars of his generation, had hoped would be possible, based on their work. At the base of a chant scholar's work is an ever-present doubt about how much we can trust our own musical impulses and assumptions to be like those of medieval singers. The more we can replace our own conjecture with hard evidence about their musical world, and the more robust and expansive that evidence becomes, the greater our ability, as scholars, to stay true to the world we wish to explore. The idea of musical modes originated as sets of recognizable turns of phrase that were distinctive from each other in pitch order and relationship has been suggested in various ways over decades, but now our initial findings support this idea with empirical data. Given that most of the melodies considered in this dataset come from the late medieval, musically literate time period in which modes were fixed and well understood theoretically, it is evident that these (originally unwritten) musical gestures are still present at a structural level and revealed when considered and compared in their thousands. These 'sticky riffs' are usefully understood as core components of a singer's idea of a modal system of chant and the melodies afforded by it.
ACKNOWLEDGMENTS
The authors would like to acknowledge the work of many research assistants who helped with the clean-up and curation of Hughes' dataset as published in his Late Medieval Liturgical Offices, most notably the extensive work of Jason Mile and, in the context of another transcription project as part of the Single Interface for Music Score Searching and Analysis (SIMSSA) project, Yaolong Ju. We are grateful for Jonathan De Souza's input concerning corpus analysis methodologies at the beginning stages of this project, as well as the interest and enthusiasm with which the Music Encoding Initiative community greeted Hughes' legacy dataset in the years after his passing. Our thanks also to the CANTUS community for its continuing support as we integrate our approaches to larger sets of chant data with those of other scholars represented on the platform.
NOTES
-
Correspondence can be addressed to: Dr. Kate Helsen, Don Wright Faculty of Music, The University of Western Ontario, Talbot College 210, London Ontario, N6A 3K7, kate.helsen@uwo.ca.
Return to Text -
'Close enough' is formalized mathematically by generating a cutoff value of cosine similarity beyond which we are statistically doubtful that two chants are truly related using a false discovery rate (FDR) approach.
Return to Text -
REAL FLATS
If there is a flat (notated as '<') in the manuscript:- if the chant starts with '<' then all 'b's in the melody are flattened (Hughes, p.176)
- otherwise, if the '<' does not start the chant, flatten all the subsequent b's after the '<' until:
- there is the end of a phrase shown with a rhyming word, notated with a semi-colon (';') in Hughes's notation.
- the current hexachord is clearly changed. That is, we look for a 'd' or an 'e' in the specific chant word to show a change in hexachord.
For instances of 'h-j-h' in modes 1, 2, 5, and 6:- if a 'd' directly precedes the 'h-j-h' (ie. d-h-j-h) the 'j' is flattened
- if the note 'k' precedes or succeeds the 'h-j-h' (ie. k-h-j-h or h-j-h-k) the 'j' is not flattened
- otherwise, we use an algorithm that gives each instance of the substring a score to try to determine if the substring is in a D or F hexachord:
- for h-j-h in modes 1,2
- If there's a k,l, or m in the same word as the h-j-h, +3 to the score
- If there's a k,l, or m in the word before or after the word with h-j-h, +2 to the score
- If there's a k,l, or m in the word 2 before or after the word with h-j-h, +1 to the score
- for h-j-h in modes 5,6
- If there's an m in the same word as the h-j-h, +3 to the score
- If there's an m in the word before or after the word with h-j-h, +2 to the score
- If there's an m in the word 2 before or after the word with h-j-h, +1 to the score
For instances of a Gallican cadence ('b-c-c') in modes 5 or 6 or a chant transposed to C we always flatten the 'b'
ASSOCIATED FLATS
For instances of 'ij' (modes 1, 2, 5 and 6):- if there is a flat 'ij' (implied or real) every 'j' in that word and after it is flattened until:
- the chant clearly changes hexachord (that is, until we see notes k or l in modes 1 and 2 or notes l or m in modes 5 or 6). With this we assume that modes 1 and 2 will be working in a 'd' hexachord and modes 5 and 6 in an 'f' hexachord
- we see a rhyme indicated in the Hughes's data (with a capital letter and a ';' at the end of the word)
- if there is an instance of 'h-ij-h' (mostly implies flats) flatten all instances of 'j' before the 'h-ij-h' until
- the chant clearly changes hexachord (that is, until we see notes k or l in modes 1 and 2 or notes l or m in modes 5 or 6). With this we assume that modes 1 and 2 will be working in a 'd' hexachord and modes 5 and 6 in an 'f' hexachord
- we see a rhyme indicated in the Hughes's data (with a capital letter and a ';' at the end of the word)
- For instances of 'yb' (all modes):
- anytime there is a 'yb' (implied or real) expand in both directions until we see a rhyme indicated in the Hughes's data (with a capital letter and a ';' at the end of the word)
- Dealing with duplicate words:
- we cross check duplicate words in the chant. If one has flats added to it during the process, the other is changed to the flattened version.
Return to Text
REFERENCES
- Ariza, Christopher (2005). The Xenakis Sieve as Object: A New Model and a Complete Implementation. Computer Music Journal 29, No. 2:40 - 60. https://doi.org/10.1162/0148926054094396
- Broze Y. and Daniel Shanahan (2013). Diachronic Changes in Jazz Harmony: A Cognitive Perspective. Music Perception: An Interdisciplinary Journal, Vol. 31, No. 1, 32-45. https://doi.org/10.1525/mp.2013.31.1.32
- Carvell, B. (1988). Notes on 'Una nota supra la'. Music from the Middle Ages Through the Twentieth Century. New York: Gordon and Breach Science Publishers.
- Claire, J. (1963). L'Évolution modale dans les recitatifs liturgiques. Revue gregorienne, 127-151.
- Claire, J. (1962). L'Évolution modale dans les repertoires liturgiques occidentaux. Revue gregorienne 40, 196-211, 229-245.
- Hankeln, R. (2008). Old and new in medieval chant. Finding methods of investigating chant in an unknown region. A Due. Musical Essays in Honour of John D. Bergsagel & Heinrich W. Schwab. Musikalische Aufsätze zu Ehren von John D. Bergsagel & Heinrich W. Schwab, Ole Kongsted, Niels Krabbe, Michael Kube and Morten Michelsen ed., 161-180.
- Hansen, F. E. (1979). The Grammar of Gregorian Tonality. (doctoral dissertation) The University of Michigan, Ann Arbor, USA.
- Helsen, K. (2008). The Great Responsories of the Divine Office: Aspects of Structure and Transmission. (doctoral dissertation) University of Regensburg, Regensburg, Germany.
- Hornby, E. (2002). Gregorian and Old Roman Eighth-mode Tracts: A Case Study in the Transmission of Western Chant. Abingdon-on-Thames: Routledge.
- Hornby, E. (2009). Medieval Liturgical Chant and Patristic Exegesis: Words and Music in the Second-Mode Tracts. Suffolk: Boydell Press.
- Hughes, A. (1994, 1996). The Late Medieval Liturgical Offices, 2 vols. Toronto: Pontifical Institute of Mediaeval Studies.
- Hughes, A. (2011). The Versified Office: Sources, poetry, and chants. Lions Bay, BC: The Institute of Medieval Music.
- Nowacki, E. (1980). Studies on the Office Antiphons of the Old Roman Manuscripts. 2 vols. (doctoral dissertation) Brandeis University, Waltham, Massachusetts, USA.
- Jeffery, P. (2001). The Study of Medieval Chant: Paths and Bridges, East and West. In Honor of Kenneth Levy. Suffolk: Boydell Press.
- Nylund, H. (1983). Syntactic Structures of North Indian Rāgas. The World of Music, Vol. 25, No. 2, 45 – 57.
- Sachs, C. (1943). The Rise of Music in the Ancient World East and West. New York: W. W. Norton & Co.
- Shumays, S.A. (2013). 'Maqam Analysis: A Primer'. Music Theory Spectrum Vol 35, No. 2, 135-168. https://doi.org/10.1525/mts.2013.35.2.235
- Van Deusen, N. (1972). An Historical and Stylistic Comparison of the Graduals of Gregorian and Old Roman Chant. (doctoral dissertation) Indiana University, Bloomington, USA.
- Zippe, S. (2001). Die Formel in den Gesängen des gregorianischen Mepropriums. Beiträge zur Gregorianik 32, 29–56.