INTRODUCTION
IN the last few decades, the study of rhythm and meter from a psychological perspective has given rise to a wide range of methodological approaches, from observational to computational and experimental studies. These investigations are not limited to issues of perception and cognition, but also explore various aspects of performance, such as motor processes, memorization, and expressive timing. In the experimental domain, the tapping paradigm has been especially favored. Sensorimotor synchronization (SMS) to music, such as moving one's head or tapping one's foot to the underlying pulse (or beat), is a widely observed spontaneous phenomenon and does not require musical training (for a comprehensive review, see Repp, 2005, and Repp & Su, 2013). This behavior has been theorized to result from entrainment, i.e., the process by which a listener's attentional energy attunes to the recurrence of regularly spaced events in auditory signals (Large & Jones, 1999). In this context, the perception of first-order periodicity (FOP) results from the recurrence of an interonset interval (IOI) between adjacent auditory events, while the perception of second-order periodicity (SOP) requires the listener to extract an isochronous IOI series from non-adjacent events. In actual music, rhythmic sequences usually contain both types of periodicities, in succession as well as simultaneously.
In SMS experiments, participants are asked to communicate their understanding of the beat by tapping with one or more fingers on a computer key, drumming pad, or keyboard. In general, studies have shown that participants are very good at synchronizing with a metronome (1:1 in-phase tapping) at rates ranging from about 150–200 msec to 1.8 sec, with the lower limit resulting from biomechanical rather than perceptual constraints (Repp, 2005). In selective tapping tasks (1:n synchronization), however, performance is better when groups of isochronous tones can be subdivided evenly (e.g., 1:8 and 1:9 as opposed to 1:5 and 1:7), with best performance being achieved when duple, rather than triple subdivision is possible (Repp, 2007). Furthermore, when asked to tap along or reproduce nonisochronous sequences, participants perform better when the temporal structure is characterized by integer rather than non-integer duration ratios, e.g., 2:1 and 3:1 as opposed to 3:2 or 4:3 (Franěk, Radil, & Indra, 1988; Repp, London, & Keller, 2005). Finally, in rhythmic sequences that involve syncopation (as measured by the number of beats that are not explicitly marked by an event onset), performance accuracy decreases as the degree of syncopation increases (Fitch & Rosenfeld, 2007).
While the tapping paradigm provides a useful window into listeners' perception of meter as manifested by beat induction, it is obviously not meant to represent the totality of metric experience. In actual music, there can be several different possible periodicities to attune to, and meter itself is conceptualized as a nested hierarchy of at least two pulse levels related to each other by simple ratios such as 2:1, 3:1, or 4:1 (e.g., Keller & Burnham, 2005, p. 630; Yeston, 1976). Even if focal attention tasks are used, that is, tasks in which participants are asked to tap at the next higher and/or lower pulse levels (e.g., Drake, Jones, & Baruch, 2000; Drake, Penel, & Bigand, 2000), metric perception as such is only witnessed indirectly. 2 The use of neuroscientific methods has opened new possibilities for the observation of temporal processing, but much work is still needed to clarify how different timing mechanisms (such as "beat-based" and "interval-based" mechanisms; see Repp & Su, 2013, pp. 431-441) interact with one another, and direct evidence for specifically metric entrainment, which would require simultaneous entrainment to different pulse levels, is still lacking (for a discussion of advances and challenges facing neuroscientific research on musical rhythm, see Grahn, 2009). Thus, in most psychological studies, meter is tied to tactus, that is, a comfortable pulse level whose rate falls within boundaries that are closely related to bodily rhythms such as heart rate and walking speed (≈ 67–200 beats per minute, which corresponds to IOIs of 300–900 msec; e.g., see Todd, Cousins, & Lee, 2007). Given the central role tapping studies have played in shaping our understanding of pulse (and meter) perception, and that, with a few notable exceptions (e.g., Drake, Penel, & Bigand, 2000; Martens, 2011; Snyder & Krumhansl, 2001; Toiviainen & Snyder, 2003; Vuust et al., 2011), most of the stimuli used in these studies are not from actual music, we might ask how widely applicable these findings are. 3
The present study explores the phenomenon of mensural determinacy in complex rhythmic sequences. Because most musical rhythms afford multiple possibilities in terms of underlying periodicity, this study proposes to measure the relative salience of an implied beat across participants independently of tapping profile (i.e., the specific structure exhibited by participants' inter-tap interval series). The implied beat of the source materials was determined by music analysis based on this author's knowledge of the composer's aesthetic goals and stylistic tendencies. Because of the difficulty of the task, only musicians participated in the experiment, and participants' passive and active exposure to the style represented by the source materials was used as a measure of style-specific expertise.
Mensural Determinacy
The concept of mensural determinacy is borrowed from Hasty's (1997) Meter as Rhythm. In Hasty's theory, mensural determinacy emerges from a durational event, which, upon completion, becomes imbued with projective potential, that is, specific temporal expectations related to the duration of future events. 4 It is important to note that for Hasty, a measure (as opposed to a "bar-measure") results from the perception of a determinate duration and its projective potential. In other words, meter does not require the realization, but only the setting-up of an expectation of temporal regularity. Although it might be tempting to make a categorical distinction between mensural determinacy and indeterminacy, in practice it is more fruitful to consider the relative salience of an underlying periodicity based on a predetermined set of variables. Beyond musical parameters, individual preferences for tactus also need to be considered. Thus, in assessing mensural determinacy, one may be concerned with the likelihood that a particular rhythmic sequence will give rise to beat percepts whose periods are closely related to one another across listeners. While questions of mensural determinacy could certainly be explored in the context of nonisochronous beats, for practical and stylistic reasons, the present study is limited to isochronous beats.
The proposed conceptual framework is particularly attractive for the exploration of beat perception in Western art music of the twentieth century. For one, despite the explicit use of time signatures, the temporal structure of many of these works is much more irregular than that exemplified by the musical practice that gave rise to this notational convention. Such irregularity often means that while it might be possible to identify one periodicity, it is much less likely to find two or more nested periodicities that are sustained for a significant amount of time, which is a requirement for one to address questions of metric hierarchy. Furthermore, when considering beat induction across listeners, a pulse finding paradigm that relies on spontaneous tapping and measures accuracy across participants for a single beat period is problematic. Even if a given temporal structure is highly regular, individual preferences for tempo are likely to give rise to several different tapping periods related by simple pulse ratios (e.g., Drake, Penel, & Bigand, 2000; Jones et al., 1995; Martens, 2011; Parncutt, 1994). For irregular rhythmic sequences, this issue is magnified as a higher degree of syncopation also means that there are fewer structural constraints on induced periodicity. In this context, a more flexible measure might prove useful. Because of its emphasis on the projection of an underlying periodicity that may or may not be confirmed by a subsequent auditory event, mensural determinacy is well suited to investigate questions of temporal expectation without having to deal with assumptions pertaining to metric hierarchy. In this context, performance accuracy measures can be used to compare the relative influence of a given beat period or phase on participants' tapping, regardless of tapping profile.
Another advantage offered by the concept of mensural determinacy is its implicit appeal to some form of communicative process. The large majority of experimental studies dealing with beat induction focus almost exclusively on the temporal features of stimuli, and the percepts they give rise to, without considering compositional strategies and aesthetic goals. In other words, the exploration of musical communication is mostly one-sided. An important exception to this practice is exemplified by performance studies, particularly microtiming analyses that address questions of both random and systematic deviations from a notated rhythmic structure from the dual perspective of expressed and perceived structure (although in this case, expressed structure is determined based on performance rather than compositional strategies). While mensural determinacy can be assessed from the perspective of the listener (with or without the explicit consideration of the role of the performer), it can as easily address questions of compositional intent. Emphasizing the process of communication that is at play between composers, performers, and listeners, and recognizing the importance of a shared musical language (understood as a style-specific set of tools for signification) encourages us to address not only questions of compositional and performance strategies, but also of familiarity, competency, and expertise.
Rhythmic Complexity
Defining and measuring complexity in the temporal domain is not an easy task, especially if one considers rhythm perception as well as production. 5 Rhythmic complexity is commonly operationalized following structural criteria that rest on some form of isochronicity. 6 One widespread approach to measure complexity is based on the specific IOI ratios exhibited by a given rhythmic sequence, with the identity ratio (1:1) judged to be the simplest, followed by simple integer ratios (2:1, 3:1, and 4:1), and non-integer ratios such as 3:2 or 4:3; an alternative formulation of this principle involves a contrast between small-sum and large-sum ratios (e.g., Carson, 2007). The preference for smaller integer ratios has been linked to cognitive limits involving working memory (Drake & Bertrand, 2003), and it would seem that the total duration of a rhythmic pattern also plays a role. For example, a rhythmic sequence characterized by a 6:5 duration ratio and a referent pulse unit of 250 msec (a total duration of 2.75 sec) might be conceived as "less complex" than a sequence characterized by a 3:2 duration ratio and a referent pulse unit of 900 msec (4.5 sec total duration), based on the higher demand placed on working memory by the latter. Finally, if the stimuli involve human performance, microtiming variations need to be taken into account (e.g., by applying some form of quantization), and in some cases, larger-sum and smaller-sum ratios can be assumed to be perceptually equivalent. For example, given a very short referent pulse unit, 32:21 might be judged to be equivalent to, rather than more complex than, 3:2.
When the hypothesized temporal structure involves two pulse levels related by simple integer ratios, as is the case with metric hierarchies based on the duple or triple grouping of isochronous beats, the resulting framework provides a convenient grid by which to measure relative complexity, an approach we might refer to as the "goodness-of-fit" model. Rhythmic sequences in which more event onsets (or intensity accents) coincide with the implied accentual pattern of the underlying structure are judged to be simpler (or less syncopated), and those with a lower number of coinciding onsets, more complex (e.g., Jones & Yee, 1997; Povel & Essens, 1985). Rhythmic sequences that can accommodate more than one framework are described as being "ambiguous," and the temporal structure that is judged to be the simplest or most "economical" (Povel, 1984) will be presented as the "preferred" structure. Furthermore, sequences that exhibit highly irregular accentual patterns are often deemed "a-metric," without attempting to measure their relative complexity. An alternative approach might be to count the number of operations that need to be applied in order to transform a given complex (irregular) sequence into a simpler (normative) one (e.g., Tanguiane, 1993); this approach has also been proposed to measure rhythmic similarity/dissimilarity (Toussaint, 2013, pp. 246-257). Similarly, Lempel and Ziv (1976) measure the complexity of a rhythmic sequence by counting the number of steps required to generate the sequence. Taking perceptual experience into consideration, studies that have tested the predictive reliability of different complexity measures generally agree that models based on an isochronous framework (i.e., "clock" models) are more consistent with participants' complexity judgments (Schmulevich and Povel, 2000; Vinke, 2010).
Still, defining rhythmic complexity mostly on structural criteria is problematic, even if the criteria are revealed to be consistent with findings from behavioral experiments. Experimental research has shown that rhythms that are more familiar to some listeners will appear less complex to these listeners than rhythms with which they are unfamiliar (Snyder, Hannon et al., 2006). For example, metrical structures that involve nonisochronous beats (e.g., Balkan music) are not necessarily detrimental to task performance for enculturated listeners, as attested by recent developmental and cross-cultural studies on meter perception (Hannon, Soley, & Ullal, 2012; Hannon & Trehub, 2005a; Hannon & Trehub, 2005b; Hannon, Vanden Bosch der Nederlanden, & Tichko, 2012). Based on these findings, we may speculate on the influence of culture-specific expertise on the cognitive processing of temporal structures (Iversen, Patel, & Ohgushi, 2008). For example, in a study that combined structural equation modeling and covariance analysis, Magill and Pressing (1997) were able to demonstrate that a cognitive clock model based on nonisochronous pulses provided a good fit for most of the polyrhythmic patterns performed by an expert master drummer from West Africa. More generally, musicians have been found to exhibit enhanced skills in rhythmic tasks, such as lower thresholds for detecting timing deviations (Rammsayer & Altenmüller, 2006; Jones et al., 1995), access to a larger number of pulse levels (Drake, Jones, & Baruch, 2000; Drake, Penel, & Bigand, 2000), and greater facility in finding and subdividing an implied beat (Jones & Yee, 1997; Palmer & Krumhansl, 1990). Furthermore, although they are more sensitive to timing deviations, musicians are also more resilient to timing irregularities in pulse attribution tasks (Madison & Merker, 2002). Finally, when asked to judge the complexity of rhythmic sequences, musically trained listeners tended to judge these rhythms as less complex than musically untrained listeners (Vinke, 2010). Thus, it would appear that despite the observed correlation between different models of complexity measures and perceptual findings, structural complexity cannot be easily equated with perceptual complexity, and that a specific rhythm might be experienced as being more or less complex depending on the cultural background and musical experience of a given listener.
These issues come to the fore when one considers the rhythmic sequences typically found in Western art music of the twentieth century, the repertoire selected for this study. Composers of that period are generally recognized for their predilection for breaking with tradition and experimenting with novel musical structures. In the rhythmic domain, composers have employed a wide range of techniques, such as asymmetrical and mixed meters (e.g., Béla Bartók and Igor Stravinsky), proto- and total-serialism (e.g., Olivier Messiaen and Pierre Boulez), polytempo (e.g., Conlon Nancarrow and György Ligeti), and stratification (e.g., Charles Ives and Elliott Carter). In particular, complex rhythmic structures that result from textural as well as temporal stratification, i.e., the layering of contrasting rhythmic strands—each of which may be associated with a different speed, characteristic duration pattern, and/or rhythmic process (e.g., accelerating and decelerating strands against one another)—present a special challenge to our understanding of how rhythm and meter relate to one another in perception and cognition. In this repertoire, one is often faced with a musical surface that exhibits very irregular rhythmic sequences that are nonetheless built upon a regular metric framework characterized by simple ratios. In some cases, the situation is made even more complicated by the presence of two such frameworks, or polymeter, and thus more than one set of nested periodicities, each of which might be only weakly represented in the musical surface (Poudrier & Repp, 2013). While the underlying framework might not be readily apparent to most listeners, style-specific expertise, which assumes a certain degree of familiarity with the composer's aesthetic strategies, might enhance a listener's ability to detect an implied beat.
For the purpose of the present study, a complex rhythmic sequence is defined as a series of IOIs that cannot be readily mapped on a metric grid that results from the interaction of two pulses related to one another by simple integer ratios. Following the proposed conceptual framework, the relative degree of complexity of the experimental stimuli is not measured a priori, but is considered a product of style-specific expertise that is expressed through mensural determinacy, as measured by listeners' spontaneous synchronization with an implied beat period and phase.
Previous Studies
Previous studies most relevant to the present research include research on auditory streaming and multipart rhythm, and pulse-finding studies whose stimuli were derived from actual music. Although there are an increasing number of empirical studies that use actual music as source materials, few of these studies feature rhythmic sequences comparable to those that result from the use of temporal stratification as a compositional technique. Nonetheless, studies that measured the influence of musical expertise on task performance are of special relevance.
In considering questions of beat perception in polyphonic textures, it is useful to think of auditory streaming as involving two distinct types of streaming, i.e., textural streaming (the extraction of a specific auditory sequence) and mensural streaming (the extraction of a specific underlying period or SOP). The seminal work on auditory streaming is Bregman's (1990) Auditory Scene Analysis. Although Bregman's findings are based on very simple auditory stimuli, his proposition that schema-based streaming might be important in the context of musical stimuli is suggestive. Schemas are generally associated with learned behavior. Musicians are especially skilled at using various forms of selective attention, for example tracking changes in an ensemble while performing their own part, and we might speculate that schema-based streaming of both types (textural and mensural) might play a role in pulse finding in actual music.
While most experimental research using stimuli derived from actual music is likely to involve SOP, there is only a small number of studies that have focused explicitly on the perception of SOP. One notable example is Carson (2007), who investigated SOP in non-metric contexts. Using newly composed materials with nonisochronous sequences that exhibited "dissonant" (large-sum) first-order ratios (e.g., 11:2:10:16), but "consonant" (small-sum) second-order ratios (e.g., 1:2) in a range of tempi, Carson found that participants were able to detect underlying periodicities (referred to as "pulsedness") under certain loudness and pitch streaming conditions, with loudness and pitch distance resulting in higher "pulse confidence" ratings. Research on rhythm perception using polyrhythms also offers some pointers on the influence of musical parameters. For example, in a study with polyrhythms combining two or three 2-, 3-, 4-, 5-, and 7-element pulse trains, Handel and his colleagues found that participants' choice of temporal structure varied based on the relative amplitude (loudness), frequency (pitch), and duration of the rhythmic events (Handel, 1984; Handel & Lawson, 1983; Handel & Oshinsky, 1981). At the slowest rate, participants tended to integrate events from superposed pulse trains ("cross-rhythms"), while faster rates yielded more isochronous tapping, with a preference for pulse trains of lower cardinality at the fastest rate. And while Handel and colleagues did not find an influence of musical experience, they did observe a reliable effect of individual preference on tapping profile ("cross-rhythms" vs. "meter rhythms"). Unfortunately, the relative influence of each pulse train on participants' tapping profiles was not measured.
Another strand of research has focused on attentional issues related to competing rhythmic patterns (Jones et al., 1995; Keller & Burnham, 2005). Keller and Burnham's (2005) study is of special interest because it was not limited to isochronous pulse streams but developed an approach whereby several rhythmic sequences with varying degrees of alignment or "metric compatibility" are combined. In the first experiment, participants had on average 11.5 years of experience playing an instrument, and performed in an ensemble regularly. As expected, when asked to memorize embedded rhythmic patterns (recognition memory paradigm), participants performed better when concurrent rhythmic materials provided a good metrical match. The second experiment tested only professional percussionists with extensive performance experience in symphony orchestras and ensembles specializing in contemporary music, and extended the procedure to include reproduction (dual-task paradigm). While the findings were consistent with those of the first experiment, the deficit in performance between matched and mis-matched meters was less pronounced, with nonmetrical stimuli still yielding the poorest performance. Thus, while these experiments provide more evidence that hierarchical structure facilitates the perception and production of simultaneous nonisochronous sequences, they also point to differences in performance based on the specific type of musical experience of its participants.
The three pulse-finding studies used as models for the experimental design of the present study (Drake, Penel, & Bigand, 2000; Snyder & Krumhansl, 2001; Toiviainen & Snyder, 2003) featured contrasting musical materials ranging from J. S. Bach to ragtime and Bartók. However refined in construction these pieces are, none of them even comes close to the type of rhythmic complexity encountered in the source materials used in the present study. Furthermore, although Drake and colleagues (2000) and Snyder and Krumhansl (2001) investigated the influence of musical training, musical training was defined in the most general terms. Participants' experience with the styles exemplified by the source materials was measured, but its influence on participants' performance was not assessed. Nonetheless, the findings point to some of the benefits of musical expertise as well as musical factors that may enhance the determinacy of a specific pulse. Drake and colleagues (2000) compared mechanical (with and without intensity accents) and expressive (performance by a concert pianist) versions of six musical excerpts of different styles and tempi (tempo range = 90–150 beats per minute or bpm). Overall, they found that both musical expertise and microtiming had an influence on participants' performance. In particular, not only did musicians (who had on average 7 years of musical training or instrumental playing) tend to attune to a slower pulse than nonmusicians (who had no formal musical training or experience playing an instrument), but their tapping period also corresponded more often with the theoretically correct meter (as determined by the authors based on an analysis of the notated score), suggesting that musicians had access to a more complete and stylistically valid mental representation of the meter. Also of note is the finding that the addition of intensity accents on downbeats induced nonmusicians to tap at a slower rate, in a manner similar to musicians. Finally, although synchronization was generally poorer with the expressive version, the presence of expressive timing reduced the range of tapping rates, which suggests that microtiming patterns can function as specific cues for beat induction.
Tapping studies that seek to investigate the influence of different musical parameters and use actual music as source materials are faced with the challenge of balancing experimental control and ecological validity. In two experiments with piano ragtime music, Snyder and Krumhansl (2001) presented their participants with eight ragtime excerpts (tempo range = 86–102 bpm) in four different versions with texture (full and right-hand only) and pitch information (varied-pitch and monotonic) as variables. While there was no significant difference based on pitch information, synchronization performance was poorer in the right-hand only version, a finding that was attributed to its higher degree of syncopation. Post-hoc autocorrelation analysis of the temporal structure of the two parts revealed that there were no significant peaks for event onsets in metrically strong positions in the right hand, while the left hand exhibited peaks at two, four, and eight sixteenth notes. In the first experiment, the researchers investigated the influence of musical experience (musically experienced participants' mean years playing music was 13 as compared with 3 for musically inexperienced participants). Contrary to the findings of Drake and colleagues (2000), there was no significant effect of musical experience on participants' performance. It is worth noting that the average reported familiarity with ragtime music (on a 7-point scale) ranged only from 2.2 to 3.9, and that it may be that the lack of style-specific expertise weakened the potential influence of musical experience on the task.
Toiviainen and Snyder (2003) investigated the musical features that support pulse finding by varying the amount of information (left-hand, right-hand, and whole) and metrical orientation (starting and ending on the first vs. third eighth-note beat of a 2/2 meter) in eight excerpts of eight bars each, taken from a mechanical performance of J. S. Bach's organ duetto for solo performer, BWV 805 (tempo = 75 bpm). Because of the difficulty of the task (suggested by the results of a pilot study), all participants were musically trained, with at least 8 years of experience playing an instrument or singing (M = 12.1), and a reported average familiarity of 4.5 and 1.7 on a 7-point scale with the music of J. S. Bach and the source materials, respectively. Findings pointed to a strong bias for tapping to the phase corresponding to the starting metrical position, as well as to a facilitation effect when the two parts were presented together. A post-hoc principal component analysis of four quantifiable musical variables (onsets at the eighth-note pulse level, melodic direction changes, syncopation at the half-note pulse level, and notes longer than an eighth note) revealed that a high degree of syncopation resulted in a less stable tapping performance.
As the findings from these few studies suggest, musical experience can give rise to significant differences in the performance of both production and perceptual rhythmic tasks. The use of actual music as source materials, while enhancing ecological validity, may also require participants to be musically experienced, thus limiting the researchers' ability to test the effect of musical experience on participants' performance. As the present study will show, such limitations can be avoided by using more specific measures of expertise.
THE PRESENT STUDY
The goal of the present study was to investigate beat induction in complex rhythmic sequences and the influence of style-specific expertise (SSE) on tapping performance. Mensural determinacy was measured across participants, taking into account both passive and active exposure to the style represented by the source materials. Two questions guided the experimental design: (1) what degree of mensural determinacy is afforded by rhythmic complexity, as exemplified by twentieth-century Western art music? And (2) what is the influence of compositional strategies, attentional strategies, and SSE on listeners' ability to synchronize with an underlying periodicity? Because of practical limitations, performance issues were not investigated.
Taking into account findings from cross-cultural and expertise studies that point to the importance of familiarity and musical training, it was hypothesized that specialized skills are more likely to manifest themselves in the relevant musical context. The source materials were chosen based on three criteria: (1) musical style; (2) temporal structure (a combination of surface complexity and underlying periodicity); and (3) texture. Apart from their characteristic surface complexity, works that exhibit stratification offer the distinct advantage of presenting at least two contrasting musical layers simultaneously, and thus were thought to afford a good balance between ecological validity and experimental control. By segregating the different layers, beat induction could be measured independently for at least two contrasting temporal structures. At the same time, the presence of two simultaneous layers allowed for an investigation of the interaction of the component temporal structures as well as of different attentional strategies (focal versus global attention).
Structural Features of Source Materials
| Note Value (SYMBOL) | IOI (SEC) | Rate (BPM) |
|---|---|---|
| Septuplet thirty-second | 0.119 | 504 |
| Triplet sixteenth | 0.139 | 432 |
| Quintuplet sixteenth | 0.167 | 360 |
| Sixteenth | 0.208 | 288 |
| Triplet eighth | 0.278 | 216 |
| Quintuplet eighth | 0.333 | 180 |
| Eighth | 0.417 | 144 |
| Triplet eighth + sixteenth | 0.486 | - |
| Dotted quintuplet eighth | 0.5 | 120 |
| Triplet quarter Eighth + triplet sixteenth | 0.556 | 108 |
| Dotted eighth | 0.625 | 96 |
| Quintuplet quarter | 0.667 | 90 |
| Eighth + triplet eighth | 0.694 | - |
| Quarter | 0.833 | 72 |
| Dotted quintuplet eighth + eighth | 0.917 | - |
| Triplet quarter + eighth | 0.972 | - |
| Quarter + sixteenth | 1.042 | - |
| Triplet half Quarter + triplet eighth | 1.111 | 54 |
| Dotted quarter | 1.25 | 48 |
| Quarter + triplet quarter Dotted quarter + triplet sixteenth | 1.389 | - |
| Double-dotted quarter | 1.458 | - |
| Dotted quarter + triplet eighth | 1.528 | - |
| Half | 1.667 | 36 |
| Triplet whole Half + triplet quarter | 2.222 | 27 |
| Dotted half | 2.5 | 24 |
| Whole | 3.333 | 18 |
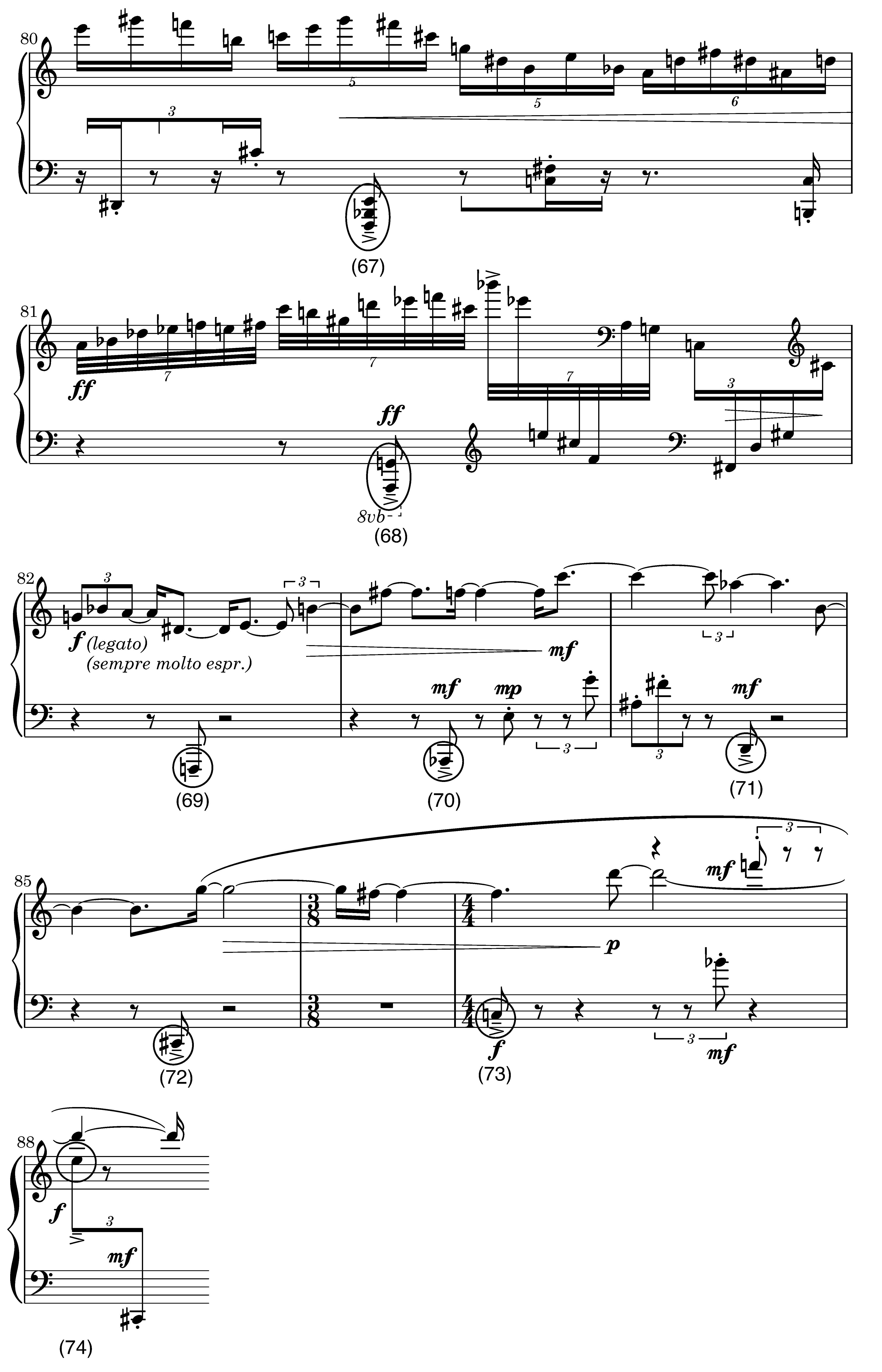
The source materials chosen for this experiment consisted of the molto espressivo section of Elliott Carter's 90+ for piano (1994), a work that is representative of textural and temporal stratification in twentieth-century Western art music. In particular, this excerpt provided the opportunity to investigate beat induction in two contrasting rhythmic sequences that are nonetheless based on a common referential periodicity, with the respective underlying quarter-note beats in anti-phase with one another (interleaved beats). The upper layer is characterized by various instances of FOP resulting from the irregular subdivision of an underlying duration pattern, while the lower layer is characterized by an irregular rhythmic sequence with a few instances of FOP, but explicit SOP.
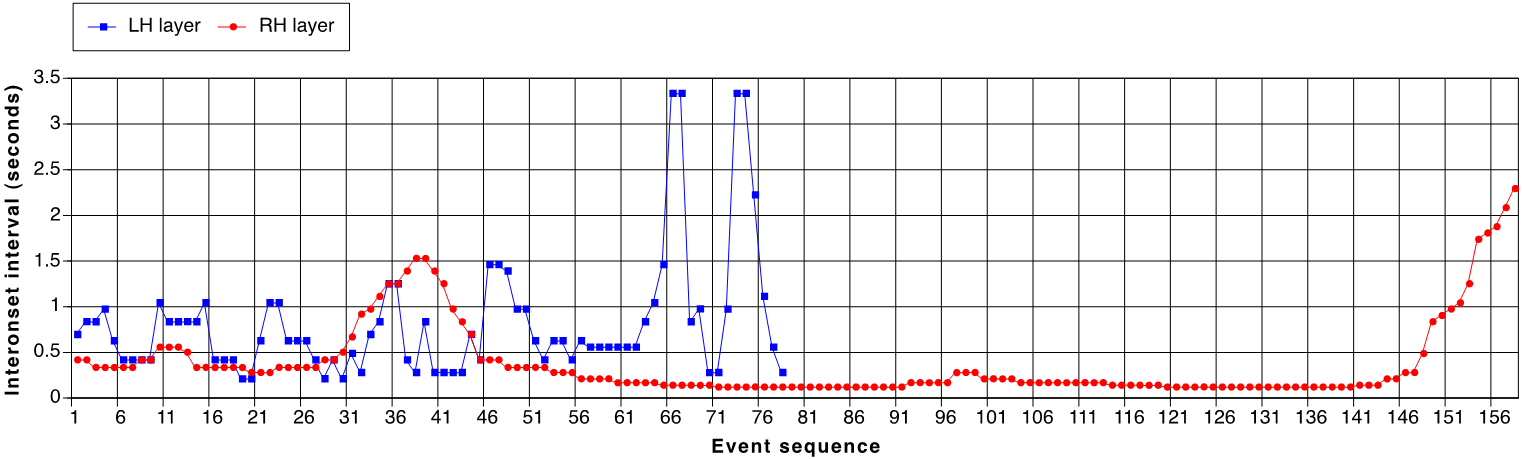
Fig. 1. Interonset interval (IOI) series for the left-hand (LH) and right-hand (RH) layers of Elliott Carter's 90+ for piano, m. 68, fourth eighth note, to m. 88, fifth sixteenth note. The two event sequences exhibit contrasting rhythmic profiles, with gradual tempo changes in the RH and an alternation of periodic and non-periodic events in the LH, with only eight first-order periodicities that correspond to the quarter-note beat (quarter = 72 bpm or 833 msec).
The excerpt extends from m. 68, fourth eighth note, to m. 88, fifth sixteenth note, inclusive; a reproduction of the entire excerpt is included as Appendix A and B. Figure 1 presents each of the two layers as an IOI series. In the original score, the passage is notated with a 4/4 time signature and a prescribed tempo of quarter note equal to 72 bpm; its mechanical performance lasts about one minute. The two component layers correspond roughly to the right and left hands of the pianist (designated RH and LH in Figure 1), although the two parts cross in register a few times. The right-hand layer consists of a mostly stepwise but sweeping melody built from subdivisions of an underlying 1:2 duration pattern; in notational value, these subdivisions range from septuplet sixteenth to triplet quarter notes. This temporal design suggests at least two nested pulse levels in a 3:1 ratio, that is, a quarter note at 72 bpm and a dotted-half note at 24 bpm, corresponding to chronometric durations of 0.833 and 2.5 sec, respectively. The left-hand layer consists of an accompaniment with regularly accented lower tones whose IOIs correspond to a SOP of 18 bpm (3.333 sec), the rate and duration associated with the whole note. These slow pulsations alternate with short staccato notes in a higher register, most of which are notated as triplet eighth and sixteenth notes, resulting in a highly irregular rhythmic sequence. The compound layer suggests measures of four quarter notes at 72 bpm, and this structure is explicitly presented only once toward the beginning of the passage (from m. 70, fourth eighth note, to m. 71, third eighth note). Table 1 presents the range of notational values used in both layers, with the corresponding IOIs (in msec) and tempi (in bpm).
The superposition of the two layers can thus be interpreted as resulting in an implied polymetric structure of 3/4 against 4/4 in which the quarter-note beats are interleaved due to an eighth note displacement (417 msec) of the beats of one layer in relation to those of the other layer. Although there are no coinciding beats, the two layers could be partially integrated at the eighth and sixteenth pulse levels.
Experimental Goals
The features of the source materials made it possible to explore the influence of a set of musical (within-subjects) variables on beat induction and mensural determinacy. The three specific questions that guided the experimental design were:
- Does style-specific expertise (passive and active exposure to Western twentieth-century music) influence participants' tapping performance?
- What is the relative degree of mensural determinacy of the implied quarter-note beat for each rhythmic layer, and how does it change when layers are combined?
- What is the influence of musical parameters (within-subjects) and participants' characteristics (between-subjects) on participants' ability to synchronize with the implied beat?
Because the population sampling method was convenient rather than random, the main analysis was limited to a relatively small set of within-subjects variables or "primary" musical parameters (global temporal structure, accent, and texture). However, the features of the source materials afforded an exploration of the influence of a number of "secondary" musical parameters (global pitch structure, articulation, contour, and register). Participants' characteristics also allowed for post-hoc exploration of the influence of a set of between-subjects variables (gender, formal musical training, main instrument, and piano skills). These findings are reported as possible avenues for future research.
METHODS
Participants and Between-Subjects Variables
Thirty participants (women = 13; men = 17), were recruited from a graduate program in music and from a semi-professional choir. The basic requirement was that participants be musically active and have received formal musical training equivalent to at least one year of undergraduate studies. Because the rhythmic sequences used in this experiment were relatively complex, it was thought that the task would be too difficult for nonmusicians. All participants except one were right-handed, and no participant reported hearing problems.
Prior to the experiment, participants completed a questionnaire on their musical training and activities, experience with twentieth-century music, and familiarity with the source materials. Six participants were amateur musicians and the remaining participants were music students and/or professional musicians; participants also identified themselves as primarily engaged in one of five areas of specialization, i.e., composition (2), ethnomusicology (1), musicology (5), theory (9), and performance (13), the latter including all amateurs, whose primary musical activity was choir singing. Prior knowledge of polyrhythm and/or polymeter was not a requirement; however, 19 participants reported having experience with performing polyrhythms and these participants were asked to provide some details about learning and performance strategies (not included in this report). Four participants reported no familiarity with polyrhythm or polymeter; the concepts were explained to them prior to the beginning of the experimental tasks. Only three participants knew about or had heard Carter's 90+ before, but none reported having performed or studied the piece extensively, and only two participants identified themselves as very familiar with the composer's music.
Participants varied widely in SSE, which was calculated in hours per week spent performing, analyzing, and/or listening to twentieth-century Western art music (M = 9.84, SD = 8.23). In addition to gender, three between-subjects variables were selected for exploratory analyses of the influence of specific aspects of musical training on participants' ability to extract a regular beat: formal musical training, main instrument, and piano skill level. Participants' formal musical training, as represented by degree, varied from the equivalent of one year of undergraduate studies to a completed PhD (no degree = 6, bachelor's = 5, master's = 18, and PhD = 1); this data was transformed into two groups: "no degree/bachelor's" (11) and "master's/PhD" (19). Participants' main instruments were combined into three roughly balanced groups based on register and/or sound production: "piano/percussion" (9), which included only one percussion player; "high melodic" (14), which included flute, alto/soprano voice, and clarinet; and "low melodic" (7), which included double bass, cello, and bass/tenor voice. Reported skill level at the main instrument ranged from beginner/intermediate (5) to advanced (15) and expert (10), but this information was not used for statistical analysis. Finally, participants also varied in their reported skill level at the piano: "none/beginner" (10), "intermediate" (11), and "advanced/expert" (9).
Manipulation of Independent Variables (Source Materials)
Each layer was transcribed using the notation software Finale 2006, converted into MIDI files, and manipulated using the sound editing software Cubase SX and samples from the Garritan Personal Orchestra VST. 7 All files were converted in .wav format and normalized to peak amplitude. The temporal structure of the notated score was preserved, but the excerpt was manipulated in various ways to allow for a comparative analysis of the influence of musical parameters on perceived temporal structure, for a total of 18 stimuli (see Table 2 for a descriptive list of the experimental stimuli; sound files for the stimuli can be accessed at http://hdl.handle.net/1811/85871):
- Texture: ten stimuli featured segregated layers (L vs. R) and eight stimuli presented the two layers simultaneously (L+R);
- Pitch (timbre and frequency): eight stimuli used the reverberated teak stick sample (indeterminate pitch) and ten stimuli used the reverberated Steinway piano sample (determinate pitch);
- Accent (attack velocity): notated accents in L were preserved in five and suppressed in seven stimuli; in R, accents were added to attacks coinciding with the implied quarter-note beat when it corresponded to an event onset in four stimuli; all accents were produced by increasing attack velocity based on the standard MIDI scale (flat velocity = 70, accented notes = 85–110);
- Articulation (duration): five of the ten stimuli with determinate pitch featured a reversal of articulation, from staccato (45% of quarter-note value) to legato (100%) and legato to staccato; tenuto accents were performed at 125% of the notated value, without changing the IOI;
- Contour and register: in two L stimuli, the contour was collapsed to a range of one octave by transposing pitch outliers down or up an octave; one L+R stimulus featured register reversal.
| Stimuli | Descriptive Labels* |
|---|---|
| BLOCK 1 (segregated layers, pitch off) | L-off |
| L-on | |
| R-off | |
| R-on | |
| BLOCK 2 (segregated layers, pitch on) | L-off.sta.asw.low |
| L-on.sta.col.low | |
| L-off.leg.asw.low | |
| R-off.leg.hig | |
| R-on.leg.hig | |
| R-off.sta.hig | |
| BLOCK 3 (combined layers, pitch off) | L-off + R-off |
| L-on + R-on | |
| L-on + R-off | |
| L-off + R-on | |
| BLOCK 4 (combined layers, pitch on) | L-on.sta.asw.low + R-off.leg.hig (C1) |
| L-off.leg.col.low + R-off.leg.hig (C2) | |
| L-off.leg.asw.low + R-off.sta.hig (C3) | |
| L-on.leg.asw.hig + R-off.sta.low (C4) |
*Legend for descriptive labels:
L = left-hand layer
R = right-hand layer
on = accents on
off = accents on
sta = staccato articulation
leg = legato articulation
asw = contour as written
col = collapsed contour
low = low register
hig = high register
All sound files included the entire excerpt, and the exact duration of the stimuli varied depending on whether one or both layers were present (L and L+R = 64.167 sec; R = 62.917 sec). Sound files were performed stereophonically. For the segregated layers conditions (L or R), each layer was piped through both channels equally; in the combined layers condition (L+R), stereo separation was created by panning one track 33% to the right and one track 33% to the left to avoid incidental noise. 8
The 18 stimuli were presented in four blocks of trials based on texture and pitch. Blocks 1 and 2 presented the segregated layers conditions (L vs. R), first with indeterminate pitch or pitch "off" (block 1), and then determinate pitch or pitch "on" (block 2). Blocks 3 and 4 presented the combined layers conditions (L+R), first with pitch off (block 3) and then pitch on (block 4). This design allowed for within- and across-block comparisons. Blocks 1 and 3 featured a balanced design, which allowed for hypothesis testing; the unbalanced design in blocks 2 and 4 only afforded exploratory analysis.
Apparatus and Procedure
The experiment took place in a private room in the music department. Participants were sitting at a desk and the principal investigator (this author) was sitting about 5 feet away on the left side of the desk. All sound files were placed on an interface controlled by a program created with Max/MSP and run with a MacBook 1.83 GHz Intel Core Duo. The sound files were played through standard quality headphones (SENTRY HO268) and participants were instructed to adjust the volume to a comfortable level. Participants controlled all manual operations and tapping was performed using the right arrow key on the computer keyboard.
Before beginning the experiment, participants signed a consent form and the principal investigator read an introductory statement about the experimental procedure. This was followed by a short practice session with a stimulus not included in the experiment. During the experiment, all instructions were given verbally and participants could ask for clarifications at any time as well as provide verbal comments in between listening and tapping tasks. For the listening-only part of the task, participants were instructed to move or not with the music as they would normally do. For the listening-and-tapping part of the task, participants were instructed to tap to the "underlying pulse or beat," which might involve not tapping at all if they felt there was no underlying pulse, or altering the speed or duration associated with the beat if they felt that it was altered, as it may occur in actual music.
In the first three blocks, participants heard each stimulus twice, first without tapping and then tapping along. 9 Although participants were instructed to first listen without tapping, many used this first listening as a "practice" session, trying out a given underlying pulse or beat by tapping on the desk, conducting with one or both hands, foot tapping, or a combination of these. For the last block, participants heard each sound file three times. After the first listening, they were asked to describe the texture. The main purpose of this first listening was to establish a common vocabulary that could then be used by the principal investigator to subsequently direct the participants' attention to each layer. For the second and third listenings, participants were instructed to focus successively on each one of the two contrasting layers and tap along "its main underlying pulse or beat." When a participant had identified more than two layers, which occurred only for L, the principal investigator instructed the participant to focus on the combination of identified layers that corresponded to L.
It was assumed that order of presentation could have an effect. Thus, presentation order was counterbalanced based on attended layer (blocks 1, 2, and 4), and was further varied systematically across all participants within layers, whenever applicable (blocks 2, 3, and 4). In addition, in blocks 1 and 3 (indeterminate pitch condition), unaccented stimuli were presented first to avoid a carry-over effect of accentual structure. It is assumed that this counterbalancing accounted for possible presentation order interactions with within-and between-subjects variables, but because of the unbalanced design in blocks 2 and 4, and the small number of cases for each presentation order group (up to 24 orderings in block 4), this assumption was tested only in the first block of trials (L-first vs. R-first).
Three types of data were gathered during the experiment: (1) participants' verbal comments were recorded using a SONY ICD-P320 digital voice recorder; (2) observations of participants' body movements during listening-only and listening-and-tapping were noted by the experimenter; and (3) tapping responses (timepoint series measured in milliseconds) were recorded by the computer program and saved as text files. All results presented here are derived from the tapping responses. The time-points text files were first imported into Excel and used to generate inter-tap interval (ITI) series for each tapping response. ITI series were then plotted as two-dimensional graphs and used for visualization of participants' tapping behavior. A computer script processed the data sets to identify taps that were synchronized with underlying pulses, and the criterion used for synchronized taps was ± 100 msec (e.g., Drake, Penel, & Bigand, 2000; Snyder & Krumhansl, 2001). 10 Cut-off points across stimuli were then normalized.
The experiment lasted between 1 and 2 hours depending on the number of verbal comments made by each participant. Participants were instructed to take a short break between the second and third blocks of trials.
Performance Measures and Analysis
Two basic types of performance measures were used for statistical analysis, i.e., tapping variability and phase synchronization. Variability measures in pulse-finding experiments are typically based on the standard deviation (SD) of an ITI series, i.e., the root-mean-square (RMS) deviation of the ITI values from their mean, and exclude false alarms. The measure used here was the coefficient of variability (CV), which is calculated by dividing the standard deviation by the mean ITI (SD/mean ITI), to allow for comparisons across tempi. To take into account local as well as global factors, all taps were included, whether or not they were actually synchronized with the implied beat (as determined by score analysis). Therefore, the observed CV performance in this study is not directly comparable with previous findings. The inclusion of all taps in the CV measure means that it is more sensitive to tapping fluctuations (yielding generally higher CV values than other tapping studies), which makes it possible to take into account participants' overall tapping behavior, but can also hamper statistical significance due to larger variance.
There were two different, but closely related, phase synchronization measures used in this study. Tapping synchronization, Tsyn, corresponds to the ratio of participants' synchronized taps, ST, to the total number of taps (Tsyn = STn/Tn); beat synchronization, Bsyn, corresponds to the ratio of participants' synchronized taps to the total number of available quarter-note beats, Q (Bsyn = STn/Qn). To differentiate between the interleaved quarter-note beats, phase synchronization measures are further designated by the labels L and R, whenever necessary; for example, TsynQL refers to tapping synchronization with the left-hand phase of the quarter-note beat and BsynQR refers to beat synchronization with the right-hand phase of the quarter-note beat. While both of these measures reflect the influence of the implied beat on participants' tapping behavior, Bsyn is a more objective measure of mensural determinacy as it is less sensitive to extraneous taps, including tapping with subdivisions of an implied beat. In most cases, results based on both types of synchronization will be reported.
It was hypothesized that SSE as represented by passive and active exposure to twentieth-century music would be reflected in participants' tapping behavior, with more exposure resulting in less tapping variability. To test this effect, a Pearson's correlation was applied using overall CV value and the number of weekly hours spent listening, performing, and/or analyzing twentieth-century music. Hypothesis-driven and exploratory statistical analyses were also conducted within and across blocks of trials. Analyses within and across blocks 1 and 3 tested the influence of the primary musical parameters (i.e., global temporal structure as represented by layer, accent, and texture) on participants' tapping behavior using CV, TsynQ, and BsynQ. Analyses within blocks 2 and 4 explored the influence of primary (layer and accent) as well as secondary (articulation, contour, and register) musical parameters. Analyses across blocks 1 and 2 as well as across blocks 3 and 4 explored the influence of global pitch structure (off vs. on), while those across blocks 2 and 4 explored the influence of texture (segregated vs. combined layers).
The two pulses used for statistical analysis correspond to the two different phases of the same beat period of 833 msec, i.e., the left- and right-hand phase of the quarter-note beat (designated as QL and QR, respectively). To assess the degree of mensural determinacy of each layer independently and in combination, phase discrimination analyses were also conducted both within and across blocks of trials using BsynQ only. In these analyses, phase dominance (QL vs. QR) was determined based on statistically significant differences in participants' synchronization performance to the L- and R-phase of the quarter-note beat (BsynQL or BsynQR); lack of statistical significance was interpreted as representing phase ambiguity (QA). In the context of this experiment, phase dominance is understood as a manifestation of mensural determinacy whether layers are presented independently or in combination. On the other hand, phase ambiguity in segregated layers indicates a low degree of mensural determinacy; in combined layers, a lack of statistically significant difference between the two phases of the quarter-note beat may result from an integrated percept which may or may not be mensurally determinate, depending on whether the tapping phase is stable or not (phase shifting).
Repeated measures univariate analyses of variance (ANOVA) were used within and across blocks to assess significant main effects and interactions of within- and between-subjects variables, and paired-samples t tests were used to determine significant differences between sets of trials, whenever necessary. The significance level for all statistical analyses was based on a 95% confidence interval (p < .05), and trends are reported based on a 90% confidence interval (p < .10); significance levels are given in full whenever possible. Missing cases were excluded from each separate analysis and the number of valid responses is provided for each result. Pairwise comparisons and post-hoc tests were performed using a Bonferroni adjustment for multiple comparisons, and Greenhouse-Geisser adjustments for sphericity were applied whenever necessary. The choice of adjustments was guided by the repeated measures design, with a preference for a more conservative adjustment because of the relatively small sample size.
Finally, post-hoc exploratory analyses of between-subjects variables (i.e., gender, formal musical training, main instrument, and piano skill level) were conducted within each block only, using all three measures (CV, TsynQ, and BsynQ). Given that the sample was convenient rather than random, it should be noted that generalizations are applicable only for the population represented by the sample, i.e., graduate music students, amateur musicians, and professional musicians with at least one year of formal musical training who are actively engaged in musical activities (including performance, analysis, and composition).
RESULTS
Overall results will be reported first, followed by results for primary (blocks 1 and 3) and secondary (blocks 2 and 4) musical parameters, including phase discrimination (all blocks). The exploratory analyses of between-subjects variables (all blocks) will be presented at the end. Specific manipulations performed on the source materials will be described as needed to facilitate interpretation of the results.
Overall Tapping Performance and Influence of Style-Specific Expertise
Table 3 presents descriptive statistics for the experiment overall, including tapping variability (CV), and tapping and beat synchronization (TsynQ and BsynQ) for each block of trials. CV varied widely across participants, with individual participants' means for the whole experiment ranging from 0.088 to 0.880 (M = 0.379, SE = 0.034). Mean synchronization percentages were consistently low overall, but exhibited a high degree of variance across participants. Within blocks, individual participants' TsynQ performance ranged from 15.5 to 70.8%, while BsynQ performance ranged from 5.7 to 70.5%. The observed discrepancies between these two synchronization measures suggest that a number of participants might have been tapping sporadically (i.e., heard some passages as not having a regular underlying periodicity), at slower or faster consonant rates (e.g., half- or eighth-note level), or partially consonant rates (e.g., dotted quarter-note level), with TsynQ < BsynQ suggesting a faster tapping rate, and TsynQ > BsynQ suggesting slower and/or intermittent tapping. Although individual participants achieved the highest tapping synchronization percentages in block 1 (segregated layers with pitch off), this is also where the largest variance across participants (within each synchronization measure) was observed.
| BLOCK | CV | TsynQ | BsynQ | ||||||
|---|---|---|---|---|---|---|---|---|---|
| MEAN | ST. DEV. | RANGE | MEAN (%) | ST. DEV. | RANGE | MEAN (%) | ST. DEV. | RANGE | |
| BLOCK 1 (N = 29) | .412 | .195 | .069–.726 | 31.9 | 11.5 | 15.5–70.8 | 24.2 | 14.3 | 5.7–70.5 |
| BLOCK 2 (N = 27) | .357 | .196 | .083–.866 | 29.1 | 8.7 | 18.7–52.2 | 20.5 | 11.8 | 6.3–52.7 |
| BLOCK 3 (N = 29) | .367 | .263 | .054–1.006 | 26.9 | 4.0 | 20.8–37.9 | 25.5 | 10.8 | 7.5–55.8 |
| BLOCK 4 (N = 27) | .384 | .208 | .058–.761 | 26.8 | 4.3 | 20.5–38.0 | 22.4 | 10.1 | 6.1–41.1 |
As shown in Figure 2, there was a significant negative correlation between CV and style-specific expertise, r(26) = -.406, p = .032. Participants who had more weekly exposure to twentieth-century music exhibited more stable tapping behavior than participants who had less weekly exposure. However, there appears to have been a number of outliers as well as a ceiling effect at about 10 hours per week, which suggests that there might be other between-subjects variables that influenced participants' tapping performance. 11
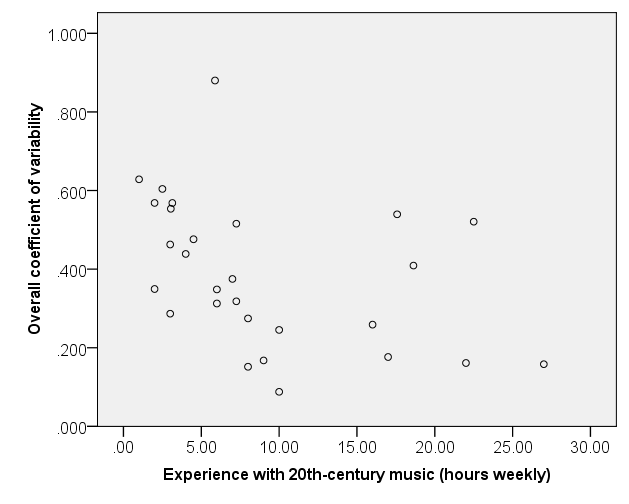
Fig. 2. Participants' overall coefficient of variability (CV) against style-specific expertise (SSE), measured in hours weekly devoted to musical activities with twentieth-century music. The distribution of participants' individual overall CV performance is consistent with the hypothesis that SSE contributes to more regular tapping.
Primary Musical Parameters
EFFECT OF ORDER, LAYER, AND ACCENT (BLOCK 1)
Block 1 presented each layer separately (L/R), first without and then with intensity accents (off vs. on), controlling for pitch (off). The factorial design allowed for statistical analysis of the effect and interaction of global temporal structure and accent on tapping behavior, as well as for an assessment of the mensural determinacy of the quarter-note beat independent of global pitch structure.
| VARIABLES | CONDITIONS | CV | TsynQ | BsynQ | |||
|---|---|---|---|---|---|---|---|
| MEAN | MEAN DIF. (L/OFF – R/ON) | MEAN (%) | MEAN DIF. (L/OFF – R/ON) | MEAN (%) | MEAN DIF. (L/OFF – R/ON) | ||
| Order | L-first | .353 | -.122 | 37.7 | 12.2* | 29.1 | 10.2 |
| R-first | .475 | 25.6 | 18.9 | ||||
| Layer | L | .302 | -.219* | 35.4 | 7.2* | 28.7 | 9.1* |
| R | .521 | 28.3 | 19.6 | ||||
| Accent | off | .413 | -.003 | 28.2 | -7.3* | 21.7 | -4.9* |
| on | .410 | 35.5 | 26.6 | ||||
Note: * = p < .05
The order of presentation of stimuli in block 1 was counterbalanced between layers (L-first, N = 15; R-first, N = 14) based on the assumption that order would have an effect. A 2 × 2 × 2 preliminary univariate repeated measures ANOVA was performed with order (L-first/R-first), layer (L/R), and accent (off/on) as within-subjects variables (see Table 4). Order had a significant main effect on TsynQ, F(1, 27) = 11.004, p = .003. Participants who heard and tapped in the L-first condition synchronized their tapping significantly more with the quarter-note beat of both layers than those who performed in the R-first condition. Participants who tapped in the L-first condition also exhibited less variable tapping and synchronized with a higher number of quarter-note beats, but these differences fell short of significance, F(1, 27) = 3.049, p = .092, and F(1, 27) = 4.040, p = .055. There was no significant interaction of order with either layer or accent, so this variable was not included in subsequent analyses. 12
A series of univariate repeated measures ANOVAs was conducted with layer (L/R) and accent (off/on). It was found that layer had a significant main effect on all three dependent variables, i.e., CV, F(1, 28) = 25.130, p < .001, TsynQ, F(1, 28) = 6.719, p = .015, and BsynQ, F(1, 28) = 13.279, p = .001. Participants' tapping behavior was significantly less variable when tapping to L than R. Participants' synchronization percentages were also significantly higher for QL than QR. In contrast, accent had a significant main effect only on synchronization, TsynQ, F(1, 28) = 10.631, p = .003, and BsynQ, F(1, 28) = 5.485, p = .027. A significantly higher percentage of participants' taps were synchronized with the quarter-note beat when accents were on than when accents were off (TsynQ), and these synchronized taps also corresponded to a significantly higher percentage of quarter-note beats (BsynQ). Finally, there was a trend toward a significant interaction of layer and accent for CV, F(1, 28) = 3.969, p = .056, suggesting that the effect of accent on tapping variability might not be independent from global temporal structure, with participants' tapping to L-on being less variable than L-off and participants' tapping to R-on being more variable than R-off.
| BLOCK 1 (PITCH OFF) | BsynQL vs. BsynQR (MEAN %) | Significance (2-TAILED) | Phase Profile | |
|---|---|---|---|---|
| LAYER (L/R) | ACCENT (OFF/ON) | |||
| L | off | 26.5 > 15.5* | t(29) = 2.706, p = .011 | QL |
| L | on | 31.2 > 11.4* | t(29) = 3.632, p = .001 | QL |
| R | off | 16.9 < 17.3 | t(29) = 0.224, p = .825 | QA |
| R | on | 11.6 < 21.6* | t(28) = 4.658, p < .001 | QR |
Note: * = p < .05
Table 5 presents the results of the phase discrimination analysis (paired-samples t tests) for each layer (L/R) and accent (off/on) condition in block 1. A phase profile for each condition has been assigned based on phase dominance at the quarter-note beat level. Participants' tapping to L was consistent with an interpretation of the quarter-note beat as being mensurally determinate in both accent conditions, with mean differences of 11.0% (L-off) and 19.8% (L-on) in favor of L-phase. In contrast, phase dominance was observed only in participants' tapping to R-on, with a mean difference of 10.0% in favor of QR; participants' tapping with R-off was characterized by phase ambiguity (QA). These results are consistent with participants' higher synchronization performance in the L- than in the R-layer. Furthermore, the resulting phase profiles offer a possible explanation for the variegated effect of accents within each layer condition. Given that participants' tapping was less variable in the R-off than the R-on condition, it is possible that the SOP inferred from the accent structure suggested by the dynamic accents that were added to the source materials conflicted with the perceived pulse, and induced participants to change tapping period more frequently.
EFFECT OF LAYER-SPECIFIC ACCENTUATION (BLOCK 3)
Block 3 featured combined layers (L+R), controlling for pitch (off). Accentuation was manipulated in each layer independent of the other (L-accent off/on, R-accent off/on), resulting in a 2 × 2 factorial design. Indeterminate pitch afforded minimal potential for textural streaming, promoting global attention and integration of the competing temporal sequences. It was hypothesized that the presence of layer-specific accentuation would promote mensural streaming in favor of the accented layer. The four different combinations of accentuation allowed for the testing of the effect of accent on beat induction in combined layers (within-block analysis) as well as of the influence of the competing temporal sequence on the mensural determinacy of each of the two layers (across-block analysis).
In order to determine the effect of layer-specific accentuation, a series of univariate ANOVAs with L-accent and R-accent as within-subjects variables was conducted. A significant main effect of R-accent was observed (see Table 6). As expected, participants' synchronization to QR was significantly higher in the R-on than R-off condition, F(1, 28) = 47.977, p < .001, and F(1, 28) = 54.934, p < .001. Additionally, a lower proportion of participants' taps was synchronized with QL in the R-on than the R-off condition, F(1, 28) = 6.442, p = .017. There was no significant effect of R-accent on CV and BsynQL. Although there was no main effect of L-accent, there was a significant interaction of L-accent and R-accent, F(1, 28) = 5.659, p = .024, and F(1, 28) = 4.858, p = .036.
| DEPENDENT VARIABLES | L-ACCENT | R-ACCENT | |||
|---|---|---|---|---|---|
| OFF | ON | OFF | ON | ||
| CV | MEAN | .371 | .362 | .368 | .366 |
| MEAN DIF. (OFF – ON) | .009 | .002 | |||
| TsynQL | MEAN (%) | 22.7 | 22.4 | 26.5 | 18.7 |
| MEAN DIF. (OFF – ON) | 0.3 | 7.8* | |||
| TsynQR | MEAN (%) | 30.8 | 31.5 | 20.6 | 41.7 |
| MEAN DIF. (OFF – ON) | -0.7 | -21.1* | |||
| BsynQL | MEAN (%) | 23.1 | 20.4 | 23.0 | 20.5 |
| MEAN DIF. (OFF – ON) | 2.7 | 2.5 | |||
| BsynQR | MEAN (%) | 29.8 | 28.7 | 18.5 | 40.0 |
| MEAN DIF. (OFF – ON) | 1.1 | -21.5* | |||
Note: * = p < .05
Table 7 presents the results from the phase discrimination analysis (paired-samples t tests) for each condition within block 3. To facilitate interpretation, the resulting phase profile for each combined layers condition is preceded by the corresponding segregated layers' phase profiles (block 1). As can be observed from this phase profile summary, the superposition of the segregated conditions is not a simple addition. Instead, the integration of the two segregated layers appears to promote R-phase dominance. Furthermore, the quarter-note beat was perceived as mensurally determinate in only two conditions, both of which involved R-on (with L-off/on). This finding is consistent with the observed main effect of R-accent. Furthermore, R-off also appears to have interfered with L-phase dominance and promoted phase ambiguity, regardless of L-accent condition. The trend toward significance in favor of QL when R-off was combined with L-on suggests that this effect might have been somewhat mitigated by the presence of accents in L.
| BLOCK 3 (PITCH OFF) | BsynQL vs. BsynQR (MEAN %) | Significance (2-TAILED) | Phase Profile Summary (L + R) | |
|---|---|---|---|---|
| L-ACCENT | R-ACCENT | |||
| off | off | 22.4 > 21.2 | t(29) = 1.120, p = .272 | (QL + QA) → QA |
| off | on | 23.3 < 37.9* | t(28) = 2.665, p = .013 | (QL + QR) → QR |
| on | off | 23.1 > 15.3 | t(28) = 1.918, p = .065 | (QL + QA) → QA |
| on | on | 17.3 < 41.9* | t(29) = 5.817, p < .001 | (QL + QR) → QR |
Note: * = p < .05
EFFECT OF TEXTURE (BLOCK 1 VS. BLOCK 3)
The effect of texture (segregated vs. combined layers), inferred from the phase profile summary in block 3, was tested by conducting a series of paired-samples t tests across blocks 1 and 3 using all dependent measures. A significantly higher percentage of participants' taps (Tsyn) were synchronized with QL when L was presented alone than when it was combined with R, regardless of accent condition in both layers (see Table 8a). On the other hand, a significantly higher percentage of participants' taps were synchronized with QR only when R-on was combined with L-on; there was also a trend toward significance in the same direction when R-on was combined with L-off as well as a trend in the opposite direction for R-off combined with L-on (see Table 8b). Participants also synchronized with a significantly lower percentage of QL when L-on was combined with R-on than when it was presented alone (Bsyn); the difference between the segregated L-on and its combined version with R-off, however, fell short of significance (see Table 8a). In contrast, participants synchronized with a significantly higher percentage of QR when R-on was combined with L, regardless of accent condition (see Table 8b). These results confirm that interference occurred only for synchronization with QL, and most significantly when both layers were accented. Furthermore, when considering the results of both the phase discrimination and phase synchronization analyses, it would seem that when confronted with interleaved accents, and thus two possible phases of a quarter-note beat, participants were more likely to pick QR over QL rather than synchronizing at the faster consonant period afforded by the eighth-note beat.
| BLOCK 1 (PITCH OFF) | BLOCK 3 (PITCH OFF) | TsynQL B1 VS. B3 (MEAN %) | Significance (2-TAILED) | BsynQL B1 VS. B3 (MEAN %) | Significance (2-TAILED) |
|---|---|---|---|---|---|
| L-ACCENT | R-ACCENT | ||||
| off | off | 33.0 > 24.6* | t(29) = 2.531, p = .017 | 26.5 > 22.4 | t(29) = 1.133, p = .267 |
| on | 33.8 > 20.8* | t(28) = 4.276, p < .001 | 27.3 > 23.3 | t(28) = 1.130, p = .268 | |
| on | off | 38.1 > 28.3* | t(28) = 2.238, p = .033 | 32.1 > 23.1 | t(28) = 1.997, p = .056 |
| on | 37.9 > 16.3* | t(29) = 4.595, p < .001 | 31.2 > 17.3* | t(29) = 2.652, p = .013 |
Note: * = p < .05
| BLOCK 1 (PITCH OFF) | BLOCK 3 (PITCH OFF) | TsynQR B1 VS. B3 (MEAN %) | Significance (2-TAILED) | BsynQR B1 VS. B3 (MEAN %) | Significance (2-TAILED) |
|---|---|---|---|---|---|
| R-ACCENT | L-ACCENT | ||||
| off | off | 24.0 > 22.7 | t(29) = 1.012, p = .320 | 17.3 < 21.2 | t(29) = 1.470, p = .152 |
| on | 24.2 > 18.8 | t(28) = 2.009, p = .054 | 17.8 > 15.3 | t(28) = 0.927, p = .362 | |
| on | off | 31.8 < 39.8 | t(27) = 1.913, p = .066 | 21.5 < 37.4* | t(27) = 3.471, p = .002 |
| on | 32.5 < 44.8* | t(28) = 4.011, p < .001 | 21.6 < 40.2* | t(28) = 6.533, p < .001 |
Note: * = p < .05
Finally, participants' tapping was more stable when R-on was combined with L, regardless of L-accent (.364 and .401 as compared with .554 and .564 for R-on alone), t(27) = 3.475, p = .002 (L-off), and t(28) = 2.881, p = .008 (L-on). There was no significant difference in CV across blocks 1 and 3 for any of the other conditions, although there was a trend toward more stable tapping for the segregated L-on condition than its combined version with R-on (.249 as compared with .388), t(29) = 1.956, p = .060.
Exploratory Analysis of Secondary Musical Parameters
EFFECT OF LAYER, ARTICULATION, STREAMING, AND ACCENT (BLOCK 2)
Block 2 presented the segregated layers conditions with pitch on. In addition to different accent conditions, the use of determinate pitch and piano timbre allowed for the manipulation of articulation and contour. Because of the increased number of parameters and the necessary limitations of a single experimental session, these variables were not fully balanced within the block, but still allowed for an exploratory analysis of the influence of several parameters on participants' tapping behavior.
A 2 × 2 univariate ANOVA used four of the six trials (L-off.sta.asw.low, L-off.leg.asw.low, R-off.leg.hig, and R-off.sta.hig; refer back to Table 2 for more details) to test the effect of layer (L/R) and articulation (staccato/legato), controlling for accent (off). Layer had a significant main effect on all dependent variables, except BsynQ, which only approached significance, F(1, 27) = 3.936, p = .058. Participants' tapping was significantly more stable with L (.288) than with R (.461), F(1, 27) = 17.904, p < .001. Participants' tapping was also synchronized significantly more often with QL (32.7%) than QR (23.3%), F(1, 27) = 8.234, p = .008. Since there was no main effect of articulation and no significant interaction of layer and articulation, these results replicate the findings in block 1.
The second exploratory analysis examined the relative influence of registral and accentual streaming in L, controlling for articulation (staccato). The registral distribution of events in this layer features isolated lower-register events, resulting in large leaps and a range of more than one octave, which suggests the presence of two interleaved layers (refer to Appendix A and B). It has been shown that one possible effect of registral streaming on participants' tapping is lower rates of successful synchronization (e.g., Jones et al., 1995). However, the lower-register events in this layer are accented and articulate a consonant SOP that corresponds to a notated whole-note beat. In this context, accentual streaming might serve to enhance mensural determinacy, and thus mitigate the detrimental effect of registral streaming. A paired-samples t test found no significant difference between L-on with collapsed contour (L-on.sta.col.low) and L-off as written (L-off.sta.asw.low) for any of the dependent measures. These results suggest that registral and accentual streaming had a similar effect on participants' synchronization to an underlying pulse. 13
Since there was no main effect of articulation within layers, each of the two sets of data pertaining to the accents-off conditions were combined, resulting in one set for each layer condition (L-off.sta/leg.asw.low and R-off.sta/leg.hig), which made it possible to explore the effect of accent across layer conditions. A 2 × 2 univariate ANOVA was conducted with layer (L/R) and accent (off/on) as within-subjects variables. As previously observed, there was a significant main effect of layer, which resulted in significantly more stable tapping (.264 as compared with .433), F(1, 26) = 18.206, p = .000, and higher synchronization with QL (33.6 and 24.7% for TsynQL and BsynQL, respectively, as compared with 25.5 and 17.4% for TsynQR and BsynQR), F(1, 26) = 5.172, p = .031, and F(1, 26) = 8.176, p = .008. There was also a significant main effect of accent on tapping variability and synchronization. Participants synchronized with a larger number of quarter-note beats (BsynQ) in the accented (22.6%) than the unaccented condition (19.5%), F(1, 26) = 6.730, p = .015. In contrast to block 1, however, participants tapping was also significantly more stable in the accents-on (.323) than the accents-off (.374) condition, F(1, 26) = 5.602, p = .026. The mean difference for TsynQ was in the same direction (30.7% for accents on as compared with 28.4% for accents off), but fell short of significance, F(1, 26) = 3.758, p = .063. Also in contrast to block 1, there was no significant interaction of layer and accent, which suggests a regularizing effect of the global pitch structure on participants' tapping period.
| BLOCK 2 (PITCH ON) | BsynQL vs. BsynQR (MEAN %) | Significance (2-TAILED) | Phase Profile | |||
|---|---|---|---|---|---|---|
| LAYER (L/R) | ACCENT (OFF/ON) | ARTICULATION (STA/LEG) | CONTOUR (ASW/COL) | |||
| L | off | staccato | as written | 23.0 > 11.5* | t(29) = 3.032, p = .005 | QL |
| L | off | legato | as written | 21.0 > 10.3* | t(29) = 3.148, p = .004 | QL |
| L | on | staccato | collapsed | 28.1 > 12.4* | t(28) = 3.459, p = .002 | QL |
| R | off | staccato | - | 20.1 > 19.0 | t(29) = 0.684, p = .499 | QA |
| R | off | legato | - | 17.0 > 16.1 | t(27) = 0.848, p = .404 | QA |
| R | on | legato | - | 16.6 < 17.3 | t(28) = 0.631, p = .533 | QA |
Note: * = p < .05
Table 9 presents the results from the phase discrimination analysis (paired-samples t tests) for each condition within block 2. Mean differences between L- and R-phase were significant only in three out of the six conditions, all of which resulted in L-phase dominance when tapping to L, with mean differences ranging from 10.7% (L-off.leg.asw.low) to 15.7% (L-on.sta.col.low). The results for L are consistent with the findings in block 1, where participants' tapping to L resulted in L-phase dominance regardless of accent condition. In contrast to block 1, however, the R-phase of the quarter-note beat was not perceived as mensurally determinate (QA) even when accents were on, with mean differences ranging from only 0.7% (R-on.leg.hig) to 1.1% (R-off.sta.hig).
EFFECT OF PITCH (BLOCK 1 VS. BLOCK 2)
The global effect of pitch on tapping variability and phase synchronization was further explored by conducting two analyses across blocks 1 and 2, each of which controlled for a different accent condition. The first consisted of a univariate ANOVA with layer (L/R) and pitch (off/on) as within-subjects variables, controlling for accent (off); this analysis used six out of the ten conditions, including the two combined sets from block 2 (L-off, R-off, L-off.sta/leg.asw.low, and R-off.sta/leg.hig). 14 As expected, there was a main effect of layer in favor of L on all dependent variables, with participants' tapping being more stable with L (.317) than R (.459), F(1, 27) = 14.691, p = .001, and participants achieving significantly higher synchronization to QL than QR (32.2 and 22.8% as compared with 23.8 and 17.1% for TsynQ and BsynQ, respectively), F(1, 27) = 16.965, p = .000, and F(1, 27) = 10.273, p = .003. However, there was no significant main effect of pitch, and no significant interaction of layer and pitch.
The second analysis consisted of a series of paired-samples t tests using the remaining four conditions with pitch (off/on) as within-subjects variable, controlling for accent (on). 15 While there was no significant difference between the two L conditions (L-on vs. L-on.sta.col.low), there was a main effect of pitch on tapping variability for the two R conditions (R-on vs. R-on.leg.hig), with participants' tapping being more stable when pitch was on (.412) than off (.556), t(27) = 3.356, p = .002. There was no effect of pitch on synchronization performance. These results suggest that the potential regularizing effect of the global pitch structure on participants' tapping period might not be independent of temporal structure as represented by layer.
| DEPENDENT VARIABLE | Block 1 vs. Block 2 (MEAN %) | Significance (2-TAILED) |
|---|---|---|
| TsynQR | 31.8 > 26.8 | t(27) = 1.635, p = .114 |
| BsynQR | 21.5 > 17.2 | t(27) = 1.695, p = .102 |
| TsynQL | 16.0 < 23.9 | t(27) = 4.317, p < .001* |
| BsynQL | 11.9 < 16.3 | t(27) = 2.972, p = .006* |
Note: * = p < .05
The lack of a significant main effect or interaction of global pitch structure makes the finding of a different phase profile from QR to QA for R-on in block 2 difficult to explain, as pitch is the only difference between the two conditions. However, it is important to note that the exploratory analyses across blocks 1 and 2 involve a comparison of synchronization measures pertaining to the downbeat phases of L and R rather than downbeat and upbeat phases within L and R; it might be the case that the change in phase profile for R-on is related to participants' synchronization to the upbeat phase of R (i.e., QL). To test this possibility, a phase synchronization analysis (paired-samples t tests) was conducted across blocks 1 and 2 for the two R conditions (R-on vs. R-on.leg.hig). As expected, there was no significant difference in downbeat synchronization (QR) for either of the two synchronization measures (see Table 10). On the other hand, there was a significant difference in upbeat phase synchronization across blocks 1 and 2. Participants synchronized significantly more with QL when pitch was on than when pitch was off for both synchronization measures. These results suggest that when tapping with R-on.leg.hig, participants adopted a faster consonant tapping rate (e.g., eighth note level), which resulted in ambiguous phase synchronization.
EFFECT OF ATTENDED LAYER AND REGISTER (BLOCK 4)
Block 4 presented combined layers conditions with pitch on, which afforded focal attending. Within each condition, the manipulation of musical parameters was similar to that of block 2, i.e., there were variations in accent (off/on), articulation (staccato/legato), and L contour (as written/collapsed). One notable difference between blocks 2 and 4 was the consistent presentation of R with accents off; this was done to mimic more closely the source materials. In addition, the combination of layers allowed for the manipulation of their relative registral position (low/high). The articulation of each layer was also modified to facilitate focal attending. In particular, the sparser L-high was presented with legato articulation to make it more audible, and the denser R-low featured staccato articulation in an effort to alleviate its interference with L-high. Given the number of variables and the necessary limitations of one experimental session, within-layers and between-layers conditions were not balanced, resulting in a 2 × 4 factorial design with attended layer (L/R) and condition (each of the four stimuli) as within-subjects variables, but a number of confounds. This design allowed for an investigation of the relative salience of each attended layer as well as an exploration of the effect of different combinations of musical parameters on participants' tapping performance.
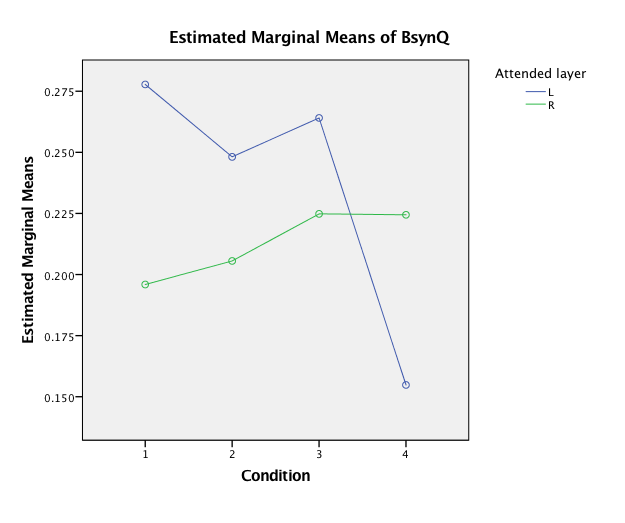
Fig. 3. Interaction of attended layer and condition for BsynQ in block 4 (estimated marginal means are expressed as fractions). The significantly lower percentage of quarter-note beats that were synchronized to in the L-attend condition for C4 is consistent with a detrimental effect of the register reversal on participants' tapping synchronization performance.
A univariate ANOVA was performed with attended layer (L-attend/R-attend) and condition (C1 through C4; refer back to Table 2 for details) as within-subjects variables. Attended layer had a significant main effect on CV and TsynQ, but not on BsynQ. Participants' tapping performance was more stable when attending L than R (.306 as compared to .462), F(1, 26) = 11.977, p = .002, and a larger proportion of participants' taps were synchronized with the quarter-note beat when attending L (30.0 as compared with 23.6% for R-attend), F(1, 26) = 8.980, p = .006. The specific combination of variables featured in each condition also had a significant main effect on TsynQ, F(3, 78) = 4.453, p = .012. Participants' tapping synchronization performance was significantly poorer for C4 (23.3 as compared with 29.1% for C3, p = .036); there was also a trend toward significance in the same direction for BsynQ, F(3, 78) = 2.843, p = 0.56. Finally, although condition did not have a main effect on CV, F(3, 78) = 1.943, p = .164, its effect was not negligible as participants' tapping was significantly less stable with C4 than C1 (M = 0.086, SE = 0.026, p = .017). This finding was also reflected in a significant interaction of attended layer and condition for both TsynQ and BsynQ, F(3, 78) = 3.602, p = .043, and F(3, 78) = 4.459, p = .013, respectively. Although participants synchronized with a generally higher number of quarter-note beats (BsynQ) in the L- than R-attend condition, the number of quarter-note beats synchronized to for C4 was significantly lower in the L-attend condition (15.5 as compared with 22.4% in the R-attend condition; see Figure 3). 16 These results suggest that register reversal had a detrimental effect on participants' synchronization with QL, which could be due to a greater interference of R when presented in the low register and/or a beat induction bias in favor of the low register.
Table 11 presents the results of the phase discrimination analysis (paired-samples t tests) for each condition within block 4. When comparing participants' downbeat synchronization within attended-layer conditions, it can be observed that the quarter-note beat was mensurally determinate only in four out of eight trials, all of which involved the L-attend condition. For three of the L-attend trials (C1, C2, and C3), participants synchronized significantly more with QL than QR, t(27) = 3.283, p =.003 (C1), t(27) = 3.467, p =.002 (C2), and t(28) = 2.881, p =.008 (C3). However, when attending to L in the high register, participants synchronized significantly more with the upbeats (QR), resulting in R-phase dominance, t(28) = 2.083, p =.047 (C4). In contrast, when participants tapped in the R-attend condition, their tapping consistently gave rise to phase ambiguity, t(26) = 1.286, p =.210 (C1), t(28) = .469, p =.643 (C2), t(29) = .553, p =.585 (C3), and t(29) = 1.083, p =.288 (C4). These results are consistent with the suggested bias in favor of the low register for beat induction.
| ATTENDED LAYER (L/R) | ACCENT (ON/OFF) | ARTICULATION (STA/LEG) | CONTOUR (ASW/COL) | REGISTER (LOW/HIG) | BsynQL vs. BsynQR (MEAN %) | Phase Profile | |
|---|---|---|---|---|---|---|---|
| C1 | L | on | staccato | as written | low | 27.0 > 10.8* | QL |
| R | off | legato | - | high | 22.9 > 19.6 | QA | |
| C2 | L | off | legato | collapsed | low | 24.4 > 15.0* | QL |
| R | off | legato | - | high | 21.0 > 20.1 | QA | |
| C3 | L | off | legato | as written | low | 25.6 > 13.9* | QL |
| R | off | staccato | - | high | 22.4 > 21.4 | QA | |
| C4 | L | on | legato | as written | high | 15.2 < 21.7* | QR |
| R | off | staccato | - | low | 19.2 < 21.3 | QA |
Note: * = p < .05
EFFECT OF TEXTURE (BLOCK 2 VS. BLOCK 4) AND PITCH (BLOCK 3 VS. BLOCK 4)
The experimental design allowed for an exploratory analysis of the effect of texture and pitch in a limited set of conditions. In block 4, C3 had been constructed by superposing two conditions from block 2, i.e., L-off.leg.asw.low and R-off.sta.hig. A paired-samples t test found no significant difference for any of the dependent variables between each segregated condition and their corresponding attended layer in the combined condition.
The four conditions in block 4 were built using two accentual templates from block 3: (1) L-on with R-off (C1 and C4), and L-off with R-off (C2 and C3). Each dependent measure from the two conditions in block 3 was used in four pairwise comparisons with the corresponding attended layers in block 4, including phase synchronization measures for the respective downbeat and upbeat phases. Because the task in block 3 involved global rather than focal attention, and thus encouraged integrated rather than streamed perception of the combined temporal sequences, these analyses allow for the exploration of the global effect of pitch structure, and the textural streaming it affords.
Table 12 presents the tapping variability results across blocks 3 and 4. When attending to L-off in the pitch-on condition, participants' tapping was significantly more stable for C2; there was also a trend in the same direction for tapping while attending L-off in C3. On the other hand, there was no significant difference in tapping variability for the pitch-on conditions involving L-on (C1 and C4). Participants' tapping variability was consistently higher when attending R-off, although this difference was only significant for C4. Thus, it would appear that textural streaming had a significant effect on participants' tapping behavior only for a limited set of conditions (C2 and C4), and that this effect was beneficial only when attending the condition that featured L-off with collapsed contour in the low register.
| BLOCK 3 (PITCH OFF) | BLOCK 4 (PITCH ON) | CV B3 vs. B4 (MEAN) | SIGNIFICANCE (2-TAILED) | |||||
|---|---|---|---|---|---|---|---|---|
| ACCENT (L/R, ON/OFF) | CONDITION | ATTENDED LAYER (L/R) | ARTICULATION (LEG/STA) | REGISTER (LOW/HIG) | CONTOUR (ASW/COL) | |||
| L-off | R-off | 2 | L | legato | low | collapsed | .388 > .287* | t(27) = 3.228, p = .003 |
| R | legato | high | - | .391 < .421 | t(28) = .483, p = .633 | |||
| 3 | L | legato | low | as written | .388 > .310 | t(28) = 1.950, p = .061 | ||
| R | staccato | high | - | .392 < .524 | t(29) = 1.345, p = .189 | |||
| L-on | R-off | 1 | L | staccato | low | as written | .346 > .259 | t(26) = 1.422, p = .167 |
| R | legato | high | - | .346 < .428 | t(26) = .988, p = .322 | |||
| 4 | L | legato | high | as written | .346 < .367 | t(27) = .258, p = .798 | ||
| R | staccato | low | - | .347 < .490* | t(28) = 2.251, p = .032 | |||
Note: * = p < .05
The results from the phase synchronization analysis, which compared each accent and attended-layer condition across blocks 3 and 4, are presented in Table 13. For each attended-layer condition, comparisons are shown for both downbeat and upbeat phases. Given the textural streaming afforded by the presence of pitch in block 4, it was expected that participants' synchronization performance would be higher with the quarter-note beat of the attended layer (downbeat phase) and lower with the quarter-note beat of the competing layer (upbeat phase).
Table 13a presents the results for L-phase synchronization. As can be observed, L-attend induced participants to synchronizing significantly more with QL (downbeat phase) in the combined layers with pitch on only for C3. Furthermore, when participants attended to L-on in C4, the condition that featured register reversal, they actually synchronized with a significantly lower number of QL. As the corresponding condition in block 3 only afforded accentual streaming in favor of QL, this finding suggests that participants might not have been able to perform the task, possibly due to the interference of R in the low register; it is also possible that the large leaps featured in L with the contour as written also contributed to the difficulty experienced by participants in attending that layer. On the other hand, R-attend did not induce participants to synchronize significantly less with QL (upbeat phase), although there was a trend toward significance in the expected direction for both L- and R-attend in C1 (the condition corresponding to the composer's notated version).
Table 13b presents the results for R-phase synchronization. When attending R, participants synchronized with a significantly higher number of QR (downbeat phase) for the combined layers with pitch on only when R was in the low register (C4), although there was trend toward significance in the same direction for C3 (which also features R with staccato articulation). As expected, when participants attended L, they synchronized with a significantly lower number of QR, except for C1 (the only condition that features L with staccato articulation). On the other hand, when attending L in C4, participants synchronized significantly more with QR, which is consistent with previous observations of a detrimental effect of the register reversal.
| BLOCK 3 (PITCH OFF) | BLOCK 4 (PITCH ON) | TsynQL B3 vs. B4 (MEAN %) | SIGNIFICANCE (2-TAILED) | BsynQL B3 vs. B4 (MEAN %) | SIGNIFICANCE (2-TAILED) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| ACCENT (L/R, ON/OFF) | CONDITION | ATTENDED LAYER (L/R) | ARTICULATION (LEG/STA) | CONTOUR (ASW/COL) | REGISTER (LOW/HIG) | |||||
| L-off | R-off | 2 | L | legato | collapsed | low | 25.0 < 28.9 | t(27) = 1.544, p = .134 | 23.4 < 24.4 | t(27) = .325, p = .748 |
| R | legato | - | high | 24.9 > 23.0 | t(28) = 1.368, p = .182 | 22.8 > 21.0 | t(28) = .743, p = .464 | |||
| 3 | L | legato | as written | low | 24.6 < 34.0* | t(28) = 2.951, p = .006 | 23.0 < 25.6 | t(28) = .671, p = .507 | ||
| R | staccato | - | high | 24.6 > 23.9 | t(29) = .401, p = .691 | 22.4 = 22.4 | t(29) = .015, p = .988 | |||
| L-on | R-off | 1 | L | staccato | as written | low | 28.6 < 35.0 | t(26) = 1.784, p = .086 | 23.4 < 27.8 | t(26) = 1.095, p = .284 |
| R | legato | - | high | 28.6 < 23.9 | t(26) = 1.738, p = .094 | 23.4 > 22.9 | t(26) = .192, p = .849 | |||
| 4 | L | legato | as written | high | 28.4 > 22.1 | t(27) = 1.530, p = .138 | 23.3 > 15.5* | t(27) = 2.378, p = .025 | ||
| R | staccato | - | low | 28.3 > 25.5 | t(28) = .846, p = .405 | 23.1 > 19.5 | t(28) = 1.218, p = .233 | |||
Note: * = p < .05
| BLOCK 3 (PITCH OFF) | BLOCK 4 (PITCH ON) | TsynQR B3 vs. B4 (MEAN %) | SIGNIFICANCE (2-TAILED) | BsynQR B3 vs. B4 (MEAN %) | SIGNIFICANCE (2-TAILED) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| ACCENT (L/R, ON/OFF) | CONDITION | ATTENDED LAYER (L/R) | ARTICULATION (LEG/STA) | CONTOUR (ASW/COL) | REGISTER (LOW/HIG) | |||||
| L-off | R-off | 2 | L | legato | collapsed | low | 22.3 > 18.4 | t(27) = 1.935, p = .064 | 21.6 > 15.0* | t(27) = 2.418, p = .023 |
| R | legato | - | high | 22.5 < 22.8 | t(28) = .179, p = .859 | 21.1 > 20.1 | t(28) = .447, p = .658 | |||
| 3 | L | legato | as written | low | 22.5 > 18.6 | t(28) = 1.574, p = .127 | 21.7 > 13.9* | t(28) = 2.769, p = .010 | ||
| R | staccato | - | high | 22.7 < 24.8 | t(29) = 1.186, p = .245 | 21.2 < 21.4 | t(29) = .061, p = .952 | |||
| L-on | R-off | 1 | L | staccato | as written | low | 18.4 > 15.5 | t(26) = 1.010, p = .322 | 15.1 > 11.1 | t(26) = 1.464, p = .155 |
| R | legato | - | high | 18.4 < 23.1 | t(26) = 1.657, p = .109 | 15.1 < 19.6 | t(26) = 1.847, p = .076 | |||
| 4 | L | legato | as written | high | 18.4 < 27.7* | t(27) = 2.475, p = .020 | 15.1 < 22.2* | t(27) = 2.139, p = .042 | ||
| R | staccato | - | low | 18.8 < 24.2 | t(28) = 1.717, p = .097 | 15.3 < 21.6* | t(28) = 2.530, p = .017 | |||
Note: * = p < .05
In sum, it would appear that the layer-specific attending afforded by the presence of pitch led to a statistically significant increase in downbeat (in-phase) synchronization only for a limited set of conditions (L-attend in C3 and R-attend in C4). A statistically significant decrease in upbeat (anti-phase) synchronization was also observed only in a limited set of conditions (C2 and C3), both of which involved attending L in the low register with accents off and legato articulation, with contour either collapsed or as written. Finally, statistically significant differences in the opposite direction were observed for L-attend when the registral position of the two layers was reversed (C4), i.e., a decrease in synchronization to QL and an increase in synchronization to QR. One possible explanation for these results is that when L was in the high register, participants were not able to perform the task properly, possibly due to a distractor effect of R in the low register, an interpretation that is consistent with the finding that participants' tapping was significantly less stable in this condition.
Exploratory Analysis of Between-Subjects Variables
A series of two-way univariate repeated measures ANOVAs was conducted to test the influence of a number of between-subjects variables on all performance measures as well as possible interactions with the previously tested within-subjects variables (excluding those testable only through paired-samples t tests). Given the irregular temporal structure of the two layers and the added difficulty associated with focal attending, it was hypothesized that participants with more formal musical training (as represented by degree, i.e., no degree/bachelor's vs. master's/PhD) would exhibit lower tapping variability and higher synchronization percentages. The general characteristics of the source materials, which presented superposed contrasting rhythmic strands in two different registers of the piano, also prompted the exploration of the influence of participants' main instrument (piano/percussion, low melodic, high melodic) and self-reported piano skill level (none/beginner, intermediate, advanced/expert). The effect of gender was investigated from a purely exploratory perspective. Results will be reported separately for each between-subjects variable across all experimental blocks. Because of the sampling method (convenient sample) and the increased probability of error associated with repeated analyses with the same variables, these results should not be taken as conclusive. However, they are suggestive of the many factors that need to be taken into consideration when studying listeners' rhythmic percepts with performance tasks (such as tapping studies) using musical stimuli.
EFFECT OF GENDER
In block 1 (segregated layers, pitch off), participants' gender did not have a significant main effect on any of the performance measures, but there was a surprising significant interaction with accent for BsynQ. The previously observed beneficial effect of accent on participants' beat synchronization was significant for men, but not for women (31.9 and 21.8% for accents on and off, respectively, as compared with 21.6 and 20.1%), F(1, 27) = 10.188, p = .004; there was also a trend in the same direction for TsynQ, F(1, 27) = 3.203, p = .085. There was no significant interaction of gender with layer.
In block 2 (segregated layers, pitch on), participants' gender had a significant main effect on tapping variability. Women's tapping was significantly more variable than men's (.470 as compared with .313), F(1, 26) = 4.429, p = .045. Furthermore, there was a trend toward a significant interaction with layer for BsynQ, with women's performance being more consistent across layers (16.2 and 16.4% for L and R respectively, as compared to 24.8 and 17.0% for men), F(1, 26) = 2.947, p = .098. There was no significant interaction of gender with articulation.
In block 3 (combined layers, pitch off), there was also a significant main effect of gender for TsynQ, with women synchronizing significantly less often with QR than men (28.1 as compared with 33.4%), F(1, 27) = 4.794, p = .037. Furthermore, although L-accent had previously been found to have no significant main effect on any of the performance measures, there was a significant interaction of gender with L-accent for BsynQ, F(1, 27) = 7.025, p = .013. While men's beat synchronization did not differ significantly based the presence of accents in L, women synchronized with a significantly lower percentage of QL with L-on than L-off (15.4 and 24.7% for accents on and off, respectively, as compared with 24.0 and 22.0% for men). This finding is consistent with the differential effect of accent on beat synchronization based on gender previously observed in block 1.
Finally, there was no main effect of gender and no significant interaction with either attended layer or condition in block 4 (combined layers, pitch on), although there was a trend toward a significant interaction with attended layer for BsynQ, F(1, 25) = 3.170, p = .087. Men showed a tendency to synchronize with a relatively higher percentage of quarter-note beats when attending L than R, but not women (25.5% and 20.1% for L- and R-attend, respectively, as compared with 20.9 and 22.9%).
Overall, these results suggest that the presence of accents had a differential effect on tapping performance based on gender in both segregated and combined layers conditions. In particular, when layers were segregated with pitch off, the beneficial effect of accents on beat synchronization to QL was limited to men's tapping. On the other hand, when layers were combined with pitch off, women's tapping exhibited lower beat synchronization to QL with L-on than L-off, and lower beat synchronization to QR across accent conditions. A possible explanation is that the presence of accents in L could have induced women to synchronize with a slower consonant beat period (e.g., half-note beat). Additionally, women also exhibited more tapping variability with the segregated R layer with pitch on.
EFFECT OF FORMAL MUSICAL TRAINING
In the two blocks featuring pitch off (blocks 1 and 3), there was no significant main effect or interaction of formal musical training, but several trends were observed. In block 1 (segregated layers), participants with a more advanced musical degree tended to synchronize with a higher percentage of quarter-note beats than those with less training (27.6 as compared with 18.5%), F(1, 27) = 2.948, p = .097, and while participants' beat synchronization performance was generally higher with L than R, this difference was more pronounced for those participants with more training (34.0 and to 21.3% for L and R, respectively, as compared to 20.1 and 16.9% for participants with less training), F(1, 27) = 3.774, p = .063. In block 3 (combined layers), participants with more training also tended to achieve higher synchronization performance with QL than those with less training (24.4 and 24.8% for TsynQL and BsynQL, respectively, as compared with 19.1 and 16.1%), F(1, 27) = 4.092, p = .053, and F(1, 27) = 3.557, p = .070. There was also a trend toward a significant interaction of training with layer-specific accentuation. Participants' tapping synchronization was similar across conditions featuring L-on, but in conditions featuring L-off, participants with a more advanced degree achieved higher TsynQL than those with less training (21.4 and 23.0% for no degree/bachelor's and master's/PhD, respectively, as compared with 16.7 and 25.8% for L-off), F(1, 27) = 3.200, p = .085. Finally, while participants with more training exhibited more tapping variability in the conditions featuring R-off than R-on, participants with less training showed the reverse tendency (.354 and .277 for R-off and R-on, respectively, as compared with .393 and .533), F(1, 27) = 4.155, p = .051.
In the two blocks featuring pitch on (block 2 and block 4), participants with more formal musical training achieved significantly better tapping performance than participants with less training. Participants with a masters' or PhD had a significantly lower CV than participants with no degree or a bachelor's (309 and .331 for blocks 2 and 4, respectively, as compared with .492 and .510), F(1, 26) = 6.094, p = .020, and F(1, 25) = 4.804, p = .038. In block 2 (segregated layers), participants with more training also achieved higher beat synchronization than those with less training (22.2 as compared to 13.5%), F(1, 26) = 4.354, p = .047.
Overall, these results are highly suggestive of a variegated effect of temporal structure and accent on participants' tapping behavior, with more formal musical training providing an advantage in the pitch-on conditions. These results also suggest that in the pitch-off conditions, accented beats had a different effect on participants' tapping based on their level of musical training, with the presence of accents having a detrimental rather than beneficial effect on the tapping consistency of participants with less musical training.
EFFECT OF MAIN INSTRUMENT
The effect of main instrument on participants' tapping performance was limited to the segregated layers conditions (blocks 1 and 2) and participants' tapping variability. In block 1 (pitch off), there was a significant interaction of instrument with accent. When accents were off, participants who played either piano/percussion or a low melodic instrument exhibited a more stable tapping period than those who played a high melodic instrument (.262 and .327 as compared to .543), F(2, 26) = 4.236, p = .026; when accents were on, these differences were significantly less pronounced (.384, .359, and .450, respectively). This interaction also resulted in a trend toward a significant main effect of instrument on tapping variability, with participants whose main instrument was a high melodic instrument exhibiting higher tapping variability (.497 as compared with .323 and .343 for piano/percussion and low melodic, respectively), F(2, 26) = 2.970, p = .069. There was no significant interaction of instrument with layer.
In block 2 (pitch on), there was a significant main effect of instrument, with observed tapping variability in order of most stable to least stable for participants whose main instrument was categorized as piano/percussion (.242), low melodic (.368), and high melodic (.469), respectively, F(2, 25) = 3.988, p = .031; post hoc analyses revealed that only the mean difference between piano/percussion and high melodic was significant (M = .227, SE = .080, p = .028). There was also a trend toward a significant interaction of instrument and layer, F(2, 25) = 3.396, p = .050. While participants' tapping was generally more stable with L than R, this difference was least pronounced for participants who played a low melodic instrument (.351 and .385) and most pronounced for participants who played a high melodic instrument (.332 as compared with .606), with participants who played piano or percussion somewhere in between (.182 as compared with .303).
These results suggest that the previously reported effect of layer on tapping variability was not independent of main instrument, and in particular, that participants who play a high melodic instrument might have been more sensitive to the surface tempo fluctuations exhibited by the higher-register layer (R), inducing them to adjust their tapping period and/or phase more often.
EFFECT OF PIANO SKILL LEVEL
Reported piano skill level had a more limited effect on participants' tapping performance. In block 1, there was a significant interaction of piano with accent for tapping variability. Participants with little or no piano experience exhibited more stable tapping behavior in the accents-on than the accents-off conditions (.378 as compared to .522), while participants with more experience exhibited more consistent tapping behavior across accent conditions (.478 and as compared with .453 for intermediate, and .358 as compared with .256 for advanced/expert), F(2, 26) = 5.150, p = .013. In block 2, there was also a trend toward a main effect of piano on tapping variability, F(2, 25) = 2.820, p = .079. Pairwise comparisons showed that this was due to a more stable tapping behavior for participants with advanced- or expert-level piano skills as compared to those with intermediate-level skills (.244, SE = .068 as compared with .453, SE = .058, p = .082).
Although these findings suggest that accents might stabilize the tapping period of participants with less piano experience, it is not clear what particular aspects of piano instruction or experience would be responsible for this effect.
GENERAL DISCUSSION
Two of the main goals of this study were to assess the influence of style-specific expertise on listeners' tapping performance and to measure the relative degree of mensural determinacy of the implied quarter-note beat in two contrasting rhythmic sequences. The two rhythmic sequences used in this experiment exhibited a high degree of syncopation (left-hand layer) and an irregular rhythmic surface characterized by tempo fluctuations (right-hand layer). Consistency in tapping period over the whole experiment varied widely across individual participants and was significantly correlated with participants' passive and active exposure to twentieth-century music, with more exposure (up to about 10 hours) resulting in a more stable tapping period. Mean synchronization percentages were relatively low, especially when compared to previous studies that used actual music as source materials, with the highest mean percentage across experimental blocks accounting for less than one-third (31.9%) of participants taps and a little more than one-fourth (25.5%) of the available quarter-note beats, which were observed in segregated and combined layers with pitch off, respectively. For example, Drake and colleagues (2000), who used the widest range of musical styles (from J. S. Bach to Bartók), found that overall synchronization was generally very good (93%), with musicians achieving a higher degree of synchronization (98%) than nonmusicians (88%). Similarly, Snyder and Krumhansl (2001) observed mean synchronization percentages of about 80% for monotonic and pitch varied versions of ragtime excerpts, with the lowest mean synchronization percentages resulting from right-hand only versions (about 70%). In the present study, individual participants achieved the highest tapping synchronization percentages when segregated layers were presented with indeterminate pitch, but these conditions also gave rise to the largest variance across participants. These findings are consistent with previous studies that found that degree of syncopation is a good predictor of synchronization performance (Fitch & Rosenfeld, 2007; Toiviainen & Snyder, 2003), and that musical training provides an advantage in hierarchical meter processing (Geiser et al., 2010; Palmer & Krumhansl, 1990).
The third experimental goal was to identify some of the musical parameters and participants' characteristics that could influence listeners' perception of an implied beat. Both tapping period and phase synchronization were found to be influenced by a number of factors, including order of presentation, global temporal structure (as represented by layer and texture, when textural streaming was not possible), and accentuation (intensity accents applied to whole-note or quarter-note beats). Exploratory analyses of a number of additional musical parameters (global pitch structure, articulation, contour, attended layer, and register) and participants' characteristics (gender, formal musical training, main instrument, and piano skill level) also suggest that other factors could have contributed to participants' tapping performance and would require further testing.
Mensural Determinacy and the Influence of Musical Parameters
Mensural determinacy was assessed by comparing participants' synchronization performance in each of the two phases of an interleaved quarter-note beat, as represented by each layer (L and R), across segregated and combined layers conditions. Table 14 presents a summary of the results of the phase discrimination analyses for each layer and condition in the four experimental blocks. Perceived mensural determinacy is understood as being represented by the phase profile associated with participants' spontaneous tapping, with significant differences in synchronization between the two phases of the quarter-note beat resulting in phase dominance (QL or QR = higher mensural determinacy), and lack of significant differences resulting in phase ambiguity (QA = lower mensural determinacy). The influence of some of the musical parameters on the mensural determinacy of each layer can be observed in the changes in phase profile from one set of conditions to another. Overall, the left-hand layer was generally perceived as being more mensurally determinate than the right-hand layer, with intensity accents and global pitch structure having a differential effect depending on layer and texture condition. As shown in Table 14a, when presented alone, the left-hand layer was perceived as being mensurally determinate regardless of pitch condition (off/on). In contrast, when presented alone, the right-hand layer was perceived as being mensurally determinate only when the quarter-note beats were accented and pitch was off (see Table 14b); when pitch was on, the right-hand layer was perceived as being mensurally ambiguous, pointing to an interaction of global temporal structure with global pitch structure that resulted in higher synchronization to the upbeat, an effect that remains to be systematically investigated. In the first experimental block with segregated layers and pitch off, higher degree of mensural determinacy for the left-hand layer also manifested in a presentation order effect, with participants who heard and tapped to the left-hand layer first achieving higher synchronization performance than participants who heard and tapped to the right-hand layer first. This finding suggests that memory could play a role in the interpretation of metric structure in complex rhythmic sequences.
The superposition of the two layers in two different pitch conditions provided further insight into the influence of global temporal structure and streaming (both mensural and textural) on beat percepts in stratified textures. When the two layers were combined in the pitch-off condition, the textural integration of the two segregated layers appeared to promote R-phase dominance, with the accented right-hand phase of the quarter-note beat being perceived as mensurally determinate regardless of L-accent condition (see Table 14b). This result is not entirely surprising given the generally faster pace of events in the right-hand layer; it also points to a regularizing effect of the more mensurally determinate left-hand layer on the fluctuating series of events presented by the right-hand layer, not unlike that of the left-hand part in the ragtime pieces used by Snyder and Krumhansl (2001). On the other hand, when layer-specific attending was made possible by global pitch structure, attending to the left-hand layer led participants to perceive that layer as mensurally determinate, except when the right-hand layer was presented in the low rather than high register. Surprisingly, when participants attended to the left-hand layer in the high register, their tapping resulted in R-phase dominance, providing further evidence of the role of the low register in beat induction (Hove et al., 2014).
| BLOCK 1 (PITCH OFF) | BLOCK 2 (PITCH ON) | BLOCK 3 (L+R, PITCH OFF) | BLOCK 4 (L+R, PITCH ON) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ACCENT (OFF/ON) | PHASE PROFILE | ARTICULATION (LEG/STA) | CONTOUR (ASW/COL) | PHASE PROFILE | R-ACCENT (OFF/ON) | PHASE PROFILE | CONDITION | ATTENDED LAYER (L/R) | ARTICULATION (LEG/STA) | REGISTER (LOW/HIG) | CONTOUR (ASW/COL) | PHASE PROFILE |
| off | QL | staccato | as written | QL | off | QA | 2 | L | legato | low | collapsed | QL |
| R | legato | high | - | QA | ||||||||
| 3 | L | legato | low | as written | QL | |||||||
| R | staccato | high | - | QA | ||||||||
| legato | as written | QL | on | QR | - | - | - | - | - | - | ||
| on | QL | staccato | collapsed | QL | off | (QL) | 1 | L | staccato | low | as written | QL |
| R | legato | high | - | QA | ||||||||
| 4 | L | legato | high | as written | QR | |||||||
| R | staccato | low | - | QA | ||||||||
| on | QR | - | - | - | - | - | - | |||||
| BLOCK 1 (PITCH OFF) | BLOCK 2 (PITCH ON) | BLOCK 3 (L+R, PITCH OFF) | BLOCK 4 (L+R, PITCH ON) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ACCENT (OFF/ON) | PHASE PROFILE | ARTICULATION (LEG/STA) | PHASE PROFILE | L-ACCENT (OFF/ON) | PHASE PROFILE | CONDITION | ATTENDED LAYER (L/R) | ARTICULATION (LEG/STA) | REGISTER (LOW/HIG) | CONTOUR (ASW/COL) | PHASE PROFILE |
| off | QA | staccato | QA | off | QA | 2 | L | legato | low | collapsed | QL |
| R | legato | high | - | QA | |||||||
| 3 | L | legato | low | as written | QL | ||||||
| R | staccato | high | - | QA | |||||||
| legato | QA | on | (QL) | 1 | L | staccato | low | as written | QL | ||
| R | legato | high | - | QA | |||||||
| 4 | L | legato | high | as written | QR | ||||||
| R | staccato | low | - | QA | |||||||
| on | QR | legato | QA | off | QR | - | - | - | - | - | - |
| on | QR | - | - | - | - | - | - | ||||
In this experiment, mensural determinacy and the effect of various musical parameters, including accent and pitch, were only assessed globally. A more specific interpretation of the different structural factors leading to mensural determinacy in these two rhythmic sequences would require a closer analysis of the source materials, taking into account participants' synchronization percentages in the different experimental conditions. Nonetheless, the contrasting structure of the two layers affords some preliminary observations, especially in terms of the influence of first- and second-order periodicity on beat induction. The lower degree of mensural determinacy suggested by the ambiguous phase profile of the right-hand layer, which is characterized by frequent changes in the rate of surface (first-order) events, is consistent with previous findings that pulse finding appears to depend mostly on first-order relationships (e.g., Demany & Semal, 2002). The higher level of mensural determinacy of the left-hand layer and the observed differential effect of accents also provides further evidence of the influence of accent on the perception of second-order periodicity (Jones & Pfordresher, 1997); this is consistent with the finding that an unmetered series of acoustic events can be perceived as more regular if streaming (via loudness or pitch distance) gives rise to second-order periodicity (Carson, 2007).
Tapping Profiles and the Role of Style-Specific Expertise
Figures 4 and 5 present two contrasting examples of participants' tapping profiles for the four trials featuring segregated layers with pitch off (block 1), which were found to give rise to the highest mean tapping synchronization percentage across participants. These tapping profiles provide useful illustrations of the influence of accent and streaming on tapping behavior as well as of the challenges associated with an investigation of spontaneous beat percepts in complex rhythmic sequences.
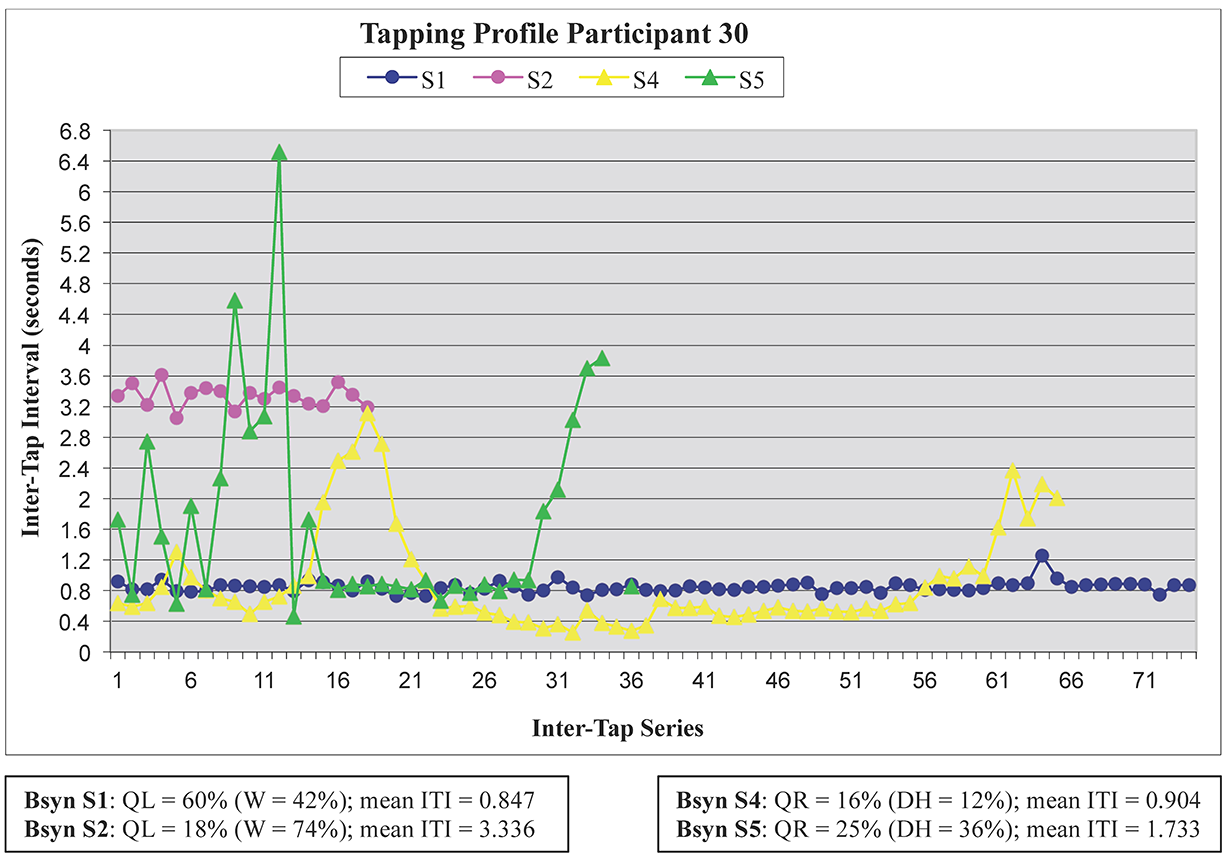
Fig. 4. Participant 30's tapping profile for the four trials in block 1 (S1 = L-off; S2 = L-on; S4 = R-off; S5 = R-on). Beat synchronization percentages (Bsyn) for the beat and measure pulse levels along with the mean inter-tap intervals (ITI) for each trial are given below the graph (QL/QR = quarter note; DH = dotted-half note; W = whole note). The left-hand tapping contours (S1 and S2) are representative of mensurally determinate tapping behavior, with a change of tapping period associated with the addition of accents at the whole-note pulse level (S2); the right-hand tapping contours (S4 and S5) are more variable, with temporary beat percepts that are only partially consonant with the implied beat structure.
The tapping profile of Participant 30 shows a clear contrast in tapping behavior depending on layer and accent condition. This participant's tapping to the more mensurally determinate left-hand layer resulted in relatively flat contours (S1 and S2), while the tapping to the unaccented right-hand layer (S4) was characterized by fluctuations in tapping period that closely match the written-out rubato, but still exhibited some mensural determinacy (e.g., inter-taps 42-55, M = 542 msec, SD = 52.36), with a tapping period that is partially consonant with the dotted-half note pulse (triplet quarter = 556 msec). The tapping contour of the accented right-hand layer (S5) also suggests some influence of the underlying short-long pattern created by the irregular subdivision of the durational pattern of a quarter note followed by a half note at the beginning of this excerpt (e.g., inter-taps 1-4, 5-8, and 13-15; see Appendix A, m. 68, beat 4, to m. 71). On the other hand, while the tapping period of the unaccented left-hand layer (M = 847 msec) is closely-related to the notated quarter-note beat (833 msec), that of the accented left-hand layer is more attuned to the whole-note "downbeat" (M = 3.336 as compared with 3.333 sec), resulting in a deceptively low beat synchronization percentage (18% of quarter-note beats synchronized to as compared to 74% for the whole-note pulse level).
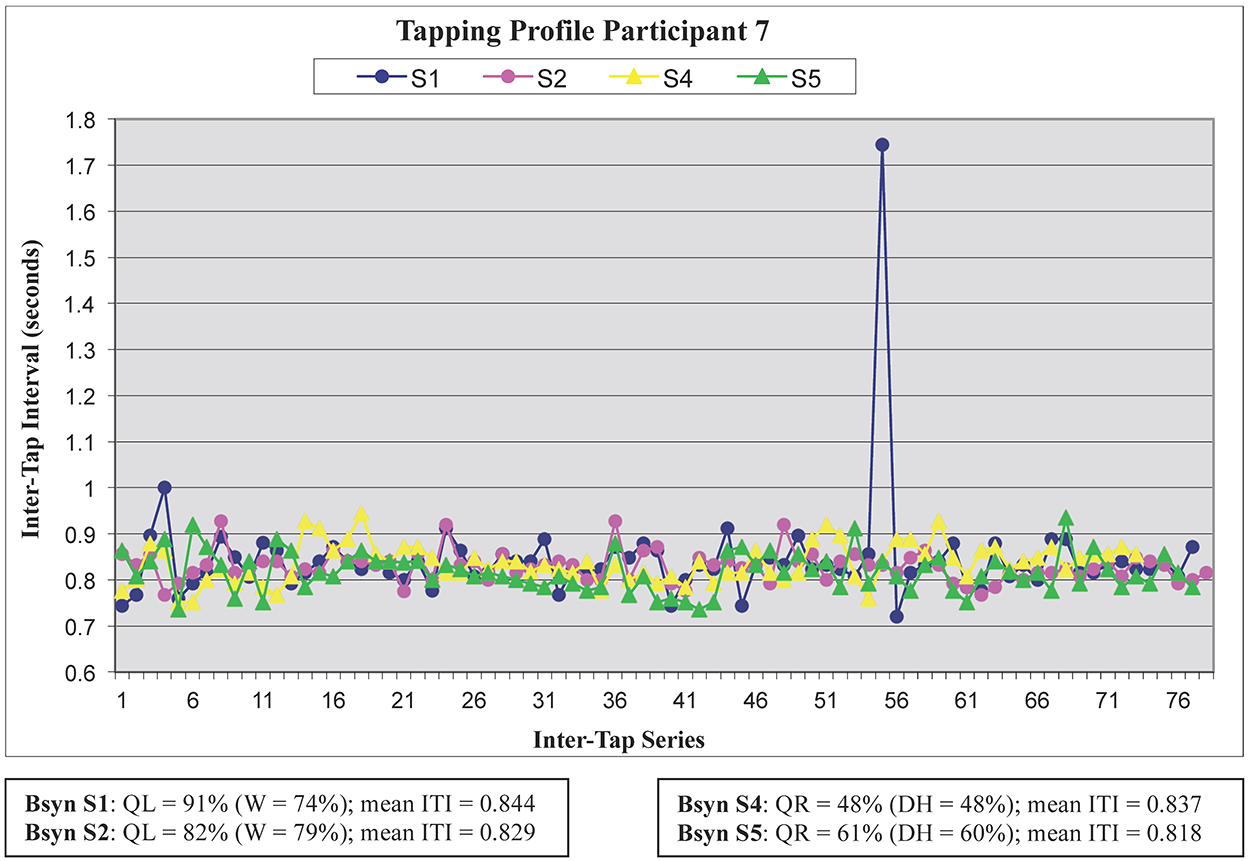
Fig. 5. Participant 7's tapping profile for the four trials in block 1 (S1 = L-off; S2 = L-on; S4 = R-off; S5 = R-on). Beat synchronization percentages (Bsyn) for the beat and measure pulse levels along with the mean inter-tap intervals (ITI) for each trial are given below the graph (QL/QR = quarter note; DH = dotted-half note; W = whole note). Although this participant's mean tapping period is fairly homogeneous across layer and accent conditions, the left-hand layer is perceived as more mensurally determinate than the right-hand layer, especially when the latter is unaccented.
In contrast, the tapping contours of Participant 7 (see Figure 5) are very similar across both layer and accent conditions, as attested to by the narrow range of their associated tapping periods (M = 818–844 msec). In fact, this participant's tapping behavior was remarkable both in its consistency and accuracy, with an overall coefficient of variability of merely 0.069 and beat synchronization percentages similar to those found in previous tapping studies using actual music as source materials (e.g., Snyder & Krumhansl, 2001). This tapping profile is also representative of the overall finding that the left-hand layer (S1 and S2) was perceived as more mensurally determinate than the right-hand layer, the latter exhibiting mensural determinacy only when it was accented (S5) or combined with the left-hand layer (not represented in this figure). The beat synchronization percentages displayed in Figure 5 also suggest that when tapping to the unaccented left-hand layer, this participant's beat percepts were more attuned to the quarter-note beat (BsynQL = 91%) than the whole-note pulse level (BsynW = 74%).
The exceptional tapping performance of Participant 7 provides an opportunity for a preliminary exploration of the communication process at play between a mechanical performance of the composer's score and a listener whose tapping behavior is representative of style-specific expertise.
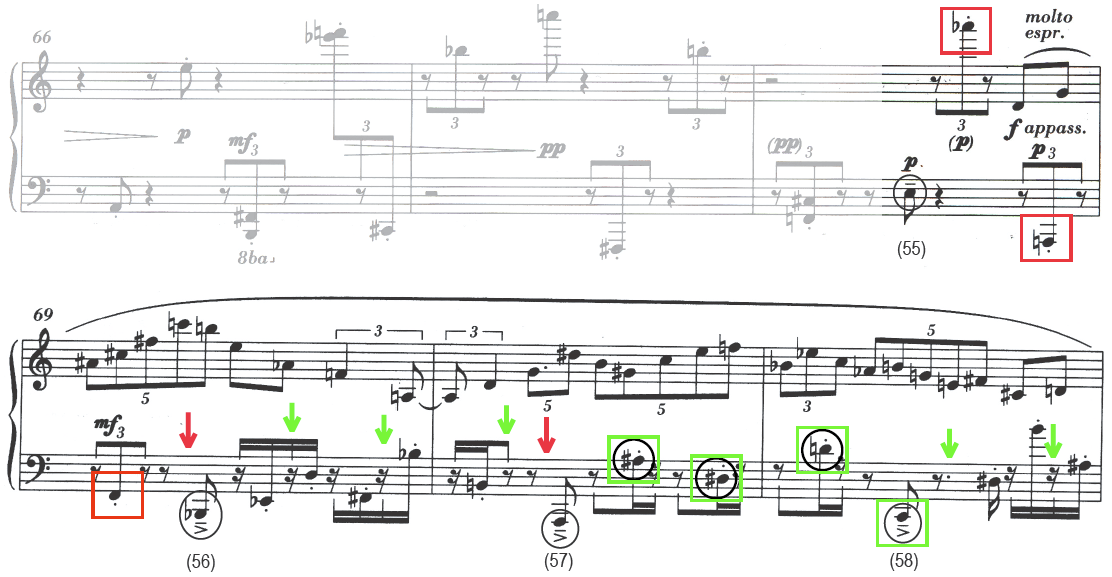
Fig. 6. Mapping of Participant 7's taps to L-off (pitch off), mm. 68–71 (red = false alarm; green = hit; square = surface event synchronized to; arrow = tap without surface event). The three false alarms at the beginning of the trial appear to be induced by displaced quarter-note beats.
Figures 6 and 7 offer a particularly effective representation of this communicative process and point to perceptual mechanisms that would require further investigation. In these figures, the first 14 taps of Participant 7 to each of two versions of the left-hand layer are matched to the notated score, allowing for closer observation of the interaction between tapping behavior and rhythmic structure. Taps synchronized with events are shown in boxes while taps that are not synchronized with a surface event are marked with arrows. In the first trial, which presented the unaccented left-hand layer with pitch off, the only "false alarms" (red boxes) were induced by a displaced periodicity equivalent to the quarter-note beat at the very beginning of the excerpt. Synchronization to these surface events led this participant to anticipate the whole-note pulse 56 (m. 69, red arrow), an error that was quickly corrected, as shown by successful synchronization to the following three implied quarter-note beats. Synchronization to the quarter-note beat is once more led astray, as shown by a second anticipated whole-note downbeat (pulse 57, m. 70, red arrow), possibly due to the influence of a series of offbeat events that exhibit a consonant but displaced period equivalent to the eighth-note pulse level, thus providing a suggestive example of the influence of first-order periodicity on beat tracking. Nevertheless, successful synchronization to sounded and implied quarter-note beats is once again quickly re-established and sustained for the remaining duration of this trial.
On the second trial with accented whole-note downbeats (see Figure 7), this participant was able to avoid synchronization with the displaced series of quarter-note beats, and synchronized with almost all of the quarter-note beats in this passage, even in the absence of corresponding sound events (the lower beat synchronization percentage for S2 shown in Figure 5 results from this participants' decision to stop tapping before the end of the trial, where the left-hand layer is particularly sparse; see Appendix B, mm. 85-88). This remarkable performance is suggestive of the role of tempo memory and intensity accents on beat tracking in irregular rhythmic sequences. Furthermore, within a conceptual framework that understands pulse finding and beat tracking as the product of a communication process between the composer and a listener, the displaced series of quarter-note beats in the very beginning (mm. 68-69), the presentation of a regular series of quarter-note beats a few measures later (mm. 70-71), and the presence of accented downbeats equivalent to a consonant whole-note pulse level suggest that in this passage, the composer may have been writing for listeners who have the necessary style-specific expertise to recognize beat clues, and would derive enjoyment from a playful manipulation of their temporal expectations.
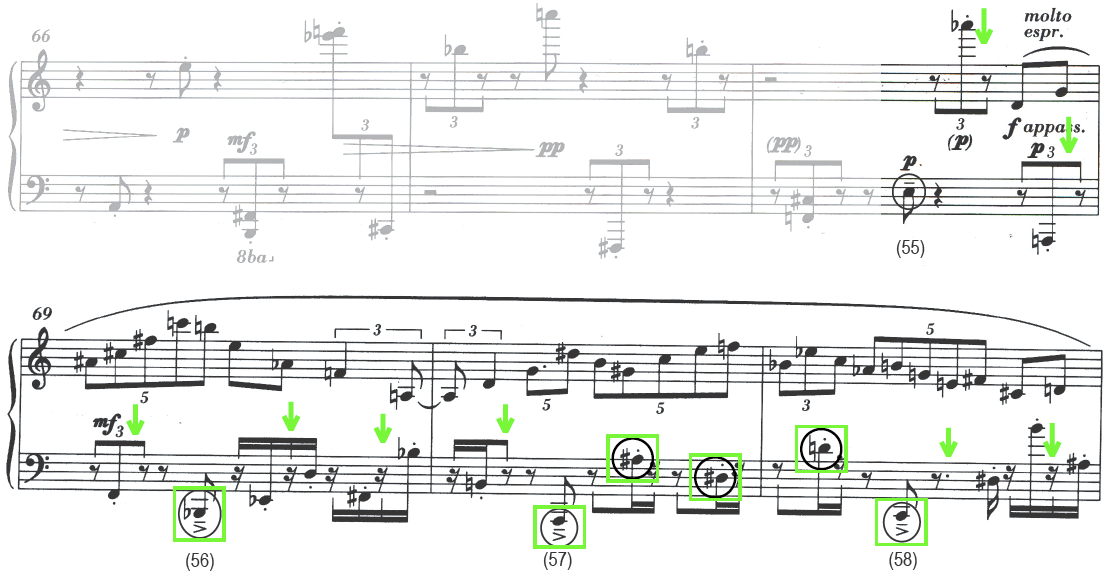
Fig. 7. Mapping of Participant 7's taps to L-on (pitch off), mm. 68–71 (red = false alarm; green = hit; square = surface event synchronized to; arrow = tap without surface event). In the second trial with accents on, this participant successfully avoided synchronizing with the initial series of displaced quarter-note beats.
CONCLUSION
Overall, the results of this experiment suggest that pulse finding in stratified textures representative of twentieth-century Western art music does require specialized skills, as demonstrated by the correlation of style-specific expertise with lower tapping variability as well as significant differences in tapping variability and synchronization based on formal musical training. It also appeared that while global temporal structure is the most consistent variable influencing participants' tapping performance, other musical parameters, in particular accent, texture, and register, may interact with each other and with between-subjects variables in various ways. In keeping with previous studies of polyrhythm, it would also appear that temporally stratified textures tend to produce downbeat ambivalence, and as shown by the observed shifts in phase profile from right- and left-hand phase dominance to phase ambiguity, when listeners are called to perform a pulse-finding task, the emergence of a mitigating pulse might be favored.
While style-specific expertise did correlate with a more stable beat period, the design of this experiment did not allow for the testing of the influence of style-specific expertise on the period and phase of the beat percepts. Musical training was observed to result in higher synchronization performance under certain accent and pitch conditions, but more analysis would be required to determine the degree of integration of the two streams under different pitch conditions, the exact nature of the alternative periodicities, and the specific relationship of taps and periodicities to the musical surface. Nonetheless, the findings and preliminary observations of individual tapping profiles point to an interaction between two different levels of attention in the auditory streaming of metrical structures: a low-level, tempo driven, perception of the beat (Scheirer, 1998), and a higher-level awareness of periodicity that calls on stream analysis and memory. At a minimum, these results call for a more systematic investigation of the effect of specific aspects of musical training on beat perception, especially in the context of complex rhythmic textures. Furthermore, questions of variability in tapping rate would also need to be considered more carefully, in particular with regard to the timing boundaries that can meaningfully be used in matching taps with sounded and implied beats, and identifying periodicities. Research on synchronization to expressive musical performances has shown that it is more difficult for participants to synchronize to performances that include the kind of timing variations applied by human performers (Drake, Penel, & Bigand, 2000). This is partly due to the fact that such timing variations often go beyond the usual window of tolerance used as reference for successful synchronization (here, 100 ms or 12% of the beat value). In many ways, Carter's notated score reproduces such timing variations, which also contributed to the difficulty of the task and may have played a part in the observed tapping variability and the resulting synchronization performance.
It is important to emphasize that the analytical interpretation used as a basis for the experimental design and statistical analysis of tapping performance in this study is not the only possible interpretation of the temporal structure exhibited by the source materials. In fact, participants' tapping responses represent a form of analysis, and the experimental task allowed participants to provide their own interpretation of the temporal structure. There was a significant degree of ambivalence in participants' tapping responses and a considerable number of taps either fell outside of the set limit of 100 msec or belonged to other pulse patterns. An in-depth analysis of the tapping patterns of a selected group of participants in tandem with the musical score could allow the analyst to identify specific structural elements at work, especially in terms of local temporal and pitch structures, which were not considered in this experiment other than in the most general manner (i.e., segregated versus combined layers and indeterminate versus determinate pitch). Beat synchronization percentages could also be used to identify passages that are perceived as being more or less mensurally determinate, and knowledge of Carter's compositional strategies could be used to generate hypotheses about the factors that contribute to the communication of pulse and meter in his music. The specific characteristics of the source materials could in turn inform the design of stimuli that would allow for a systematic investigation of the effect of a more limited number of factors on beat induction, without compromising ecological validity and within a conceptual framework that provides constructive differentiation in the realm of metric experience.
The exploratory analysis of between-subjects variables identified a number of effects and interactions, most of which have not been systematically explored in the literature on beat induction. In particular, some of the observed effects of gender are surprising and have no theoretical basis. Given the relatively small population sample size, the possibility of a sampling error due to the specific characteristics of the participants in this study cannot be discounted. However, because these effects could not be tested directly, future research should examine the influence of gender on beat percepts, particularly in the context of the effect of accent on beat induction and tapping variability.
Other types of collected data not reported here (i.e., observations of body movements and verbal comments) suggested various avenues of research for future studies. Since many of the participants spontaneously engaged in complex bodily patterns involving more than one motor system, future studies could include a more formal analysis of these patterns. This approach might prove particularly fruitful for the study of competing periodicities, especially given the fact that tapping superimposed beat structures seems to require integrative processing, and thus might not be fully representative of perceived temporal structures. Future research could also address the influence of counting and grouping strategies on tapping performance, especially in terms of beat synchronization. Another potentially rich field of investigation suggested by participants' verbal comments is spontaneous imagery as a product of meter perception.
Overall, it would seem that multi-modal approaches, and the complementary use of experimental methods and score analysis, might help us move closer to a richer understanding of the communication process at play in the temporal experience of complex rhythmic sequences. Given the wide variations in participants' musical training and the far-reaching implications of daily involvement with music, these studies should not limit their investigation to a statistical evaluation of tapping responses but also pay attention to the interaction of compositional strategies and listeners' style-specific expertise.
ACKNOWLEDGEMENTS
This article was copyedited by Tanushree Agrawal and layout edited by Kelly Jakubowski.
90+ by Elliott Carter
© Copyright 1994 by Hendon Music, Inc.
Reprinted by Permission, 2018.
NOTES
- Correspondence can be addressed to: Dr. Ève Poudrier, University of British Columbia, 6361 Memorial Road, Vancouver, BC V6T 1Z2, Canada, eve.poudrier@ubc.ca.
Return to Text - Focal attention, thus, can be understood as a particular type of selective attention (Jones et al., 1995) in which participants are prompted to attend to a specific pulse level rather than a specific strand in a given texture. Jones and colleagues (1995) contrast selective attention to integrative attention, which requires participants to listen to the stimulus as a whole.
Return to Text - In addition to pulse finding tasks, other common methods used in behavioral experiments on rhythm and meter perception include production and perceptual tasks (e.g., pattern reproduction and perturbation paradigms). In general, the findings from these studies are consistent with those that use a tapping paradigm.
Return to Text - In Hasty's (1997) words: "Mensural determinacy is the possibility for achieving a more or less definite, reproducible, duration or durational quantity—a potentiality that may be realized in an actual duration but never exhausted in a realization." (p. 220)
Return to Text - It is outside the scope of this article to consider the specific interaction of rhythm with pitch, which is nonetheless an important aspect of measuring complexity.
Return to Text - In an in-depth review of the different ways of measuring rhythmic complexity, Thul (2008) identifies six categories of complexity measures, i.e., rhythmic syncopation, pattern matching, distance, information entropy, interonset interval histograms, and mathematical irregularity, each of which rests on isochronicity (or "evenness") to a lesser or greater extent.
Return to Text - Paul Riker provided technical assistance for programming and sound engineering.
Return to Text - Since all participants were exposed to the same computer-generated stimuli, there is no way to test whether panning had an effect on participants' behavior. Future studies could compare participants' responses to computer-generated stimuli with those of live performances.
Return to Text - Participants were given the option to repeat the tapping task if they were not satisfied with their interpretation of the underlying pulse, but most of them did not elect to do so. A record of repeat performances was kept, but only the first tapping response was used for statistical analysis. There were also a small number of "false starts" due to technical issues; the computer saved these as empty files which were discarded.
Return to Text - Panayotis Mavromatis created the scripts used for processing the data.
Return to Text - It is also possible that some participants overestimated the number of hours, a problem that is inherent to all measures based on self-reported data.
Return to Text - There was, however, a trend toward a significant interaction of order and layer for BsynQ, F(1, 27) = 2.986, p = .095.
Return to Text - The experimental design did not allow for the testing of an independent effect of registral or accentual streaming.
Return to Text - Because articulation was found to have no significant main effect or interaction, the confound between pitch and articulation was deemed to be reasonable.
Return to Text - The confound between pitch and articulation involving L-on.sta.col.low and R-on.leg.hig is only apparent here because findings are interpreted within, rather than across, layer conditions. On the other hand, the confound between pitch and articulation within the R conditions was deemed reasonable because articulation was previously found to have no significant main effect or interaction with pitch. However, because those results were associated with the accents-off conditions, they do not rule out a potential interaction of articulation and accent.
Return to Text - Although there was a mean difference in the same direction between participants' tapping synchronization (TsynQ) in the L-attend and R-attend conditions for C4 (21.7 and 24.8%), it was not statistically significant.
Return to Text
REFERENCES
- Bregman, A. S. (1990). Auditory scene analysis: The perceptual organization of sound. Cambridge, Mass.: MIT Press.
- Carter, E. (1994). 90+ for piano. New York: Hendon Music, Boosey & Hawkes.
- Carson, B. (2007). Perceiving and distinguishing simple timespan ratios without metric reinforcement. Journal of New Music Research, 36(4), 313-336. https://doi.org/10.1080/09298210802015898
- Demany, L., & Semal, C. (2002). Limits of rhythm perception. Quarterly Journal of Experimental Psychology, 55A(2), 643-657. https://doi.org/10.1080/02724980143000406
- Drake, C., & Bertrand, D. (2003). The quest for universals in temporal processing in music. In I. Peretz & R. J. Zatorre (Eds.), The cognitive neuroscience of music (pp. 21-31). New York: Oxford University Press. https://doi.org/10.1093/acprof:oso/9780198525202.003.0002
- Drake, C., Jones, M. R., & Baruch, C. (2000). The development of rhythmic attending in auditory sequences: Attunement, referent period, focal attending. Cognition, 77(3), 251-288. https://doi.org/10.1016/S0010-0277(00)00106-2
- Drake, C., Penel, A., & Bigand, E. (2000). Tapping in time with mechanically and expressively performed music. Music Perception, 18(1), 1-23. https://doi.org/10.2307/40285899
- Fitch, W. T., & Rosenfeld, A. J. (2007). Perception and production of syncopated rhythms. Music Perception, 25(1), 43-58. https://doi.org/10.1525/mp.2007.25.1.43
- Franěk, M., Radil, T., & Indra, M. (1988). Tracking irregular acoustic patterns by finger tapping. International Journal of Psychophysiology, 6, 327-330. https://doi.org/10.1016/0167-8760(88)90020-7
- Geiser, E., Sandmann, P., Jäncke, L., & Meyer, M. (2010). Refinement of metre perception: Training increases hierarchical metre processing. European Journal of Neuroscience, 32(11), 1979-1985. https://doi.org/10.1111/j.1460-9568.2010.07462.x
- Grahn, J. A. (2009). Neuroscientific investigations of musical rhythm: Recent advances and future challenges. Contemporary Music Review, 28(3), 251-277. https://doi.org/10.1080/07494460903404360
- Handel, S. (1984). Using polyrhythms to study rhythm. Music Perception, 1(4), 465-484. https://doi.org/10.2307/40285273
- Handel, S., & Lawson, G. R. (1983). The contextual nature of rhythmic interpretation. Perception & Psychophysics, 34(2), 103-120. https://doi.org/10.3758/BF03211335
- Handel, S., & Oshinsky, J. S. (1981). The meter of syncopated auditory polyrhythms. Perception & Psychophysics, 30(1), 1-9. https://doi.org/10.3758/BF03206130
- Hannon, E. E., Soley, G., & Ullal, S. (2012). Familiarity overrides complexity in rhythm perception: A cross-cultural comparison of American and Turkish listeners. Journal of Experimental Psychology: Human Perception and Performance, 38(3), 543-548. https://doi.org/10.1037/a0027225
- Hannon, E. E., & Trehub, S. E. (2005a). Metrical categories in infancy and adulthood. Psychological Science, 16(1), 48-55. https://doi.org/10.1111/j.0956-7976.2005.00779.x
- Hannon, E. E., & Trehub, S. E. (2005b). Tuning in to musical rhythms: Infants learn more readily than adults. Proceedings of the National Academy of Sciences of the United States of America, 102(35), 12639-12643. https://doi.org/10.1073/pnas.0504254102
- Hannon, E. E., Vanden Bosch der Nederlanden, C. M., & Tichko, P. (2012). Effects of perceptual experience on children's and adults' perception of unfamiliar rhythms. Annals of the New York Academy of Sciences, 1252(1), 92-99. https://doi.org/10.1111/j.1749-6632.2012.06466.x
- Hasty, C. F. (1997). Meter as rhythm. New York: Oxford University Press.
- Hove, M. J., Marie, C., Bruce, I. C., & Trainor, L. J. (2014). Superior time perception for lower musical pitch explains why bass-ranged instruments lay down musical rhythms. Proceedings of the National Academy of Sciences of the United States of America, 111(28), 10383-10388. https://doi.org/10.1073/pnas.1402039111
- Iversen, J. R., Patel, A. D., & Ohgushi, K. (2008). Perception of rhythmic grouping depends on auditory experience. Journal of the Acoustical Society of America, 124(4), 2263-2271. https://doi.org/10.1121/1.2973189
- Jones, M. R., Jagacinski, R. J., Yee, W., Floyd, R. L., & Klapp, S. T. (1995). Tests of attentional flexibility in listening to polyrhythmic patterns. Journal of Experimental Psychology: Human Perception and Performance, 21(2), 293-307. https://doi.org/10.1037/0096-1523.21.2.293
- Jones, M. R., & Pfordresher, P. Q. (1997). Tracking musical patterns using joint accent structure. Canadian Journal of Experimental Psychology, 51(4), 271-290. https://doi.org/10.1037/1196-1961.51.4.271
- Jones, M. R., & Yee, W. (1997). Sensitivity to time change: The role of context and skill. Journal of Experimental Psychology: Human Perception and Performance, 23(3), 693-709. https://doi.org/10.1037/0096-1523.23.3.693
- Keller, P. E., & Burnham, D. K. (2005). Musical meter in attention to multipart rhythm. Music Perception, 22(4), 629-661. https://doi.org/10.1525/mp.2005.22.4.629
- Large, E. W., & Jones, M. R. (1999). The dynamics of attending: How people track time-varying events. Psychological Review, 106(1), 119-159. https://doi.org/10.1037/0033-295X.106.1.119
- Lempel, A., & Ziv, J. (1976). On the complexity of finite sequences. IEEE Transactions on Information Theory, 22(1), 75-81. https://doi.org/10.1109/TIT.1976.1055501
- Madison, G. S., & Merker, B. H. (2002). On the limits of anisochrony in pulse attribution. Psychological Research, 66(3), 201-207. https://doi.org/10.1007/s00426-001-0085-y
- Magill, J. M., & Pressing, J. (1997). Asymmetric cognitive clock structures in West African rhythms. Music Perception, 15(2), 189-222. https://doi.org/10.2307/40285749
- Martens, P. A. (2011). The ambiguous tactus: Tempo, subdivision benefit, and three listener strategies. Music Perception, 28(5), 433-448. https://doi.org/10.1525/mp.2011.28.5.433
- Palmer, C., & Krumhansl, C. L. (1990). Mental representations for musical meter. Journal of Experimental Psychology: Human Perception and Performance, 16(4), 728-741. https://doi.org/10.1037/0096-1523.16.4.728
- Parncutt, R. (1994). A perceptual model of pulse salience and metrical accent in musical rhythms. Music Perception, 11(4), 409-464. https://doi.org/10.2307/40285633
- Poudrier, È., & Repp, B. H. (2013). Can musicians track two different beats simultaneously? Music Perception, 30(4), 369-390. https://doi.org/10.1525/mp.2013.30.4.369
- Povel, D. (1984). A theoretical framework for rhythm perception. Psychological Research, 45(4), 315-337. https://doi.org/10.1007/BF00309709
- Povel, D., & Essens, P. (1985). Perception of temporal patterns. Music Perception, 2(4), 411-440. https://doi.org/10.2307/40285311
- Rammsayer, T., & Altenmüller, E. (2006). Temporal information processing in musicians and nonmusicians. Music Perception, 24(1), 37-48. https://doi.org/10.1525/mp.2006.24.1.37
- Repp, B. H. (2005). Sensorimotor synchronization: A review of the tapping literature. Psychonomic Bulletin Review, 12(6), 969-992. https://doi.org/10.3758/BF03206433
- Repp, B. H. (2007). Perceiving the numerosity of rapidly occurring auditory events in metrical and nonmetrical contexts. Perception & Psychophysics, 69(4), 529-543. https://doi.org/10.3758/BF03193910
- Repp, B. H., London, J. M., & Keller, P. E. (2005). Production and synchronization of uneven rhythms at fast tempi. Music Perception, 23(1), 61-78. https://doi.org/10.1525/mp.2005.23.1.61
- Repp, B. H., & Su, Y. (2013). Sensorimotor synchronization: A review of recent research (2006–2012). Psychonomic Bulletin Review, 20, 403-452. https://doi.org/10.3758/s13423-012-0371-2
- Scheirer, E. D. (1998). Tempo and beat analysis of acoustic musical signals. Journal of the Acoustical Society of America, 103(1), 588-601. https://doi.org/10.1121/1.421129
- Shmulevich, I., & Povel, D. (2000). Measures of temporal pattern complexity. Journal of New Music Research, 29(1), 61-69. https://doi.org/10.1076/0929-8215(200003)29:01;1-P;FT061
- Snyder, J. S., Hannon, E. E., Large, E. W., & Christiansen, M. H. (2006). Synchronization and continuation tapping to complex meters. Music Perception, 24(2), 135-145. https://doi.org/10.1525/mp.2006.24.2.135
- Snyder, J. S., & Krumhansl, C. L. (2001). Tapping to ragtime: Cues to pulse finding. Music Perception, 18(4), 455-489. https://doi.org/10.1525/mp.2001.18.4.455
- Tanguiane, A. S. (1993). Artificial perception and music recognition. Berlin: Springer-Verlag. https://doi.org/10.1007/BFb0019384
- Thul, E. (2008). Measuring the complexity of musical rhythm (Order No. MR67022). Available from ProQuest Dissertations & Theses Global. (787901819). Retrieved from https://search.proquest.com/docview/787901819
- Todd, N. P. M., Cousins, R., & Lee, C. S. (2007). The contribution of anthropometric factors to individual differences in the perception of rhythm. Empirical Musicology Review, 2(1), 1-13. https://doi.org/10.18061/1811/24478
- Toiviainen, P., & Snyder, J. S. (2003). Tapping to Bach: Resonance-based modeling of pulse. Music Perception, 21(1), 43. https://doi.org/10.1525/mp.2003.21.1.43
- Toussaint, G. T. (2013). The geometry of musical rhythm: What makes a "good" rhythm good? CRC Press, Taylor & Francis Group.
- Vinke, L. N. (2010). Factors affecting the perceived rhythmic complexity of auditory rhythms. Unpublished masters of arts thesis, Graduate College of Bowling Green State University, United States.
- Vuust, P., Wallentin, M., Mouridsen, K., Østergaard, L., & Roepstorff, A. (2011). Tapping polyrhythms in music activates language areas. Neuroscience Letters, 494(3), 211-216. https://doi.org/10.1016/j.neulet.2011.03.015
- Yeston, M. (1976). The stratification of musical rhythm. New Haven, CT: Yale University Press.
APPENDIX
A. Source materials extracted from Elliott Carter's 90+ for piano (1994), mm. 68, fourth eighth note, to 79.
B. Source materials extracted from Elliott Carter's 90+ for piano (1994), mm. 80 to 88, fifth sixteenth note.
C. Sound files referenced in this paper are available at: http://hdl.handle.net/1811/85871