BACKGROUND
THE structures of rhythm and meter in music consist of patterns of durational relations. However, the perception of rhythmic figures and metric periodicities depends on the tempo at which they are performed; the relational aspect of rhythmic and metric structure interacts with the absolute durations of its elements (Fraisse, 1982; Handel, 1991; Parncutt, 1994; Clayton, 1997; London, 2002; 2012; Repp, 2006). This paper concerns the perceptual constraint on the lower limit for meter (LLM), i.e., the threshold for the shortest inter-onset-intervals (IOIs) that we can integrate at the level of beat subdivision into a hierarchy of entrainable metric pulse-streams. The study of the LLM-threshold is relevant as an instance of the limits of human temporal perception in general and as a perceptual constraint framing style-specific conventions of music production, cognition, and aesthetic experience in particular. Event rates exceeding the LLM-threshold occur in many types of musical performance, yet they often appear only locally and tend to suggest a perception as an ornamental embellishment, rather than a rhythmic figure supported by a metric density referent. If a roll or trill is slowed down so that the IOIs between its elements exceed the LLM, it will lose its roll or trill quality. Conversely, if a rhythmic figure is sped up until the IOI of its density referent drops below the LLM, it will become difficult to cognize its structure and entrain to a potentially underlying beat periodicity. The concept of a LLM-threshold suggests that most music features rhythmic structures at tempos that permit metric density referent IOIs above that threshold. This does not however exclude the possibility that some styles or performers (and their audiences) use shorter durations and tolerate or even appreciate a blurring of metric perception whenever they approach or cross the threshold range.
Justin London (2002) proposes an LLM-threshold at around 100 ms, based on a survey of studies in subjective rhythmization, interval discrimination, cortical processing of musical elements, vocal articulation, and the timing of swing eighth notes in jazz music performance. Entrainable metric beats tend to display IOIs larger than 200–250 ms (Fraisse, 1982; Parncutt, 1994; Van Noorden & Moelants, 1999; Drake, Panel, & Bigand, 2000; Moelants, 2002). London argues that this fits in well with the hypothesis of an LLM-threshold at around 100 ms, since the pulse at the beat level in a metric hierarchy is characterized by lending itself to metric subdivision. A minimum duration of 100 ms for the subdivision would thus require a minimum duration of 200 ms for the beat in the case of a binary subdivision.
Bruno Repp (2003) tested the lower boundary of the smallest metrical subdivision to allow sensorimotor synchronization using a tapping task, and found an LLM-threshold at around 120 ms. Repp hypothesized a perceptual constraint and tried to avoid the effects of motor constraints. He therefore had participants synchronize (tap) with only every fourth onset in the series of rapid isochronous equitones used as a stimulus (1:4 tapping task). Synchronizing with each of the tones in the auditory stimulus (1:1 tapping), by contrast, is hard to perform with durations shorter than 200 ms (Fraisse, 1982; McAuley et al., 2006). This indicates that a bio-mechanic motor constraint on tapping at this range differs from the perceptual constraint at around 120 ms. Synchronization to a higher-level periodicity in a 1:4 tapping task is comparable with entrainment to a musical beat extracted from a rhythmic surface based on a quaternary beat subdivision. Repp's study of sensorimotor synchronization is thus directly pertinent to the question of metric subdivision in music perception, and a closer look into his findings called for. Repp estimated the LLM-threshold as the IOI that allows the average participant to successfully synchronize in more than half of the trials. However, the effect of the threshold—decrease in successful trials—occurs already at 170–160 ms and continues to strongly influence the tested behavior at durations shorter than 100 ms (see Figure 1). Evidently, the effect of the perceptual LLM-constraint occurs gradually around a very soft limit.
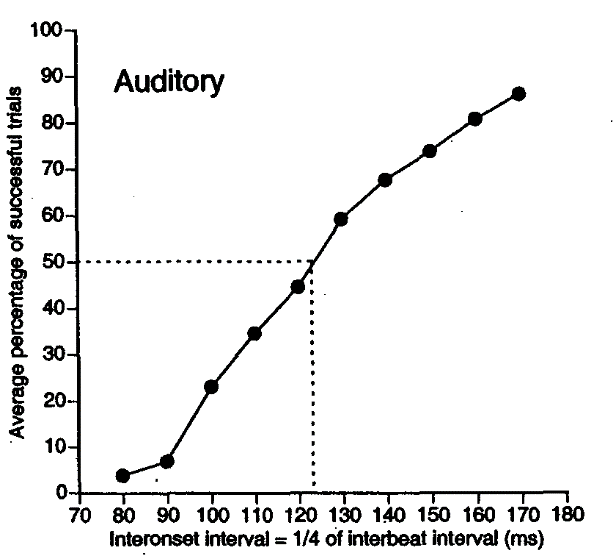
Fig. 1. Average percentage of successful synchronization trials as a function of IOI duration. The dotted line shows the estimation of the synchronization threshold (50% of successful trials) at 123 ms. Taken from Repp (2003, Figure 1-A).
Just as importantly, Repp (2003) found lower thresholds for trained musicians than for non-trained individuals and suggested that the more complex and interesting rhythms typically found in performed music might allow for metric subdivisions faster than the relatively dull isochronous equitones used in his laboratory experiments. On the other hand, rhythmic complexities such as anti-phase (off-beat) or non-isochronous (e.g., 2+3 or 2+2+3) tapping can again increase the minimum durations for successful synchronization (Repp, 2005a; 2005b; Repp, London, & Keller, 2005). As various survey articles emphasize (cf. London, 2002; Repp, 2006; McAuley, 2010), the LLM-threshold evidently varies according to context, task, and individual differences. Both this contingent variability and the gradual occurrence discussed above suggest a conception of the LLM as a soft threshold range of durations rather than as a single hard threshold value.
Friberg & Sundström (2002) studied the so-called swing ratio in jazz performance by measuring the ratio of the two different eighth notes' durations per quarter note beat (long–short). Measuring the ride cymbal onsets of four different drummers in excerpts of commercial recordings, they found that, generally speaking, the ratio tends to decrease from over 3:1 to 2:1 to close to 1:1, with increasing tempos ranging from 110 to 320 bpm. However, for medium to fast tempos (about 150–320 bpm), the duration of the short element in the long–short subdivision pattern was reported to be "approximately constant at about 100 ms" (337) independent of the ratio, suggesting a perceptual limit of metric subdivision. The data shows that the durations of the short notes actually fall to about 90 ms, however, with one player at about 84 ms (see Figure 2-A). The value of 100 ms was mentioned by the authors with the intention of providing only a rough estimate (Friberg, personal communication, 4/10/2016), yet was read more explicitly and contributed to specifying a 100 ms threshold in London 2002. Dittmar, Pfleiderer, & Müller (2015) analogously analyzed the swing ratio and durations in the ride cymbal performance in a corpus of 921 excerpts performed by ten different drummers. The range of performed tempos appeared to be similar (about 120–320 bpm) and the general trend of smaller ratios at higher tempos was replicated (Dittmar, Pfleiderer, & Müller, 2015, Figure 5-A). However, this study found that the short elements in the medium to high tempos (about 150–320 bpm) were not constant at a certain relatively narrow range of tempos, but continued to decrease. Moreover, the range of durations in the medium to fast tempos varied more widely, from about 120 ms down to about 80 ms, with two individuals and one outlier performance approximating 70 ms (see Figure 2-B).
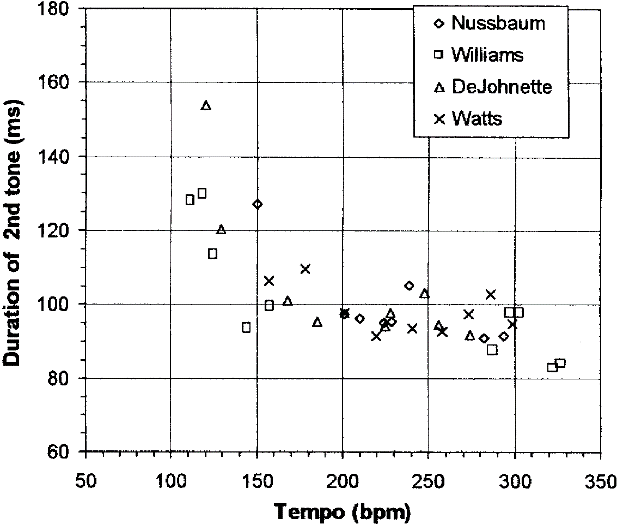
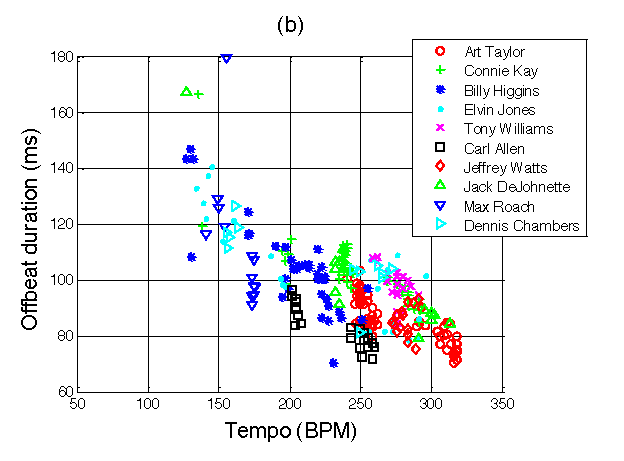
Fig. 2A (left) Durations of the short (off-beat) element in the ride cymbal performance of four jazz drummers at different tempos. Taken from Friberg & Sundström (2002, Figure 2).
Fig. 2B (right) Durations of the short (off-beat) element in the ride cymbal performance of ten jazz drummers at different tempos. Taken from Dittmar, Pfleiderer, & Müller (2015, Figure 5-B).
Collier & Collier (1994) analyzed the tempos within a large set of jazz recordings and found beat rates to be normally distributed between 50 bpm and 330 bpm. At 330 bpm, the binary subdivision has a mean duration of 91 ms. Assuming that a slight unevenness of the two subdivisions is still present due to swing timing, the short element's duration would be below 90 ms.
Ethnomusicological studies of xylophone music from Uganda reported subdivision IOIs of 100 ms as representing a standard performance tempo (Kubik, 1969; 1994; Cooke, 1970; Micklem, Cooke, & Stone, 1999). Given that it is unlikely for a performance practice to have identical standard and marginally rapid tempos, this would suggest that faster subdivisions are possible. I carried out spot measurements of some of the referenced field-recordings and found subdivision IOIs within a range of 85 ms characterizing entire pieces. 2 This closely corresponds to the possible 80–100 ms threshold hypothesized for jazz music above.
In summary, several papers suggested that the LLM-threshold is about 100–120 ms, yet tempos and subdivision durations reported for some styles of performed music suggest the alternative assumption that shorter subdivisions within a range of 80–100 ms may well be possible. The present paper aims to examine the latter assumption by the study of performance timings in West African percussion ensemble music.
APPROACH AND METHOD
I propose three conditions that must be met in order for a simple measurement of the most rapid beat rates of recorded live music performances to allow us to estimate the lower limit for metric subdivision durations in specific musical genres. First of all, a survey must define the fastest performances of a given repertoire. Second, music analysis must define the subdivision cardinality (e.g., binary, ternary, or quaternary); measured beat rates do not permit an inference of mean subdivision intervals until the cardinality of the subdivision has been reliably established. Third, the metrical status and function of the beat subdivision must be convincingly argued within the respective stylistic context. Given that these conditions are met, this type of comparative musicological approach to the LLM issue can draw on an abundance of carefully contextualized recordings created by ethnomusicologists all over the world.
The process of selecting recorded repertoires for this study began with a survey and spot measurements of ethnographic audio and video recordings of six well-researched traditions of West African dance drumming. Ewe drumming from southeastern Ghana and jembe drumming from southern Mali suggested themselves for closer inspection, as they displayed the fastest subdivision rates. 3 About 50 recordings of ten different pieces were then explored through tempo measurements of beginning, middle, and end section excerpts. Detailed measurements of full performances finally focused on twenty recordings with a total running time of about 90 minutes, ten of which make up the case studies presented below.
All of the studied pieces consist of composite ensemble rhythms that can be mapped onto a metric cycle of four beats with either a ternary or a quaternary beat subdivision. The first beat of each 4-beat cycle in the selected recordings was marked manually in the audio editing timeline of a video editor (Sony Vegas Professional). I performed the marking as a live tapping exercise, that is, by striking a key on the computer keyboard while listening to the recording, and later controlled each time-point by sight and adjusted the markers where necessary. I am experienced in this task, since marking metric cycles was my first approach to annotating hundreds of recordings over the course of two research projects dedicated to timing measurements in various traditions of West African drum ensemble music (2006–07 and 2011–2015). The primary marking was unproblematic and turned out to be relatively precise; errors rarely exceeded +/- 25 ms. I did not correct any errors smaller than that for two reasons. First, a potential error of 25 ms within the cycle IOI would amount to an error of only 1.6 or 2.1 ms, respectively, for the quaternary and ternary subdivisions to be studied, which is tolerable for the present research issue. Second, I will provide my findings primarily as moving averages. Thus, any measurement error for a certain 4-beat cycle will be leveled out by the negatively proportional error that results automatically in the adjacent metric cycle. The next step was to export the time-series of markers as text-files and import them to Microsoft Excel. Finally, dividing the measured cycle IOIs by the number of metric subdivisions present in the cycle resulted in the IOIs of the fastest pulse. I will argue the definition of subdivision cardinalities and their metric function in the following section on a general theoretical level and then rehearse it analytically in each of the case studies below.
Note that the procedure described above deliberately does not account for the different durations of distinct pulse classes in non-isochronous ("swung") subdivisions. 4 Rather than focusing on the duration of the shortest element in a swung subdivision timing pattern, it averages subdivision durations across metric cycles. In the same vein, I do not consider the most extremely short subdivision durations, which may occur during only a few subsequent cycles, but will rely exclusively on moving averages with mean values that are more or less stable in samples of at least 30 seconds running time. My intention is to argue for relatively conservative estimates of the shortest stable metric subdivisions.
DEFINING THE SMALLEST METRIC SUBDIVISION
As a first approach to determining the fastest metrically relevant subdivision in a piece, the fastest continuous stream of note onsets was counted; isolated rhythmic figures were not considered, nor were percussive embellishments such as flams or rolls.
In both Ewe drumming and Malian jembe drumming, there are pieces which do not display a density referent shared across all of the ensemble parts. In these pieces, a lead drummer, for instance, may frequently play quaternary subdivisions in an ensemble context characterized by ternary subdivisions. Such pieces are relatively difficult to analyze and do not lend themselves easily to discussions of the limits of metric perception. The pieces to be analyzed below were selected because they are less problematic in this respect; they all show a density referent that is shared quite consistently across ensemble parts. Their rhythmic textures are saturated to near-maximum, i.e., almost every time-point at the level of the fastest pulse receives a note onset. Typically, this onset stream is not performed by one single player, at least not for more than a few metric cycles. Instead, the fastest pulse generally consists of a composite polyrhythm resulting from the interweaving phrases of various ensemble members playing together. These near-continuous onset streams suggest a correspondence to metrically relevant beat subdivisions. Their periodicities mathematically represent the greatest common divisor underlying all durational proportions present in the rhythmic figures of each of the individual ensemble parts. We can thus assume two metric types in the repertoires under consideration: a 4-beat/16-subdivision cycle with quaternary beat subdivisions and a 4-beat/12-subdivision cycle featuring ternary subdivisions (see Tables 1 and 2).
| x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | continuous onset stream |
| ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | 16-subdivision sub-cycle |
| ⋅ | ⋅ | ⋅ | ⋅ | metric beat | ||||||||||||
| ⋅ | metric cycle | |||||||||||||||
| x | x | x | x | x | x | x | x | x | x | x | x | continuous onset stream |
| ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | 12-subdivision sub-cycle |
| ⋅ | ⋅ | ⋅ | ⋅ | metric beat | ||||||||
| ⋅ | metric cycle | |||||||||||
In the following, I present four partly interrelated arguments that converge towards the conclusion that the continuous onset stream as defined above does indeed constitute the fastest metrically relevant pulse.
A first step is to acknowledge the state of relevant research in ethnomusicology. The fastest consistent periodicity in African rhythms is generally conceived of as corresponding to the fastest layer of metric pulse (see Nketia, 1963; Dauer, 1966; Blacking, 1967; Koetting, 1970; Pantaleoni, 1972a; 1972b; 1972c; Kolinski, 1973; Kubik, 1988; 1994; Locke, 1979; 1982; 2009; Kauffman, 1980; Arom, 1984; Stone, 1985; Anku, 1988; 2000). A certain fetishizing of the metric relevance of the fastest pulse has also come under criticism (see Agawu 2003, 48–53, 64–68; 2006, 21). However, acknowledging that the beat (tactus) layer represents the main level of metric reference does not call into question that the fastest pulse also constitutes one of several layers in the metric hierarchy (see Locke, 1979, chapter 5; 1982; Agawu 2003, chapter 4; 2006). In summary, a common-sense assumption among ethnomusicologists is that the hierarchical reach of metric structure in African rhythm does not stop at the beat level—as is claimed, for instance, by some theories of meter for Western art music (Lerdahl & Jackendoff, 1983; Krebs, 1999; Mirka 2009)—but extends to the rhythmic surface/beat subdivision level.
A second argument in support of the metricality of the fastest pulse in West African drumming resides in the lack of plausible alternative hypotheses. Let me briefly consider the slower periodicities that come into question as candidates for the lowest level in the metric hierarchy. For pieces that feature sixteen fast onsets per cycle, one might hypothesize an 8-subdivision sub-cycle (see Table 3). In the case of a ternary subdivision, there is no such intermediate layer between the beat and rhythmic surface level. To discount the metrical salience of the 12-subdivision here amounts to assuming that the beat itself is the fastest metric layer, without any metrically relevant subdivision being present (see Table 4).
| x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | continuous onset stream |
| ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | 8-subdivision sub-cycle | ||||||||
| ⋅ | ⋅ | ⋅ | ⋅ | metric beat | ||||||||||||
| ⋅ | metric cycle | |||||||||||||||
| x | x | x | x | x | x | x | x | x | x | x | x | continuous onset stream |
| ⋅ | ⋅ | ⋅ | ⋅ | metric beat | ||||||||
| ⋅ | metric cycle | |||||||||||
The alternative hypotheses presented above are implausible. If they were true, half or two-thirds, respectively, of all consistently accented time-points in the metric cycle would not be anchored to the metric grid. This is all the more relevant as a study of statistical onset frequency distribution in jembe music from Mali demonstrates that these "off-beat" time-points tend to receive much rhythmic accentuation (London, Polak, & Jacoby, 2017). If it were true that the off-beat positions are not metrically integrated, then non-metrical rhythmic accents would precede and succeed every single metrically relevant rhythmic accent to occur in a piece. Such an infinite sweep of adjacent non-metric and metric accents would tend to mask the metric structure. One possible method of dealing with this would be to dedicate some specific instrument to accent only the metric periodicity with a sound distinct enough from the rest of the ensemble to allow for stream segregation (e.g., in terms of timbre, pitch, or loudness). These distinctly sounding temporal "landmarks" may afford entrainment to a metric beat while ignoring the turbulent surface rhythms. Such overt beat-marking is however not at all common in the repertoires under scrutiny. In summary, a continuous stream of onsets that is too fast to trigger a sense of a congruent (1:1) metric pulse-stream is equally unlikely to trigger stable metric entrainment to a higher-level metric pulse-stream (e.g., 2:1 or 3:1). The alternative hypotheses therefore do not make sense.
A third, more specific argument is that without the fast metric subdivisions, some prominent types of rhythmic figuration characteristic of the musical genres under scrutiny appear inconceivable. One such type is the so-called cross-rhythm, a rhythmic figure consisting of a sequence of events that systematically "crosses" the metric beat (see Table 5). Studies of African rhythm have offered diverging interpretations of cross-rhythm. Some claim that the tension between beat and cross-rhythm alludes to an alternative beat and that the perceptual rivalry of alternative beat options—a state of metric ambiguity—is intentional and stylistically characteristic (Chernoff, 1979; Locke, 1982; 2009; 2010; Pressing, 2002). Others highlight the aspects of interweaving and integration of metric beat perception and cross-rhythmic accentuation into a rhythmically interesting, yet metrically unambiguous composite whole (Agawu, 1995; 2006; Nzewi, 1997; Burns, 2010). Importantly for the issue at hand, both views share the common factor that, for a meaningful perception of cross-rhythm, the ternary beat subdivision, equivalent to the eighth notes level in conventional 6/8 or 12/8 staff notation using dotted quarter notes for the beat level, is metrically functional.
| x | x | x | rhythmic onsets, ensemble part 1 | |||
| x | x | rhythmic onsets, ensemble part 2 | ||||
| x | x | x | x | resulting composite rhythm | ||
| ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | metric beat subdivision |
| ⋅ | ⋅ | ⋅ | hypothetical alternative beat, according to "metric ambiguity" interpretation | |||
| ⋅ | ⋅ | metric (main) beat | ||||
| ⋅ | metric cycle (6/8 measure) | |||||
Another rhythmic type, also characteristic of West African drumming, that suggests anchoring rhythmic accents to the fastest pulse can be found in the ostinatos that serve as so-called timelines, that is, as a listening reference for the coordination of ensemble polyrhythms. The rhythmic characteristic of many timelines is that they have onsets distributed asymmetrically yet with (near) maximal evenness across the metric cycle (Arom, 1984; Dauer, 1988; Toussaint, 2003; 2013; Agawu, 2006; Kubik, 2008). This typically involves a large number of onsets falling off the beat. For instance, the example of the often-studied timeline in Table 6 shows that five out of seven onsets fall on the off-beat. Given the function of the timeline as a quasi-metric listening reference for other ensemble members and audiences, it is implausible to assume that the majority of its accents would occur at a level of temporal resolution below the radar of metric perception.
| x | x | x | x | x | x | x | rhythmic onsets | |||||
| ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | 12-subdivision sub-cycle |
| ⋅ | ⋅ | ⋅ | ⋅ | metric beat | ||||||||
| ⋅ | metric cycle | |||||||||||
A fourth argument in support of the metrical relevance of the fastest pulse concerns motional patterns. Certain percussive playing techniques implement the fastest pulse by marking some or all of the unaccented time-points with a ghost-note. 5 The musicians thus anchor their timing in motional instantiations of the fastest pulse with their own bodies. The Malian jembe drummers who performed the recordings analyzed below (Case Study 2) frequently apply such motional patterns in their playing. Given that metric pulse perception in music and motion are closely linked in general (Phillips-Silver & Trainor, 2005; 2007) and in African music and dance in particular (Waterman, 1952; Blacking, 1971; Chernoff, 1979; Kauffman, 1980; Kubik, 1988; Locke, 1998), this supports the assumption of a metrical relevance of the targeted periodicity.
To conclude, it is a characteristic of the studied musical genres that rhythmic surfaces are (near) maximally saturated with continuous onset streams of definite periodicity. The present state of research on the perceptual and sensorimotor relevance of this fastest pulse is somewhat impaired by the fact that, first, no relevant laboratory experiments have been conducted in West Africa and second, metric perception and motor experience are not easily addressed by participant observation and music analysis, the methods typically applied in African music research. From everything we know, however, it would appear safe to assume that the saturated temporal framework of the fastest pulse is typically metrically relevant, as a "metric floor" (London, 2012) or "mental background pulsation" (Kubik, 1988; 1994; 2010) that helps anchor the higher levels of the metric hierarchy. While barely perceived consciously, the fact that this density referent indexes all structurally relevant time-points on the rhythmic surface will often enhance the timing and perception of African music. The fastest pulse in West African dance drumming thus arguably represents a relevant object for the study of the lower limit for meter. All of the recordings analyzed below are documents of live music performances for vernacular dance at public social celebrations. While the performing drummers are specialists, the functional context of the music allows us to assume that the measured subdivision durations correspond to the general population's metric skills.
CASE STUDY 1: EWE DRUMMING FROM SOUTHERN GHANA
Ewe is the name of a large and complex ethnic group from southeastern Ghana and Togo comprising over three million people altogether. Ewe drumming represents the best-researched repertoire of music from Africa (Jones, 1959; Koetting, 1970; Pantaleoni, 1972a; 1972b; 1972c; Chernoff, 1979; Locke, 1979; 1982; 1992; 1998; 2010; Agawu, 1995; 2006; Bareis, 1991; Burns, 2009). In the discursive development of scholarly concepts such as "West African percussion ensemble music," "dance drumming," "polyrhythm," "polymeter," "cross rhythm," and "African rhythm," Ewe drumming has served as the single most central point of reference. Of particular value for the present study is the high level of integration of music analysis, theory, ethnography, and documentary audio and video footage in the works of ethnomusicologists David Locke and James Burns (see Appendix 1 for a list of surveyed media). An explorative tempo analysis of excerpts (beginning, middle and end sections) of 30 recordings of five pieces (Gahu, Kinka, Slow Atsia, Fast Atsia, Kpegisu) can be summarized as follows.
The beat rates in Ewe drumming mostly range from 85 to 200 bpm (300–700 ms per beat). This is faster than the preferred beat tempo according to music psychology, which is 85–150 bpm or 400–700 ms per beat (Fraisse, 1982; Parncutt, 1994; Van Noorden & Moelants, 1999; Moelants, 2002). An especially notable tendency in Ewe music is to create maximally dense rhythmic surfaces by using higher subdivision cardinalities at the slower beat rates in an approximately negatively proportional relation. While the faster pieces with tempos around 200 bpm display a ternary beat subdivision for the most part, medium tempos (140–170 bpm) typically involve quaternary subdivisions, whereas a hexatolic (sextuplet) subdivision is often filled in to the relatively long beat IOIs at slower beat tempos around 100 bpm. This means that a major portion of the surveyed recordings features subdivision IOIs within a range of 90–120 ms. Evidently, the beat rate is not the single most important aspect defining the preferred tempo of Ewe drumming. Instead, the preference is for very fast subdivision rates, which occur relatively independent of the beat rate. The following analysis of subdivision cardinalities and intervals zooms in on Gahu, a piece to which Locke (1998) has dedicated an entire monograph entitled Drum Gahu.
Defining the fastest subdivision in Gahu
Based on ethnographic experience and music analysis, Locke (1998) posits a quaternary beat subdivision to represent the fastest metrically relevant periodicity in Gahu. This section discusses Locke's assumption and evaluates its plausibility compared to the alternative hypothesis of an 8-subcycle as the smallest metric subdivision.
The Ewe percussion ensemble for Gahu performances typically consists of at least six instruments: an iron double-bell (gankogui), a gourd rattle (axatse) and four drums, named kaganu, kidi, sogo, and boba (from high to low tuning). Each of these instruments performs a distinct musical role in the ensemble, which Locke theorizes as forming three groups. The role of the "time" instruments—bell, rattle, and kaganu—is to "articulate and embellish the key musical phrase which 'sculpts' time into a distinct 'shape' thereby implicitly establishing the music's meter" (Locke, 1998). The "response" drums—kaganu, kidi, and sogo—constitute a second layer of the polyrhythmic texture; they enjoy a certain space for variation which they use for interacting with the lead drum. The third layer consists of a single instrument, the highly variable lead drum called boba, whose many responsibilities include "setting the tempo, improvising on traditional phrases and providing choreographic signals" (Locke, 1998).
The bell plays an asymmetric ostinato that functions as a timeline pattern. The rhythmic figure often used for Gahu spans across four beats and sixteen subdivisions. However, in the recordings measured below, a simpler form of the bell pattern, with a length of only two beats and eight subdivisions, is used; the IOIs of its three strokes display a ratio of 3:3:2 (see notational Table 7). Several rattles (axatses), which are very loud, accompany the bell. The drum kaganu, which supports both the time and the response layers of the ensemble, performs a simple and strictly invariant, fully off-beat ostinato that repeats in each beat. The basic kidi phrase is more complex: it contains two slightly different motives of two beats length which combine to form a relatively off-beat four-beat phrase. The basic phrase for the response drum sogo is even simpler and more beat-oriented, spanning only two beats. While the kidi and sogo drum players can draw on a certain pool of more or less complex phrases for improvisatory variation, the range and significance of expressive variability characteristic of the musical role of the lead drum boba is tremendous. Locke dedicates a chapter of over 50 pages and dozens of musical examples to the analysis of various standard phrases and inherent conventional procedures for developing variations, embellishments, musical periods, and form parts by sequencing phrases and variations. The example shown in the chart is a version of the most basic, or "ancestral" lead drum phrase for boba.
| x | x | x | x | x | x | bell | ||||||||||
| x | x | x | x | x | x | x | x | rattle | ||||||||
| O | O | O | O | O | O | O | O | kaganu drum | ||||||||
| O | O | o | o | O | O | O | O | o | o | O | O | kidi drum | ||||
| o | O | o | o | O | o | sogo drum | ||||||||||
| O | O | O | O | o | o | O | O | O | o | o | boba (lead) drum | |||||
| • | • | • | • | • | • | • | • | • | • | • | • | • | • | • | • | 16-subdivision sub-cycle |
| • | • | • | • | • | • | • | • | 8-subdivision sub-cycle | ||||||||
| • | • | • | • | beat | ||||||||||||
| • | cycle | |||||||||||||||
The above table shows a continuous stream of sixteen onsets emerging from the composite ensemble polyrhythm for Gahu, which supports Locke's assumption of a 4-beat/16-subdivision meter. The rhythmic structures of some of the individual phrases can hardly be understood as metrically based on the hypothetical alternative 8-subdivision. For instance, one out of three strokes of the ostinato bell pattern (the one right before Beat 2 and Beat 4, respectively) falls midway between instantiations of the 8-subdivision. The off-beat position of this stroke is constitutive of the rhythmic asymmetry, and thus of the core structural characteristic of that timeline. Whether conceived of as integrated into a 3:3:2 rhythmic figure or as an upbeat anchored to the following beat (syncopation), that stroke depends on the quaternary subdivision as a level of metric density. A second aspect that calls for a metrical conception of the 16-subdivision cycle is the strikingly complex polyrhythmic coordination of the simultaneously played phrases of the six ensemble parts. For instance, the rhythms of the response drums "are designed to mesh together like gears in a finely-tooled engine" (Locke, 1998, p. 46). The radically off-beat kaganu, the relatively of-beat kidi, and the beat-oriented sogo drum patterns contrast starkly in their different relations to higher metric levels and relate to each other in a strongly interlocking fashion; when performed together, they produce a characteristic melody (see Table 8). In order to allow for the precise timing necessary for this to occur in a seamlessly interwoven flow, shared entrainment to a common density referent is a prerequisite.
| O | O | O | O | kaganu drum | ||||
| O | O | O | O | kidi drum | ||||
| O | sogo drum | |||||||
| O | O | O | O | O | O | O | resulting melo-rhythm | |
| • | • | • | • | • | • | • | • | quaternary subdivision |
| • | • | beat | ||||||
| • | cycle | |||||||
In summary, the 16-subdivision sub-cycle, which represents the correlate of the fastest onset stream at the rhythmic surface level, serves as a density referent that anchors the metrical hierarchy. We can thus calculate the shortest metrically relevant subdivision in Gahu as the measured IOIs of the 4-beat cycle divided by the factor 16.
Measuring the fastest subdivision in Gahu
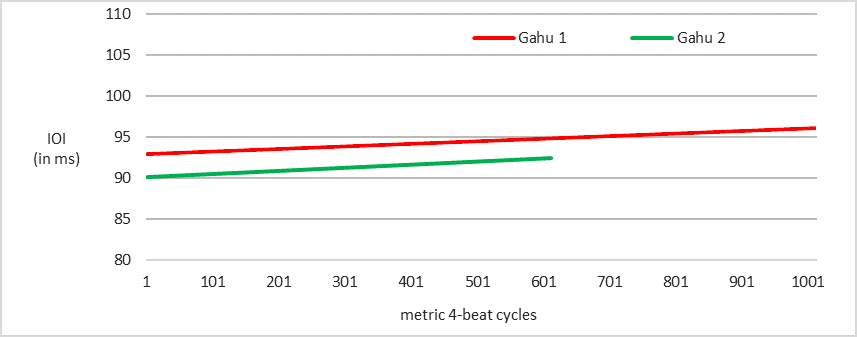
This section analyzes two fairly lengthy Gahu performances by Godwin Agbeli and the Kopeyia village community, both of which were recorded and published by Locke (1994). The first one, Gahu 1, has a running time of 25:40 minutes and features 1,015 metric cycles. The second one, Gahu 2, spans 15 minutes and covers 612 metric cycles.
According to Locke (1998), Gahu performances typically involve tempos of approximately 138–168 bpm. Timing measurements of the two recordings show tempos between 150 and 170 bpm, thus verifying Locke's specification of the upper tempo limit. Accordingly, subdivision durations preponderantly range from about 88 to 100 ms. The mean subdivision IOI is 95 ms in Gahu 1 and 91 ms in Gahu 2. There are several subsequent waves of very slight tempo changes in each performance, which range from about 90 to 100 ms in Gahu 1 and from about 90 to 95 ms in Gahu 2 (see Figure 3-A). A minimal increase of the durations (decrease of tempo) occurs over the course of the recordings (see Figure 3-B). I divided both recordings into two parts, each with the same amount of measured cycles, and found a difference of no more than 1 ms between the mean values for the first and second halves to be statistically significant: 94 ms versus 95 ms in Gahu 1 [t(996) = -5.860, p < .001] and 91 ms versus 92 ms in Gahu 2 [t(610) = -5.363, p < .001]. In view of the long running times of the performances (15–25 min), this minuscule variation in the subdivision durations testifies to an amazing stability in the overall tempo performance.
CASE STUDY 2: JEMBE DRUMMING FROM MALI
The jembe is a goblet shaped drum, played with bare hands, originating from Guinea and Mali. Alternative spellings include jenbe (Mali), dyembe (Guinea), and djembé (French). Jembe-centered percussion ensemble music has traditionally enlivened local dance events. In the 1960s, jembe music and dance entered the programs of state-sponsored folklore ensembles and, at the same time, became part of urban popular culture in the rapidly growing cities of Bamako, Conakry, Dakar, and Abidjan, among others. Since the 1980s, West African jembe music, musicians, and instruments have migrated globally (Charry, 2000; Polak, 2000). The corpus of media under scrutiny is taken from a private research archive of audio and video recordings produced by the author in Mali over ten periods of fieldwork between 1991 and 2012 (yielding over 40 hours of recordings), plus one hour of video footage shot by Charry in 1990.
Jembe-centric dance music ensembles usually consist of one to three jembes plus one to three dunduns. The dundun is a mid- to low-tuned cylindrical drum with a skin at both ends, played with one stick. The corpus studied here features mainly trios (Jembe 1 = lead drum; Jembe 2 = ostinato accompaniment; Dundun 1 = timeline) and quartets (Dundun 2 = further ostinato accompaniment), as is typical of the Bamako style of jembe music performance in the 1990s and early 2000s (see Polak, 2004). The criterion for selecting pieces of repertoire for survey was popularity. The five chosen pieces, Maraka, Dansa, Suku, Kirin, and Madan, are the ones most frequently performed at vernacular social dance celebrations in Bamako (see Polak, 2012).
A survey of twenty-five recordings revealed a radically different approach to tempo from the one followed by Ewe drummers and dancers. Whereas in southern Ghana the tempo is, for the most part, very stable, a structural, often nearly continuous accelerando characterizes each dance-drum performance in southern Mali. Depending on piece and performance context, intermittent stepwise accelerandos also occur frequently. Many performances consist of two sections: first, a slower one including singing and a solemn group dance and second, a faster one featuring short and highly energetic individual dance solos (see Polak, 2007), with a sharp increase in tempo at the intersection between the two parts. Some pieces arrange the two-part form by switching from one ensemble rhythm covering the first section to another one dedicated to the faster tempos of the second one. Others cover the full range of performed tempos with basically the same polyrhythm.
Detailed measurements of twelve full performances resulted in beat tempos ranging from 70 to 125 bpm at the beginning of pieces and from 180 and 240 bpm at the end. The tempo increases by 65–200 percent in the course of each performance, even though the pieces often last no longer than a few minutes. It is thus obvious that no specific tempo can characterize jembe music performance as a "preferred" tempo. Instead, a constant acceleration constitutes the normal mode and a characteristic quality of performing the music. Acceleration represents a core factor in the aesthetics of rhythm and tempo not only in jembe music, but in Malian dance drumming in general (cf. Polak & London, 2014). Since acceleration cannot go on forever within the context of a stable metric hierarchy, jembe music performance presents a particularly interesting case for studying the lower limit for meter.
For the sake of simple analysis, the pieces selected for closer inspection (Kirin and Maraka; see Table 9) are similar to one another in terms of rhythmic structure and neither displays transformations of the metric structure at the intersections between the slower and faster parts.
| Item | running time | metric cycles | Source | Recording | Ensemble leader |
|---|---|---|---|---|---|
| Kirin 1 | 2:45 | 110 | archive R. Polak | 1994 | Jaraba Jakite |
| Kirin 2 | 2:00 | 85 | archive R. Polak | 2006 | Drissa Kone |
| Kirin 3 | 3:00 | 115 | archive R. Polak | 2000 | Drissa Kone |
| Kirin 4 | 4:10 | 155 | archive R. Polak | 2012 | Sedu Balo |
| Maraka 1 | 3:55 | 195 | archive R. Polak | 2006 | Sedu Balo |
| Maraka 2 | 4:00 | 175 | archive E. Charry | 1990 | Drissa Kone |
| Maraka 3 | 3:20 | 140 | archive R. Polak | 2006 | Jeli Madi Kuyate |
| Maraka 4 | 3:50 | 210 | archive R. Polak | 1997 | Jaraba Jakite |
Defining the fastest subdivision in Kirin
The piece Kirin (also spelled N'gri, or called Wasulunka) displays a 4-beat/12-subdivision metric type (cf. Polak, 2010), which is allocated either a 12/8 or a 6/8 time-signature by authors using Western staff notation (Locke, 1979; 1982; Anku,1988; 2000; Agawu, 2006). Table 9 shows the ensemble texture for Kirin. Dundun 1 provides the timeline in Malian jembe music; the rhythmic figure of the timeline for Kirin is identical to what is addressed as the "standard pattern" in the study of Ewe music (Jones, 1959; Agawu, 2006) and was given as an example for asymmetric timelines above (see Table 6). In the fastest sections of Kirin performances, dundun drummers tend to leave out two of the seven strokes of the timeline-rhythm, which makes the pattern technically easier to play (remember that dundun players use only one stick to beat the drum), while leaving the basic asymmetric structure intact. Dundun 2 performs an accompaniment part that consists of playing out the beat. The phrase for Jembe 1, the variable lead drum, consists of two motives: a beat-oriented one on Beats 1 and 2 and a second one that, expanding on the timeline, proceeds from a highly characteristic accentuation of the second subdivision (the first of the two off-beat positions) of Beat 3 to metric stability on Beat 4. Jembe 2 contributes a second accompanying ostinato, the cross-rhythmic figure of which contrasts starkly with the on-beat pattern of Dundun 2.
| O | o | O | O | o | o | O | Dundun 1 (full pattern) | |||||
| O | O | O | o | o | Dundun 1 (reduced pattern) | |||||||
| O | O | O | O | Dundun 2 | ||||||||
| B | S | S | B | B | T | T | T | B | Jembe 1 | |||
| S | S | T | T | S | S | T | T | Jembe 2 | ||||
| • | • | • | • | • | • | • | • | • | • | • | • | 12-subdivision cycle |
| • | • | • | • | beat | ||||||||
| • | cycle | |||||||||||
The fastest continuous stream of onsets in Kirin evidently takes place at the level of the 12-subdivision, or ternary subdivision of the beat. Both the cross-rhythmic pattern of Jembe 2 and the asymmetric rhythm of Dundun 1 rely fundamentally on off-beat strokes. Their rhythms would be very hard to perform, and to entrain to by listeners, particularly at fast tempos, without the off-beats being anchored to a regular subdivision. Concerning inter-part coordination, the relationships between Jembe 2 and Dundun 2, between Dundun 1 and Dundun 2, or (in Beats 3 and 4) between Jembe 2 and Dundun 1, are characterized by many interlocking accents.
To conclude, the 12-subdivision cycle functions as a density referent for anchoring the metric hierarchy in Kirin. The fastest metrically relevant subdivision in Kirin performances can thus be calculated as the 4-beat cycle duration divided by the factor 12.
Subdivision IOIs in Kirin
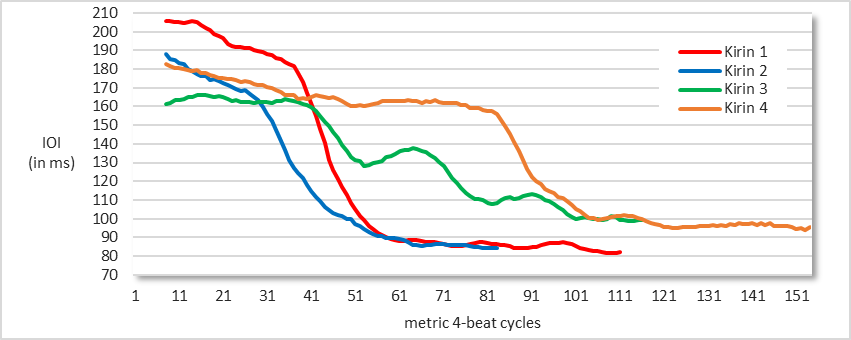
Each of the four measured performances of Kirin features a drastic increase in tempo which appears to be nearly continuous in some sections and is more marked in others. The tempo is relatively stable only in the final and fastest section of each recording. In these fastest periods, subdivision IOIs range from about 85 to 90 ms in Kirin 1 and 2, and from about 95 to 105 ms in Kirin 3 and 4 (see Figure 4).
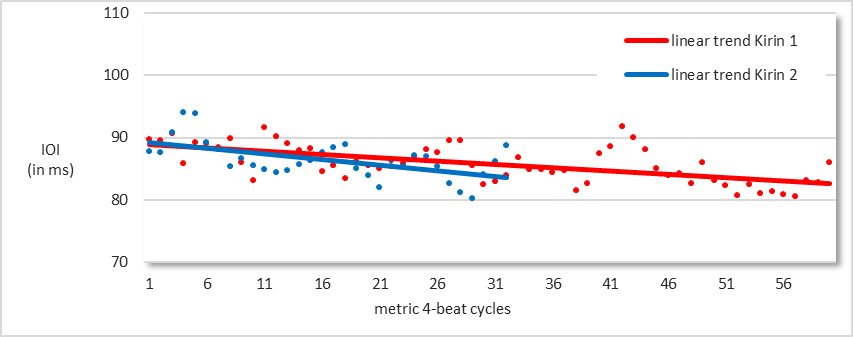
The average subdivision IOI across the fastest sections both in Kirin 1 (final 60 cycles) and Kirin 2 (final 32 cycles) is 86 ms. A slight trend towards further acceleration is still evident even during these extremely rapid sections (see Figure 5). I divided these final sections into two parts and found a very small, yet statistically significant difference between the first and second halves: 87 ms versus 84 ms [t(56) = 4.501, p < .001] in Kirin 1 and 88 ms versus 85 ms in Kirin 2 [t(30) = 2.666, p = .012].
The fastest subdivision in Maraka
Table 11 presents the basic polyrhythm for Maraka (also called Maraka-Dòn or Denba-Fòli), which combines an asymmetric timeline (Dundun 1) with both cross-rhythmic (Dundun 2) and beat-oriented (Jembe 2) ostinatos for accompaniment, and a highly off-beat lead drum phrase (Jembe 1).
| O | o | o | O | O | O | Dundun 1 (full pattern) | ||||||
| O | o | O | O | Dundun 1 (reduced pattern) | ||||||||
| O | O | O | O | Dundun 2 | ||||||||
| B | S | T | T | S | B | S | B | S | Jembe 1 | |||
| S | T | S | B | S | T | S | B | Jembe 2 | ||||
| • | • | • | • | • | • | • | • | • | • | • | • | 12-subdivision sub-cycle |
| • | • | • | • | beat | ||||||||
| • | cycle | |||||||||||
The timeline (Dundun 1) for Maraka has four off-beat versus two on-beat strokes in its full pattern. When performing the reduced version of the pattern, many players maintain the original rhythm by substituting the omitted strokes with time-keeping ghost-notes performed by the weak hand. As a rule, dundun players use the stroke on subdivision 2 of beat 3 as a point of entry when taking up the rhythm at the beginning of a piece or after some variation or break. Timing this entry precisely in a merely beat-based metric context without a nested subdivision framework would be difficult.
Concerning the polyrhythmic coordination, a consistent interlocking of displaced accents marks the relations between various ensemble parts, particularly in beats 3 and 4, for instance between Jembe 1 and Jembe 2 and between Dundun 1 and Dundun 2. The fluent interweaving and integrated listening of such polyrhythmic interlocking indicates a shared entrainment to the 12-subdivision.
In summary, the (poly-)rhythmic structure of the piece Maraka clearly requires metric beat subdivision. As in the case of Kirin, one can thus calculate the IOIs of the fastest metrically relevant pulse in Maraka as the duration of the 4-beat cycle divided by the factor 12.
Subdivision IOIs in Maraka
All measured recordings of Maraka display enormous accelerandos. Again, tempos are only relatively stable in the final sections of each performance. In these extremely rapid sections, subdivision IOIs range from about 90–110 ms in recordings Maraka 2 and 3, and decrease to 80–90 ms in Maraka 1 and 4 (see Figure 6).
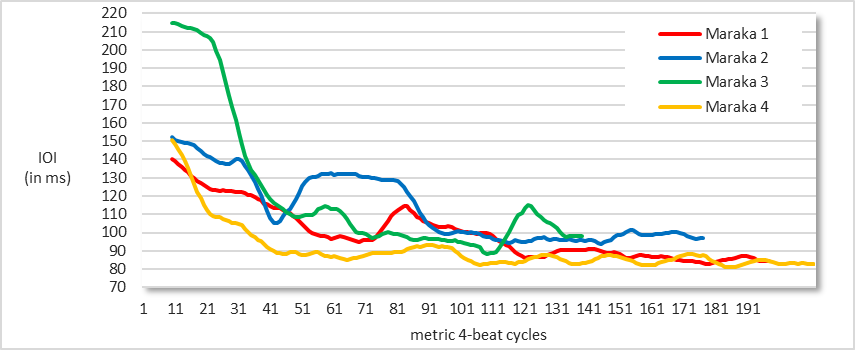
Fig. 6. Subdivision IOIs (moving mean, averaged across eight cycles) in four performances of Maraka.
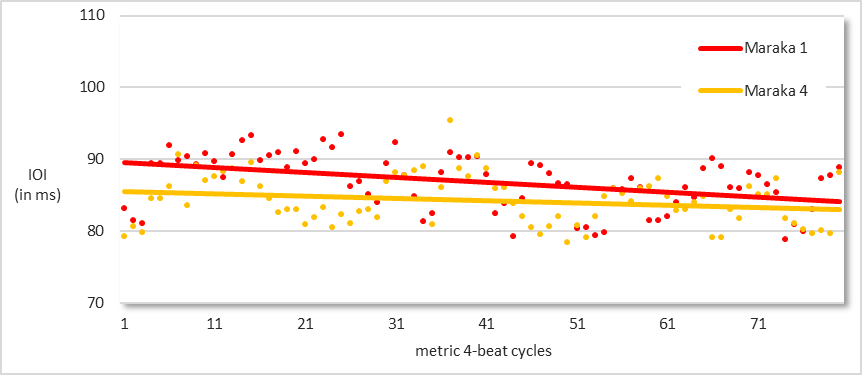
Fig. 7. Linear trend of subdivision IOIs (in ms) in the final section (last 80 metric cycles) of two performances of Maraka.
Figure 7 shows the last 80 metric cycles of the two fastest recordings. The average subdivision IOI across this period is 87 ms in Maraka 1 and 84 ms in Maraka 4. Again, a slight trend towards further increases in tempo is observable even in these extremely rapid sections. A comparison between the first and last 40 cycles within the final 80-cycle sections results in small yet statistically significant differences: 89 ms versus 85 ms in Maraka 1 [t(78) = 4.925, p < .001] and 85 ms versus 83 ms in Maraka 4 [t(74) = 3.017, p = .004].
DISCUSSION
Ghanaian drummers, listeners, and dancers maintain subdivisions as short as 90–100 ms for extended periods of time in the context of performances of the popular piece Gahu. The tempo is extremely stable overall, yet shows small fluctuations and a minuscule trend towards decreasing over the course of performances. One might speculate that the demonstrated decrease in tempo, however minimal, indicates that performing near the lower limit for meter already acts as a slight constraint on the aesthetic desire for a stable tempo.
In Malian jembe drumming for public dance events, near continuous tempo acceleration is characteristic of performance practice. Near the end of the pieces, drummers often push the tempo literally as far as they can. During these sections, subdivision intervals between 80 and 100 milliseconds are common. IOIs frequently go below 90 ms, yet hardly below 80 ms (Fig. 4–7). A threshold range of about 80–100 ms for subdivision durations evidently represents the lower limit for meter in jembe music performance, and probably in West African drumming in general.
As the drummers can play considerably shorter durations (e.g., in extensively ornamented sections), the constraint appears to be perceptual rather than motor-driven on their part. The recordings analyzed feature vernacular dance music. It may be that tempo constraints on the dancers' movement patterns contribute to the limit for metric subdivisions. However, many jembe pieces display a two-part form with quaternary subdivision in the first section and ternary in the second, or ternary subdivision in the first section and binary in the second, respectively. In these pieces, the dancers use the reduction of the subdivision cardinality in the drumming to push the beat rate further. This suggests that it is indeed auditory perception that constrains the subdivision duration rather than the dancers' motion patterns. As said, however, I cannot rule out that dance motion and perhaps other factors not considered here contribute to the constraint.
It may be tempting to interpret the empirical evidence on the shortest durations that occur in performance practice (about 80 ms) as a relatively hard lower limit for meter. However, the experimental studies discussed in the "Background" section suggested that the lower limit for meter subjects subdivision durations to perceptual constraints on a gradual, rather than a clear-cut basis. Instead of a single hard limit, I therefore propose that we estimate a range of durations within which the soft constraint can be expected to exert a strong influence. That range is about 80–100 ms for the music studied here (West African drumming) and corresponds almost exactly to the shortest subdivision durations in jazz performance and East African xylophone playing, as discussed above. While American jazz, West African drumming, and East African xylophone music are historically and geographically different styles of music, they share a preference for very dense and driving surface rhythms with note onsets articulated precisely by percussive sounds. These styles and the correspondingly experienced communities of listeners may constitute optimal contexts for extremely short metric subdivisions. I propose that the hypothetical 80–100 ms range apparently valid for African and African-diasporic music represents the lower end of a universal, yet culturally, stylistically, and individually contingent constraint. There are many styles of music that may perhaps use subdivisions that are just as rapid, for instance virtuoso violin playing in European classical and folk musics, bluegrass banjo, shred metal, flamenco guitar playing, Hindustani and Carnatic drumming from India, Afro-Brasilian samba, Cuban rumba columbia, and electronic dance music genres such as jungle. 6 However, I predict that there will rarely be much space for venturing far below 80 ms in rhythms intended to afford metric entrainment for general audiences.
The proposition of an 80–100 ms threshold range for performed music contrasts with Repp's (2003) finding of a soft 100–120 ms lower limit for the task of sensori-motor synchronization in laboratory experiments (tapping along with audio stimuli). This difference may result from the fact that the interesting musical arrangement of different pitches, timbres, intensities, and rhythmic figurations characteristic of human music performance, facilitates faster metric subdivisions than the dead-pan isochronous equitones used in laboratory experiments, as Repp (2003, 361) suggested.
This paper focused on the lower durational limit for metric subdivision, while also permitting a few glimpses into other aspects of musical rhythm and tempo. Ewe drumming from Ghana privileges stable tempos and a specific range of subdivision intervals (90–120 ms) independently of the beat rate. This resonates with London's suggestion that the apprehension of tempo is more complex than assumed by the conventional, one-dimensional equation of tempo with the beat rate, and that event density and subdivision rate are highly relevant factors (London 2011). In jembe music from Mali, the preferred quality of tempo appears to lie not in any beat or subdivision rate at all, but rather in the very process of acceleration, including the climactic experience of meeting its limit. These contrasting approaches to musical tempo in two West African musical cultures serve to remind us of the vast cultural diversity in human rhythm production, even within what is often subsumed under the single concept "African rhythm." A possible interaction between this diversity of musical behavior and aspects of perception, cognition and aesthetics should provide an interesting subject for future empirical study.
ACKNOWLEDGEMENTS
The research was generously funded by the Hochschule für Musik und Tanz Köln. Ethnomusicologists Eric Charry, David Locke, James Burns, and Andreas Meyer collegially provided unpublished audio-visual documents of their ethnographic fieldwork. Andreas Meyer, Justin London, and Anders Friberg commented on drafts and offered very valuable suggestions for improving the arguments. Proof-reading by Michi Henning and Nicola Heine helped to reduce grammatical mistakes and torturous formulations. Thank you all! This article was copyedited by Dana Lauren DeVlieger and layout edited by Kelly Jakubowski.
NOTES
- The author's affiliation changed from Hochschule für Musik und Tanz Köln to Max Planck Institute for Empirical Aesthetics (Frankfurt a.M.) during the publication process. Correspondence can be addressed to rainer.polak@ae.mpg.de.
Return to Text - Listen to Kubik (1994-accompanying CD, tracks # 2, 3, and 5) and Cooke & Wachsmann (2003-CD, tracks # 2, 3, and 10).
Return to Text - The repertoires I surveyed and found to feature less rapid subdivision rates include Khasonka (Khassonké) and Bamana (Bambara) drumming from western and central Mali (cf. Polak & London, 2014), Asante (Akan) percussion from southwestern Ghana (cf. Meyer 2005), and Dagomba (Dagbani) music from northern Ghana (cf. Locke, 1990).
Return to Text - In some repertoires of West African drumming, the subdivision is non-isochronous, i.e., beat subdivision is structured according to stable periodic patterns of distinct subdivision classes (Polak, 2010; Polak & London, 2014; Polak, London, & Jacoby, 2016). For instance, the jembe piece Manjanin displays a recurrent short-medium-long pattern of the ternary beat subdivision, with the short intervals, but not the medium and long ones, frequently being as short as 80–90 ms (Polak, 2010, Tables 2, 5, and 7; endnote 45).
Return to Text - Ghost-notes do not feature a specific melodic value or timbre, but precise motor-timing. From the performer's perspective, they appear to be integrated into the flow of rhythmic figure, the effort-saving maintenance of which is their very function. Malian jembe players often design hand-patterns for accented strokes so as to allow for minute motional representations of all non-accented subdivision positions ("rests"). Dundun players often perform ghost notes with their weaker hand (the left hand for right-handers), while the stronger hand performs all accented strokes.
Return to Text - I would like to thank Fernando Benadon, Justin London, and Michi Henning for independently suggesting this point.
Return to Text
REFERENCES
- Agawu, K. (1995). African rhythm: A Northern Ewe perspective. Cambridge: Cambridge University Press.
- Agawu, K. (2003). Representing African music: Postcolonial notes, queries, positions. New York: Routledge.
- Agawu, K. (2006). Structural analysis or cultural analysis? Competing perspectives on the 'standard pattern' of West African rhythm. Journal of the American Musicological Society, 59(1), 1-46. https://doi.org/10.1525/jams.2006.59.1.1
- Anku, W. O. (1988). Procedures in African drumming: A study of Akan/Ewe traditions and African drumming in Pittsburg. PhD diss., University of Pittsburgh, USA.
- Anku, W. O. (2000). Circles and time: A theory of structural organization of rhythm in African music. Music Theory Online, 6(1).
- Arom, S. (1984). Structuration du Temps dans les Musiques d'Afrique Centrale. Revue de Musicologie, 70(1), 5-36. https://doi.org/10.2307/928652
- Bareis, U. (1991). Formen neo-traditioneller Musik in Kpando, Ghana. In: V. Erlmann (Ed.), Populäre Musik in Afrika (pp. 59-108). Berlin: Staatliche Museen Preussischer Kulturbesitz.
- Blacking, J. (1967). Venda children's songs: A study in ethnomusicological analysis. Chicago: University of Chicago Press.
- Blacking, J. (1971). Deep and surface structures in Venda music. Yearbook of the International Folk Music Council, 3, 91-108. https://doi.org/10.2307/767458
- Burns, J. (2009). Female voices from an Ewe dance-drumming community in Ghana: Our music has become a divine spirit. Burlington, VT: Ashgate.
- Burns, J. (2010). Rhythmic archetypes in instrumental music from Africa and the diaspora. Music Theory Online, 16(4).
- Charry, E. (2000). Mande music: Traditional and modern music of the Maninka and Mandinka of Western Africa. Chicago: University of Chicago Press.
- Chernoff, J. M. (1979). African rhythm and African sensibility: Aesthetics and social action in African musical idioms. Chicago: University of Chicago Press.
- Clayton, M. (1997). Le metre et le tal dans la musique de l'Inde du Nord. Cahiers de musiques traditionnelles, 10, 169-189. https://doi.org/10.2307/40240271
- Collier, G., & Collier, J. L. (1994). An exploration of the use of tempo in jazz. Music Perception, 11, 219-242. https://doi.org/10.2307/40285621
- Cooke, P. (1970). Ganda xylophone music: Another approach. African Music, 4(4), 62-95. https://doi.org/10.21504/amj.v4i4.1682
- Cooke, P., & Wachsmann, K. (Coll./Ed.) (2003-CD) The king's musicians. Royalist music of Buganda Uganda. British Library Sound Archive, Topic Records TSCD925.
- Dauer, A. M. (1966). Afrikanische Musik und völkerkundlicher Tonfilm. Ein Beitrag zur Methodik der Transkription. Research Film, 5, 439-456.
- Dauer, A. M. (1988). Derler 1. Ein System zur Klassifikation von Rhythmen. Musiktheoretische und musikhistorische Aspekte. Jazzforschung / Jazz Research, 20, 117-154.
- Dittmar, C., Pfleiderer, M., & Müller, M. (2015). Automated estimation of ride cymbal swing ratios in jazz recordings. In M. Müller & F. Wiering (Eds.), Proceedings of the 16th International Society for Music Information Retrieval Conference (ISMIR), Málaga, Spain (pp. 272–277).
- Drake, C., Penel, A., & Bigand, E. (2000). Tapping in time with mechanically and expressively performed music. Music Perception, 18(1), 1–24. https://doi.org/10.2307/40285899
- Fraisse, P. (1982). Rhythm and tempo. In: D. Deutsch (Ed.), The psychology of music (pp. 149-180). New York: Academic Press. https://doi.org/10.1016/B978-0-12-213562-0.50010-3
- Friberg, A., & Sundström, A. (2002). Swing ratios and ensemble timing in jazz performance: Evidence for a common rhythmic pattern. Music Perception, 19(3), 333-349. https://doi.org/10.1525/mp.2002.19.3.333
- Handel, S. (1991). Listening: An introduction to the perception of auditory events. Cambridge, MA: MIT Press.
- Henrich, J., Heine, S. J., & Norenzayan, A. (2010). The weirdest people in the world? Behavioral and Brain Sciences, 33(2-3), 61–83. https://doi.org/10.1017/S0140525X0999152X
- Jones, A. M. (1959). Studies in African music. London: Oxford University Press.
- Kauffman, R. (1980). African rhythm: A reassessment. Ethnomusicology, 24(3), 393-415. https://doi.org/10.2307/851150
- Koetting, J. (1970). The analysis and notation of West African drum ensemble music. Selected Reports in Ethnomusicology, 1(3), 116-146.
- Kolinski, M. (1973). A cross-cultural approach to metro-rhythmic patterns. Ethnomusicology, 17(3), 494-506. https://doi.org/10.2307/849962
- Krebs, H. (1999). Fantasy pieces: Metrical dissonance in the music of Robert Schumann. Oxford: Oxford University Press. https://doi.org/10.1093/acprof:oso/9780195116236.001.0001
- Kubik, G. (1969). Composition techniques in Kiganda xylophone music: With an introduction into some Kiganda musical concepts. African Music, 4(3), 22-72. https://doi.org/10.21504/amj.v4i3.1437
- Kubik, G. (1988). Einige Grundbegriffe und -konzepte der Afrikanischen Musikforschung. In: G. Kubik, Zum Verstehen Afrikanischer Musik (pp. 52-113). Leipzig: Reclam.
- Kubik, G. (1994). Theory of African Music, Volume I. Wilhelmshaven: Florian Noetzel.
- Kubik, G. (2008). Zur Mathematik und Geschichte der afrikanischen time-line Formeln. In: A. Schneider (Ed.), Systematic and Comparative Musicology: Concepts, Methods, Findings (pp. 359-398). Frankfurt am Main: Peter Lang.
- Kubik, G. (2010). Theory of African Music, Volume II. Chicago: The University of Chicago Press.
- Lerdahl, F., & Jackendoff, R. (1983). A generative theory of tonal music. Cambridge, Mass.: MIT Press.
- Locke, D. (1979). The music of Atsiagbeko. PhD diss., Wesleyan University, USA.
- Locke, D. (1982). Principles of off-beat timing and cross-rhythm in Southern Eve dance drumming. Ethnomusicology, 26(2), 217-46. https://doi.org/10.2307/851524
- Locke, D. (1990). Drum Damba: Talking drum lessons. Crown Point, Indiana: White Cliffs Media.
- Locke, D. (1992). Kpegisu: A war d rum of the Ewe. Tempe, AZ: White Cliffs Media.
- Locke, D. (1998). Drum Gahu: An Introduction to African Rhythm. Tempe, AZ: White Cliffs Media.
- Locke, D. (2009). Simultaneous multidimensionality in African music. African Music, 8(3), 8-37. https://doi.org/10.21504/amj.v8i3.1826
- Locke, D. (2010). Yewevu in the metric matrix. Music Theory Online, 16(4).
- London, J. (2002): Cognitive constraints on metric systems: Some observations and hypotheses. In: Music Perception, 19, 529-550. https://doi.org/10.1525/mp.2002.19.4.529
- London, J. (2011). Tactus ≠ tempo: Some dissociations between attentional focus, motor behavior, and tempo judgment. Empirical Musicology Review, 6(1), 43-55. https://doi.org/10.18061/1811/49761
- London, J. (2012). Hearing in time: Psychological aspects of musical meter (2. ed.). Oxford: Oxford University Press. https://doi.org/10.1093/acprof:oso/9780199744374.001.0001
- London, J., Polak, R., & Jacoby, N. (2017). Rhythm histograms and musical meter: A corpus study of Malian percussion music. Psychonomic Bulletin & Review, 24(2), 474–480. https://doi.org/10.3758/s13423-016-1093-7
- McAuley, J. D. (2010). Tempo and rhythm. In M. Riess Jones, R. R. Fay, & A. N. Popper (Eds.), Springer Handbook of Auditory Research. Music Perception (Vol. 36, pp. 165–199). New York, NY: Springer New York. https://doi.org/10.1007/978-1-4419-6114-3_6
- McAuley, J. D., Jones, M. R., Holub, S., Johnston, H. M., & Miller, N. S. (2006). The time of our lives: Lifespan development of timing and event tracking. Journal of Experimental Psychology. General, 135(3), 348–367. https://doi.org/10.1037/0096-3445.135.3.348
- Meyer, A. (2005). Überlieferung, Individualität und musikalische Interaktion. Neuere Formen der Ensemblemusik in Asante/Ghana. Frankfurt: Peter Lang.
- Micklem, J., Cooke, A., & Stone, M. (1999). Xylophone music of Uganda: The Embaire of Nakibembe, Busoga. African Music, 7(4), 29-46.
- Mirka, D. (2009). Metric manipulations in Haydn and Mozart: Chamber music for strings, 1787-1791. New York: Oxford University Press. https://doi.org/10.1093/acprof:oso/9780195384925.001.0001
- Moelants, D. (2002). Preferred tempo reconsidered. In: C. Stevens, D. Burnham, G. McPherson, E. Schubert, & J. Renwick (Eds.), Proceedings of the 7th International Conference on Music Perception and Cognition (pp. 580-583). Adelaide: Causal Productions.
- Nketia, J. K. (1963). Folk songs of Ghana. Legon: University of Ghana.
- Nzewi, M. E. (1997). African music: Theoretical content and creative continuum. The culture-exponent's definitions. Oldershausen: Institut für Didaktik populärer Musik.
- Pantaleoni, H. (1972a). Toward understanding the play of sogo in Atsia. Ethnomusicology, 16(1), 1-37. https://doi.org/10.2307/850441
- Pantaleoni, H. (1972b). Toward understanding the play of atsimevu in Atsia. African Music, 5(2), 64-84. https://doi.org/10.21504/amj.v5i2.1420
- Pantaleoni, H. (1972c). Three principles of timing in anlo Drumming. African Music, 5(2), 50-63. https://doi.org/10.21504/amj.v5i2.1419
- Parncutt, R. (1994). A perceptual model of pulse salience and metrical accent in musical rhythms. Music Perception, 11(4), 409-464. https://doi.org/10.2307/40285633
- Phillips-Silver, J., & Trainor, L. J. (2005). Feeling the beat: Movement influences infants' rhythm perception. Science, 308, 1430. https://doi.org/10.1126/science.1110922
- Phillips-Silver, J., & Trainor, L. J. (2007). Hearing what the body feels: Auditory encoding of rhythmic movement. Cognition, 105(3), 533-546. https://doi.org/10.1016/j.cognition.2006.11.006
- Polak, R. (2000). A Musical instrument travels around the world: Jembe playing in Bamako, in West Africa, and beyond. The World of Music, 42(3), 7-46.
- Polak, R. (2004). Festmusik als Arbeit, Trommeln als Beruf. Jenbe-Spieler in einer westafrikanischen Großstadt. Berlin: Reimer.
- Polak, R. (2007). Performing audience: On the social constitution of focused interaction at celebrations in Mali. Anthropos, 102(1), 3-18.
- Polak, R. (2010). Rhythmic feel as meter: Non-isochronous beat subdivision in jembe music from Mali. Music Theory Online, 16(4).
- Polak, R. (2012). Urban drumming: Traditional celebration music in a West African city (Bamako). In: E. Charry (Ed.) Hip hop Africa: New African music in a globalizing world (pp. 261-281). Bloomington: Indiana University Press.
- Polak, R., & London, J. (2014). Timing and meter in Mande drumming from Mali. Music Theory Online, 20(1).
- Polak, R., Jacoby, N., & London, J. (2016). Both isochronous and non-isochronous metrical subdivision afford precise and stable ensemble entrainment: A corpus study of Malian jembe drumming. Frontiers in Neuroscience, 10, 285. https://doi.org/10.3389/fnins.2016.00285
- Pressing, J. (2002). Black Atlantic rhythm: Its computational and transcultural foundations. Music Perception, 19(3), 285-310. https://doi.org/10.1525/mp.2002.19.3.285
- Repp, B. H. (2003). Rate limits in sensorimotor synchronization with auditory and visual sequences: The synchronization threshold and the benefits and costs of interval subdivision. Journal of Motor Behavior, 35(4), 355-370. https://doi.org/10.1080/00222890309603156
- Repp, B. H. (2005a). Rate limits of on-beat and off-beat tapping with simple auditory rhythms: 1. Qualitative observations. Music Perception, 22(3), 479–496. https://doi.org/10.1525/mp.2005.22.3.479
- Repp, B. H. (2005b). Rate limits of on-beat and off-beat tapping with simple auditory rhythms: 2. The roles of different kinds of accent. Music Perception, 23(2), 165–188. https://doi.org/10.1525/mp.2005.23.2.165
- Repp, B. H. (2006). Rate limits of sensorimotor synchronization. Advances in Cognitive Psychology, 2(2), 163-181. https://doi.org/10.2478/v10053-008-0053-9
- Repp, B. H., London, J., & Keller, P. E. (2005). Production and synchronization of uneven rhythms at fast tempi. Music Perception, 23(1), 61–78. https://doi.org/10.1525/mp.2005.23.1.61
- Stone, R. (1985). In Search of Time in African Music. Music Theory Spectrum, 7, 139-148. https://doi.org/10.2307/745884
- Toussaint, G. T. (2003). Classification and phylogenetic analysis of African ternary rhythm timelines. In: Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science (pp. 25-36). Granada, Spain, July 23-27 2003.
- Toussaint, G. T. (2013). The geometry of musical rhythm: What makes a "good" rhythm good?. Boca Raton: CRC Press.
- Van Noorden, L., & Moelants, D. (1999). Resonance in the perception of musical tempo. Journal of New Music Research, 28(1), 43-66. https://doi.org/10.1076/jnmr.28.1.43.3122
- Waterman, R. (1952). African influence on the music of the Americas. In S. Tax (Ed.), Acculturation in the Americas (pp. 207-218). Chicago: University of Chicago Press.
APPENDIX: AUDIO AND VIDEO FOOTAGE OF EWE DRUMMING SURVEYED
- Burns, J. (Coll., Ed.) (2004, CD). Ewe drumming from Ghana. The soup which is sweet draws the chairs in closer. Topic Records.
- Burns, J. (Coll., Ed.) (2006, CD). Dzigbordi Haborbor, volume two. Community Empowerment Project.
- Burns, J. (Coll., Ed.) (2006, CD). Dzodze. Apeyeme Agbadza group, volume one. Community Empowerment Project.
- Burns, J. (Coll., Ed.) (2006, CD). Dzodze. Tornu Yeve Shrine ensemble. Music for ceremony. Community Empowerment Project.
- Burns, J. (Coll., Ed.) (2006, CD). Denu Dunyeno Haborbor, volume one. Community Empowerment Project.
- Burns, J. (Coll., Ed.) (2009, DVD included in monograph). Female voices from an Ewe dance drumming community in Ghana: Our music has become a divine spirit. Burlington, VT: Ashgate.
- Ghana Dance Ensemble/University of Ghana at Legon (2006, DVD). Dance-drumming of the Anlo-Ewe: An instruction. Vijay Rakhra Productions.
- Koetting, J. (Coll.) (2015). Ghana field recording collection. Archive available online (last accessed 2015/07) at https://repository.library.brown.edu/studio/collections/id_585/
- Ladzekpo, S. K. (Coll.) (1969, LP). Ewe music of Ghana. Folkways Records, AHM 4222.
- Locke, D. (Coll., Ed.) (1992, CD accompanying monograph). Kpegisu: A war drum of the Ewe. Tempe, AZ: White Cliffs Media.
- Locke, D. (Coll., Ed.) (1994, CD). Drum Gahu. good time dance music from the Ewe people of Ghana and Togo. Tempe, Ariz.: White Cliffs Media.
- Locke, D. (Coll., Ed.) (1998, CD included in monograph). Drum Gahu. An introduction to African rhythm. Tempe, Ariz.: White Cliffs Media.