Introduction
PROBABILISTIC analyses of music, using both Bayesian and information-theoretic approaches, have had much success in the prediction of key centres, and in the psychological modeling of pitch and harmonic expectation (reviewed by Huron, 2006; Pearce & Wiggins, 2012; Temperley, 2007). Most of this work has been done with Western tonal music, though some contributions have considered other modal styles, such as Indian music (Chordia et al., 2011). These studies use corpora of symbolic representations of the music under study to train the modeling algorithms. Our purpose here was to extend such models to non-tonal Western music. Since as far as we are aware no symbolically-encoded corpora of non-tonal music are available, we constructed one by an algorithmic procedure that uses classic principles of serialist composition. Our research question is whether such an algorithmically generated corpus proves useful in probabilistic modelling of pitch prediction. We address this question by training models on algorithmically generated corpora and using them to predict the pitches in canonical non-tonal works by Webern and Schoenberg and non-tonal keyboard improvisations.
Tonal and atonal music are primarily distinguished by whether or not particular pitches assume central prominence within the structure of a pitch hierarchy. Consistent with music compositional theory, pitch hierarchies are perceptible in both tonal and atonal music, as reflected for example in the degree to which a pitch is perceived to 'fit' with what has preceded it. Single pitch centres are prominent in tonal music, but not in atonal works, even though a pitch hierarchy still exists there (Dibben, 1994; Krumhansl, 1990). Serial composition, pioneered by Schoenberg and associates (c. 1908-1950), produces atonal music by a rigorous formalized organization of pitches. There is a 'prime' ordered series of pitches using all 12-pitch classes of the chromatic octave without repetition (the 'tone row', an originating source melody or motive), and commonly compositions are built from a single row. The row may be inverted, and both prime and inverse may be used forward and in reverse (retrograde) to form P, I, RP, and RI respectively. Each row transform may also be transposed as a whole, and the order in which the notes of the row or transform appear is sequential and conserved: local note group repetitions are not used in our application of this process (see Brindle, 1966; Forte, 1973; 1978) for discussion of the development and practical use of serial composition).
Here we deal mainly with 'monodic' (single strand) melodic materials, but polyphonic compositions (where multiple pitches can sound simultaneously) may be constructed by applying the serial processes vertically (across a set of different strands) and/or horizontally, with a separate serial process for each strand (although many other techniques exist). The frequency pattern of different pitch classes in serial music is consequently more homogeneous than in tonal music (e.g. Huron, 2006). As Huron noted, Schoenberg sought to be 'contra-tonal' in most of his serial compositions, and it has also been found that Schoenberg and other serialist composers had a statistical preference for symmetrical tone rows (Hunter & von Hippel, 2003).
Subsequent to the establishment of serialism, there was a move towards more flexible use of pitch and tonality, so that transparent tonality, multiple coexistent tonalities (polytonality) and 'post-tonal' (c.f. (Chew, 2005) styles followed. Terminology is awkward: 'post-tonal' has a chronological implication; and other terms have been used in contradictory ways. So we here refer broadly to non-tonal music, implying both a pure extreme with no tonal centres (as in some sections of serial compositions), and the common situation in which tonal centres appear intermittently but there is little long-term tonal organization. Thus there is a continuum from strongly tonal music to strongly atonal music, allowing for intermediate points in between. Even rigorous serialism rarely avoids the possible transient implication of tonal centres, and Berg in particular actively exploited this. Perception of atonal music forms a natural extension to that of tonal music: for example, the perceived segmentation and affective impact of parts of two (tonal) piano sonatas by Beethoven were not obliterated by conversion of their pitch structure into atonal sequences (Lalitte et al., 2009).
Approach
In order to be able to develop information theoretic models for non-tonal music, we first algorithmically composed a corpus of non-tonal monodic melodic pitch structures derived from serial compositional procedures, to test whether it can aid such predictive information-theoretic modeling. Existing information-theoretic models of music have focused on monodic single-stranded melodic music (e.g., Conklin & Witten, 1995; Pearce, 2005), due to the significant representational challenges caused by streaming (Bregman, 1990) in polyphonic music. Besides the monodic non-tonal corpus, we also constructed a corresponding diatonic (tonal) monodic corpus of major tonality melodic pitch structures based on closely similar serial compositional principles, as a point of comparison. If the serial organization principles are themselves important predictors of pitch sequencing, then even the resulting tonal melody corpus might have predictive power, particularly for non-tonal music. We assess the utility of the corpora in predicting the pitch structure of non-tonal music by Webern and Schoenberg, and non-tonal keyboard improvisations.
In what follows, we focus initially on the monodic corpora. Then to extend the approach to polyphonic music, we apply the algorithmic Serial Collaborator (Dean, 2014), which generates multi-strand piano music again using serial principles, and is used in performance (recordings are available with the cited paper, and elsewhere). Such algorithmic polyphonic music was created both from non-tonal and tonal melodic streams, using rigorous serial techniques, and the resulting polyphonic corpora were also used to model the non-tonal music under consideration. Throughout we will refer to melodic corpus and polyphonic corpus to distinguish the monodic single- and polyphonic multi-strand corpora (and in each case we have both a 'non-tonal' and a 'tonal' set).
We assess the utility of the algorithmically-generated corpora by training a probabilistic model of auditory expectation (Pearce, 2005) on them and then assessing the extent to which the trained model is capable of predicting pitch structure in various sets of music. We propose three hypotheses concerning the factors determining predictive success.
- Training on the serial non-tonal corpora will enhance modeling of non-tonal music, particularly serial non-tonal music. But we entertain the idea that non-tonal music, even if not composed by serial methods, is likely to be influenced by pitch patterns learnt from serial music, as discussed for example by Forte in relation to the compositions of Messiaen (Forte, 2002).
- Non-tonal music will be better modeled after training on the non-tonal corpus than after training on the tonal corpus.
- The (monodic) melodic corpora will be stronger predictors of monodic than of polyphonic music; and correspondingly, better than the polyphonic corpora as predictors.
Note that polyphony, that is, multiple strands of melody and/or chordal elements, normally reduces the clarity of the original pitch series. For example, when a chordal harmonic approach is superimposed on a serial melodic approach, the sequential features of the serial method are diminished because each individual chord no longer displays the original ordering of the constituent notes (it displays no ordering). Note also that a harmonic chordal structure could itself be composed in a rigorous serial manner, separately from any melodic material; this could then be the basis of a different alphabet of chord vectors (each alphabet member comprising several pitches), potentially used for composition and/or modeling. We have not yet pursued these possibilities.
To test our three hypotheses we trained models on the algorithmic corpora introduced above (tonal melodic, non-tonal melodic, tonal polyphonic and non-tonal polyphonic). We compare these models with two control conditions: first, models trained instead with two corpora of melodies with randomly selected pitches (see Methods section); and second, models trained instead on a comparably large tonal folk song corpus (Essen 'allerkbd' dataset, see below). We now summarize the features of these corpora which are relevant to their predictive capacity in terms of our hypotheses a, b and c: whether the feature is present, and whether it is expected to enhance or diminish predictive capacity for modeling monodic non-tonal music. Figure 1 shows examples of the opening 48 pitches of compositions within some of these corpora. Note that the effects of some of these features will depend not only on the qualitative aspects of the corpora, but also the quantitative, and hence our suggestions are offered with caution.
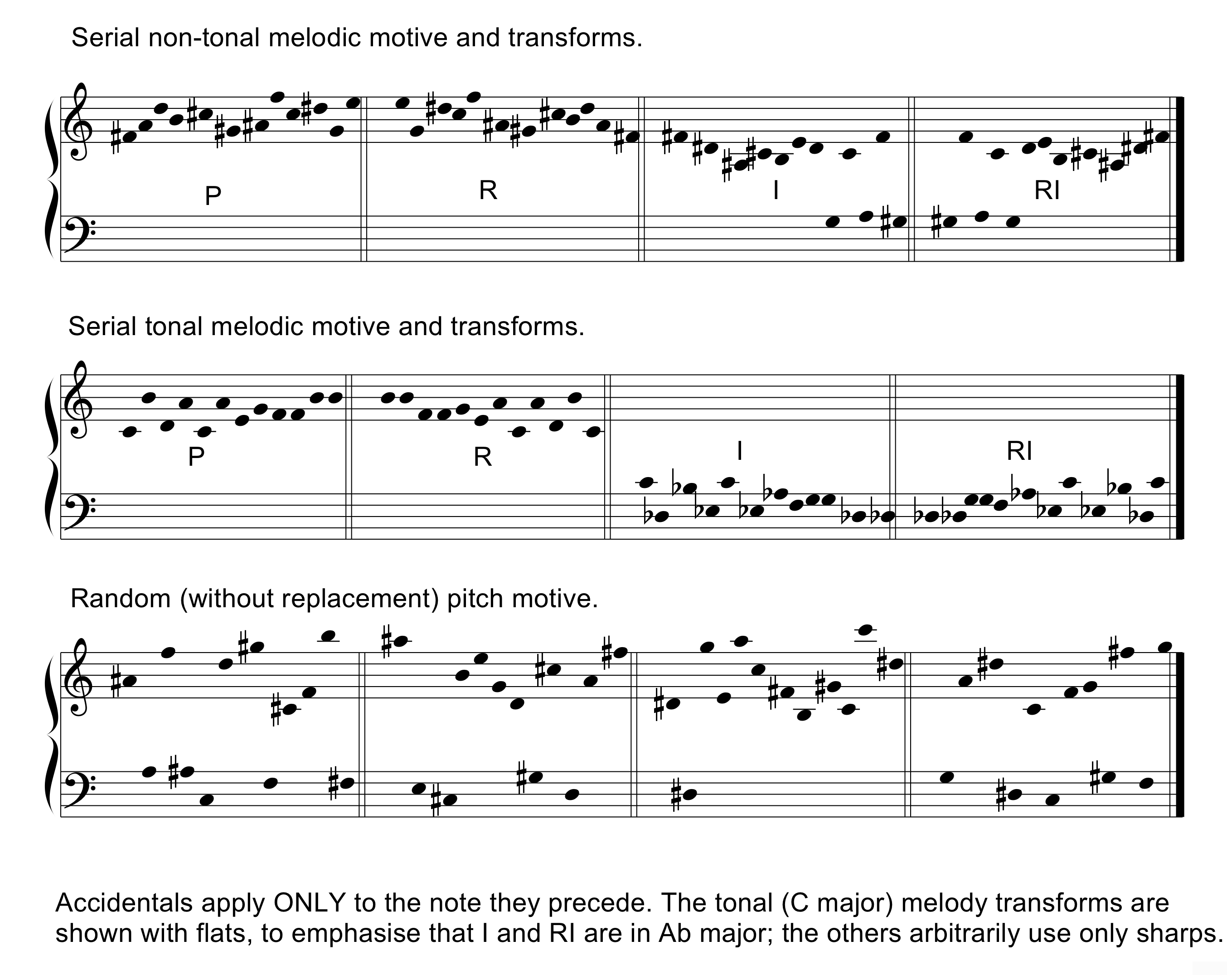
Figure 1. Examples of the algorithmic melodies and transforms. These are the sources for the algorithmic generation of the corpora (as detailed in Figure 2, and the text). It can be seen readily that pitches in the 'Serial' notations recur after events 12 and 24, and in the 'Random (without replacement)' notation recur after event 37.
- Corpus 1: Random melodic sequences. These are expected to have high information content, being unpredictable. Prediction enhancing features (for monodic non-tonal music): b (it is mainly non-tonal), c (it is single strand); diminishing features: a (it is not serial).
- Corpus 2: A serial melodic non-tonal corpus. Enhancing: a, b, c.
- Corpus 3: A serial melodic tonal corpus, with melodic passing notes (see Methods), to permit pitch diversity of the order of Western classical music. This serial tonal melodic corpus thus reflects serial procedures, but less rigorously, because 'passing' notes are allowed. It is entirely in major keys, but the passing notes may be extrinsic to the key in force at any moment. Enhancing: a, c; diminishing: b (the corpus is tonal).
- Corpus 4: A serial polyphonic non-tonal corpus in the form of two handed keyboard music (derived from 2). Note that while this corpus is played chordally, it is not constructed of systematic harmonic progressions: rather these are consequent on the melodic progressions, as discussed above. Enhancing: a, b; diminishing: c.
- Corpus 5: A serial polyphonic corpus in the form of two handed keyboard music. Derived from 3. Note that while this corpus is played chordally, it is again not constructed of systematic harmonic progressions: rather these are consequent on the melodic progressions. Consequently, the perceptible tonal features of corpus 3 are sometimes much further diminished. Enhancing: a; diminishing: b, c.
- Corpus 6: We also compared corpora 1-5, when appropriate, with a separate tonal melodic Folk song corpus (6), Essen (see Methods for details). Enhancing: c; diminishing: a, b.
To test our hypotheses, we apply models trained on these corpora to the task of predicting sequential pitch structure in four sets of non-tonal music.
- Music 1: Webern Piano Variations. A rigorous serial non-tonal composition, for two handed keyboard player, i.e. conceived polyphonically, harmonically and melodically. Hypothesized features of a corpus which should enhance the modeling this piece: a, b; diminishing feature: c.
- Music 2: Schoenberg Pierrot Lunaire Movement 7. A non-tonal composition for two melodic voices, not constructed with rigorous serial procedures, but showing elements of inversion and retrogradation. Few notes coincide in the two voices: they are probably not conceived harmonically in the ways that chordal piano passages are. Hypothesized enhancing features: b, c; diminishing feature: a.
- Music 3: Non-tonal sections of performances by professional piano improvisers. These polyphonic performances are conceived both melodically and harmonically, and the non-tonal sections can be discerned by pitch class interval frequencies. They are not rigorously serial, and rather than precise retrogrades contain contour relationships in the melodic elements. Enhancing feature: b; diminishing features: a, c.
- Music 4: Tonal sections of performances by professional piano improvisers. As for the non-tonal sections, these polyphonic performances are conceived both melodically and harmonically, and can be discerned by pitch class interval frequencies. They are not rigorously serial, and rather than precise transpositions, for example, contain contour relationships in the melodic elements. Diminishing features: a, b, c.
Our approach is slightly different from standard corpus analysis methodology, which involves analyzing a corpus to identify significant musical structures within it. Here we use a probabilistic model to examine relationships between corpora by training the model on one (Corpus 1–6) and using it to predict another (Music 1–4). The extent to which the trained model successfully predicts the music reflects the degree to which the training corpus contains structure that is similar to, and hence predictive of, the music to which the model is applied. In addition, most of the corpora (all except Essen) that we use to train our models are algorithmically generated, which has the advantage that we can isolate the kinds of structure introduced (e.g. strictly serial vs tonal) to see if particular structures are predictive of the music, as indicated in our distinctions between factors a-c above. Our goal here is to examine whether these algorithmically-generated corpora, constructed according to serial principles, are predictive of non-tonal music and, if so, which principles of construction are most predictive.
Methods
Algorithmic Construction of Non-tonal and Tonal Melodic (Monodic) Corpora
The first author coded patches in Max/MSP (v5, Cycling74) to algorithmically manipulate pitch sequences and record the melodic output. Rhythmic structure was not varied in these sequences (merely the isochronous sequence of notes) nor did it form part of our analyses.
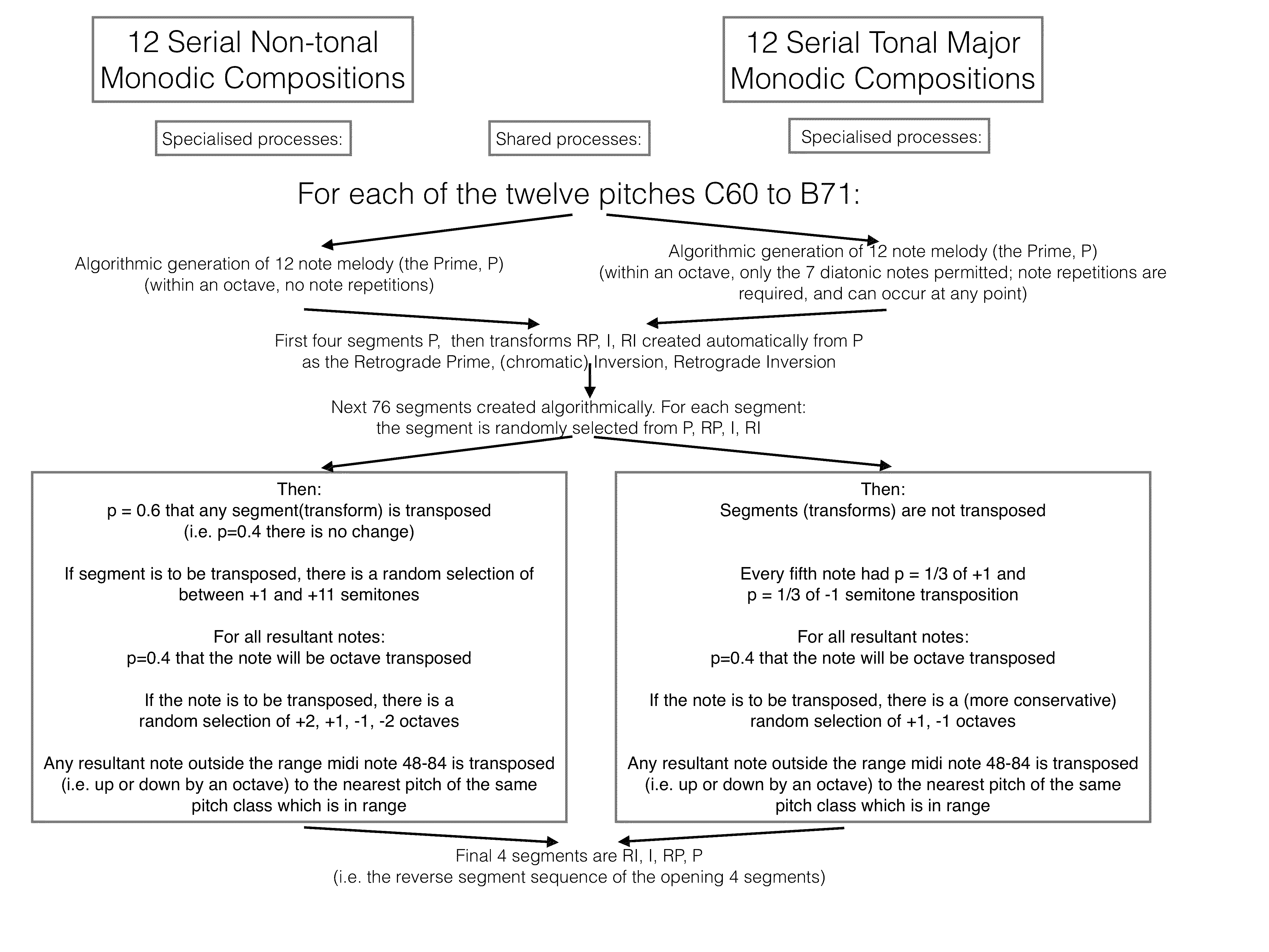
Figure 2 summarizes the overall procedure that was followed to create the experimental corpora. To form Corpus 2, the serial non-tonal melodic compositions, in keeping with Schoenbergian tradition we constructed tone rows, each comprising a sequence of notes including one occurrence of each of the 12-pitch classes of the Western equal-tempered chromatic octave. We created 12 tone rows (P), one commencing with each of the 12 pitches between middle C (midi note 60) and midi note 71, by a constrained stochastic process (there are c.9.8 million unique tone rows, as some of the 12 factorial random rows are identical by transposition, see Hunter & von Hippel, 2003). We then generated 1008 sequential note events from each row following fully defined serial rules as follows, and without permitting local pitch repetitions. Each 1008-note piece had the same sequence of 84 12-note sections. First, there were four sections P, RP, I, RI (untransposed). Each of the next 76 sections was a random selection from the 4 row transforms, and two compositional variabilities were rigorously superimposed on each of these sections: first, there was a 60% chance of a random upwards transposition of that transform by +1 to +11 semitones (this changes the pitch class of each note of the section); second, there was a 40% chance of any individual note being transposed 1 or 2 octaves up or down (this does not change the pitch class of the note). Note that none of these transpositions change the intervals between successive pitch classes (bearing in mind that because of the transpositions in the central 76 sections, the row can occur with any pitch class contributing its first note in a given rendering). In the final 4 sections, the untransposed RI, I, RP and P were played (reverse order to the outset). Overall pitch was constrained within the range 48-84.
To form the novel serial but tonal Corpus 3, major melodies were first constructed, in a closely similar fashion. We made one melody of twelve notes in each of 12 major keys, using the 7 diatonic major pitches, and with pitch repetition allowed before complete usage of the set of pitches (i.e. some of the twelve-note melodies did not use all seven pitches, and they all contained note repetitions, unlike the serial non-tonal melodies). Chromatic inversion of a major melody (but not a minor) creates a transform which is now in the major key four semitones lower than that of the original melody, and hence we were again able to use transforms P, RP, I, and RI while moving between two major keys. For example, the C major scale ascending, when chromatically inverted gives rise to a descending A♭ scale, again starting on C, four semitones above the tonic A♭.
The use of retrograde and inversion in tonal music was well understood by 15th century composers such as Obrecht (Todd, 1978) but does not seem to have been a common technique since. We used it here so as to bring compositional similarities to the atonal and tonal corpora. Tonal sequences of 1008 notes were constructed similarly to the non-tonal corpus. The first four and last four sections were melody transforms in the same order as for the non-tonal corpus. In the intervening 76 sections compositional variabilities were again introduced: every fifth note had a ⅓ chance of being transposed down 1 semitone and a ⅓ chance of being transposed up 1 semitone (this changes the pitch class of the transposed note). Every note in these sections might also be transposed up or down one octave (40% chance of change: this does not change pitch class). The chromatic transpositions were intended to mimic melodic decorations, and the more conservative octave transposition (by no more than one octave) is appropriate for tonal music. There were no transpositions of a transform as a whole (unlike the method used for the non-tonal melodies). Again unlike the transpositions used in the non-tonal melody generation, this overall process can create pitch class successions in the tonal melodies that do not conserve the original pitch intervals, but which generally conserve the pitch contour, and do not destroy the current tonality. These features were necessary both for compositional diversity, and to ensure that all the 12 pitch classes were used. Overall pitch was again constrained between 48-84. For both Corpora 2 and 3, the algorithms normally generate more pitches above than below middle C, as in common practice keyboard music.
We also constructed two control corpora. Corpus 1a was a set of 12 compositions with pitches between 48 and 84 chosen at random without replacement until all had been used (so after all 37 pitches had been chosen all became available for the next of 27 rounds of random choice). Corpus 1b comprised 12 compositions with pitches chosen at random with replacement; thus unlike 1a, this corpus contained some immediate or closely adjacent repetitions of pitches, and had a less uniform distribution across pitches. These two random corpora each consisted of 27 x 37 (999) events, to be similar in size to the non-tonal and tonal melodic corpora.
Construction of Polyphonic Corpora: The Algorithmic Serial Collaborator
Because most music (particularly non-tonal music) is polyphonic (i.e. combines more than one melody strand together with simultaneously articulated multi-note chords), the first author also constructed a MAX patch which generates 'two-handed' keyboard performances. This algorithm has been described in detail elsewhere (Dean, 2014), and is in regular use for creative work in improvisation and composition. The patch takes a melodic sequence (such as those of the non-tonal and tonal melodic corpora described above), to generate music which is normally sounded on a Midi-driven piano, such as the PianoTeq physical synthesis grand piano models. It is used in a very simple manner here.
Two-handed (polyphonic) compositions were generated from each of the non-tonal and tonal melodic (monodic) sequences comprising the respective melodic corpora, to form Corpora 4 and 5 respectively, as follows. The pitches were used in exactly the sequence in which they occurred in the corpora, but with one 'hand' realizing the first 50% of the notes sequentially, and at the same time the other hand realizing the latter 50%. Each hand can play single notes or chords of up to 4 notes, with the maximum chord size taken from the Webern Piano Variations analysed below. The melodic (monodic) corpora all use the pitch range 48-84; for the polyphonic corpora the 'left hand' is transposed to the range 24-60 and the 'right hand' to 60-96, thus the pitch range of the corpora is enlarged. The Serial Collaborator's chords remove the original sequencing of the constituent notes, as they are now sounded simultaneously. There is also re-sequencing as a consequence of the coexistence of the two hands, so that for example, if both hands start together, then notes 1-20 and c. 505-524 will be likely to mingle sequentially in the case of a Serial Collaborator composition based on the 1008 note melodies. This feature of serial composition is constitutive, and contributes to the flexibility of the method. Given this intermingling, it now becomes possible for the same note class (but not pitch, other than C 60) to be occasionally enunciated twice in immediate sequence (or simultaneously in a chord) because of the polyphony. Note that in general the non-tonality of the non-tonal melodies is conserved in making these polyphonic compositions, but the tonality of the tonal melodies is potentially perturbed towards non-tonality, because sections corresponding to distinct tonalities may be sounded together. These two-handed keyboard works are arguably more ecologically realistic than the melodic sequences, and this aspect was enhanced by providing rhythmic and dynamic (key velocity) pattern generation for the patch, which changes the intermingling of the sequences. These patterns may be generated independently of the pitch patterns. Since pitch structure is the focus of the present work, only the resulting (re-sequenced) stream of single pitches was analysed. The streams are recorded as text or Midi-files containing the pitch sequences as if they were again monophonic, with chords arpeggiated from low pitch to high (as also described next for the Webern piano music).
Encoding the Pitch Structure of Non-tonal Compositions as Modeling Subjects
Schoenberg's Pierrot Lunaire, Movement 7, a non-tonal (but not serial) composition for flute and voice was encoded for modeling. The two parts were separated (238 events in total), and the pitch sequences of each were listed manually. Similarly, the complete pitch sequence of Piano Variations Op. 27 of Webern, a canonical serial work, was encoded. Where chords occur, their constituent pitches were entered successively from low to high, thus producing some re-sequencing of the pitch series as previously discussed.
Modeling the Corpora with IDyOM
The Information Dynamics of Music (IDyOM) model considers multiple viewpoint n-gram statistics of melodic (monophonic) sequences, like those of our corpora, and can predict several features of pitch sequences, phrase segmentation, and perceptual expectations (Pearce, 2005; Pearce & Wiggins, 2006; 2012) 2. Space does not permit a detailed re-exposition of IDyOM, but the references quoted provide substantive introductions. Traditional corpus analysis often proceeds by analyzing musical structure within a given corpus. In contrast, IDyOM is trained on a corpus, and then predicts another. The greater the sharing of structure between the corpora, the better the prediction. IDyOM generates a conditional probability distribution governing some property of the next event in the musical sequence – here, the pitch of the next note. We use the negative log probability – or Information Content (IC) – as a measure of unexpectedness, in context, for each note in a piece. Averaged over notes and compositions, we can use IC as a measure of prediction performance – models making accurate predictions by predicting notes with a high probability, will have a correspondingly low IC, and vice versa.
In generating probabilistic expectations, IDyOM considers the influence of both short-term statistical information learned dynamically from the current piece(s), the STM (short term model), and the long-term impact of prior exposures to music, the LTM (long term model). The LTM can be considered to model the musical experience of a listener in place before exposure to new material. IDyOM itself can be pre-trained on chosen corpora, modeling the impact of such experience as a component of its LTM. Different 'viewpoints' (Conklin & Witten, 1995) may be used to combine information from different representations of the music (at different levels of abstraction), taking into account pitch, rhythm, dynamics and their interrelations, but here we are only concerned with pitch information. The features directly related to this are chromatic pitch (note number: termed Pitch), chromatic interval between successive notes (PitchInterval) with sign preserved (i.e. descending -, ascending +), and the equivalent parameters expressed in terms of chromatic pitch class, with C (60) as fundamental (PitchClass and PitchClassInterval). PitchClass is Pitch modulo 12 while PitchClassInterval is PitchInterval modulo 12, but with sign again preserved. PitchInterval and PitchClassInterval are thus identical unless the interval is larger than 11 semitones. Here we take the best model of a piece or corpus to be that which returns the lowest mean IC. We compare STM and LTM models, their combination (BOTH), and models in which the LTM progressively learns the new material (LTM+). The model combining STM and LTM+ is termed 'BOTH+'. Since the alphabet size (the number of different pitches present in the model) influences the IC (because every pitch has to be assigned at least some probability), we are careful to pre-expose all models, the STM models included, to the alphabet of the complete training set (corpus) which is being studied; even though the STM is not pre-trained. The polyphonic corpora have a larger alphabet than the monodic. We routinely use ten-fold cross-validation, so that our IC values constitute reliable, generalizable estimates. This involves forming 10 disjoint subsets of a corpus, and training the model 10 times, each time omitting a different subset to use for testing; the 10 mean IC values so obtained are averaged. Note again that although we generated genuine polyphonic corpora (4-5), we analyze them as single linear sequences, as if monodic, and we do the same for the polyphonic pieces we model.
Results
We consider first whether the non-tonal and tonal melodic (monodic) corpora contain distinctive statistical features; second, whether the non-tonal and tonal polyphonic corpora contain distinctive statistical features and how these relate to the melodic corpora; and finally the predictive capacities of the algorithmically-generated corpora for non-tonal music, in comparison with the random and Essen corpora.
Basic Features of the Algorithmic Compositional Monodic Corpora 2 and 3
It was expected (as mentioned above) and observed in listening that for the non-tonal melodic corpora there might be occasional bursts of tonality; and for the tonal melodic corpora, there might be short apparent impacts of other keys, as well as of the key of the inversion. The pitch class distributions for the non-tonal melodic (monodic) transforms were as required by the algorithm: all 12 classes show identical frequency. Pitch class distributions were non-identical for the monodic tonal corpus, and for both corpora as expected there were more notes above than below C60 (see Figure 1).
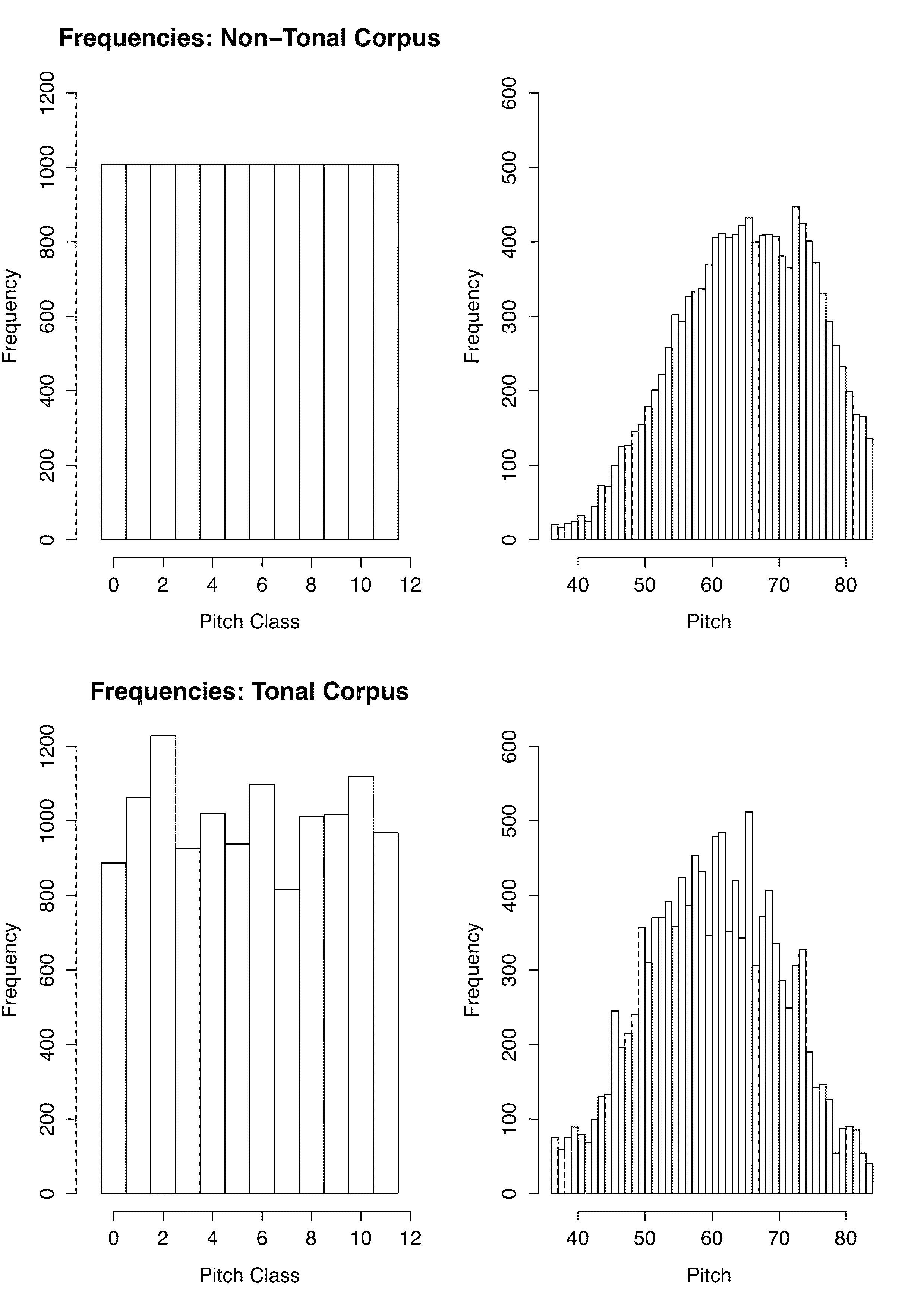
Figure 3. Pitch and Pitch-Class Frequencies in the Algorithmic Melodic Corpora. The top row is for the Non-Tonal and the bottom for the Tonal Corpus. The left column is for pitch class, and the right for pitch. Note that the tonal distributions reflect not only the prime (P), but also I, PI, PR, and the transpositions; thus they do not reveal the classical melodic tonal hierarchy.
Characterising the Algorithmic Melodic (Monodic) Corpora 2 and 3 by IDyOM Modeling
It was important to assess how models of our new algorithmic corpora compare with each other, and with those using existing corpora such as the Essen Folk Song collection (Schaffrath, 1995), so as to establish their potential as pre-training entities with possible distinct predictive capacity. Since the size of a corpus may influence its predictive capacity, the melodic non-tonal and tonal corpora (corpora 2 and 3) were split into two halves. In this way the impact of using pre-training on either one corpus or a mixture of two could be fairly tested. Table 1 shows the results of these analyses, using IDyOM. For each corpus and model configuration, a combination of individual viewpoints was optimized using hill-climbing with mean IC as the evaluation function (Pearce, 2005; Pearce & Wiggins, 2006). Consistent with previous results (Pearce, 2005), in all cases the BOTH+ model provided the lowest IC with or without pre-training for the non-tonal and tonal melodic corpora.
We also compared pre-training with existing tonal corpora. We selected a corpus of German folksongs (Essen collection allerkbd) from the Essen Folk Song Collection (Schaffrath, 1995) containing 5915 events (110 compositions) comparable in size with half of one of our algorithmic corpora.
| Viewpoints Selected | Model Configuration | Pre-training | Mean IC |
| Modeling the Non-tonal Melodic Dataset 1-6 | |||
| Pitch PitchInterval PitchClass PitchClassInterval | BOTH+ | None | 3.80 |
| As above | BOTH+ | Non-tonal pieces 7-12 | 3.80 |
| As above | BOTH+ | Tonal pieces 7-12 | 3.79 |
| As above | BOTH+ | Non-tonal 7-12 and tonal 7-12 | 3.79 |
| As above | BOTH+ | Essen | 3.90 |
| Modeling the Tonal Melodic Dataset 1-6 | |||
| Pitch PitchInterval PitchClass | BOTH+ | None | 4.05 |
| As above | BOTH+ | Non-tonal pieces 7-12 | 4.08 |
| As above | BOTH+ | Tonal pieces 7-12 | 4.07 |
| As above | BOTH+ | Non-tonal 7-12 and tonal 7-12 | 4.07 |
| As above | BOTH+ | Essen | 4.13 |
| Modeling the Melodic Random Corpus (generated with replacement) | |||
| Pitch PitchInterval PitchClass PitchClassInterval | LTM+ | None | 5.26 |
| Modeling the Melodic Random Corpus (generated without replacement) | |||
| As above | LTM+ | None | 5.25 |
| Modeling the Essen :allerkd German folk song tonal Corpus | |||
| Pitch PitchInterval | BOTH+ | None | 2.46 |
Note to Table 1. Even the small IC changes are statistically significant (p <0.01), when judged by a full comparison of the multiple IC values obtained for each pitch event in the corpora. This is normal with data of this kind (see Pearce, 2005). In this Table and later ones bold indicates the minimum IC values.
The models reveal distinctive features of the algorithmic melodic corpora as shown in Table 1. For the tonal melodic corpus, the following viewpoints were selected: Pitch, PitchInterval, PitchClass, yielding an overall IC, without pre-training, of 4.05. For the non-tonal melodic corpus, all four viewpoints were selected: Pitch, PitchInterval, PitchClass, PitchClassInterval (consistent with the presence of many intervals greater than 11 semitones), yielding an overall IC of 3.8. Although these values are much higher than those for our tonal corpus (Essen: 2.46), they are not at ceiling, as they are much lower than the IC values for the two random corpora 1a and b (5.25, 5.26) for which all four viewpoints were also selected. The algorithmic non-tonal and tonal melodic corpora therefore contain significantly more systematic internal statistical structure than the random corpora.
Preservation of PitchClass in the model of the tonal monodic corpus (as well as in that of the non-tonal) may reflect the fact that our manipulations of whole major key melodies, which were based entirely on untransposed P-RP-I-RI segments, generate only two clear-cut keys (C and A♭ major if the starting melody is in C major). It is interesting that PitchClassInterval was a predictor for the random corpora, presumably again a consequence of the presence of large intervals; though as expected these were poorly cohesive as judged by the high IC.
Pre-training with the non-tonal and tonal melodic monodic corpora slightly enhanced prediction performance of the model for the non-tonal corpus. But the effects of pre-training on models for all other corpora were either neutral or negative, suggesting both the statistical homogeneity of the corpora (further training from the other half of the corpus does not improve performance) but also their difference, in statistical terms, from other corpora 3. Overall, therefore, these slight effects of pre-training suggest that the algorithmic melodic sequences are internally very consistent, reflecting the uniform use of the P-RP-I-RI transformation approach. The non-tonal and tonal melodic corpora are substantially distinct from existing tonal music, as judged by the dramatically lower IC for the Essen set, and its incapacity to enhance any of these models.
Characterising the Polyphonic Corpora 4 and 5 by IDyOM Modeling
Table 2 shows selected analyses of the 'two-handed' polyphonic serial corpora (treated after linearising to a monodic sequence, as described in Methods). We again used hill-climbing to determine the optimum set of features, and used these for comparisons of the impact of pre-training with different corpora. Consistent with the re-sequencing involved in the keyboard performances (discussed above) the information contents of these corpora were substantially increased over those of the algorithmic melodic (monodic) corpora from which they were derived. Those for the non-tonal corpus were in this case higher than for the tonal. The best models for the two sets, non-tonal and tonal, were similar in form to those for the melodic corpora. However, for the non-tonal set, pitch class was no longer a useful predictor, though pitch class interval remained (alongside pitch and pitch interval). This likely reflects the increasing mixing of the melodic strands and thus of P, I, RI, RP components in the construction of the polyphonic corpora. For the tonal polyphonic corpus the optimal model form was unchanged from that for the tonal melodic monodic corpus: pitch class but not pitch class interval was predictive, together with pitch and pitch interval.
For both tonal and non-tonal polyphonic corpora, pre-training on a withheld portion of the corpus, or on a portion of the other polyphonic corpus, or both, improved prediction performance, with the greatest improvement resulting from the combined tonal and non-tonal polyphonic corpora in both cases. The Essen corpus also modestly improved performance for the tonal polyphonic but hardly for the non-tonal corpus. The positive impact of pre-training with a withheld portion probably reflects the greater inhomogeneity of the polyphonic corpora compared with the monodic corpora.
| Viewpoints Selected | Model configuration | Pre-training | Mean IC |
| Modeling the Non-tonal Polyphonic Dataset 1-6 | |||
| Pitch PitchInterval PitchClassInterval | BOTH+ | None | 5.43 |
| As above | BOTH+ | Non-tonal Polyphonic pieces 7-12 | 5.40 |
| As above | BOTH+ | Tonal Polyphonic pieces 7-12 | 5.40 |
| As above | BOTH+ | Non-tonal 7-12 and tonal 7-12 | 5.38 |
| As above | BOTH+ | Essen | 5.42 |
| Modeling the Tonal Polyphonic Dataset 1-6 | |||
| Pitch PitchInterval PitchClass | BOTH+ | None | 5.36 |
| As above | BOTH+ | Tonal Polyphonic pieces 7-12 | 5.35 |
| As above | BOTH+ | Non-tonal Polyphonic pieces 7-12 | 5.29 |
| As above | BOTH+ | Non-tonal 7-12 and tonal 7-12 | 5.26 |
| As above | BOTH+ | Essen | 5.33 |
Given that the characteristics of our four main algorithmic corpora (2-5) were appropriate for our purpose, we next proceed to the core question of whether the non-tonal melodic (monodic) corpus improves IDyOM prediction performance for composed or improvised non-tonal music. As explained in the introduction, we can predict that performance will be enhanced most for Music 1 (Webern), being serial and non-tonal, and to a lesser extent for Music 2 (Schoenberg), being non-serial though non-tonal. Music 3 (non-tonal improvisation) and 4 (tonal) are ecologically valid keyboard improvisations, and so expected to be less rigid in their pitch patterns: nevertheless we expected the non-tonal algorithmic corpora to enhance prediction performance of our models for at least the non-tonal segments (Music 3).
Using the Algorithmic Corpora for Modeling Non-tonal Compositions by Webern and Schoenberg
There are several ways to address the question of whether a given musical corpus has predictive capacity for particular works; in other words, whether it contains structure which is also important in the works being modeled. Perhaps the most straightforward is to ask whether the prediction performance of a short-term model (representing a totally naïve listener) is improved when it is supplemented with background knowledge of the corpus (the LTM) in a BOTH+ model. Here we hypothesized that background knowledge of the melodic non-tonal corpus would be most effective, of the melodic tonal corpus ineffective, and of the Essen corpus ineffective.
Consistent with this hypothesis, the algorithmic melodic non-tonal corpus improved prediction performance for the (linearized) serial Webern Piano Variations as a whole, while the tonal corpus and Essen had a negative impact on performance, as shown in Table 3. Here we make comparisons with the STM, which produced an IC of 4.27. The non-tonal corpus improved prediction performance in a viewpoint-optimized BOTH+ model (IC 4.21), by using the PitchClassInterval viewpoint. Adding the tonal melodic corpus to this model impaired prediction performance (4.37). Essen was ineffective. Qualitatively similar results were found when the polyphonic corpora were used for pre-training, where the non-tonal but not the tonal corpora showed some predictive capacity, although as expected the effects were much smaller here (viewpoint-optimized BOTH+, IC: 4.26).
| Viewpoints selected | Model configuration | Pre-training | Mean IC |
| Modeling with the melodic corpora | |||
| Pitch PitchInterval | STM | None | 4.27 |
| PitchClassInterval | BOTH+ | Essen | 4.59 |
| Pitch PitchInterval | BOTH+ | Melodic non-tonal Corpus 1-12 | 4.37 |
| Pitch PitchInterval PitchClassInterval | BOTH+ | Essen | 4.73 |
| Pitch PitchInterval PitchClassInterval | BOTH+ | Melodic non-tonal Corpus 1-12 | 4.21 |
| Pitch PitchInterval PitchClassInterval (Optimised with the Non-Tonal Melodic Corpus) | BOTH+ | Melodic non-tonal Corpus 1-12 and Melodic tonal Corpus 1-12 | 4.37 |
| Modeling with the polyphonic corpora | |||
| Pitch PitchInterval | STM | None | 4.27 |
| Pitch PitchInterval | BOTH+ | Polyphonic non-tonal Corpus 1-12 | 4.26 |
| Pitch PitchInterval | BOTH+ | Polyphonic Non-Tonal Corpus 1-12 and polyphonic tonal Corpus 1-12 | 4.27 |
Table 4 shows results for Schoenberg's Pierrot Lunaire, Movement 7, arguably a contra-tonal (though not serial) composition for flute and voice, for which we considered each voice separately (238 events in total). We hypothesized only limited predictive capacity for our non-tonal melodic corpus (and none for the tonal melodic corpus), because the composition itself is not serial but is non-tonal. Given that the composition is not chordal, we also expected no or very slight predictive benefit in pre-training on our polyphonic corpora. In agreement, the optimized STM produced an average IC of 4.48 while improved prediction performance was again achieved with viewpoint optimized BOTH+ models pre-trained on the melodic non-tonal corpus (4.41) and this effect was reduced when the tonal corpus was added (4.43). Essen was again ineffective. Here, pre-training on the non-tonal polyphonic corpora did not yield any performance improvements.
| Viewpoints selected | Model configuration | Pre-training | Mean IC |
| Modeling with the melodic corpora | |||
| Pitch PitchInterval PitchClassInterval PitchClass | STM | None | 4.49 |
| Pitch PitchInterval | BOTH+ | Essen | 4.77 |
| As above | BOTH+ | Melodic non-tonal corpus 1-12 | 4.41 |
| As above | BOTH+ | Melodic non-tonal corpus 1-12 and Melodic tonal corpus 1-12 | 4.43 |
| Modeling with the polyphonic corpora | |||
| Pitch PitchInterval PitchClassInterval PitchClass | STM | 4.52 | |
| Pitch PitchInterval | BOTH+ | Polyphonic non-nonal corpus 1-12 | 4.76 |
| As above | BOTH+ | Polyphonic Non-Tonal corpus 1-12 and Polyphonic tonal Corpus 1-12 | 5.31 |
Overall, the results for modeling these non-tonal compositions were consistent with our hypothesis that the algorithmic non-tonal monodic corpus would embody melodic information predictive of actual non-tonal music.
Using the Algorithmic Corpora for Modeling Tonal and Atonal improvisation.
As an ecologically valid assessment of improvised music, we examined performances by three professional piano improvisers from an earlier study (Dean et al., 2014) who were requested to perform c.3 minutes of improvisation in an ABA form, A 'tonal', B 'atonal' and A again tonal. No discussion of the meaning of these terms was given, and there were no queries from the performers (neither author performed). A Yamaha Disklavier Grand Piano was used, and midi recordings made of the pitch sequences performed. As discussed above, chordal notes appear in the resultant linearized pitch series in the sequence they entered the MIDI-stream.
We determined whether the algorithmic corpora aided in modeling the less ('atonal') and more tonal sections. We expected liberal interpretations of 'tonal' and 'atonal', but a meaningful contrast. The contrast was confirmed by computational segmentation of the performances (see Figure 4), as we detailed previously. There were 634 events in the three 'atonal' segments, and 772 events in the six 'tonal'. Tables 5 and 6 summarize the modeling undertaken.
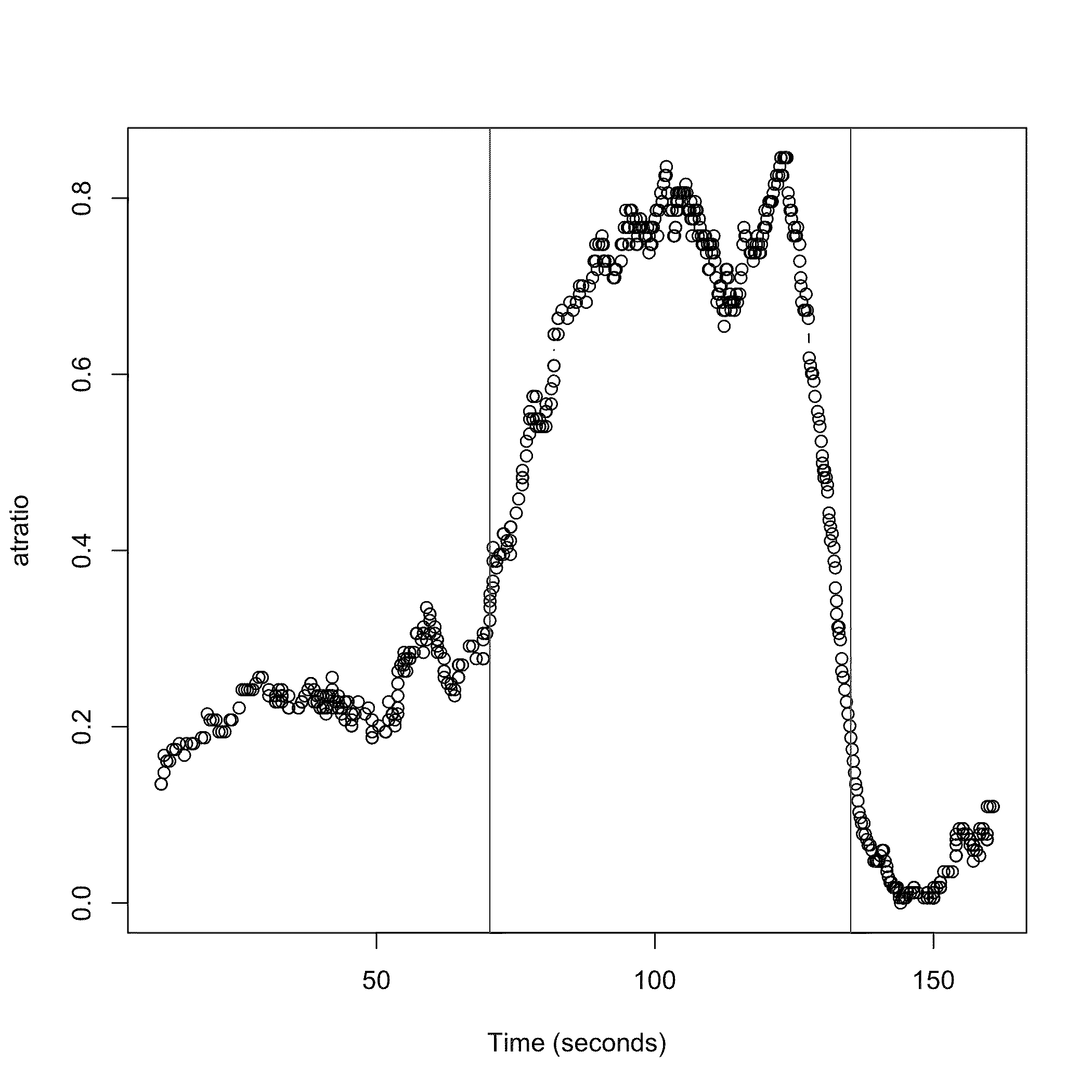
Figure 4. Segmentation of a piano improvisation focused on tonal-atonal transitions. A simple measure of "tonalness" is shown as "atratio" (atonal:tonal ratio) with respect to time across the performance. We measured with moving windows of 80 successive events the ratio of the number of 1, 6 and 11 semitone intervals (more dissonant, less tonal) to the number of occurrences of the other (more tonal) intervals between pairs of notes. This ratio was measured for each note in relation to each of the following six notes, and averaged for the 6 note-pairs. This range was chosen because it was the lowest integer value which exceeded the average number of notes played in a chord. Nevertheless, the notes were treated in the sequence they occurred in the MIDI-file, so that notes which are heard as chords are separated. Values so obtained were then averaged across the window of 80 events, and then the window moved forward by one event. Thus there were 79 less time points in the resultant atratio series than there were in the original data. The time series of these values was segmented in a principled manner using the R library ChangePoint (by Rebecca Killick). The central portion is taken to be the 'atonal' segment, fulfilling the requested referent for improvisation. Similar but less discriminating segmentation was achieved by using windowed pitch class entropy (not shown; a suggestion from David Temperley).
| Viewpoints Selected | Model configuration | Pre-training | Mean IC |
| Atonal Segments | |||
| Pitch PitchInterval | STM | None | 5.35 |
| As above | BOTH+ | Essen (tonal) | 6.04 |
| As above | BOTH+ | 12 non-tonal pieces | 5.32 |
| As above | BOTH+ | 12 tonal pieces | 5.30 |
| As above | BOTH+ | 12 non-tonal plus 12 tonal | 5.27 |
| Tonal segments | |||
| Pitch PitchInterval PitchClass | STM | None | 4.95 |
| As above | BOTH+ | Essen (tonal) | 5.38 |
| As above | BOTH+ | 12 non-tonal pieces | 4.99 |
| As above | BOTH+ | 12 tonal pieces | 4.98 |
| As above | BOTH+ | 12 non-tonal and 12 tonal | 4.96 |
The 'atonal' performed segments have higher information content than the tonal, comparable in magnitude with those shown above for the algorithmic polyphonic corpora, whereas the relationship is reversed for the algorithmic non-tonal vs tonal algorithmic melodic monodic corpora, as shown in Table 1. This is likely due to an increased simplicity of the improvised tonal sections relative to the algorithmic tonal melodic corpora. It may also reflect the lesser precision (higher unexpectedness) with which a performer implements the concept of 'atonality' in comparison with the rigor of the serial algorithm. Consistent with this, the best analysis for distinguishing the tonal and atonal segments of the performances was simple in comparison with the serial procedures (see legend to Figure. 4).
Our hypothesis was that the non-tonal melodic (monodic) corpus, at least, would be predictive for the less tonal improvised segments, and the tonal corpus less so. We hypothesized that the tonal corpus would also be predictive for the tonal improvisation segments, but Essen would only have predictive capacity for the tonal segments. Table 5 shows the results of the analysis for models pre-trained on the melodic corpora to test this.
In the case of the non-tonal improvisation segments, the hypothesis was supported for the non-tonal melodic corpus and for Essen, and there was also benefit from knowledge of the tonal melodic corpus. Prediction performance is improved by supplementing the STM (IC: 5.35) with an LTM+ trained on the melodic tonal corpus (BOTH+: 5.30), one trained on the melodic atonal corpus (BOTH+ 5.32) and one trained on both melodic corpora (BOTH+: 5.27). For the tonal improvisation segments, prediction performance is not improved by supplementing the STM (IC: 4.95) with LTM+ models trained on any combination of the melodic tonal or non-tonal corpora: this aspect of the hypotheses was not supported. The viewpoints selected for predicting the atonal segments were Pitch and PitchInterval, while for the tonal segments, these viewpoints were supplemented by PitchClass in the optimal model, consistent with a strong tonal feature in the performances. Prediction performance was not improved by training models on the polyphonic corpus in any of our cases (see Table 6).
| Viewpoints selected | Model configuration | Pre-training | Mean IC |
| Atonal segments | |||
| Pitch PitchClassInterval | STM | None | 5.67 |
| As above | BOTH+ | Non-tonal polyphonic pieces 1-12 | 5.77 |
| As above | BOTH+ | Non-tonal and tonal polyphonic pieces 1-12 | 6.51 |
| Tonal segments | |||
| Pitch PitchInterval PitchClassInterval | STM | None | 5.12 |
| As above | BOTH+ | Tonal polyphonic pieces 1-12 | 5.55 |
| As above | BOTH+ | Non-Tonal and Tonal polyphonic pieces 1-12 | 6.04 |
Note to Table 6: Note that the substantially higher IC values for the STM models in this Table in comparison with Table 5 are an example of the impact of the increased alphabet size in the polyphonic corpora.
In summary, the algorithmic melodic (monodic) corpora were predictive for non-tonal improvisations (Table 5), and even the tonal melodic corpus had a positive impact. Taken with the introduction in this case of PitchClass as a predictor, this suggests that the maintenance of interval repetition based on the serial method and referenced to the ongoing tonality of the improvisation might be influential. The algorithmic polyphonic corpora were not effective on the tonal and atonal segments (Table 6). This further supports the idea that improvisers use distinctive methods for achieving referent targets, and experience and introspection (by the first author) suggests that the two hands may be used in a more autonomous way than would be implied by splitting continuous serially-derived note streams into melodic and chordal notes. Thus it might be predicted that the polyphonic corpora would have more power in models of the Webern piano piece for which they were intended; and this was indeed observed above, even though the effect was slight.
Discussion
Our main conclusion is that the algorithmic serial melodic (monodic) compositions are useful in information-theoretic modeling of pitch sequences in a range of non-tonal music, both composed and improvised. Indeed, even the algorithmic serial tonal melodic corpus provided some predictive power, though much less so than the non-tonal melodies, as hypothesized. Specifically, the resultant corpora were predictive in modeling the atonal segments of piano improvisations and non-tonal compositions by Webern and Schoenberg. Furthermore, some of these works (the Webern and the improvisations) are two-handed and polyphonic, therefore constituting a challenging test for models trained on monophonic algorithmic corpora, and making the positive results even more surprising (and encouraging).
The non-tonal and tonal algorithmic melodic (monodic) corpora are distinctive in their information-dynamic structure, and quite different from both random corpora and the Essen folk song tonal corpus employed (Table 1). The greater freedom used in generating the tonal melodic corpus (passing notes were allowed) produced the higher IC of this corpus (4.05) than of the non-tonal (3.79). In turn, both were much higher than the IC (2.46) of the Essen corpus itself, reflecting the greater repetitive predictability of that corpus. Consequently the Essen corpus was not usefully predictive in any of the models of non-tonal music to which it is conceivably relevant (Tables 3-5). (Essen was not appropriate to compare with the polyphonic corpora, since it is a monodic melodic corpus.)
It is apparent from Table 2 that creating polyphonic compositions from the algorithmic melodic corpora dramatically increases their IC, which is expected because the regularities of the serial method are partially removed by the re-sequencing of the pitches which occurs in their formation (as indicated already). Nevertheless, they still contain regularities, as shown by the capacity of pre-training (on themselves) to provide improved models with lower IC. Given the reduction in regularity, and the increase in unpredictability (higher IC) of these polyphonic serial corpora, as indicated by our hypotheses they were much less powerful than the melodic serial corpora from which they were derived in modeling the Webern (Table 3), Schoenberg (Table 4) compositions, and for the relatively high IC piano improvisations (Table 6 vs Table 5) they were devoid of predictive capacity. We therefore focus the remaining discussion on a consideration of the nature of the predictive capacity of the non-tonal melodic corpora.
As mentioned, it is interesting that not only the non-tonal but also the tonal melodic corpora are predictive in some cases; and it is particularly when large melodic intervals are in play that pitch class interval contributes to the optimal IDyOM viewpoint combination (as with the improvisations, the polyphonic corpora and the non-tonal melodic corpus). We next discuss the two compositions and the two improvisation tonality-types in the light of our hypotheses and these two observations; and centered on modeling with the melodic monodic corpora, for reasons just given.
The Webern piece (Table 3) is purely serial. But it contains many short passages which can be interpreted in tonal terms, particularly in the light of jazz harmonies such as the X7♯9 chords, for example F♯ (midi note 54) /C(60) / Fnatural (65), where X is the missing root D. Nevertheless, its enduring impact is of a dynamic non-tonal piece, and so it is consistent with our hypotheses that it is not modeled by Essen, nor can the tonal melodic corpus contribute, but the best model is obtained with the algorithmic non-tonal melodic corpus. In this case, pitch and pitch interval are predictors, but so too is pitch class interval, presumably reflecting the fact that our algorithmic composition method can produce non-uniform distributions of both pitch interval and pitch class interval (the latter because of the randomized transpositions of the row and its transforms, P, RP, I and RI, and the occurrence of many intervals greater than eleven semitones). Even the polyphonic (somewhat re-sequenced) version of this corpus retains some predictive capacity. In sum, our non-tonal corpus has contributed a modeling capacity not previously achieved.
Schoenberg's movement is not serial, but it is by intention non-tonal (though some phrases can readily be viewed in a tonal light). Consistent with our hypotheses, the melodic non-tonal corpus is again substantially predictive, and it removes the need for the pitch class interval viewpoint (interval range in the voices is modest). The tonal corpus is ineffective.
As we move to the piano improvisations (Table 5), we find less rigorously controlled pitch structures performed polyphonically and hence with higher IC. Now for the atonal segments, both the non-tonal and the tonal melodic corpora contribute predictive power, consistent with these facts. This supports our suggestion that the contemporary vernacular of 'atonal' (our referent description for the improvisers' task) or 'non-tonal' music (as we discuss it here) is influenced by serial music and serial ideas, however implicitly. On the other hand, the tonal segments are best modeled by an STM only, and pre-training on any of the corpora is unhelpful. This also is reasonable in terms of our hypotheses since these are the most tonal sections (and they are polyphonic), and of greater flexibility than a tonal composition (as suggested by the IC of 4.95 compared with the 2.46 of Essen), and not driven overtly by any serial considerations.
It is worth considering the influences of pitch class interval further. Table 1 shows that this is important within the non-tonal melodic corpus, but not the tonal. This seems also to be true of the Webern piece (Table 3: which could be pre-trained on the non-tonal melodic corpus to give the optimal model IC 4.21). It remained in place for the STM of the Schoenberg, but was not required after pre-training on the melodic corpora. It was also useful for modeling the improvisations with polyphonic corpora (Table 6: consistent with the greater pitch class interval variability these can contain), but not for models with the melodic corpora (Table 5). It is difficult to extract secure generalizations from these particular observations, but possible implications are that for strongly serial music, and for highly polyphonic music modeled with polyphonic corpora linearized in the way we have used, pitch class interval may be an important viewpoint, providing the pitch interval range is large, so that pitch interval and pitch class interval provide distinct information.
Future work might use single voice non-tonal improvisations and compositions to extend the non-tonal corpus. One could also extract melodic lines from serial/non-tonal compositions (removing harmonic components). But even rigorous serial composition disposes of successive members of a row transform both horizontally and vertically, and multiple transforms may be used simultaneously, as elaborated earlier. Thus a melodic line would not necessarily be closer to the row transforms than the overall sequence of notes in a harmonic performance. However, the difficulty in analyzing a harmonic set from a melodic (single strand) perspective is that the notes of a chord may not be struck in the order specified by the current row transform. Most fundamental is the need for an information-theoretic approach to harmonic analysis, to complement the melodic analytic approach. A vectorial harmonic viewpoint provides a possible approach.
In tonal works, the parameters PitchClass and PitchClassInterval could be recoded each time there is a modulation, better representing the statistical impact of modulation. By extension, the P-RP-I-RI forms could also be separated for IDyOM analysis, and the transpositions also transformed even in the non-tonal music. To the extent a piece contains serial structure, this should be most represented by the PitchClassInterval parameter, and hence captured by a model using it.
The positive results with the non-tonal corpora support previous evidence that non-tonal structure can be perceptually salient (Dibben, 1994; Durrant et al., 2009; Krumhansl et al., 1987) and will eventually permit theoretically-informed cognitive experiments on listeners' detection of unexpected events, and hence tension and resolution (Huron, 2006; Meyer, 1956) in non-tonal contexts. In spite of the predominance of tonal music in Western environments, non-tonal influences are active and are of aesthetic and perceptual interest.
The statistical utility of the non-tonal corpora in modeling ecologically valid improvisation also suggests that the general statistical modeling approach, and IDyOM in particular, can be useful in the context of learning upon first exposure the pitch structures of unfamiliar musics, such as those from different tuning systems and cultures. Given that listeners rapidly adapt to novel musical environments (Kessler et al., 1984), it will be interesting to continue to explore such statistical learning of novel musical styles, using our algorithmically generated non-tonal corpora.
NOTES
- Correspondence can be addressed to: Prof. Roger Dean, MARCS Institute, Western Sydney University, Locked Bag 1797, Penrith, NSW 2751, Australia. roger.dean@westernsydney.edu.au
Return to Text - The IDyOM software is available here: https://code.soundsoftware.ac.uk/projects/idyom-project
Return to Text - The non-tonal corpus benefited very slightly from pre-training on the tonal corpus (pieces 7-12) but this effect disappeared with pre-training on the full tonal melodic corpus.
Return to Text
REFERENCES
- Brindle, R. S. (1966). Serial composition. Cambridge: Cambridge University Press.
- Chew, E. (2005). Regards on two regards by Messiaen: Post-tonal music segmentation using pitch contexdistances in the spiral array. Journal of New Music Research 34(4), 341-54. http://dx.doi.org/10.1080/09298210600578147
- Chordia, P., Sastry, A., & Şentürk, S. (2011). Predictive tabla modelling using variable-length markov and hidden markov models. Journal of New Music Research 40(2), 105-18. http://dx.doi.org/10.1080/09298215.2011.576318
- Dean, R. T. (2014). The serial collaborator: A meta-pianist for real-time tonal and non-tonal music generation. Leonardo 47(3), 260-61. http://dx.doi.org/10.1162/LEON_a_00769
- Dean, R. T., Bailes, F., & Drummond, J. (2014). Generative structures in improvisation: Computational segmentation of keyboard performances. Journal Of New Music Research, no. ahead-of-print: 1-13.
- Dibben, N. (1994). The cognitive reality of hierarchic structure in tonal and atonal music. Music Perception 12(1), 1-25. http://dx.doi.org/10.2307/40285753
- Durrant, S., Hardoon, D. R., Brechmann, A., Shawe-Taylor, J., Miranda, E. R., &. Scheich, H. (2009). Glm and svm analyses of neural response to tonal and atonal stimuli: New techniques and a comparison. Connection Science 21(2-3), 161-75. http://dx.doi.org/10.1080/09540090902733863
- Forte, A. (1973). The structure of atonal music. New Haven: Yale University Press.
- Forte, A. (1978). Schoenberg's creative evolution: The path to atonality. Musical Quarterly, 133-76. http://dx.doi.org/10.1093/mq/LXIV.2.133
- Forte, A. (2002). Olivier Messiaen as serialist. Music Analysis 21, 3-34. http://dx.doi.org/10.1111/1468-2249.00148
- Hunter, D. J. & Von Hippel, P. T. (2003). How rare is symmetry in musical 12-tone rows? The American Mathematical Monthly 110(2), 124-32. http://dx.doi.org/10.2307/3647771
- Huron, D. 2006. Sweet anticipation. Cambridge, MA: MIT Press.
- Kessler, E. J., Hansen, C., & Shepard, R. N., (1984). Tonal schemata in the perception of music in Bali and in the West. Music Perception 2(2), 131-56. http://dx.doi.org/10.2307/40285289
- Krumhansl, C. L. (1990). Cognitive foundations of musical pitch. New York: Oxford University Press, USA.
- Krumhansl, C. L., Sandell, G. J., & Sergeant, D. C. (1987). The perception of tone hierarchies and mirror forms in twelve-tone serial music. Music Perception 5(1), 31-77. http://dx.doi.org/10.2307/40285385
- Lalitte, P., Bigand., E., Kantor-Martynuska, J., & Delbé, C. (2009). On listening to atonal variants of two piano sonatas by Beethoven. Music Perception 26(3), 223-34. http://dx.doi.org/10.1525/mp.2009.26.3.223
- Meyer, L. B. (1956). Emotion and meaning in music. Chicago: University of Chicago Press.
- Pearce, M. T. (2005). The construction and evaluation of statistical models of melodic structure in music perception and composition. Thesis, City University, London.
- Pearce, M. T. & Wiggins, G. A. (2006). Expectation in melody: The influence of context and learning. Music Perception 23, 377-405. http://dx.doi.org/10.1525/mp.2006.23.5.377
- Pearce, M.T. & Wiggins, G. A. (2012). Auditory expectation: The information dynamics of music perception and cognition. Topics in Cognitive Science 2012, 1-28. http://dx.doi.org/10.1111/j.1756-8765.2012.01214.x
- Schaffrath, H. (1995). The Essen Folksong Collection. D. Huron (Ed.), Stanford, California: Center for Computer Assisted Research in the Humanities.
- Temperley, D. (2007). Music and probability. Cambridge, MA: MIT Press.
- Todd, R. L. (1978). Retrograde, inversion, retrograde-inversion, and related techniques in the masses of Jacobus Obrecht. The Musical Quarterly 64(1), 50-78.