THE highly influential theory of aesthetic response by Berlyne (1974) proposed a relationship between liking for artistic stimuli, such as musical melodies, and what he termed their 'collative' properties, which are the informational properties of a stimulus: for instance, its degree of familiarity or complexity. A large number of studies have investigated how musical preferences can be explained in terms of the complexity, originality, or novelty of the melodies (or other artworks) in question (e.g., Burke & Gridley, 1990; North & Hargreaves, 1995, 1999; Radocy, 1982; Simonton, 1980, 1984, 1994, 1995). These studies have tended to support Berlyne's claim that there should be what he called an 'inverted-U relationship' between liking and complexity. However, the actual measurement of the complexity has been difficult since it is intrinsically related to how listeners perceive music, rather than merely quantifying the information carried out by the symbols used to encode music.
In the research stream originated by Berlyne, the assessment of complexity relied on information theory, where the greater the degree of uncertainty it contains, the greater the amount of information conveyed via the music (Shannon & Weaver, 1949). Several empirical studies carried out in the 1960s and 1970s have employed variations of the information-theoretic approach to measure melodic complexity, and these have tended to support the proposed inverted-U relationship between this factor and various measures of preference (e.g., McMullen, 1974; Simon & Wohlwill, 1968; Steck & Machotka, 1975; Vitz, 1966). This approach continued well into late eighties and nineties (Balkwill & Thompson, 1999; for instance, Katz, 1994; Marsden, 1987; Shmulevich, Yli-Harja, Coyle, Povel, & Lemström, 2001). Most of these studies relied on a handful of examples, with one noteworthy exception by Simonton (1984), who analysed the first six notes of 15,618 classical music themes by tallying the probability of occurrence of each of the successive tone-pairs contained within a theme relative to their probability of occurrence within the repertoire as a whole. This score was found to be related to an index of popularity, and the resulting relationship conformed closely to the inverted-U function predicted by Berlyne's theory.
After the 1980s, the interest in complexity was seen as a by-product of understanding the cognitive processing of music, which explained how melodic perception is influenced by regularities in pitch structures (Castellano, Bharucha, & Krumhansl, 1984; Kessler, Hansen, & Shepard, 1984; Oram & Cuddy, 1995), including tonality or more precisely the hierarchical structure of pitch-classes (Krumhansl, 1990), proximity of tones of successive pitches (Schellenberg, 1997), and even implied harmony (Povel & Jansen, 2002). Similarly, the regularities in the temporal domain of music (temporal hierarchy, patterns, and syncopation) have also been the subject of several perceptual studies (e.g., Desain & Honing, 1989; Fitch & Rosenfeld, 2007; Gómez, Melvin, Rappaport, & Toussaint, 2005; Toiviainen & Eerola, 2006). In short, melodies which form clear expectancies that are clearly structured in terms of their tonal, intervallic, and rhythmic properties tend to be easier to reproduce and recognize, and are also judged by listeners as being less complex. These perceptual principles were incorporated into a new stream of models of melodic complexity (Eerola, Himberg, Toiviainen, & Louhivuori, 2006) that used the findings of melodic expectations to estimate complexity. At the same time, models utilizing information-theoretic principles also underwent similar change since they started to incorporate statistical regularity representing long-term knowledge of music (Pearce, 2005; Pearce, Ruiz, Kapasi, Wiggins, & Bhattacharya, 2010). More recently, other ways of quantifying perceptual complexity of melodies have also been proposed based on various underlying principles, such as power law (Beauvois, 2007), multi-scalar structural change (Mauch & Levy, 2011) and signal compression (Marin & Leder, 2013). However, these latest two estimations of complexity go beyond the simple notion of melodic complexity, since their purpose is to gauge the complexity of acoustic signals.
While interest in musical complexity has been constant during the last 30 years, the reasons for exploring it have evidently varied. After the initial interest in the collative properties of the stimulus leading to interest, novelty, and preference, the later wave of interest was to gain insights into perceptual processes that involved comprehending or producing melodies. In other words, melodic complexity has potential as a diagnostic tool for determining where the unexpected events in melodies occur, or what kind of aspects of melodies (pitch combinations, hierarchies, sequential order, etc.) are more important for parsing together melodic structures (as measured by tasks involving similarity ratings, recall of melodies, etc.). A number of studies have explored the malfunctions in processing (Peretz & Hyde, 2003; Tillmann et al., 2011) or producing melodies (Hutchins & Peretz, 2012), which provides even more specific area of application for models of melodic complexity. To date, computational estimations of melodic complexity and the aspects of processing difficulties have only been rarely connected (Omigie, Pearce, & Stewart, 2012).
Aim
The present research attempts to compare two main types of models for melodic complexity: one based on rule-based quantification of expectancy violations and another based on probabilities of musical events. Both have been previously proposed (Eerola & North, 2000a; Pearce & Wiggins, 2004) and combined (Eerola et al., 2006).
Materials and Models
A number of existing datasets were utilized to evaluate the two types of models of melodic complexity. First, these datasets are briefly described, then we turn to the explanations of the models. The music datasets and model predictions are available at http://hdl.handle.net/1811/77849.
Datasets
At least seven published studies exist which have collected overall static ratings of the complexity of melodies (see Table 1). These studies span three decades: none contains a substantial number of stimuli, and the ways in which the melodies have been created, and the complexity ratings collected, may be slightly discrepant between the studies. Nevertheless, such a motley collection of data may serve for a useful purpose in assessing various models of melodic complexity. At the very least, an adequate model explaining all these datasets will already have demonstrated robustness, since the datasets contain different kinds of music, participants from different countries and most likely other practical differences (interface, language, or wording of the instructions). Four of the datasets deal with isochronous melodies (D1-D4) and only three have rhythmical variations in the melodies (D5-D7). In this respect, D7 is exceptional in this context of Western melodies, since the melodies differ particularly in terms of rhythmic structures as they consist of African folk songs.
| Abbr | Description | N | Ratings (n) | Reference |
| D1 | Isochronous and artificial | 32 | USA (120) | Cuddy, Cohen, & Mewhort (1981) |
| D2 | Isochronous variants of Frère Jacques | 6 | SWE (19) | Lindström (2006) |
| D3 | Isochronous 12-tone tonerows | 20 | CAN (16) | Schmuckler (1999) |
| D4 | Isochronous simple melodies | 20 | CAN (16) | Schmuckler (1999) |
| D5 | Artificial and real (pop) melodies | 31 | UK (56) | Eerola & North (2000b) |
| D6 | Folk melodies from Essen collection | 52 | FIN (36) | Eerola et al. (2006) |
| D7 | African melodies, rhythmically varied | 44 | FIN (36) | Eerola et al. (2006) |
In most cases, only the mean ratings have been available for analysis; hence, it is possible neither to estimate the reliability of the ratings nor to use deviation as a more refined source of information in the analysis. When several types of participants (non-musicians, musicians) have given responses, the non-musician data is used here to minimise the effects of expertise. The mean ratings of melodic complexity from the different datasets have been rescaled between 0 and 1 within each dataset to eliminate the differences in the scales in these experiments. The melodies utilized in these datasets have been encoded as MIDI files for the analysis.
Models
Two types of models are detailed here: one based on expectancy-violation and the other on information-theory. The first has its roots in simple implementation of a few expectancy-violation rules (Eerola & North, 2000), which later was refined and evaluated more formally (Eerola et al., 2006). The second type is based on statistical properties of note events in music, which are combined with statistical regularities derived from corpus analysis of music, and finally summarized with information-theoretic measures.
Expectancy-violation Models
A version of the expectancy-violation model (EV) has already been detailed in Eerola et al. (2006), and also documented in Eerola & Toiviainen (Eerola & Toiviainen, 2003), which offers the model (EV8 for eight principles) as a Matlab function, openly available online 1.
In a nutshell, EV8 consists of eight principles, which are linearly combined to produce an overall estimation of the complexity of the melody. Principles 1-4 relate to pitch, 5-8 to rhythm, and they have been inspired by perceptual work in processing melodic and temporal expectations in music. The principles can be briefly summarized as follows:
- (1) Pitch proximity captures the size of the intervals (larger intervals imply complexity), which is known to be a central aspect of melodic expectancies (Schellenberg, 1997; von Hippel, 2000). This is simply calculated as the average interval size in semitones.
- (2) Tonal ambiguity indexes the stability of the pitch-classes within the key (unstable tones imply complexity). The stability of pitch-classes is taken from empirically derived values (Krumhansl & Kessler, 1982) that are weighted by duration accent (Parncutt, 1994). The inverse of the mean stability is taken to be the index of tonal ambiguity. This principle assumes that the melody has been referenced to a common key (C major or minor), which is carried out here by the Krumhansl-Schmuckler key-finding algorithm (Krumhansl, 1990).
- (3) Entropy of the pitch-class distribution measures the variability of the pitch-alphabet by calculating the entropy of the pitch-class distribution (the exact details of these calculations are addressed later in the section, where the information-theoretic models are explained).
- (4) Entropy of the interval distribution is similar to the third principle, except that this focusses on first-order interval distribution rather than pitch-classes.
- (5) Entropy of the duration distribution is a measure of the variability of the duration palette in the melody (the less homogeneous this palette is, the higher the complexity).
- (6) Note density quantifies how many notes per second the melody contains (with more notes, the melody is assumed to be more complex, which is related to the motor-limitations of performance and to the span of the short-term memory in general).
- (7) Rhythmic variation is the overall deviation of the note durations where higher variance suggests higher complexity (Fitch & Rosenfeld, 2007).
- (8) Metrical accent is a measure of phenomenal accent asynchrony where higher values indicate higher complexity (Fitch & Rosenfeld, 2007).

Figure 1. Three melodic extracts from the Essen collection to demonstrate expectancy-violation principles (A: erk0470, B: italia05, and C: Oestr022).
The differences between the principles can be illustrated with three examples taken from the Essen collection, all of which also belong to the D6 dataset. The notation and identities of these extracts are shown in Figure 1 and the extracted principles in Table 2. Melody A consists almost entirely of quarter notes: the tonal structure has low ambiguity, and successive pitches are mainly scale steps. The rhythmic structure of melody B is more complicated than that in melody A, but it has an otherwise similar melodic range and tonal structure. Melody C spans a large range, and therefore also contains large melodic skips and is varied in terms of note durations. Even though the differences in the apparent complexity of these examples is not immense, together they are able to show how the principles index subtle differences between the melodies. In terms of pitch skips, melody A sports the smallest (1.44 semitones on average), and melody C the highest (3.52).
| Melody | |||
| Principle | A | B | C |
| 1 Pitch proximity | 1.44 | 1.68 | 3.52 |
| 2 Tonal ambiguity | -1.64 | -0.65 | -0.75 |
| 3 Entropy of the pitch-class distribution | 0.58 | 0.58 | 0.64 |
| 4 Entropy of the interval distribution | 0.44 | 0.49 | 0.76 |
| 5 Entropy of the duration distribution | 0.14 | 0.25 | 0.31 |
| 6 Note density | 2.28 | 4.32 | 4.09 |
| 7 Rhythmic variation | 0.28 | 0.55 | 0.35 |
| 8 Metrical accent | -0.03 | -0.01 | -0.01 |
Melody A also has the lowest entropies on pitch, interval and duration distributions, note density and rhythmic variation. The differences between melodies B and C lie in pitch proximity, and entropies of all distributions, where melody B has lower values, yet it has higher rhythmic variation and note density than Melody C. Although previous studies have given us clues as to the relative importance of these principles to our perceptual estimations of complexity Eerola et al. (2006), the remainder of this study will assess this particular question in detail.
For full technical details, see either Eerola et al. (2006) or the function details in MIDI toolbox (Eerola & Toiviainen, 2003). This model, abbreviated here as EV8 (Expectancy-violation model with 8 principles), has several limitations such as being able only to estimate complexity of a monophonic music (melody lines) and perhaps suffering from over-fitting since it was initially developed to predict complexity in D5 (Eerola & North, 2000) and later D6 and D7 (Eerola et al., 2006). In addition, the principles contained in this formulation of the model consist of information-theoretic predictors (principles 4-6) that could be argued to be conceptually different from the other principles that are based on averaging indices related to perceptual qualities of notes. To clarify this distinction, the contribution of the individual principles will be critically evaluated with additional datasets, and an attempt will be made to keep information-theoretic and expectancy-violation principles conceptually separate.
Information-theoretic models
The statistical properties of the music form an important part of the expectedness, and thus the complexity. The simplest way to investigate these is to tap into the raw distribution of events in music such as pitch-class, interval, and duration distribution. Pitch-class distribution has 12 states (C, C♯, D, … B) and presumes that the frequency of occurrence of tones takes place within a key context, requiring key-finding for realigning the pitches before meaningful counting of the pitch-classes can be made. Interval distributions simply code the size of the successive pitches in semitones, in this case yielding 25 states (-12, -11,…+11, +12) when the largest interval is constrained to an octave. This distribution is not dependent on the key. Duration distributions require a form of binning of note durations, since durations are not necessarily naturally classified as distinct states. It is common to transform the raw durations (in beats) by using log-transform and then classify these into 9 categories, with the following bin centers:
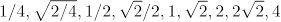
The raw distributions of note events are weighted by durations of the tones, using a duration accent, which represents the decay of the tones in echoic memory (Parncutt, 1994), and gives added salience to longer tones whilst reducing the weight of short tones.
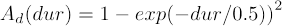
These distributions can be easily extended into higher order statistics. For pitch-classes, one can tally how often the successive pitch-classes occur in a melody. These are known as pitch-class transitions or second-order pitch-class distributions. For simplicity, we call these pitch-class bigrams (PC2). We may also compute even more specific sequences of pitch-classes: trigrams (three successive pitch-classes, PC3), 4-grams (PC4), and 5-grams (PC5) and so on. Whereas the low-order distributions are generic, the high-order distributions tend to be specific, and also sizable (PC5 has 125, that is, 248,832 elements). The same operation can be carried out for successive streams of intervals (IV2, IV3, etc.), although the ensuing distributions are typically extremely sparse (5-gram distribution has nearly 10 million elements, 255, out of which 99.6% are empty if the distribution has been established with 6,236 melodies from the Essen collection). All probability distributions are set to have a sum of 1.
Since music is organized in highly regular ways concerning these probability distributions, these low-order distributions are rather similar across cultures and musical styles (Huron, 2001). Moreover, the empirical ratings of stability of pitch-classes (Krumhansl, 1990) bears high similarity to pitch-class distributions in actual music (Huron, 2001; Järvinen, 1995). To contextualize the distributions within the confines of musical styles, existing regularities should probably be included when accounting for complexity. The simplest way to do this is to combine the distribution p of a melody with a typical, representative distribution P of music in a collection. In this case, we first resort to the Essen collection of folk music for convenience, since it provides an easy access to 6,236 melodies (Schaffrath, 1995) 2 , but of course other available collections (e.g., Bach chorales 3, and other collections 4) could be used. We will explore the role of alternative collections to the performance of the models in the results section.
The combination of the probability distribution in the melody p and the underlying probabilities P can be done simply by summing them whilst weighting the global distribution P with an appropriate constant w. Finally, we may estimate the resulting complexity C of the distribution by calculating the classic Shannon-Weaver entropy H of the summed distribution,
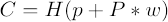
where H is
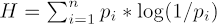
and is p is distribution of states pi in the melody, P the underlying probabilities, and w the weighting parameter. In this analysis, w was heuristically set to be
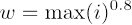
where max(i) is the maximum of states in the distribution. To refer back to the three music examples provided earlier (Figure 1), the basic version of the information-theoretic model would characterize these melodies in a fashion that ranks them from simple (melody A) to complex (melody C), as indicated by the entropies of the selected distributions provided in Table 3. For each distribution, entropy provides an increase in complexity from melody A to B to C. However, this pattern is broken in one representation (PC1), where the melody C is less complicated than B. In this particular case, the pitch-class distribution of melody C uses a more varied palette of pitches than melody B but when key estimation is used to align the reference distribution, the best fitting key for melody B is actually E minor (r=0.71) rather than C major (r=0.69), which creates a composite profile of p and P that is more complicated than the one that would have resulted without transposition. This exception aside (which attests to the vulnerability of auxiliary operations such as key finding), the information-theoretic measures seem to offer a sensible way to index the complexity of the melodies.
| Melody | |||
| Principle | A | B | C |
| PC1 | 0.637 | 0.722 | 0.680 |
| IV1 | 0.553 | 0.596 | 0.791 |
| DU1 | 0.665 | 0.707 | 0.755 |
| PC3 | 0.750 | 0.754 | 0.760 |
| IV3 | 0.635 | 0.637 | 0.642 |
Since there are several ways to implement the information-theoretic models, the possible variations are explored in the results. This will assess the impact of statistical order, the representation, the measure utilized, and also the alternative underlying distributions to the predictive rate of the information-theoretic models.
Results
The expectancy-violation models are examined first, starting with the analysis of principle redundancy in the original model and proceeding to optimize the model by means of principle reduction. This section is followed by analyses of the information-theoretic models in terms of the principle variants (order, representations, measures, and underlying distributions) and also concludes with model optimization. In the final section, the optimal versions of each type of model are compared.
Optimization of Expectancy-Violation Models
In the name of model parsimony, it might be prudent to construct a simpler model since not all of the principles have fully contributed to the model in the past (Eerola et al., 2006). It is also worth noting, that in Eerola et al. (2006), 10 melodic principles were first extracted from a large collection of melodies (6,236 melodies from the Essen collection) and subjected to principal component analysis. This operation identified four components (labeled as hierarchical structure, pitch, rhythm, and periodic structure) that explained 84.6% of the variance in the data. This operation was used to argue that the selected components for the models were feasible and addressed separate aspects of music, even if no significant trimming of the principles was carried out. This remains to be done here with the help of more extensive datasets.
In the datasets D1-D7, there are 205 observations in total. This allows us to enter 10 variables for a regression analysis if we use the most conservative estimate about the ratio of observations to variables (10:1, see Hair, Tatham, Anderson, & Black, 2006). In this case, we enter the 10 melodic principles used in the previous study (Eerola et al., 2006) in a simple regression. To avoid over-fitting, we carry out 5-fold cross-validation of the model. The musical predictors have been normalized within datasets before the analysis (M=0, SD=1). This analysis yields a moderate fit, R2adj=.416, F(163,10)=13.31, p<.001, where 3-4 principles (tonal ambiguity, entropy of pitch-class distribution, entropy of duration distribution, and pitch proximity) contribute significantly to the model prediction (Table 4). The final column in Table 4 refers to the unique proportion of variance explained by the principle (semi-partial correlation, sr2). The normalized beta coefficients (ß) for the key principles operate in the assumed direction (i.e., they are positive).
| Principle | ß | p | sr2 |
| 1 Note density | -0.003 | 0.9034 | 0.000 |
| 2 Tonal ambiguity | 0.125 | 0.0001 | 0.098 |
| 3 Metrical accent | 0.013 | 0.5115 | 0.002 |
| 4 Entropy of pitch-class distribution | 0.043 | 0.0204 | 0.019 |
| 5 Entropy of interval distribution | 0.025 | 0.2124 | 0.005 |
| 6 Pitch proximity | 0.080 | 0.0001 | 0.054 |
| 7 Entropy of duration distribution | 0.050 | 0.0651 | 0.012 |
| 8 Rhythmic variability | 0.008 | 0.7736 | 0.000 |
| 9 Contour similarity | -0.004 | 0.8421 | 0.000 |
| 10 Contour entropy | 0.006 | 0.7588 | 0.000 |
We may formulate two simpler models by choosing the most efficient predictors from this analysis. First, we choose the best four predictors: tonal ambiguity, proximity, the entropy of duration distributions, and the entropy of the pitch-class distributions. This yields a somewhat better model than the linear combination of the 10 principles: R2adj=.447, F(200, 4)=42.19, p<.001 (see Table 5 for details). In order to keep the expectancy-violation model clear of the information-theoretic principles, we can simply choose three efficient principles that also represent the main principal components in past analysis (PCA 1 Tonal ambiguity, PCA 2 Pitch proximity, PCA 3 Rhythmic variability). This yields R2adj=.407, F(201, 3)=47.6, p<.001, which is marginally inferior (-0.9%) in terms of the variance explained, but somewhat more elegant in terms of model simplicity, since it contains only three predictors, and none is related to information-theory. Both simplified models are summarized in Table 5.
| Predictor | ß | p | sr2 |
| EV4 | R2adj=.447 | ||
| Tonal ambiguity | 0.116 | <0.0001 | 0.182 |
| Pitch proximity | 0.099 | <0.0001 | 0.131 |
| Entropy of duration distribution | 0.044 | <0.01 | 0.021 |
| Entropy of pitch-class distribution | 0.049 | <0.001 | 0.032 |
| EV3 | R2adj=.407 | ||
| Tonal ambiguity | 0.123 | <0.0001 | 0.204 |
| Pitch proximity | 0.107 | <0.0001 | 0.158 |
| Rhythmic variability | 0.036 | 0.055 | 0.011 |
The optimal predictors largely confirm what we already know about melodic violations: mainly, that tonality and pitch proximity are highly influential (Krumhansl et al., 2000; Schellenberg, 1997). The central role of pitch proximity has also been confirmed in another empirical study of melodic complexity. The observation by Beauvois (2007)—that 1/fß power law is related to complexity—seems to be tapping mainly into pitch proximity, because in his dataset the complexity ratings were almost perfectly correlated with the standard deviation of the interval sizes of the melodies (p. 253).
However, we will leave comparison of the three formulations (EV8, EV4, EV3) of the expectancy-violation models to a later section.
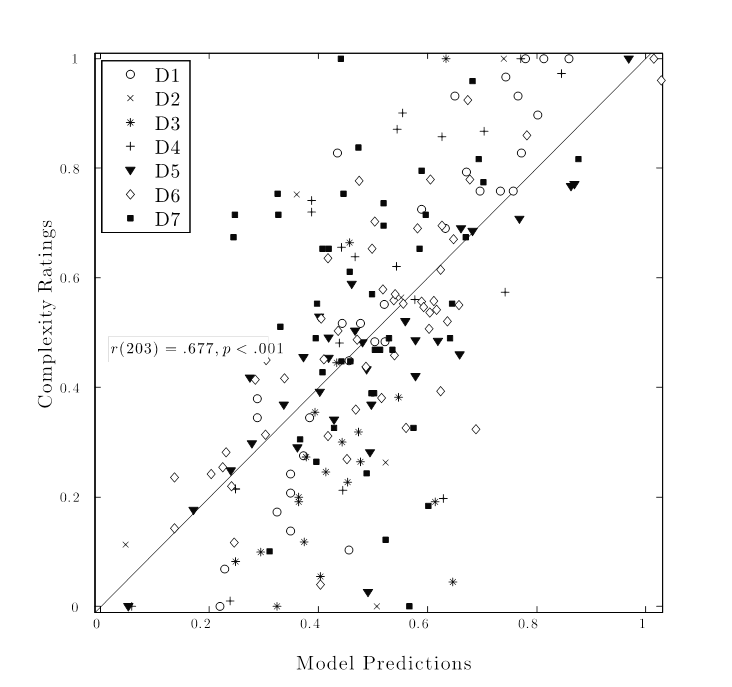
Finally, a visualization of the predictions from the best performing model (EV4) across the datasets is a useful way to examine whether particular datasets or melodies are behaving oddly in this modelling exercise (see Figure 1). As expected from the regression results, a high linear relationship between the ratings and the model predictions exist with fairly evenly spread distribution of individual melodies from each collection across the diagonal. The problematic cases, being the furthest away from the diagonal, indicate either complexity that was not picked up by the models (examples considerably above the diagonal) or too sensitive estimation of complexity (the examples below the diagonal). As far as the datasets go, D7 (black squares) can be identified for both errors, mainly for underestimating the complexity. For instance, the melody at the top of the plot with rated complexity of 1.0 and estimated complexity of 0.47 is the extreme example, although several less severe errors with the same trend can be identified in the upper leftmost quadrant of the figure. These errors suggest that the melody contains aspects of complexity that are not addressed by the model but are clear to the participants. In these cases, these are likely to be attributable to the rhythmic and temporal aspects of the music, since the dataset D7 contains highly syncopated African folk songs. Despite these peculiarities, the overall pattern supports the use of linear models in constructing optimal measures of melodic complexity.
Optimization of Information-Theoretic Models
In information-theoretic models, one can alter the order of the statistical distribution (unigram, 2-gram, 3-gram…), the reference set P, and the method of comparison of the two distributions. This changes how specific the model is for both the reference and melodic properties. First, the order of the statistics was examined by taking the orders of 1 to 5 for pitch-class (PC1-5) and interval distribution (IV1-5). Since duration distribution is considerably sparser than pitch-class and interval distribution, and half of the datasets (D1-4) do not contain any variance in durations, higher order duration distributions were not included in the analysis. The first-order version of the duration distribution (DU1) was kept in the analysis for the sake of comparison.
| Model | D1 | D2 | D3 | D4 | D5 | D6 | D7 | Median |
| PC1 | 0.64 | 0.96 | - | 0.61 | 0.75 | 0.32 | 0.07 | 0.61 |
| PC2 | 0.68 | 0.97 | 0.21 | 0.80 | 0.77 | 0.38 | 0.04 | 0.68 |
| PC3 | 0.72 | 0.91 | 0.20 | 0.93 | 0.81 | 0.54 | 0.18 | 0.72 |
| PC4 | 0.69 | 0.89 | 0.26 | 0.91 | 0.76 | 0.50 | 0.18 | 0.69 |
| PC5 | 0.65 | 0.90 | 0.28 | 0.87 | 0.73 | 0.48 | 0.15 | 0.65 |
| IV1 | 0.21 | 0.02 | 0.53 | 0.84 | 0.83 | 0.62 | 0.06 | 0.53 |
| IV2 | 0.34 | 0.43 | 0.41 | 0.91 | 0.90 | 0.65 | 0.12 | 0.43 |
| IV3 | 0.56 | 0.79 | 0.33 | 0.92 | 0.91 | 0.65 | 0.17 | 0.65 |
| IV4 | 0.64 | 0.81 | 0.28 | 0.90 | 0.88 | 0.62 | 0.17 | 0.64 |
| IV5 | 0.58 | 0.79 | 0.28 | 0.87 | 0.84 | 0.60 | 0.15 | 0.60 |
| DU1 | - | - | - | - | 0.39 | 0.16 | 0.21 | 0.16 |
| Median | 0.64 | 0.85 | 0.28 | 0.89 | 0.81 | 0.54 | 0.15 | 0.64 |
In Table 6, a few variants of the models in particular datasets cannot be evaluated since the distributions are uniform (isochronous melodies in D1-4 have uniform note durations, and tone rows in D3 have flat pitch-class distributions). These exceptions aside, overall the models provide a decent estimate of complexity, the overall median correlation being r=.61. The order of the statistics seems to have a small but consistent impact on the results. In most cases (9 of 14 models), the 3-grams produce slightly better fit than the lower and higher order variants. The pattern is similar across interval and pitch-class distributions and datasets. The lowest (PC1, IV1) and highest order (PC5, IV5) distributions perform clearly worse than 3-grams. This could be interpreted as indicating that the 3-grams offer the most suitable compromise between being too generic or too precise. Pitch-class distributions deliver slightly higher fit (median r 0.72 for PC3) to the ratings than the interval distributions (0.64), although this difference may come with a price. If we bear in mind that pitch-class distributions were not always informative (e.g., in dataset D3) and they need a reliable key estimation in order to be computed, the interval distributions may actually be simpler and thus more parsimonious than the models based on pitch-classes. Such differences between the models will be analytically evaluated later.
To provide a more comprehensive evaluation of the information-theoretic models, the reference distribution P, which was initially derived from the Essen folk song collection, was altered. Alternatives were derived from the vocal lines in: (1) Bach chorales (n = 15); (2) pop song melodies (n = 214); (3) 2-grams in classical music by Simonton (1984) (n = 15,618); and (4) by Youngblood (1958), and (5) pitch-class distributions in Schubert songs (Knopoff & Hutchinson, 1983). The latter three distributions are available in the 'refstat' function in the MIDI Toolbox (Eerola & Toiviainen, 2003).
The analysis of the models with these alternative reference distributions provided, however, marginal improvement. If we look at the median correlations aggregated across the seven datasets, the differences with the alternative distributions are relatively small (±0.02). For 1-grams, replacing the distributions derived from the Essen collection with those derived from classical music resulted in marginal improvements (PC1_Schubert = 0.63). Similarly in 2-grams (PC2_Simonton = 0.70, PC2_Youngblood = 0.67). In 3-grams, probabilities derived from Bach chorales yielded identical results (PC3_Bach = 0.72) whereas 3-grams derived from Top10 hits yields a lower fit (PC3_pop = 0.54). This pattern was similar for interval distributions, where Top10 hits (IV3_pop =0.58) did not quite reach the results obtained by the Essen collection (IV3 = 0.65) and the Bach chorales provided a lower fit (IV3_Bach=0.53). In sum, this cursory exploration of the alternative reference distributions suggested that no dramatic improvements could be obtained with them, but also that the information-theoretic models do tolerate changes to references distributions in a satisfactory manner.
Finally, several alternative information-theoretic measures for comparing the distributions p and P were carried out. These were all based on Mutual Information (MI), which captures the dependence of the two distributions (MacKay, 2003).
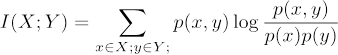
Here the idea is to capture the degree that the distribution p differs from the reference distribution P by assessing the inverse of the mutual information. This formulation, however, did not yield a better estimation of melodic complexity: the median r across all datasets was 0.15, lower than in the estimation based on the entropy of the summed distributions. Neither did any variants of the mutual information estimation yield a better fit (Complex domain mutual information, r = .33, Spearman's p, r = .27, and Kernel canonical correlation analysis, r = .36). All four variations of the distribution comparisons were carried out using ITE Toolbox (Szabó, 2014).
Finally, it is prudent to optimize the information-theoretic model in a similar way to that carried out for the expectancy-violation models, by combining the best principles of these variants. In this case, a linear combination of PC3 and IV3 was constructed (this model is called IT2 for Information-Theoretic model with two predictors). Together these two variables account for 32% of the variance in the complexity ratings (R2adj=.321, F(202, 2)=49.25, p<.001), where both variables contribute significantly to the model (PC3 ß=.077, p=.0018 and IV3 ß=.088, p=.0003).
At this point, six optimized variants of the expectancy-violation and information-theoretic models have been put forward (three from each). All the proposed models can account for a noteworthy variation in the complexity ratings obtained in separate studies, but what remains to be done is an analytical comparison of the best models.
Model Comparison
The simplest way to describe the model is to look at the performance within the datasets using correlation coefficients (Table 7). If we look at the median correlation across the datasets (the rightmost column), we might conclude that the EV4 is superior since it has the overall highest median correlation (r=.74). PC3 is not, nevertheless, far behind (r=.72) and actually outperforms EV4 on two datasets (D2 and D4). Overall, two datasets, D3 and D7, are consistently more poorly predicted by all models in comparison to other datasets. D3, which consists of 20 isochronous twelve-tone sequences, is perhaps operating under rather different aesthetic premises. These sequences use each pitch-class once, have no variation in timing, no natural phrasing or tonality, and the random nature of the sequences makes this arguably the most artificial dataset. D7 consists of 44 African melodies, which are particularly rich in terms of metrical and rhythmic structure. Most of the models are not able to pick up the nuances that the temporal structures of the melodies offer. Only the original expectancy-violation model (EV8) is able to capture a part of the difference in the ratings: this is understandable because it has four principles addressing rhythm (entropy of the duration distribution, note density, rhythmic variation and metrical accent), and it was originally constructed to account for the ratings in this dataset.
| Model | D1 | D2 | D3 | D4 | D5 | D6 | D7 | Median |
| EV8 | 0.46 | 0.12 | 0.35 | 0.68 | 0.55 | 0.81 | 0.34 | 0.46 |
| EV4 | 0.91 | 0.53 | 0.46 | 0.74 | 0.83 | 0.80 | 0.18 | 0.74 |
| EV3 | 0.91 | 0.37 | 0.46 | 0.68 | 0.76 | 0.78 | 0.12 | 0.68 |
| PC3 | 0.72 | 0.91 | 0.20 | 0.93 | 0.81 | 0.54 | 0.18 | 0.72 |
| IV3 | 0.56 | 0.79 | 0.33 | 0.92 | 0.91 | 0.65 | 0.17 | 0.65 |
| IT2 | 0.69 | 0.88 | 0.34 | 0.94 | 0.85 | 0.67 | 0.23 | 0.69 |
Overall, the differences between the final six models are fairly subtle and the prediction rate fails to capture the complexity of the models, which can be another criterion for assessing the models. For this reason, analysis of the model parsimony was carried out using Akaike Information Criterion (AIC) (Akaike, 1974). This measure combines the prediction rate (with Residual Sum Squares) and the number of components (K) in the model, and penalizes the more complex models over the simple ones. It may be worth noting here that the two information-theoretic models, IV3 and PC3, have only one component (the principle being calculated), whereas the models optimized with regression all have at least four terms (e.g. IT2, 2 principles, error term + constant in the regression), rendering them more complex.
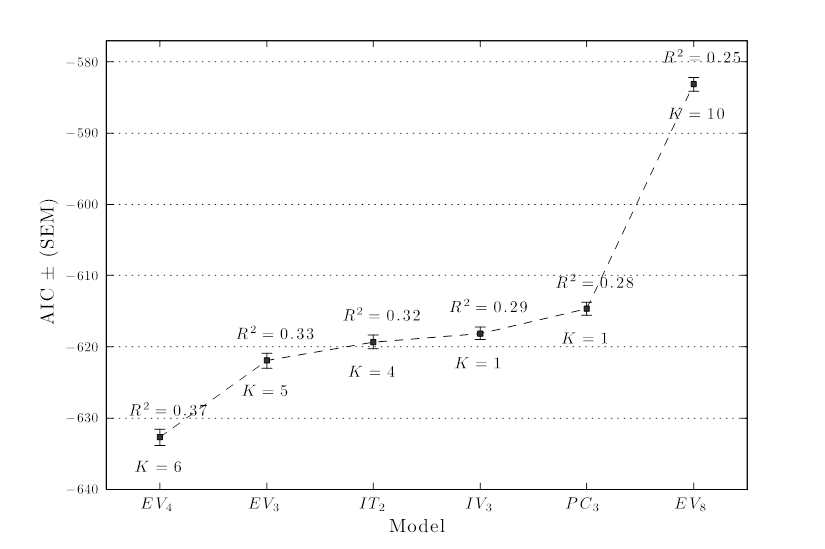
Figure 3. Model parsimony with (AIC) across the models where K refers to the number of model parameters.
For simplicity, this analysis was carried out with all datasets at once, rather than treating each separately, since averaging results across the datasets would not take into account the different number of observations in each. In addition, the calculation of the AIC for each model was replicated 500 times with random selection of the observations to estimate the confidence intervals. Figure 3 displays the AIC results for the six final models, where low AIC indicates a more effective, parsimonious model. K values indicate the number of parameters in the models and the R2 values are provided for each.
This analysis suggests that EV4 may be a good compromise between simplicity and predictive power. Similarly, EV3 is also an efficient model, albeit only slightly better in terms of parsimony than information-theoretic models (IT2, and IV3), which are indistinct with respect to the criterion applied, since they have nearly identical AIC values. It has to be said that the differences between the most optimal models appear to be quite small here, although clearly the model with eight principles and mediocre prediction rate (EV8) is not sufficiently parsimonious in this analysis. However, other selection criteria (such as the Bayesian Information Criterion) might have favored models with fewer principles over the prediction rate. Despite the numerical analysis, the exact need and the application case of such models might be the most important principle for selecting the model, particularly since all top five models provide a reasonable fit to the data. In a case where robustness and simplicity is of paramount importance, IV3 is a lucrative model since it has no parameters, it does not depend on key estimation (unlike most other models), and only has a small degradation in performance (13% of variance explained, taken from Table 7, that is, correlation squared).
Conclusions
Two types of models of melodic complexity were evaluated: one based on violations of expectancies and the other related to redundancy of events in the music. The data comprised seven different datasets consisting of listener ratings of complexity for melodies ranging from artificial sequences to folk from Europe and Africa as well as pop song melodies. The analysis proceeded incrementally: first the overlap in past expectancy-violation models was explored and the number of variables in the models was halved. Similar refinement was carried out for the information-theoretic models, where the order of the n-gram was scrutinized and the third-order statistics for pitch-class and interval representations were taken further. An optimal combination of these two principles was also put forward. This left the final analysis with three variants of each model type, for expectancy-violations models EV8, EV4, EV3, and for information-theoretic models PC3, IV3, and IT3. These models could explain from 21-55% of the variance in the ratings within the datasets, with significant variations across the datasets. The final comparison identified the best models using Akaike Information Criterion, which suggested that the most parsimonious model was EV4. For other models, there was no clear difference between the two model types in terms of performance and simplicity.
The difference between the types of model is theoretically notable but in practical terms subtle, since the rule-based principles are probably heuristics that capture statistical regularities of the music, and vice versa. Moreover, the original formulations of the expectancy-violation model contained information-theoretic calculations of musical content. For information-theoretic models, alternative methods of redundancy estimations and the underlying representations and distributions were explored, but none of these yielded significant improvements to the predictions.
On a critical note, the present research provided a somewhat narrow selection of possible representations for melodies. Both types were based on discrete representations of musical events (pitches, intervals, durations and various derivatives of these), although it would be possible to formulate other types of models based on continuous representation such as melodic contour (Eerola et al., 2006; Schmuckler, 1999) or identification of salient melodic events (Frankland & Cohen, 2004), or implied chords (Povel & Jansen, 2002). The simplicity of the current models could also be seen as an advantage, since it is probable that simpler solutions might have more applicability across different applied contexts.
The nature of data utilized in the study was heterogeneous at best. The datasets vary in terms of instructions given to the participants and, of course, the languages and the interfaces have been different in most cases. More importantly, the participants themselves represent North America, Scandinavia, and the UK, which does not make the study particularly cross-cultural, but may add another source of variance to the data. All datasets consist of relatively small samples (from n=6 to n=52). To apply the results to other types of situations (dynamic ratings of complexity or continuous predictions of expectancy), one must bear in mind that the ratings were static, and thus the whole melody was rated after listening to the music. Such ratings are prone to bias (e.g., recency effect or the peak-end rule), although the actual role of these biases in this kind of context is not known.
Adequate models of melodic complexity may be useful for assessing perceptual processes and production issues involved in music, such as errors made by people suffering from amusia, or for providing insight into performance or memory errors. It is also likely that, if such models are applied across the span of the melody, the fluctuation of the complexity across the melody may identify segment boundaries (Pearce, Müllensiefen, & Wiggins, 2008). However, the simplest application of melodic complexity is to control for complexity in organizing stimuli for other perceptual topics.
NOTES
REFERENCES
- Akaike, H. (1974). A new look at the statistical model identification. IEEE Transactions on Automatic Control, 19(6), 716–723. http://dx.doi.org/10.1109/TAC.1974.1100705
- Balkwill, L. L., & Thompson, W. F. (1999). A cross-cultural investigation of the perception of emotion in music: Psychophysical and cultural cues. Music Perception, 17(1), 43–64. http://dx.doi.org/10.2307/40285811
- Beauvois, M. W. (2007). Quantifying aesthetic preference and perceived complexity for fractal melodies. Music Perception, 24(3), 247–264. http://dx.doi.org/10.1525/mp.2007.24.3.247
- Berlyne, D. E. (1974). The new experimental aesthetics. In D. E. Berlyne (Ed.), Studies in the new experimental aesthetics: Steps towards an objective psychology of aesthetic appreciation (pp. 1–25). Washington: Hemisphere Publishing Co.
- Burke, M. J., & Gridley, M. C. (1990). Musical preferences as a function of stimulus complexity and listeners'sophistication. Perceptual and Motor Skills, 71(2), 687–690.
- Castellano, M. A., Bharucha, J. J., & Krumhansl, C. L. (1984). Tonal hierarchies in the music of North India. Journal of Experimental Psychology: General, 113(3), 394–412. http://dx.doi.org/10.1037/0096-3445.113.3.394
- Cuddy, L. L., Cohen, A. J., & Mewhort, D. J. K. (1981). Perception of structure in short melodic sequences. Journal of Experimental Psychology: Human Perception and Performance, 7(4), 869–883. http://dx.doi.org/10.1037/0096-1523.7.4.869
- Desain, P., & Honing, H. (1989). The quantisation of musical time: A connectionist approach. Computer Music Journal, 13(3), 56–66. http://dx.doi.org/10.2307/3680012
- Eerola, T., & North, A. C. (2000). Expectancy-based model of melodic complexity. In C. Woods, G. B. Luck, R. Brochard, S. A. O'Neill, & J. A. Sloboda (Eds.), Proceedings of the sixth international conference on music perception and cognition (pp. 1177–1183). Keele, Staffordshire, UK: Department of Psychology, Keele University.
- Eerola, T., & Toiviainen, P. (2003). MIDI toolbox: MATLAB tools for music research. Jyväskylä, Finland: University of Jyväskylä.
- Eerola, T., Himberg, T., Toiviainen, P., & Louhivuori, J. (2006). Perceived complexity of Western and African folk melodies by Western and African listeners. Psychology of Music, 34(3), 341–375. http://dx.doi.org/10.1177/0305735606064842
- Fitch, W. Tecumseh, & Rosenfeld, A. J. (2007). Perception and production of syncopated rhythms. Music Perception, 25(1), 43–58. http://dx.doi.org/10.1525/mp.2007.25.1.43
- Frankland, B. W., & Cohen, A. J. (2004). Parsing of melody: Quantification and testing of the local grouping rules of Lerdahl and Jackendoff's A Generative Theory of Tonal Music. Music Perception, 21(4), 499–543. http://dx.doi.org/10.1525/mp.2004.21.4.499
- Gómez, F., Melvin, A., Rappaport, D., & Toussaint, G. T. (2005). Mathematical measures of syncopation. In R. Sarhangi, & R. V. Moody (Eds.), Proceedings of BRIDGES: Mathematical connections in art, music, and science (pp. 73–84). Canada: Banff, Alberta: Canada: Banff, Alberta.
- Hair, J. F., Tatham, R. L., Anderson, R. E., & Black, W. (2006). Multivariate data analysis. US NJ: Pearson Prentice Hall.
- Huron, D. (2001). Tone and voice: A derivation of the rules of voice-leading from perceptual principles. Music Perception, 19(1), 1–64. http://dx.doi.org/10.1525/mp.2001.19.1.1
- Hutchins, S. M., & Peretz, I. (2012). A frog in your throat or in your ear? Searching for the causes of poor singing. Journal of Experimental Psychology: General, 141(1), 76–97. http://dx.doi.org/10.1037/a0025064
- Järvinen, T. (1995). Tonal hierarchies in jazz improvisation. Music Perception, 12(4), 415–437. http://dx.doi.org/10.2307/40285675
- Katz, B. F. (1994). An ear for melody. Connection Science, 6(2-3), 299–324. http://dx.doi.org/10.1080/09540099408915728
- Kessler, E. J., Hansen, C., & Shepard, R. N. (1984). Tonal schemata in the perception of music in Bali and the West. Music Perception, 2(2), 131–165. http://dx.doi.org/10.2307/40285289
- Knopoff, L., & Hutchinson, W. (1983). Entropy as a measure of style: The influence of sample length. Journal of Music Theory, 27, 75–97. http://dx.doi.org/10.2307/843561
- Krumhansl, C. L. (1990). Cognitive foundations of musical pitch. Oxford: Oxford University Press.
- Krumhansl, C. L., & Kessler, E. J. (1982). Tracing the dynamic changes in perceived tonal organisation in a spatial representation of musical keys. Psychological Review, 89(4), 334–368. http://dx.doi.org/10.1037/0033-295X.89.4.334
- Krumhansl, C. L., Toivanen, P., Eerola, T., Toiviainen, P., Järvinen, T., & Louhivuori, J. (2000). Cross-cultural music cognition: Cognitive methodology applied to North Sami yoiks. Cognition, 76(1), 13–58. http://dx.doi.org/10.1016/S0010-0277(00)00068-8
- Lindström, E. (2006). Impact of melodic organization on perceived structure and emotional expression in music. Musicae Scientiae, 10(1), 85–117. http://dx.doi.org/10.1177/102986490601000105
- MacKay, D. J. C. (2003). Information theory, inference, and learning algorithms. Cambridge, UK: Cambridge University Press.
- Marin, M. M., & Leder, H. (2013). Examining complexity across domains: Relating subjective and objective measures of affective environmental scenes, paintings and music. PloS One, 8(8), e72412. http://dx.doi.org/10.1371/journal.pone.0072412
- Marsden, A. A. (1987). A study of cognitive demands in listening to Mozart's quintet for piano and wind instruments, k. 452. Psychology of Music, 15(1), 30–57. http://dx.doi.org/10.1177/0305735687151004
- Mauch, M., & Levy, M. (2011). Structural change on multiple time scales as a correlate of musical complexity. In Proceedings of the 12th International Society for Music Information Retrieval Conference (ISMIR 2011) (pp. 489–494). Miami, US: University of Miami.
- McMullen, P. T. (1974). Influence of number of different pitches and melodic redundancy on preference responses. Journal of Research in Music Education, 22(3), 198–204. http://dx.doi.org/10.2307/3345141
- North, A. C., & Hargreaves, D. J. (1995). Subjective complexity, familiarity, and liking for popular music. Psychomusicology: Music, Mind & Brain, 14(1), 77–93. http://dx.doi.org/10.1037/h0094090
- North, A. C., & Hargreaves, D. J. (1999). Can music move people? The effects of musical complexity and silence on waiting time. Environment and Behavior, 31(1), 136–149. http://dx.doi.org/10.1177/00139169921972038
- Omigie, D., Pearce, M. T., & Stewart, L. (2012). Tracking of pitch probabilities in congenital amusia. Neuropsychologia, 50(7), 1483–1493. http://dx.doi.org/10.1016/j.neuropsychologia.2012.02.034
- Oram, N., & Cuddy, L. L. (1995). Responsiveness of Western adults to pitch-distributional information in melodic sequences. Psychological Research, 57(2), 103–118.
- Parncutt, R. (1994). A perceptual model of pulse salience and metrical accent in musical rhythms. Music Perception, 11(4), 409–464. http://dx.doi.org/10.2307/40285633
- Pearce, M. T. (2005). The construction and evaluation of statistical models of melodic structure in music perception and composition (PhD thesis). Department of Computing, City University, London, UK.
- Pearce, M. T., & Wiggins, G. A. (2004). Improved methods for statistical modelling of monophonic music. Journal of New Music Research, 33(4), 367–385. http://dx.doi.org/10.1080/0929821052000343840
- Pearce, M. T., Müllensiefen, D., & Wiggins, G. A. (2008). A comparison of statistical and rule-based models of melodic segmentation. In J. P. Bello & E. Chew (Eds.), Proceedings of the ninth international conference on music information retrieval (pp. 89–94). Philadelphia, USA: Drexel University.
- Pearce, M. T., Ruiz, M. H., Kapasi, S., Wiggins, G. A., & Bhattacharya, J. (2010). Unsupervised statistical learning underpins computational, behavioural and neural manifestations of musical expectation. NeuroImage, 50, 302–313. http://dx.doi.org/10.1016/j.neuroimage.2009.12.019
- Peretz, I., & Hyde, K. L. (2003). What is specific to music processing? Insights from congenital amusia. Trends in Cognitive Sciences, 7(8), 362–367. http://dx.doi.org/10.1016/S1364-6613(03)00150-5
- Povel, D.-J., & Jansen, E. (2002). Harmonic factors in the perception of tonal melodies. Music Perception, 20(1), 51–85. http://dx.doi.org/10.1525/mp.2002.20.1.51
- Radocy, R. E. (1982). Preference for classical music: A test for the hedgehog. Psychology of Music, Special Issue, 91-95.
- Schaffrath, H. (1995). The Essen folksong collection. In D. Huron (Ed.), Database containing 6,255 folksong transcriptions in the Kern format and a 34-page research guide [computer database]. Menlo Park, CA: CCARH.
- Schellenberg, E. G. (1997). Simplifying the implication-realisation model of melodic expectancy. Music Perception, 14(3), 295–318. http://dx.doi.org/10.2307/40285723
- Schmuckler, M. A. (1999). Testing models of melodic contour similarity. Music Perception, 16(3), 295–326. http://dx.doi.org/10.2307/40285795
- Shannon, C. E., & Weaver, W. (1949). The mathematical theory of communication. Urbana, Illinois: University of Illinois Press.
- Shmulevich, I., Yli-Harja, O., Coyle, E., Povel, D.-J., & Lemström, K. (2001). Perceptual issues in music pattern recognition: Complexity of rhythm and key finding. Computers and the Humanities, 35(1), 23–35. http://dx.doi.org/10.1023/A:1002629217152
- Simon, C. R., & Wohlwill, J. F. (1968). An experimental study of the role of expectation and variation in music. Journal of Research in Music Education, 16(3), 227–238. http://dx.doi.org/10.2307/3344079
- Simonton, D. K. (1980). Thematic fame and melodic originality in classical music: A multivariate computer-content analysis. Journal of Personality, 48(2), 206–219. http://dx.doi.org/10.1111/j.1467-6494.1980.tb00828.x
- Simonton, D. K. (1984). Melodic structure and note transition probablities: A content analysis of 15,618 classical themes. Psychology of Music, 12, 3–16. http://dx.doi.org/10.1177/0305735684121001
- Simonton, D. K. (1994). Individual differences, developmental changes and social context. Behavioural and Brain Sciences, 17(3), 552–553. http://dx.doi.org/10.1017/S0140525X00035925
- Simonton, D. K. (1995). Drawing inferences from symphonic programs: Musical attributes versus listener attributions. Music Perception, 12, 307–322. http://dx.doi.org/10.2307/40286186
- Steck, L., & Machotka, P. (1975). Preference for musical complexity: Effects of context. Journal of Experimental Psychology: Human Perception and Performance, 1(2), 170–174. http://dx.doi.org/10.1037/0096-1523.1.2.170
- Szabó, Z. (2014). Information theoretical estimators toolbox. Journal of Machine Learning Research, 15, 283–287.
- Tillmann, B., Burnham, D., Nguyen, S., Grimault, N., Gosselin, N., & Peretz, I. (2011). Congenital amusia (or tone-deafness) interferes with pitch processing in tone languages. Frontiers in Psychology, 2(120), 10.3389/fpsyg.2011.00120. http://dx.doi.org/10.3389/fpsyg.2011.00120
- Toiviainen, P., & Eerola, T. (2006). Autocorrelation in meter induction: The role of accent structure. The Journal of the Acoustical Society of America, 119(2), 1164–1170. http://dx.doi.org/10.1121/1.2146084
- Vitz, P. C. (1966). Affect as a function of stimulus variation. Journal of Experimental Psychology, 71(1), 74-79. http://dx.doi.org/10.1037/h0022619
- von Hippel, P. T. (2000). Questioning a melodic archetype: Do listeners use gap-fill to classify melodies? Music Perception, 18(2), 139–153. http://dx.doi.org/10.2307/40285906
- Youngblood, J. E. (1958). Style as information. Journal of Music Theory, 2, 24–35. http://dx.doi.org/10.2307/842928