KRAEPELIN (1899/1921) identified five characteristics of sad speech: (1) low overall pitch, (2) small pitch movement, (3) quieter, (4) mumbled articulation, and (5) slower speaking rate. Over the past century, Kraepelin's clinical observations have been confirmed through controlled experimental studies. With regard to small pitch movement, sad vocal prosody is more "monotone" compared with normal voice (Banse & Scherer, 1996; Bergmann, Goldbeck & Scherer, 1988; Breitenstein, van Lancker, & Daum, 2001; Davitz, 1964; Eldred & Price, 1958; Fairbanks & Pronovost, 1939; Huttar, 1968; Skinner, 1935; Sobin & Alpert, 1999; Williams & Stevens, 1972). Wide pitch excursions are associated with high physiological arousal, such as occurs in joy or anger. By contrast, low variability of the fundamental pitch (F0) is characteristic of low arousal, including both sad voice and sleepy voice.
In historical and cross-cultural studies, music-related sadness is one of the most commonly described affects. In his volume De Medicina, the first century Roman physician Aulus Celsus described how "playing soft music" might be used to treat the mental stupor thought to be caused by an excess of black bile—a condition Celsus described by its literal Latin term, melancholia. Similar descriptions of music's ability to evoke or temper sadness can be found in many historical texts spanning many cultures, including ancient Egyptian, Chinese, Hebrew, Persian, Arabic, and Sanskrit sources. Apart from historical sources, there also exist both ethnographic and empirical descriptions of grief- or sadness-related musical experiences in many cultures. Laments, sorrow songs, dirges, elegies, and mourning-song traditions are evident around the world, especially in eastern Europe (e.g., Mazo, 1994; Seremetakis, 1991; Wilce, 2009), Africa (e.g., Anyumba, 1964; Nketia, 1975), the Middle East and Asia (e.g., Naroditskaya, 2000; Racy, 1986; Wilce, 2002), and Oceania and Australia (e.g., Feld, 1982/1990; Magowan, 2007; Moyle, 1987).
Sadness has been one of the most commonly studied affects in research on music and emotion. At least in the case of Western-enculturated listeners, both adults and children readily identify particular melodies or passages as sounding "sad" (e.g., Dolgin & Adelson, 1990; Terwogt & Grinsven, 1991). The ability of music to evoke or portray sadness or grief does not appear to be limited to Western music. Anthropologists are not easily given to claims of universality, however, in the case of music-related grief, a number of scholars have pointed to an apparent commonality. For example, writing about grief expressions and situations in non-Western cultures, ethnomusicologist Greg Urban has noted that the experiences are "transparently understandable, not in need of detailed ethnographic description." (Urban, 2000, p. 151).
For Western-enculturated listeners, sadness has a long association with the minor mode. The association of the minor third and minor triad with sadness was already described in the sixteenth century by Zarlino (1558). Experimental studies by Heinlein (1928) and Hevner (1935) show that the minor mode continues to evoke sad, dejected, or serious connotations for Western-enculturated listeners.
It is important to note that the minor mode is not solely associated with sadness. For Western-enculturated listeners, the minor mode is also associated with exoticism (especially "orientalism"; Said, 1978), as well as passion and seriousness (Hevner, 1935). When the minor mode is linked to Kraepelin's cluster of acoustic cues for sadness (low pitch, small pitch movement, quiet, slow, mumbled articulation), the resulting music has a strong tendency to exhibit a sad character. "Exceptions" to the minor↔sadness association appear to confirm the need for this cluster of features. For example, W.A. Mozart's popular "Rondo Alla Turca" can hardly be described as "sad" despite the prevalence of the minor mode. Similarly, the aria "He was Despised" from G.F. Handel's Messiah is widely regarded as very sad, despite the use of the major mode. However, the "Rondo Alla Turca" is fast-paced with relatively detached articulation; whereas "He was Despised" is slow and quiet. In short, it is difficult to identify exceptions to the minor↔sad association unless the music also violates one or more of the other acoustic features identified by Kraepelin as characteristic of sad speech prosody. Other challenges to the minor↔sad association can be found in the ethnomusicological literature. For example, scales similar to the Western harmonic minor can be found in traditional Balkan music and in various North African and Middle Eastern musics, without any accompanying association with sadness (Rice, 2004).
Most music scholars now reject the notion that the minor scale is inherently sad, and attribute its sad connotations to learned associations. An early proponent of this view was Valentine (1913/1914), who proposed that Ivan Pavlov's recently-formulated concept of the conditioned reflex might account for the sad connotations evoked by the minor mode:
The general significance of the minor key for modern European ears is not due to an effect inherent in the relation of the notes in a minor interval, but is more probably the effect of association…with the custom of setting sad songs to minor keys (Valentine, 1913/1914, p. 197-8).
In effect, Valentine proposed that the sad connotations of the minor mode originated in an early accidental pairing of sad lyrics with the minor scale. This association then provided a bootstrap for a self-sustaining cultural practice unique to Western European music-making.
This view implies that the association of the minor mode with sadness is arbitrary or random. For example, the view implies that, with a different history, it might well have been the major mode that formed a learned association with sadness whereas the minor mode formed a learned association with happiness. Without suggesting that there is anything inherent about either the major or minor modes, and without suggesting that the connotations of the minor mode are anything other than culture-bound, in the study that follows, our data will suggest that the relationship between the major and minor modes may not be arbitrary.
If the minor mode tends to be used to express or represent sadness for some listeners, then we might expect to observe an association between the minor mode and those acoustic characteristics of sad speech prosody identified by Kraepelin. That is, if the minor mode is commonly involved in the expression of sadness, we might expect that, compared with major-mode music, music in the minor mode is typically: (1) lower in overall pitch, (2) employs small pitch movements, (3) is quieter, (4) entails "mumbled" articulation (e.g., legato), and (5) exhibits a slower tempo.
The results of several correlational studies are consistent with these conjectured associations. For example, Huron (2008) calculated the average melodic interval size for nearly 10,000 Western classical instrumental themes and found that the average interval size is slightly smaller for themes written in the minor mode compared with themes written in the major mode. As small pitch movements are found in sad speech prosody, one might speculate that small melodic interval sizes might also contribute to the perception of sadness—at least for Western-enculturated listeners.
One might suppose that many factors contribute to the size of melodic intervals in music. One factor is the scale itself. A pentatonic scale, for example, might encourage larger average melodic intervals than the major scale merely because there are fewer scale tones per octave. Consider, by way of illustration, the pentatonic scale consisting of the pitch classes C, D, E, G and A. For each pitch-class pairing, we might calculate the minimum interval size in semitones (e.g., C↔D = 2, C↔E = 4, C↔G = 5, C↔A = 3, D↔E = 2, etc.). 1 If all pitch transitions were equally probable, then the average interval class for random pitch sequences in the common pentatonic mode would be 3.60 semitones. By contrast, if all pitch-class transitions were equally probable, then the average interval class for random pitch sequences in the major mode would be 3.43 semitones. Of course, in real music, not all pitch transitions are equally probable, so the actual average interval size will depend on the nature of the melodic organization.
Rather than presuming that all pitch transitions are equally likely, in this study, we employ the pitch transitions found in actual melodies. We will then explore the influence of scale structure on average interval size. Specifically, we will begin with the major scale and make systematic pitch modifications; for each modification we determine its effect on the average interval size for a sample of melodies. Our goal is to determine which scale modifications most reduce the average melodic interval size. If smaller interval sizes are robust acoustic cues for sadness, one might expect that the scale modification that results in the smallest average interval size would also tend to most contribute to the perceived sadness of a melody.
To anticipate our results, we will see that among the optimum modifications to the major scale, lowering the third and sixth scale tones—as in the harmonic minor scale—provides one of the best means for reducing the average melodic interval size. That is, the results are consistent with the idea that transposing a major-mode melody to the harmonic minor scale is among the very best pitch-related transformations that can be done to modify a major-mode melody in order to render a sad affect. Skeptics are likely to view this result as too good to be true. Accordingly, in the final Discussion, we will consider and identify the statistical properties of Western major-mode melodies that are the proximal cause of this striking result.
METHOD
In brief, our method can be best understood by describing the following hypothetical scenario. Suppose a composer has created several melodies in the major mode, and wants to transform these melodies so that they sound sadder. Research in speech prosody suggests that making the melodic intervals smaller will contribute to the perceived sadness. Rather than merely compressing all of the melodic intervals, our composer wishes to achieve a smaller average interval size by modifying the pitches of the major scale. Are there pitch modifications that can be made to the major scale that will, on average, transform most melodies so that the average melodic interval is smaller?
Our method involved assembling three contrasting samples of melodies in the major mode, calculating the average melodic interval size for each melody, and then determining whether the average interval size increases or decreases for different scale modifications. In this study, we will limit ourselves to modifications of the Western diatonic major scale. In principle, the same method could be applied to any scale from any culture—and so the potential cross-cultural generality of the hypothesis might be tested.
In modifying the pitch of a scale tone, one consideration is the amount of modification. In the case of the Western equally-tempered pitch set, the smallest modification would be a semitone. Larger modifications are possible, but they risk potential perceptual confusions. Obviously, if we were to raise the second scale degree (supertonic) by 2 semitones the resulting scale tone would be indistinguishable from the third scale degree (mediant). It is therefore unlikely that the resulting pitch would be heard as a "modified supertonic." In the major scale, any modification greater than one semitone will lead to such confusions. Moreover, even in the case of semitone modifications, there are four changes that will also lead to similar scale-degree confusions: raising the third scale tone, lowering the fourth scale tone, raising the seventh scale tone, and lowering the tonic. A further restriction is that the tonic pitch remains fixed: one might reasonably argue that changing the tonic will cause the scale to be perceived as an entirely different scale rather than as a modified version of some original. For similar reasons, we will avoid modifying more than half of the scale tones at a time. That is, we will consider only modifying up to three scale tones. We conjecture that listeners would tend to hear four or more modified pitches as an entirely different scale—rather than a modified major scale. Accordingly, we will limit ourselves to one, two or three pitch modifications of just one semitone; we will avoid modifying the tonic, and we will exclude from consideration those semitone modifications that result in pitches equivalent to other scale tones.
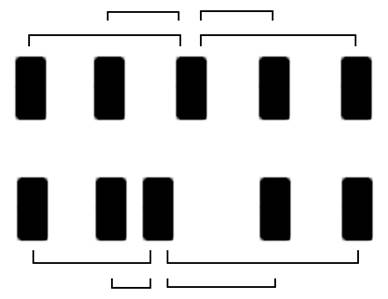
Intuitively, one might suppose that lowering one or another scale tone might tend to result in smaller melodic intervals. However, this is not necessarily the case. Lowering a scale tone might well result in larger average melodic intervals. If, in some hypothetical culture, all of the scale tones occurred with equal probability and the successions of different scale tones were randomly ordered, then modifying one of the scale tones would have no effect on the average interval size. Figure 1 illustrates this effect for a hypothetical five-note scale. In this case, the third tone has been lowered. Notice that intervals such as 1-3 and 2-3 will be smaller; however, the intervals 3-4 and 3-5 will be larger in size. In this case, it is not clear that lowering the third scale tone would have any effect whatsoever on the average interval size for melodies employing this scale.
 |
Original Scale
Modified Scale (3rd tone lowered) |
| Smaller Intervals Larger Intervals |
Fig. 1. Effect of pitch modification for a hypothetical five-note scale. Lowering the third scale tone (lower image) causes intervals such as 1-3 and 2-3 to be smaller, whereas intervals 3-4 and 3-5 are larger. If all pitches occur with equivalent frequency and all pitch transitions are equally likely, then modifying a scale tone should have no overall effect on the average interval size.
In real music, however, scale tones are not equally common, and some tone successions occur much more frequently than others. Figure 2 shows the probability of different scale-tone successions for a large sample of Germanic folk melodies in the major mode (from Huron, 2006). The width of each arrow is proportional to the probability that one tone is followed by another. Pitch transitions whose probabilities are less than 0.015 are not indicated. Notice that there is considerable variability in the likelihood of different tone successions. For example, the third and fourth scale tones are closely linked. In the case of the seventh scale tone, there is a much stronger connection to the first scale tone (7-1) than to the sixth tone (6-7). In fact, there is so little movement between 6 and 7 that the probability falls below the 0.015 threshold needed to draw a line connecting them. In the major scale, if we were to lower the seventh scale tone by one semitone, the distance between 6 and 7 would be reduced, but the distance between 7 and 1 would be increased. Since alternations between 7 and 1 are more common than between 6 and 7, the likely consequence of lowering the seventh scale tone would be to increase the average melodic interval size.
Given the fact that some scale tones are more common than others, and that some successions between scale-tones occur more frequently, modifying the pitch of a given tone might well be expected to influence the average melodic interval size for common melodies, unlike the neutral situation illustrated in Figure 1. Accordingly, we will systematically modify the different scale tones and measure the effect on the average interval size for samples of real major-mode melodies. In order to pursue this approach, we must first identify a suitable sample of melodies.
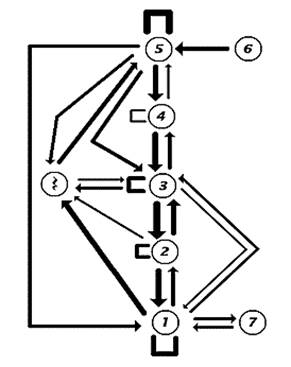
Fig. 2. The probability of different scale tone successions for a very large sample of melodies in the major mode. Frequency of occurrence is proportional to the width of connecting lines. Lines are drawn only for those transitions with a probability of 0.015 or greater (Huron 2006).
SAMPLE
Since we are interested in melodic intervals, we restricted our musical sample to single-line melodies and themes. For this study, only melodies in the major mode were used. Creating a "representative" sample of music in the major mode raises significant challenges. Instead of attempting to create a broadly representative sample, we proposed to examine three subsamples, each exhibiting a different set of stylistic properties and biases. Specifically, our three subsamples included:
1) 151 major-mode national anthems including countries such as Albania, Colombia, North Korea, Palau and Zimbabwe. Although the anthems originate from different cultures, they all share a basically Western-European musical template which includes the tendency to employ the major scale. This sample was selected from a longer list of 195 national anthems. Roughly 20 anthems were deemed to be not clearly in the major mode and so were excluded from the sample. In addition, in order to minimize the potentially confounding effect of modulation, anthems longer than 50 measures in length were excluded. According to this latter criterion another 20-odd anthems were eliminated.
2) 935 randomly selected major-mode instrumental themes from the Barlow and Morgenstern Dictionary of Musical Themes (Barlow & Morgenstern, 1948). This collection includes themes from the period-of-common-practice Western art-music literature with a bias towards orchestral works from the 19th century.
3) 103 major-mode works from a collection of songs most well-known to residents of the United States, including such songs as "Jingle Bells," "Happy Birthday," "Three Blind Mice," "Frosty the Snowman," "Yankee Doodle," "Mary Had a Little Lamb," and "Auld Lang Syne."
Although we would not claim that our sample of major-mode melodies is representative of Western music-making in general, our three samples includes both instrumental and vocal works, music of European and American origin, art-music and popular styles, music spanning a period of roughly four centuries, and instances of music from a genre that spans many countries. The sample also includes whole melodies and shorter thematic statements. It should be noted that the average passage lengths differ for the three samples. For the national anthems, the average length was 104 notes; for the American songs, the average length was 53 notes; and for the Barlow and Morgenstern instrumental themes, the average length was 20 notes. In general, effect sizes are likely to be smaller for the shorter sampled passages.
All of the musical materials were encoded in a computer database and were processed using the Humdrum Toolkit (Huron, 1995). In total, our sample represents passages from some 1,189 individual works involving roughly 40,000 notes. In carrying out our analyses, we will report separate results for each of the three samples.
PROCEDURE
For each work in the three samples, the average melodic interval size was measured only for immediately consecutive tones. No intervals were calculated for tones separated by a rest. Figure 3 illustrates the measurement method for the beginning of "Mary Had a Little Lamb." Figure 3a shows the original (unmodified) song in C major. The overall average interval size is indicated below each example. Figure 3b shows what happens when the third scale tone (E) is lowered by one semitone. Five intervals are affected, and the overall average interval size is reduced slightly.

Fig. 3. The effect of lowering the third scale tone (E) for the beginning of "Mary Had a Little Lamb."
Fig. 3a shows the original (unmodified) song in C major. The overall average interval size is indicated below each example. Fig. 3b shows what happens when the third scale tone (E) is lowered by one semitone.
In interpreting the results, readers should bear in mind the four restrictions imposed in our simulations:
(1) pitch modifications of only one semitone, (2) tonic remains unmodified, (3) modifications that result in pitches equivalent to other scale tones are avoided, (4) no more than three pitch modifications.
RESULTS
One-Pitch Manipulations
In our first simulation, we modified a single scale-tone by either raising or lowering it by one semitone. With seven scale tones there would nominally be 14 possible up/down modifications, however, with our imposed restrictions that number drops to 9. Once again, we avoided modifying the tonic, raising the 3rd or 7th scale tones, and lowering the 4th scale tone. After making the appropriate scale modification, we re-calculated the average melodic interval size for each of the 1,189 passages in our musical sample. For each sampled passage, the average interval size for the modified scale was compared with the average interval size for the original major-mode version. The modified passage can then be classified as exhibiting either a smaller average interval size, a larger average interval size, or no change in interval size. We could have amalgamated all of the melodies together and compared the means of the interval distributions for the modified and unmodified melodies. However, we a priori elected to treat each melody as a single observation in order to maximize data independence.
Table 1 identifies the effect on average interval size for each of the scale modifications according to the three different musical samples. Numerical values represent the percentage of melodies exhibiting smaller average interval size for the given scale modification—excluding those melodies for which the modification had no effect on the average interval size. For example, suppose that a given modification produced 35 melodies whose average interval size decreased, 65 melodies whose average interval size increased, and 25 melodies whose average interval size did not change. Discarding the unchanged melodies, 35% of the remaining melodies exhibited a decrease in the average melodic interval. Values around 50% suggest that the modification has little appreciable effect on interval sizes. Values larger than 50% suggest that the modification tends to cause melodies to have a smaller average interval size than the unmodified major-mode version. The right-most column (Average) provides a summary result for all three samples, where all samples are weighted equally. As can be seen in Table 1, the greatest decrease in average interval size occurs when scale degree 6 is lowered by one semitone: 68.0% of major-mode passages exhibit smaller average interval sizes when this scale modification is made. The second greatest decrease (60.3%) occurs when scale degree 3 is lowered.
| Table 1 | |||||
|---|---|---|---|---|---|
Two-Pitch Manipulations
Tables 2a-c report the results of our second simulation in which two pitches were concurrently modified. Separate tables are provided for each of the three musical samples. Note that these results need not echo the results of the one-pitch manipulations since changing two pitches at the same time causes complex interactions to occur. Once again, results are reported as the percent of melodies exhibiting a smaller average interval size for the given scale modification—excluding those melodies for which the modification had no effect on the average interval size.
Table 2d provides numerical averages for Tables 2a-c. As can be seen, the greatest effect occurs when the 3rd and 6th scale tones are concurrently lowered by one semitone: 68.0% of major-mode passages exhibit smaller average interval sizes when these scale modifications are made. The second largest effect (63.6%) occurs when the lowered 6th scale is linked with a raised 2nd scale tone. The third largest effects (60.7) occur with raised 2 and raised 5.
| Table 2a | ||||||||
|---|---|---|---|---|---|---|---|---|
| Table 2b | ||||||||
|---|---|---|---|---|---|---|---|---|
| Table 2c | ||||||||
|---|---|---|---|---|---|---|---|---|
| Table 2d | ||||||||
|---|---|---|---|---|---|---|---|---|
Tables 2a-c |
||||||||
Three-Pitch Manipulations
Tables 3a-c report the results of our third simulation in which three pitches were concurrently modified. Table 3d provides numerical averages for Tables 3a-c. Two scale modifications tie for exhibiting the greatest effect on reducing the average melodic interval size: (1) lowered 2, 3 and 6, and (2) lowered 3 and 6 with raised 5 (both at 62.9%). The second largest effect (58.9%) occurs with lowered 3, 6, and 7. The third largest effect (57.6%) occurs with lowered 6 and 7, with raised 2.
| Table 3a | ||||||||
|---|---|---|---|---|---|---|---|---|
| Table 3b | ||||||||
|---|---|---|---|---|---|---|---|---|
| Table 3c | ||||||||
|---|---|---|---|---|---|---|---|---|
| Table 3d | ||||||||
|---|---|---|---|---|---|---|---|---|
Tables 3a-c |
||||||||
DISCUSSION
Since the percentages reported in Tables 1, 2 and 3 were all calculated using the same method, we can compare the values between tables. If we ask, of all the 1-, 2- or 3-tone modifications examined in this study, which produced the greatest proportion of passages exhibiting smaller average melodic interval sizes, the answer is a tie: (1) lowering the sixth scale tone alone, and (2) lowering the third and sixth scale tones concurrently. Notice that the summary percentages for three-pitch modifications are generally lower than for one- and two-pitch modifications. That is, modifying three pitches does not appear to produce a more effective way of reducing average melodic intervals compared with either one- or two-pitch modifications.
By way of summary, for melodic passages in the major mode, those scale modifications that most reduce the average melodic interval size involve either lowering the 6th scale tone, or lowering the 3rd and 6th scale tones. Musicians will recognize the latter modification as the harmonic minor scale—the most common form of the minor mode. If (as the speech prosody research suggests) small pitch movement is associated with conveying or representing sad affect, and if a Western-enculturated musician aims to modify a major-mode melody so that it conveys or represents sadness, then it appears that lowering the third and sixth scale tones is likely to provide an optimum, or near optimum, solution.
Why?
Skeptics are likely to view the above results as too good to be true. Why, one might ask are the lowered third and sixth scale tones so effective in reducing the average melodic intervals for major-mode melodies? The answer is evident in Figure 2 which summarizes the probabilities for different scale-degree successions. The sixth scale degree has a strong affinity for the fifth scale degree. At the same time, the seventh scale degree has a strong affinity for the tonic. Lowering 6 reduces the distance between 5 and 6. Normally, this effect would be offset by the increased distance between 6 and 7, however, since there is relatively little activity between 6 and 7, the reduced melodic distance is not entirely offset by the increased distance between 6 and 7.
In the case of the third scale degree, there is more activity between 3 and 2 than there is between 4 and 3. In addition, there is more activity between 3 and 1 than between 5 and 3. Together, these asymmetries mean that lowering the third scale tone produces more smaller intervals than larger intervals. Since the asymmetry is greatest for 5-6 and 6-7, lowering 6 has a greater impact than lowering 3. In short, the results of our computationally intensive simulations may already have been inferred from the raw statistical probabilities of scale-degree transitions for major-mode melodies. Said another way, the apparent effectiveness of the harmonic minor mode in reducing melodic interval sizes can be directly attributed to the statistical properties of major-mode melodies themselves.
CONCLUSION
In this study we have sought to explain one small aspect of how sad affect may be represented or conveyed to Western-enculturated listeners. Existing perceptual research suggests that small pitch movement is associated with sad affect in speech and other auditory stimuli. By modifying one, two, and three pitches for major-mode melodies and comparing the average interval sizes to the unmodified versions, we were able to calculate which modifications could best contribute to reducing the overall melodic interval size, and so potentially contribute to the melody's ability to convey or portray sadness.
For single-note modifications, we found that lowering the sixth scale degree provided the best choice for reducing the overall average interval size. The lowered sixth was followed closely by the lowered third. The reason why these scale tones have such a marked impact on average interval size arises from common scale-degree patterns in major-mode melodies. Specifically, the proximal cause is the relative absence of melodic "traffic" between 6 and 7, along with a preponderance of melodic traffic between 6 and 5 and between 3 and 2.
Two-note modifications produce many complex interactions. Nevertheless, we found that simultaneously lowering the third and sixth scale degrees produced an optimum or near optimal effect in reducing the average melodic interval size for our sample of major-mode melodies. Of course, these modifications result in the common harmonic minor scale.
Three-note modifications produced a somewhat more complicated picture. The natural minor was not the most effective modification in lowering the average interval size. None of the three-pitch modifications proved as effective as either the one-pitch modification of lowering 6, or the two-pitch modification of lowering 6 and 3.
In general, the results replicate Huron (2008) who calculated the average melodic interval size for nearly 10,000 Western classical instrumental themes and found that the average interval size is slightly smaller for themes written in the minor mode compared with the major mode. However, the current study extends the earlier work by demonstrating that the harmonic minor mode represents an optimum or near optimum transformation for major-mode melodies if the aim is to minimize average melodic interval size.
Caveats
It is important to place the results of this study in appropriate context. First, as can be seen from Tables 1-3, there is considerable variability in the results between the three musical samples. Since the melodic passages used in our study do not necessarily constitute a representative sample of Western major-mode melodies, the generalizability of the results remains uncertain. Second, the results reported here say nothing about the relationship between the major and harmonic minor scales per se. Rather, the results depend on the structure of major-mode melodies. It is not that the minor and major scales are co-adapted for contrasting sad and non-sad expression. Instead, it is that the harmonic minor mode is well adapted to major-mode melodies for contrasting sad and non-sad expression. Third, our results say nothing about the historical relationship between the major and minor modes. For example, the results should not be viewed as suggesting that the major scale arose first, and then the harmonic minor scale grew out of this, or that the existence of the minor mode ultimately reshaped major-mode melody-writing so as to enhance the intervallic contrast. Fourth, although it is possible that the major and harmonic minor scales have some sort of "natural" origin, the results in this study cannot be interpreted as demonstrating any natural origin for either scale.
Fifth, it is important to recognize that this study has addressed only one factor known to contribute to auditory-related sadness for Western-enculturated listeners. In addition to smaller pitch movement, other factors known to contribute to sad affect include quieter dynamic level (e.g., Turner & Huron, 2008), slower tempo (e.g., Post & Huron, 2009), darker timbre and more legato articulation (e.g., Schutz, Huron, Keeton, & Loewer, 2008), and lower than normal pitch (e.g., Huron, 2008; Huron, Yim, & Chordia, 2010). Transposing a passage from major to minor mode is not, in itself, sufficient to evoke, express, or represent a sad affect (e.g., Ladinig & Huron, 2010). Nevertheless, for Western-enculturated listeners, transposition to the minor mode has a strong likelihood of making a passage sound sadder (Heinlein, 1928; Hevner, 1935).
Having shown that the harmonic minor scale is among the optimum transformations for reducing the average interval size for major-mode melodies, one might ask whether a reverse relationship is also evident. That is, suppose one assembled a sample of minor-mode melodies and posed the question: what modifications to the minor scale would most increase the average interval size for minor-mode melodies? Is the major mode an optimum scale for increasing the melodic interval size of minor-mode melodies—and so for transforming a nominally sad melody into a more joyful or happy passage? We did not pursue this reverse test because of difficulties assembling a sample of melodies that are unambiguously in the minor mode. Even short melodies (such as Greensleeves) commonly exhibit mixed major- and minor-mode passages. In addition, minor-mode melodies often employ melodic minor contours in which the 6th and 7th scale tones are treated differently in ascending and descending contexts. In principle, a future research project could establish a systematic method for handling the various distinctive properties and exceptions found in minor-mode melodies.
The phenomenon apparent in this study may or may not be limited to Western culture. In principle, the cultural generality or cultural specificity of this effect can be empirically tested (cf. Moore, 2008). If, in some non-Western culture, there exists an association where one mode is linked to "sadness" and another mode is not so linked, then the conjecture of cultural generality can be tested by measuring the effect on average interval size when musical lines in one mode are modified to conform to the other. Failing to show such an effect would suggest that the relationship identified in our study is specific to Western culture. Although the results of such a test might invite speculation, a scholarly approach would warrant actual empirical study. 2
NOTES
- Among music theorists, these minimum interval measures are referred to as interval classes (Rahn, 1980). For any pair of pitch-classes, the corresponding interval-class ignores pitch direction, collapses octave and compound (supra-octave) intervals into their sub-octave equivalents, and also treats inversions as equivalent.
Return to Text
- An earlier version of this study was published as Huron & Davis (2010).
Return to Text
REFERENCES
- Anyumba, H. Owuor (1964). The Nyatiti Lament Songs. East Africa Past and Present. Paris: Preésence africaine.
- Banse, R., & Scherer, K.R. (1996). Acoustic profiles in vocal emotion expression. Journal of Personality and Social Psychology, Vol. 70, pp. 614-636.
- Barlow, H., & Morgenstern, S. (1948). A Dictionary of Musical Themes. New York: Crown.
- Bergmann, G., Goldbeck, T., & Scherer, K.R. (1988). Emotionale Eindruckswirkung von prosodischen Sprechmerkmalen. Zeitschrift für Experimentelle und Angewandte Psychologie, Vol. 35, pp. 167-200.
- Breitenstein, C., van Lancker, D., & Daum, I. (2001). The contribution of speech rate and pitch variation to the perception of vocal emotions in a German and an American sample. Cognition & Emotion, Vol. 15, pp. 57-79.
- Davitz, J.R. (1964). Auditory correlates of vocal expressions of emotional meanings. In J.R. Davitz (Ed.), Communication of Emotional Meaning. New York: McGraw-Hill, pp. 101-112.
- Dolgin, K.G., & Adelson, E.H. (1990). Age changes in the ability to interpret affect in sung and instrumentally presented melodies. Psychology of Music, Vol. 8, pp. 87-98.
- Eldred, S.H., & Price, D.B. (1958). A linguistic evaluation of feeling states in psychotherapy. Psychiatry, Vol. 21, pp. 115-121.
- Fairbanks, G., & Pronovost, W. (1939). An experimental study of the pitch characteristics of the voice during the expression of emotion. Speech Monographs, Vol. 6, pp. 87-104.
- Feld, S. (1982/1990). Sound and Sentiment: Birds, Weeping, Poetics, and Song in Kaluli Expression (2nd ed.). Philadelphia: University of Pennsylvania Press.
- Heinlein, C.P. (1928). The affective characteristics of the major and minor modes in music. Journal of Comparative Psychology, Vol. 8, pp. 101-142.
- Hevner, K. (1935). The affective character of the major and minor mode in music. American Journal of Psychology, Vol. 47, pp. 103-118.
- Huron, D. (1995). The Humdrum Toolkit: Reference Manual. Menlo Park, California: Center for Computer Assisted Research in the Humanities.
- Huron, D. (2006). Sweet Anticipation: Music and the Psychology of Expectation. Cambridge, Massachusetts: MIT Press.
- Huron, D. (2008). A comparison of average pitch height and interval size in major- and minor-key themes: Evidence consistent with affect-related pitch prosody. Empirical Musicology Review, Vol. 3, pp. 59-63.
- Huron, D., & Davis, M.J. (2010). The effect of scale degree modifications on average interval size. In S.M. Demorest, S.J. Morrison, & P.S. Campbell (Eds.), Proceedings of the 11th International Conference on Music Perception and Cognition. Seattle, Washington: Causal Productions, pp. 439-444.
- Huron, D., Yim, G., & Chordia, P. (2010). The effect of pitch exposure on sadness judgments: An association between sadness and lower than normal pitch. In S.M. Demorest, S.J. Morrison, & P.S. Campbell (eds.), Proceedings of the 11th International Conference on Music Perception and Cognition. Seattle, Washington: Causal Productions, pp. 63-66.
- Huttar, G. (1968). Relations between prosodic variables and emotions in normal American English utterances. Journal of Speech and Hearing Research, Vol. 11, pp. 467-480.
- Kraepelin, E. (1899/1921). Psychiatrie. Ein Lehrbuch für Studierende und Ärzte, ed. 2. Klinische Psychiatrie. II. Leipzig: Johann Ambrosius Barth, 1899. Trans. By R. M. Barclay as Manic-Depressive Insanity and Paranoia. Edinburgh: E. & S. Livingstone. 1921.
- Ladinig, O., & Huron, D. (2010). Dynamic levels in Classical and Romantic keyboard music: Effect of musical mode. Empirical Musicology Review, Vol. 5, pp. 27-35.
- Magowan, F. (2007). Melodies of Mourning: Music and Emotion in Northern Australia. Crawley, Australia: University of Western Australia Press.
- Mazo, M. (1994). Lament made visible: A study of paramusical elements in Russian lament. In: B. Yung & J.S.C. Lam (Eds.), Themes and Variations: Writings on Music in Honor of Rulan Chao Pian. Hong Kong: Harvard Department of Music and the Center for Chinese Studies, The Chinese University of Hong Kong, pp. 164-211.
- Moore, S. (2008). The Doom of the Flattened Supertonic: The 'other leading note' in Turkish makam, Indian raga, klezmer and heavy metal musics. MA Thesis in World Music Studies, Department of Music, University of Sheffield.
- Moyle, R. (1987). Tongan Music. Auckland, NZ: Auckland University Press.
- Naroditskaya, I. (2000). Azerbaijanian female musicians: Women's voices defying and defining the culture. Ethnomusicology, Vol. 44, pp. 234-256.
- Nketia, J.H.K. (1975). The Music of Africa. London: Gollancz.
- Post, O., & Huron, D. (2009). Music in minor modes is slower (Except in the Romantic Period). Empirical Musicology Review, Vol. 4, pp. 1-9.
- Racy, A.J. (1986) Lebanese laments: Grief, music, and cultural values. The World of Music, Vol. 28, pp. 27-40.
- Rahn, J. (1980). Basic Atonal Theory. Prentice-Hall.
- Rice, T. (2004). Music in Bulgaria: Experiencing Music, Expressing Culture. Oxford: Oxford University Press.
- Said, E.W. (1978). Orientalism. New York: Vintage.
- Schutz, M., Huron, D., Keeton, K., & Loewer, G. (2008). The happy xylophone: Acoustic affordances restrict an emotional palate. Empirical Musicology Review, Vol. 3, pp. 126-135.
- Seremetakis, C.N. (1991). The Last Word: Women, Death, and Divination in Inner Mani. Chicago: University of Chicago Press.
- Skinner, E.R. (1935) A calibrated recording and analysis of the pitch, force and quality of vocal tones expressing happiness and sadness. Speech Monographs, Vol. 2, pp. 81-137.
- Sobin, C., & Alpert, M. (1999). Emotion in speech: The attributes of fear, anger, sadness, and joy. Journal of Psycholinguistic Research, Vol. 28, pp. 347-365.
- Terwogt, M.M., & Van Grinsven, F. (1991). Musical expression of moodstates. Psychology of Music, Vol. 19, pp. 99-109.
- Turner, B. & Huron, D. (2008). A comparison of dynamics in major- and minor-key works. Empirical Musicology Review, Vol. 3, pp. 64-68.
- Urban, G. (2000). A Discourse-Centered Approach to Culture: Native South American Myths and Rituals. Tucson, Arizona: Hats Off Books, 2nd edition.
- Valentine, C.W. (1913/1914). The aesthetic appreciation of musical intervals among school children and adults. British Journal of Psychiatry, Vol. 6, pp. 190-216.
- Wilce, J.M. (2002). Genres of memory and the memory of genres: Forgetting lament in Bangladesh. Comparative Studies in Society and History, Vol. 44, pp. 159-185.
- Wilce, J.M. (2009). Crying Shame: Metaculture, Modernity, and the Exaggerated Death of Lament. Chichester, UK: Wiley-Blackwell.
- Williams, C.E., & Stevens, K.N. (1972). Emotions and speech: Some acoustic correlates. Journal of the Acoustical Society of America, Vol. 52, pp. 1238-1250.
- Zarlino, G. (1558). Le istitutioni harmoniche.
APPENDIX
National Anthems Used
Afghanistan, Albania, Andorra, Angola, Antigua and Barbados, Armenia, Australia, Austria, Bahamas, Barbados, Belarus, Belgium, Belize, Benin, Bhutan, Bosnia and Herzegovina, Botswana, Brunei, Burkina Faso, Cambodia, Cameroon, Canada, Cape Verde, Chad, China, Colombia, Comoros, Congo, Congolaise, Costa Rica, Croatia, Cuba, Cyprus, Czech Republic, Denmark, Djibouti, Dominica, Dominican Republic, Egypt, Equatorial Guinea, Eritrea, Estonia, Fiji, Finland, France, Gambia, Germany, Ghana, Gibraltar, Greece, Grenada, Guatemala, Guinea, Guinea Bissau, Guyana, Haiti, Hungary, Iceland, Indonesia, Iran, Iraq, Ireland, Isle of Man, Ivory Coast, Jamaica, Jordan, Kazakhstan, Kiribati, North Korea, South Korea, Kyrgyzstan, Laos, Latvia, Lebanon, Lesotho, Liberia, Libya, Liechtenstein, Lithuania, Luxembourg, Macedonia, Madagascar, Malawi, Malaysia, Maldives, Mali, Malta, Marshall Islands, Mauritius, Mexico, Micronesia, Moldova, Monaco, Mongolia, Mozambique, Myanmar, Namibia, Nauru, Nepal, Netherlands, New Zealand, Nicaragua, Nigeria, Norway, Oman, Palau, Papua New Guinea, Poland, Portugal, Principe, Russia, Rwanda, Saint Lucia, San Marino, Saudi Arabia, Senegal, Serbia and Montenegro, Seychelles, Sierra Leone, Singapore, Slovenia, Solomon Islands, Somalia, Sri Lanka, St. Kitts and Nevis, St. Vincent and Grenadines, Sudan, Surinam, Swaziland, Sweden, Switzerland, Syria, Taiwan, Tajikistan, Tanzania, Thailand, Togo, Tonga, Tunisia, Tuvalu, USA, Uganda, United Arab Emirates, United Kingdom, Uzbekistan, Vanuatu, Vietnam, Wales, Yemen, Zambia, and Zimbabwe.
AUTHOR NOTE:
Correspondence concerning this article should be addressed to:
David Huron, School of Music, 1866 College Road, Ohio State University, Columbus, Ohio, 43210, USA, huron.1@osu.edu

