COUNTERPOINT is a musical term that refers to the interaction of two or more musical lines that have independent rhythmic and melodic contour properties while being strictly interconnected harmonically. This is a compositional style that reached peak popularity during the Baroque period. Contrapuntal techniques are among the most strictly defined in music and often imply voice imitation, as exemplified by canons, fugues, etc., and the computational modeling of contrapuntal polyphony is an endeavor that has attracted consistent interest and effort over the years. A multiplicity of methods and strategies have been employed to this end, from rule-based systems (Ebcioglu, 1993) and statistical sampling (Allan & Williams, 2004) to more recent neural network approaches (Hadjeres, Pachet & Nielsen, 2017). For those based on machine learning, data quality is, clearly, of uttermost importance. We posit that current trends in deep learning applications to music generation (requiring vast amounts of data) might encourage blind and/or non-critical usage of readily available datasets, which, in turn, might affect the musical results obtained. As computational musicology and machine learning become increasingly coupled, it is crucial to adopt a critical position towards the usage of large datasets and to adapt, modify, and curate the vast amounts of musical data to fit the context-specific analytic or generative task one undertakes (Huron, 2013). MCMA is our contribution to the subject.
MOTIVATION
Computational musicology is well-equipped to study music empirically with tools such as the Humdrum toolkit 1, the VIS Framework (Antila & Cumming, 2014), and music21 (Cuthbert & Ariza, 2010). The latter is conveniently bundled with its own corpora, and there are also several other high-quality symbolic music corpora specifically curated with musicological analysis in mind, which are available online (Sapp, 2005; Devaney et al., 2015; Neuwirth et al., 2018; Gotham et al., 2018). However, even when combined, the available corpora only cover a very small part of the published musical works. A common strategy to increase the data size is to include MIDI-encoded performances although, for musicological analysis, the MIDI format is less congenial because it lacks pitch spelling disambiguation (e.g., a G# and an Ab are considered the same note). Moreover, MIDI keyboard input has proven to be an error-prone method. A study of a random sample of such scores from classicalarchives.com found that 8% of the encoded pitches did not match with the published score (Shanahan & Albrecht, 2013). In particular, voice separation in contrapuntal music seems to be a marginal concern when compiling a new dataset. It is true that there are available sets of string quartets and choral music that are written with independent parts 5. But most available scores of keyboard music, for example, collapse the notes of a polyphonic passage into a single staff, making the discernment of voices a difficult task, unless one has formal musical analysis skills. Empirically analyzing counterpoint music is nearly impossible without voice separation (e.g., by means of "exploding" a part into its constituent voices). To address these issues, we sourced and edited MCMA 2, a symbolic music corpus of contrapuntal works encoded with independent voices.
Using MCMA, each voice is assigned to a different track and can therefore be analyzed separately, which is convenient for investigating voice leading in counterpoint. A musicologist would be able to quickly find examples of retrograde inversions or augmentations in contrapuntal melodic lines, or find statistically valid answers for their questions: for example, what is the most common interval to use for parallel contrapuntal motion? Is contrary motion preferred to other types of motion? These questions pertain to a long-established line of computational musicological inquiry (Huron, 2016). Separating musical voices can also be valuable in an educational context. At the moment, counterpoint studies often focus on vocal parts; perhaps access to instrumental scores where voices are separated could allow students to more directly identify contrapuntal techniques. Additionally, instrumental scores typically comprise a wider array of intervallic motion and duration/subdivisions than does vocal repertoire (which results from the physical limitations of the human voice). Figure 1 shows a trivial example. This affordance could then be further enhanced if coupled with the usage of score annotation software, for example, Dezrann (Giraud et al., 2018).

Fig. 1. Comparing the first three bars of J.S. Bach's Fugue No.3 in C# Major BWV 872, from the Well-Tempered Clavier, Book II, (top) against the same extract in MCMA's corpus (bottom).

Fig. 2. The first two bars of J.S. Bach's first two-part inventions viewed as a "query-answer" problem.
We also envisage uses of MCMA in the domain of generative models. For example, the relation between two voices in a contrapuntal piece becomes paramount if one wants to employ natural language processing models and treats one voice as the musical response to a "query." As an example of MCMA's application, Nichols et al. (Forthcoming, 2021) consider the task of neural machine translation (e.g., English to Japanese) where the "source sentence" is one musical voice and the "target sentence" is another simultaneous contrapuntal voice. Figure 2 illustrates this task. As in translation, the source imposes some constraints on the target, but it doesn't define it completely. Unlike in translation, contrapuntal musical interactions are nearly synchronous, and both source and target have the same vocabulary. Despite these caveats, it is possible to envisage practical applications using this paradigm.
These are but few possible applications of MCMA, and we look forward to seeing many more appropriations of this corpus.
THE MCMA CORPUS
MCMA aims at being Findable, Accessible, Interoperable, and Reusable, in adherence to the FAIR principles 3. It has an extensive metadata protocol, which is described in detail in its documentation 2. The metadata is registered in comma-separated value files, one per collection: each musical work is assigned a globally unique and persistent identifier and is richly described with a plurality of accurate and relevant attributes. We sourced the pieces in MCMA from disparate readily available online datasets/databases under free-content licensing. For most of the files presented in MCMA, we started our curation process from symbolic scores already available in the Werner Icking Archive 4, KernScores 5, MuseScore 6, and other online sources 7-9. Regardless of the provenance's encoding format, we then proceeded to convert every piece in MCMA to compressed musicXML (mxl), which supports correct pitch spelling (a sine qua non for musicological analysis) and is natively supported by most visual editors, potentially catering for a less techno-affluent demographic. This required a careful comparison of the resulting files with the published edition of the scores available on the International Music Score Library Project (IMSLP) 10 to remove all errors (pitch spelling, spelled out ornaments, corrupted files, etc.). Roughly two thirds of the material presented required extensive modification in this stage. The last step was the separation of each piece into tracks. Arguably, MCMA's most important contribution is the multi-track expansion of several of J.S. Bach's harpsichord works (e.g., The Goldberg Variations, the complete Well-Tempered Clavier, the Art of the Fugue, and the Sinfonias). Considering WTC, although a track-separated version was already available in KernScores, we created/edited an independent version 11.
Furthermore, MCMA's versions also remove, when present, expression markings, dynamics and embellishments which were supposedly introduced via MIDI performance (but which were not present in the original score).
In the context of this work, a "track" is a technical term we use to refer to a single predominantly monophonic voice from a polyphonic piece encoded as a part of musicXML score. In MCMA, the occasional polyphony within a track is kept. For example, if a fugue is considered to be in 4 voices, the corresponding MCMA file will contain exactly 4 tracks, some of them having multiple voices for a short time (this "sporadic polyphonic split," in which a single track temporarily becomes polyphonic, is akin to **kern's spine split) (Huron, 1997). The specific choices pertaining to this splitting are not functionally crucial, but have important implications in terms of musical perception, aesthetics, and stylistic authenticity. Therefore, resolving sporadic polyphonic splits requires careful consideration to avoid having to add an extra, mostly empty, part.

Fig. 3. Comparing bar 32 of J.S. Bach's Fugue No.3 in C# Major BWV 872, from the Well-Tempered Clavier, Book II, (top) against the same extract in MCMA's corpus (bottom).
There are good reasons why one would want to avoid this. For example, to maintain the polyphonic coherence and the number of voices intended (and/or specified) by the composer. This also ensures that each track is musically more meaningful and functional. Figure 3 shows an example taken from the same fugue in Figure 1. This particular fugue is in three voices; therefore, it was expanded to three tracks. However, in bar 32 through to the end (bar 35) the polyphonic texture becomes denser. This passage is, in MCMA, dealt with simply by means of splitting track 2 into dyads (same voice), while keeping the added voice in track 3. While we are aware that these choices might be arguable in some cases, we consider this a necessary step towards the creation of a multi-track collection of contrapuntal pieces and argue that, given the sparsity of their occurrence and the overall keeping of all the original notes, the specifics of which track notes are reassigned to are of lesser importance.
The occasional polyphony within individual tracks which often occurs in near correspondence of terminal cadenzas is generally not as problematic, and easily dealt with. Figure 4 exemplifies this case.

Fig. 4. The last bar of J.S. Bach's Prelude No.6 in D minor BWV 851, from the Well-Tempered Clavier, Book I, multi-track expanded in MCMA's corpus.
The choices behind the processing/editing process described thus far are informed by musicological concerns, whereby we aim at preserving the original pieces' harmonic and melodic integrity, particularly with respect to voice-leading.
At the time of writing, MCMA comprises 475 files. Each file is either a piece in its entirety or a section from a larger piece. Examples of the latter are sonata movements, single variations in a set of theme and variations, or, in the case of an opera, sections of a scene. The music represented in MCMA is by 5 Baroque composers and written between 1674 and 1750. Its combined duration is 76,699 quarter notes, which amounts to approximately 12 hours if one assumes an average bpm (beats per minute) of 108 (see Table 1).
| Composer | Number of Pieces | Publication Years | Total duration (quarter note, hours) |
|---|---|---|---|
| Albinoni, Tomaso | 72 | 1708 – 1712 | 9,406.75 ♩ ≈ 1h30' |
| Bach, Johann Sebastian | 178 | 1722 – 1750 | 33,171.25 ♩ ≈ 5h10' |
| Becker, Dietrich | 45 | 1674 | 7,505.00 ♩ ≈ 1h10' |
| Buxtehude, Dietrich | 88 | 1694 – 1696 | 11,019.00 ♩ ≈ 1h40' |
| Lully, Jean-Baptiste | 92 | 1682 | 15,597.00 ♩ ≈ 2h20' |
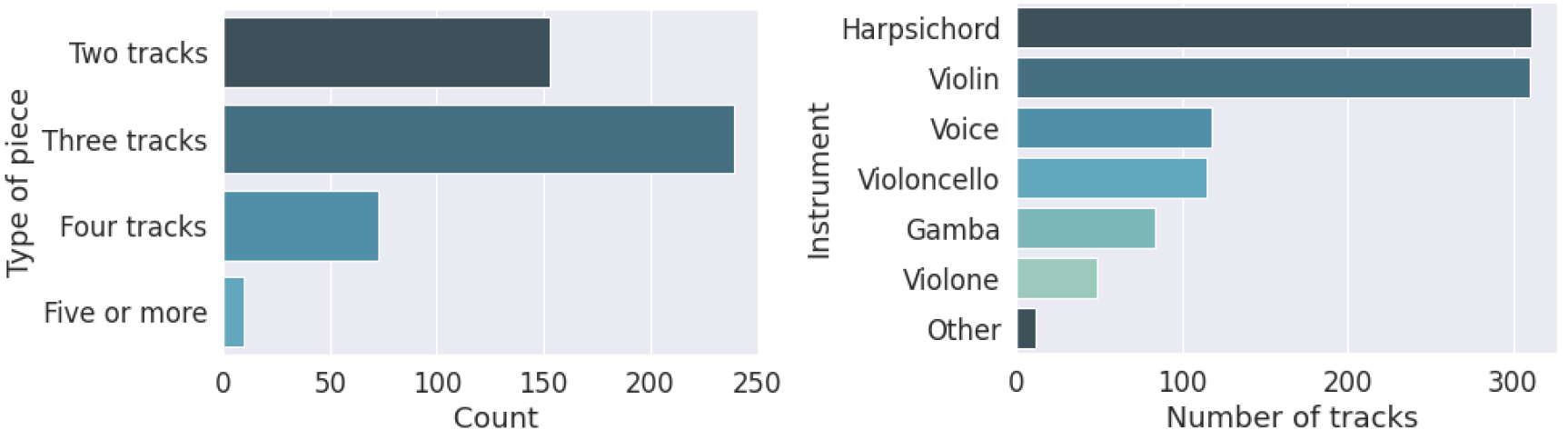
Each file contains between two and six tracks at most, with the majority (239) being in three tracks, 153 in two tracks, and 83 in four or more tracks (see Figure 5, left). There are tracks played by nine different instruments: 31% of harpsichord and 31% of violin, and the remaining divided between violoncello, voice, gamba, violone, tenor viol, oboe, and bassoon (see Figure 5, right).
CONTRIBUTIONS & FUTURE WORK
MCMA's core archive is rather small at the time of writing. Rather than aiming to release a completed corpus with sporadic version updates, we decided to extend a call for contributions to the wider community. We anticipate this to be an endeavor of interest for the music information community and for musicologists, in general. In the project's documentation 2, detailed instructions for contributors are outlined, and the functionality of the utility assets is explained. The latter include Python scripts for the automatic generation of the metadata for a given musical collection (contingent upon the invariance of some of the metadata fields, such as the provenance, the reference edition, etc.), the statistical analysis of the corpus, and metadata templates. If the contribution challenge were to attract sufficient interest from the community, MCMA's size could grow considerably, making it even more apt for machine learning applications (large data is a deciding factor in this context).
Besides the addition of more contrapuntal pieces, future work includes extending MCMA via a tagged query-response subset (akin to SQuAD 12) which will entail meticulous musicological effort in identifying variable-length musical phrases that correspond to each other. While this process can be partly automated via segmentation algorithms (Tenney & Polansky, 1980; Cambouropoulos, 2001) and strategies such as Dynamic Time Warping (Gold & Sharir, 2018), it still requires human intervention and editing.
We also plan to build an interactive companion website to MCMA, whereby users who are not necessarily techno-affluent can sort, organize and explore the corpus's content. Such an interactive version of MCMA might include in-browser score rendition and database functionality (e.g., aggregate functions) which can be used as a first port of call for basic statistical enquiry of the musical archive. Additionally, more sophisticated and domain-specific functionality regarding automatic feature extraction could be added to said companion website, to include visualization of melodic contours, distributions (e.g., pitch and interval class, etc.), n-gram analysis, Implication-Realization Model analysis (Yazawa et al., 2016), and melodic segmentation.
ACKNOWLEDGMENTS
This article was copyedited by Jessica Pinkham and layout edited by Diana Kayser.
NOTES
-
https://www.humdrum.org/
Return to Text -
https://mcma.readthedocs.io/en/latest/contents.html
Return to Text -
https://www.go-fair.org/fair-principles/
Return to Text -
http://www.icking-music-archive.org/index.php
Return to Text -
http://kern.ccarh.org/
Return to Text -
https://musescore.org/ — note that scores from this website are no longer available as MuseScore was recently acquired by the company Ultimate Guitar.
Return to Text -
http://www.jsbach.net/midi/index.html
Return to Text -
https://www.lysator.liu.se/~tuben/scores/
Return to Text -
https://www.welltemperedclavier.org
Return to Text -
https://imslp.org/
Return to Text -
As a starting point, we used the Open Well-Tempered Clavier project 9 for Book I and the work by Musescore user classicman 6 for Book II. Several independent editions were consulted in the preparation of the track-separated scores including the following: G. Henle Verlag, Urtext: Das Wohltemperiertre Klavier Teil I (2007), Willard A. Palmer: The Well-Tempered Clavier (1996), Dover: The Well-Tempered Clavier, Books I and II, Complete (1983), Dover: The Well-Tempered Clavier: 48 Preludes and Fugues, Book 1. Commentaries by Donald Francis Tovey (2014), Edition Peters, Urtext: Wohltemperiertes Klavier I, and Edition Peters, Urtext: Wohltemperiertes Klavier II.
Return to Text -
https://rajpurkar.github.io/SQuAD-explorer/
Return to Text
REFERENCES
- Allan, M., & Williams, C. K. I. (2004). Harmonising chorales by probabilistic inference. In Proceedings of the 17th International Conference on Neural Information Processing Systems. MIT Press, Cambridge, MA, 25–32.
- Antila, C., & Cumming, J. (2014). The VIS framework: Analyzing counterpoint in large datasets. In Proceedings of the 15th International Society for Music Information Retrieval Conference. Taipei, Taiwan.
- Cambouropoulos, E. (2001). The Local Boundary Detection Model (LBDM) and its application in the study of expressive timing. In Proceedings of the International Computer Music Conference. Havana, Cuba.
- Cuthbert, M. S., & Ariza, C. (2010). music21: A toolkit for computer-aided musicology and symbolic music data. In Proceedings of the 11th International Society for Music Information Retrieval Conference, Utrecht, Netherlands, 637–642.
- Devaney, J., Arthur, C., Condit-Schultz, N., & Nisula, K. (2015). Theme and Variation Encodings with Roman Numerals (TAVERN): A new data set for symbolic music analysis. In Proceedings of the 16th International Society for Music Information Retrieval Conference, 728–734.
- Ebcioglu, K. (1993). An expert system for harmonizing four-part chorales. Machine Models of Music. MIT Press, Cambridge, MA, 385–401.
- Giraud, M., Groult, R., & Leguy, E. (2018). Dezrann, a web framework to share music analysis. In International Conference on Technologies for Music Notation and Representation, 104–110.
- Gold, O., & Sharir, M. (2018). Dynamic time warping and geometric edit distance: Breaking the quadratic barrier. ACM Trans. Algorithms, 14(4), 1–17. https://doi.org/10.1145/3230734
- Gotham, M., Jonas, P., Bower, B., Bosworth, W., Rootham, D., & VanHandel, L. (2018). Scores of scores: An OpenScore project to encode and share sheet music. In Proceedings of the 5th International Conference on Digital Libraries for Musicology, 87–95. ACM, New York, NY. https://doi.org/10.1145/3273024.3273026
- Hadjeres, G., Pachet, F. & Nielsen, F. (2017). DeepBach: A steerable model for Bach chorales generation. In Proceedings of the 34th International Conference on Machine Learning, 1362–1371.
- Huron, D. (1997). Humdrum and Kern: Selective feature encoding. In Selfridge-Field, E. (Ed), Beyond MIDI: The Handbook of Musical Codes, MIT Press, Cambridge, MA, 375–401.
- Huron, D. (2013). On the virtuous and the vexatious in an age of big data. Music Perception, 31(1), 4–9. https://doi.org/10.1525/mp.2013.31.1.4
- Huron, D. (2016). Voice leading: The science behind a musical art. MIT Press, Cambridge, MA. https://doi.org/10.7551/mitpress/9780262034852.001.0001
- Neuwirth, M., Harasim, D., Moss, F. C., and Rohrmeier, M. (2018). The annotated Beethoven corpus (ABC): A dataset of harmonic analyses of all Beethoven string quartets. Frontiers in Digital Humanities, 5:16. https://doi.org/10.3389/fdigh.2018.00016
- Nichols, E.P., Kalonaris, S., Micchi, G., and Aljanaki, A. (2021). Modeling Baroque two-part counterpoint with neural machine translation. In Proceedings of the International Computer Music Conference (ICMC). Preprint available at: https://arxiv.org/abs/2006.14221
- Sapp, C.S. (2005). Online database of scores in the humdrum format. In Proceedings of the 6th International Society for Music Information Retrieval Conference, 664–665.
- Shanahan, D. & Albrecht, J. (2013). The acquisition and validation of large web-based corpora. In Proceedings of the biennial meeting of the Society for Music Perception and Cognition, 36. Toronto, Canada. https://www.musicperception.org/pastprograms/SMPC-2013.pdf
- Tenney, J., & Polansky, L. (1980). Temporal gestalt perception in music. Journal of Music Theory, 24(2), 205–241. https://doi.org/10.2307/843503
- Yazawa, S., Hamanaka, M., & Utsuro, T. (2016). Subjective melodic similarity based on extended implication-realization model. International Journal of Affective Engineering, 15(3), 249–257. https://doi.org/10.5057/ijae.IJAE-D-15-00050