DEVELOPMENT sections in sonata form are characterized by various types of instability. They tend to be harmonically adventurous, passing rapidly through multiple non-tonic keys. They often feature frenzied rhythmic activity, whirling sequences, and sudden textural shifts. And they typically involve melodic fragments, instead of tight-knit themes. As William Caplin (1998, p. 139) puts it, "A development generates the greatest degree of tonal and phrase-structural instability in the movement and thus motivates a restoration of stability (to be accomplished by the recapitulation)" (see also Hepokoski & Darcy, 2006, p. 18). This understanding of the development is central to the three-part model of sonata form that emerged in the nineteenth century. Whereas earlier theorists such as Anton Reicha understood the sonata as a large binary form, Adolf Bernhard Marx conceived of the development as an independent second part (Wood Uribe, 2011, p. 247). In Marx's view, the exposition–development–recapitulation structure corresponds to a large-scale pattern of rest–motion–rest (Burnham, 1989, p. 259). From its origins, then, the idea of a sonata-form development is premised on instability.
How might hypermeter fit into this formal paradigm? Hypermeter is a kind of high-level metrical patterning (Cone, 1968; Rothstein, 1989). It gathers measures into hypermeasures, according to a pattern of strong and weak downbeats, just as meter gathers strong and weak beats into measures. Because both hypermeter and meter coordinate cycles at multiple temporal levels, there is arguably no fundamental difference between them (London, 2012, pp. 17–18). Nonetheless, hypermeter often behaves differently from lower metrical levels, and it may be construed as a distinct syntactic layer (see Zbikowski, 2017). For example, hypermeter tends to be more flexible than meter. As David Temperley (2008, p. 305) observes, this irregularity can be formally productive: "Hypermetrical shifts can often help to emphasize the formal division between one section and another. Or a section might contain numerous hypermetrical shifts, imparting a sense of heightened tension to the entire passage. In these ways, hypermeter can play an important role in articulating the form of a piece, and in conveying a trajectory of tension and stability." Given established concepts of sonata form, development sections might be expected to have greater hypermetrical irregularity—more hypermetrical shifts, hypermetrical ambiguity, or hypermetrical dissonance.
By contrast, we hypothesize that developments have less hypermetrical irregularity than expositions or recapitulations. Expositions and recapitulations often include hypermetrical variation, with beginning-accented primary and secondary themes, and end-accented closing themes (Ng, 2012; Temperley, 2003). Moreover, repetition of multi-measure units is required for sequences, which are central to what Caplin (1998, p. 141), following Erwin Ratz, calls "the core of the development." We suggest that hypermeter in sonata developments might counterbalance other syntactic layers. In other words, hypermetrical regularity in development sections would foster a sense of "temporal orientation" (see Ito, 2013). It would provide a relatively consistent framework in which unstable events occur.
This corpus study assesses hypermetrical irregularity in expositions and developments from symphonic sonata-form movements. It also compares several eighteenth- and nineteenth-century composers—from Joseph Haydn to Antonin Dvořák—who might use hypermeter in distinct ways, according to individual preferences or historical trends.
METHOD
Sample
Our corpus comprises expositions (excluding introductions) and developments from 60 symphonic sonata-form movements. Works in the corpus were composed between 1761 and 1893, by Joseph Haydn, Wolfgang Amadeus Mozart, Ludwig van Beethoven, Franz Schubert, Felix Mendelssohn, Robert Schumann, Johannes Brahms, and Antonin Dvořák. With Haydn and Mozart, we examined a quasi-random sample of 10 symphonies from throughout their careers; for later composers, we covered their complete symphonic output.
Procedure
For each section in the corpus, two independent raters recorded measure numbers for hypermetrical downbeats. Quadruple hypermeter was taken as a default, and these analyses were informed by preference rules from the scholarly literature:
- Harmonic rhythm: "Strong beats of the meter should, where possible, coincide with changes of harmony." (Rothstein, 1995, p. 173)
- Congruence: A melody's rhythmic grouping should, where possible, correspond to its metrical organization, so a melodic phrase is generally a hypermeasure (Rothstein, 1995, p. 173).
- Parallelism: "Prefer to assign parallel metrical structures to parallel segments. In cases where a pattern is immediately repeated, prefer to place the stronger beat on the first instance of the pattern rather than the second." (Temperley, 2001, p. 51)
- Texture: "In cases where the melody begins before the accompaniment, the beginning of the accompaniment should, where possible, be metrically stronger than the beginning of the melody." (McKee, 2004, p. 5)
In ambiguous or transitional passages (such as those discussed in Bakulina, 2017; Kamien 1993; Temperley 2008), we preferred "conservative" interpretations, which maintain the prevailing hypermeter for as long as possible (see Imbrie, 1973).
Using hypermetrical downbeat locations, we derived the duration of each hypermeasure and calculated hypermetrical irregularity in two ways. First, we located hypermetrical shifts, defined for present purposes as instances where a hypermeasure is longer or shorter than the preceding group. Such shifts are often fleeting and do not necessarily establish a new kind of hypermeter. This method makes no assumptions about instituted hypermetrical norms. Second, we identified hypermetrical deviations—that is, groups that depart from the default four-measure pattern. This method recognizes that extended passages of triple hypermeter are rare, despite prominent examples such as the Scherzo from Beethoven's Ninth Symphony (see Cohn, 1992a). These approaches typically produce different values, and it seems unclear a priori how strongly they will correlate. For example, a single three-measure group in a passage of quadruple hypermeter counts as two shifts and one deviation, whereas four consecutive three-measure groups would count as two shifts and four deviations. Finally, we converted the counts for hypermetrical shifts and deviations into proportions, dividing by the total number of hypermeasures in the relevant section. Our values for hypermetrical irregularity, then, always range from 0 (maximal regularity) to 1 (maximal irregularity).
RESULTS
We set an α level of 0.05 to assess significance. Data analysis was conducted using R, v. 3.3.3 (R Core Team, 2017). Analyses by our independent raters were substantially and significantly correlated for both hypermetrical shifts (r(118) = .82, p < .001) and hypermetrical deviations (r(118) = .76, p < .001). Independent ratings for each section were averaged to produce combined ratings. Combined ratings for hypermetrical shifts were highly correlated with those for hypermetrical deviations (r(118) = .93, p < .001). However, combined ratings for hypermetrical shifts were normally distributed (W = .98, p = .1702), whereas those for hypermetrical deviations were not (W = .97, p = .01215). Because of this correlation and difference in distribution, subsequent analysis focused on hypermetrical shifts.
On average, the proportion of hypermetrical shifts was higher in expositions (M = .39, SD = .15) than in developments (M = .30, SD = .19) (see Figure 1). This difference was observed in 46 of 60 pieces (76%). The proportion of hypermetrical deviations was also higher in expositions (M = .26, SD = .13) than in developments (M = .20, SD = .13) (see Figure 1). Hypermetrical shifts were analyzed via a mixed-design analysis of variance (ANOVA), with formal section (exposition or development) as the within-piece variable and composer as the between-piece variable. Expositions had a significantly higher proportion of hypermetrical shifts than development sections (F(1,51) = 14.22, p < .001). Composers used different amounts of hypermetrical regularity (see Table 1), and there was also a highly significant main effect for composer (F(7,51) = 6.56, p < .001). The interaction between section and composer was not significant (F(7,51) = 0.80, p = .58946). There was a very weak correlation between proportion of hypermetrical shifts and year of composition, r(118) = -.19, p = .040843 (see Figure 2).
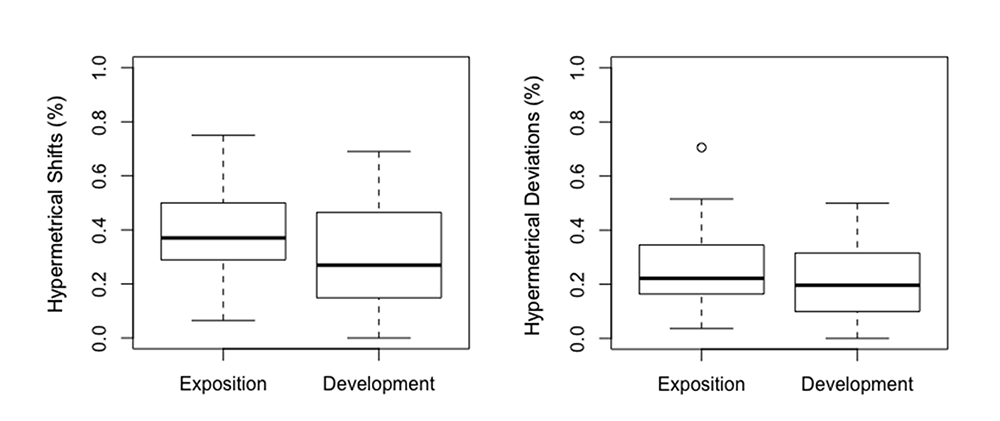
Fig. 1. Average proportion of hypermetrical shifts and hypermetrical deviants are higher in expositions, relative to developments.
| Composer | Exposition | Development | Overall | |||
|---|---|---|---|---|---|---|
| M | SD | M | SD | M | SD | |
| Haydn | .525 | .151 | .498 | .105 | .512 | .093 |
| Mozart | .429 | .149 | .317 | .155 | .373 | .106 |
| Beethoven | .330 | .099 | .134 | .127 | .232 | .074 |
| Schubert | .330 | .155 | .214 | .194 | .272 | .090 |
| Mendelssohn | .365 | .082 | .198 | .068 | .281 | .064 |
| Schumann | .246 | .115 | .210 | .102 | .228 | .091 |
| Brahms | .383 | .134 | .365 | .227 | .374 | .169 |
| Dvořák | .394 | .193 | .323 | .206 | .359 | .178 |
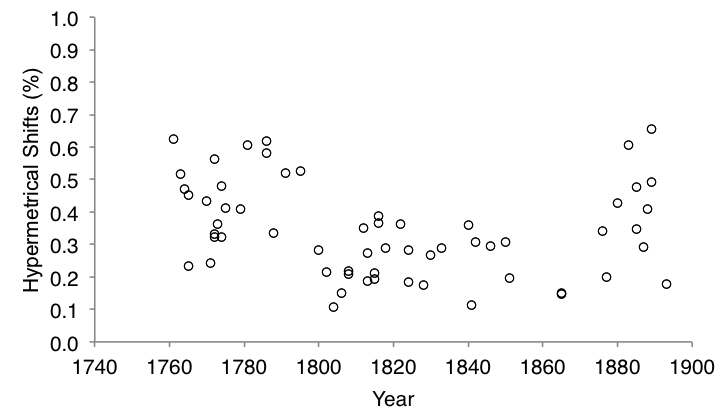
Fig. 2. Proportion of hypermetrical shifts for each movement in the corpus, ordered by year of composition
DISCUSSION
According to this corpus analysis, developments typically involve less hypermetrical irregularity than expositions. That contrast appeared in overall averages but also in 76% of the pieces in the corpus. For every composer, pieces that followed the trend were more common than those that did not. (This was especially pronounced with Beethoven and Mendelssohn, where we observed no exceptions.) And for every composer, hypermetrical irregularity, averaged across pieces, was lower in development sections.
Nonetheless, these composers used different amounts of hypermetrical irregularity. For example, Haydn's music had the most hypermetrical irregularity in the corpus—more than twice as much as Schumann's music. Table 1 and Figure 2 might suggest a historical progression with hypermetrical irregularity gradually decreasing, then increasing later in the nineteenth century. However, it is difficult to distinguish between historical trends and individual preferences here. An adequate historical study of hypermeter would necessarily examine more than eight composers—and would arguably benefit from consideration of contemporaneous music theory and modes of listening, in addition to musical evidence (Grant, 2010).
Our corpus was limited to symphonic repertoire. Future research might examine works for keyboard or chamber groups, though it would be surprising if this association between formal section and hypermetrical regularity were unique to symphonic sonata form. Our approach to hypermetrical irregularity might also be extended to other formal types (building on earlier work, such as Cohn, 1992a, 1992b; McClelland, 2006).
The results of this study are consistent with our hypothesis, though they seem to contradict established ideas about instability in sonata form. Greater hypermetrical regularity in developments might relate, at least in part, to the sequence blocks that define the developmental core. While sequences often deviate from functional tonal principles, they also involve extensive repetition—which increases processing fluency and aesthetic pleasure (Huron, 2013; Margulis, 2014). However, the function of hypermeter in developments might go beyond its association with sequences. In general, hypermetric regularity supports listeners' temporal orientation; in developments, then, it could offer a relatively predictable framework in which unstable events occur. Counterbalancing instabilities in other musical domains, hypermetrical regularity would help listeners navigate the Sturm und Drang that typically marks sonata developments.
ACKNOWLEDGEMENTS
This research was supported by the Music, Cognition, and the Brain Initiative at the University of Western Ontario. We also wish to thank research assistants Cohen Chaulk, Kathryn McDonald, and Jade Roth. This article was copyedited by Tanushree Agrawal and layout edited by Diana Kayser.
NOTES
-
Correspondence can be addressed to: Jonathan De Souza, Don Wright Faculty of Music, Talbot College, University of Western Ontario, 1151 Richmond St., London, ON, N6A 3K7, Canada, jdesou22@uwo.ca.
Return to Text
REFERENCES
- Bakulina, E. (2017). Canons as hypermetrical transitions in Mozart. Music Theory Online, 23(4). https://doi.org/10.30535/mto.23.4.2
- Burnham, S. (1989). The role of sonata form in A. B. Marx's theory of form. Journal of Music Theory, 33(2), 247–271. https://doi.org/10.2307/843794
- Caplin, W. E. (1998). Classical form: A theory of formal functions for the instrumental music of Haydn, Mozart, and Beethoven. New York: Oxford University Press.
- Cohn, R. L. (1992a). The dramatization of hypermetric conflicts in the Scherzo of Beethoven's Ninth Symphony. 19th-Century Music, 15(3), 188–206. https://doi.org/10.2307/746424
- Cohn, R. L. (1992b). Metric and hypermetric dissonance in the Menuetto of Mozart's Symphony in G minor, K. 550. Intégral 6, 1–33.
- Cone, E. T. (1968). Musical form and musical performance. New York: Norton.
- Grant, R. M. (2010). Haydn, meter, and listening in transition. Studia Musicologica, 51(1/2), 141–152. https://doi.org/10.1556/SMus.51.2010.1-2.10
- Hepokoski, J., & Darcy, W. (2006). Elements of sonata theory: Norms, types, and deformations in the late-eighteenth-century sonata. New York: Oxford University Press. https://doi.org/10.1093/acprof:oso/9780195146400.001.0001
- Huron, D. (2013). A psychological approach to musical form: The habituation-fluency theory of repetition. Current Musicology, 96, 7–35.
- Imbrie, A. (1973). Extra measures and metrical ambiguity in Beethoven. In A. Tyson (Ed.), Beethoven Studies (pp. 45–66). New York: Norton.
- Ito, J. P. (2013). Hypermetrical schemas, metrical orientation, and cognitive-linguistic paradigms. Journal of Music Theory 57(1), 47–85. https://doi.org/10.1215/00222909-2017106
- Kamien, R. (1993). Conflicting metrical patterns in accompaniment and melody in works by Mozart and Beethoven: A preliminary study. Journal of Music Theory, 37(2), 311–348. https://doi.org/10.2307/843786
- London, J. (2012). Hearing in time: Psychological aspects of musical meter (2nd ed.). New York: Oxford University Press. https://doi.org/10.1093/acprof:oso/9780199744374.001.0001
- Margulis, E. H. (2014). On repeat: How music plays the mind. New York: Oxford University Press. https://doi.org/10.1093/acprof:oso/9780199990825.001.0001
- McClelland, R. (2006). Extended upbeats in the classical minuet: Interactions with hypermeter and phrase structure. Music Theory Spectrum, 28(1), 23–56. https://doi.org/10.1525/mts.2006.28.1.23
- McKee, E. (2004). Extended anacruses in Mozart's instrumental music. Theory and Practice, 29, 1–37.
- Ng, S. (2012). Phrase rhythm as form in classical instrumental music. Music Theory Spectrum, 34, 51–77. https://doi.org/10.1525/mts.2012.34.1.51
- R Core Team. (2017). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/.
- Rothstein, W. (1989). Phrase rhythm in tonal music. New York: Schirmer.
- Rothstein, W. (1995). Beethoven with and without Kunstgepräng': Metrical ambiguity reconsidered. In C. Reynolds, L. Lockwood, & J. Webster (Eds.), Beethoven Forum IV (pp. 165–193). Lincoln, NE: University of Nebraska Press.
- Temperley, D. (2001). The cognition of basic musical structures. Cambridge, MA: MIT Press.
- Temperley, D. (2003). End-accented phrases: An analytical exploration. Journal of Music Theory, 47(1), 125–154. https://doi.org/10.1215/00222909-47-1-125
- Temperley, D. (2008). Hypermetrical transitions. Music Theory Spectrum, 30(2), 305–325. https://doi.org/10.1525/mts.2008.30.2.305
- Wood Uribe, P. (2011). A. B. Marx's Sonatenform: Coming to terms with Beethoven's rhetoric. Journal of Music Theory, 55(2), 221–251. https://doi.org/10.1215/00222909-1540356
- Zbikowski, L. M. (2017). Foundations of musical grammar. New York: Oxford University Press. https://doi.org/10.1093/oso/9780190653637.001.0001

