INTRODUCTION
THIS article uses theories of African rhythm from ethno/musicology, findings from anthropological research and population genetics, musical analyses based on transcriptions, and computational phylogenetic techniques to compare the intervallic and structural properties of timeline rhythms performed in Pygmy and Bushmen musical cultures. The Pygmy and Bushmen societies considered in this article were, until very recently, semi-nomadic hunter-gatherer people living in sub-Saharan Africa. Pygmy groups (known under a variety of ethnonyms that include Aka, Baka, Efe, Mbendjele,Twa, Gyeli, Bongo and Mbuti) occupy the equatorial forest ranging from Uganda and Rwanda in Eastern-Central Africa across the Democratic Republic of the Congo to Cameroon and Gabon in Western-Central Africa (Olivero et al., 2016). The Bushmen groups (known by ethnonyms that include San, Basarwa, Ju'hoansi, !Kung, Nharo and Khoisan) live in the Kalahari desert straddling Namibia and Botswana, and small numbers also live in South Africa (Lee & Daly, 1999).
Comparative studies of Pygmy and Bushmen musical cultures date back to 1946, when Gilberto Rouget recorded the music of the 'Babenzele' (Mbendjele) Pygmies as part of an expedition to the Ouesso region of the Republic of the Congo. Upon hearing recordings of !Kung Bushmen made by Laurence Marshall in the 1950s, Rouget noted the striking resemblances between Pygmy and Bushmen musics and speculated that they share a common cultural heritage (Grimaud & Rouget, 1956). Since then, numerous anthropologists and ethnomusicologists have documented the relationship between the two musical cultures. The most salient musical characteristics typically cited as common to both groups are the use of ostinato with variations, vocal polyphony, counterpoint, yodelling and singing without words (Frisbie, 1971; Fürniss, 2006; Grauer, 2006, 2009, 2011; Olivier & Fürniss, 1999; Lomax, 1962, 1976).
There is still, however, considerable debate amongst music scholars regarding the connections between Pygmy and Bushmen musics. Some stress the similarities between the two and look to a possible common ancestry, while others place more stress on the differences. Victor Grauer (2009), for example, concludes that Pygmy and Bushmen groups have "many shared stylistic, structural, conceptual, and cultural attributes" and "that both traditions might well stem from a common root, dating to a period deep into the Paleolithic, when the ancestors of both may have formed a single band" (p. 422). By contrast, Susanne Fürniss (2006), when comparing the musical features of Aka Pygmy and Ju'hoansi Bushmen, argues that "although many musical and extramusical features converge and though the acoustic results are very close, the conception that the Jul'hoansi have of their music is radically opposite to the Aka's" (p. 201).
The current study provides a new perspective on this debate by focussing on the analysis of one central musical feature that has received little attention in the literature cited above: timelines 2.
In sub-Saharan African and related musical contexts, timelines have been described by scholars as distinctive and foundational cyclical rhythms (or rhythmic ostinati) that provide the structural and organisational bases for composition and performance, and serve as time-keeping devices for musicians and dancers (Agawu, 2006; Arom, 1991; Kubik, 2010; Peñalosa, 2009). Kofi Agawu (2006) highlights the importance of timelines in research on rhythm in West African ensemble music, arguing that "practically every scholar writing about West African rhythm during the last half century has taken note of time lines" (p. 3). Further, he concludes that "there is, in short, general consensus that time lines are materially real, widely used, and crucial markers of temporal reference in African ensemble music" (p. 3). However, timelines do more than just function as a "temporal reference" for ensembles; they also embody important aesthetic principles. David Locke's (1998) research on the Gankogui timeline rhythm, played on the bell in the performance of West African Gahu music, suggests that the alternating on-beat off-beat structure of this timeline has a powerful "rhythmic potency" that creates "terrific drive" in the music, establishes the "basic rhythmic feel," and adds to the "crucial power of the entire piece" (p. 19). Similarly, David Peñalosa (2009) argues that the clave, a timeline featured in many African-derived musics such as Cuban son, rumba, and salsa, generates a cyclical tension-and-release dynamic: a principle that connects many musics of the Caribbean and South America to their African roots.
Gerhard Kubik (1999) explores this connection further, arguing that timelines are "formidable diagnostic markers for detecting historical connections between certain New World African diaspora musical styles and those of distinctive language zones on the African continent" (p. 56). The reason timelines can be used to reveal the historical connections between related musical styles, Kubik argues, is that their asymmetrical structure is highly resilient to change:
They are immune to all social, cultural, or environmental influences. One can change a time-line pattern's instrumentation, accentuation, speed, starting point, and mnemonic syllables used to teach it, but not its mathematical structure. Any attempt to change that dissolves the pattern (p. 56).
Drawing on Kubik's (1989) work and Arom's (1991) influential theory of rhythmic structures in Central African music, Godfried Toussaint has used computational phylogenetic techniques, typically used by biologists for DNA analysis, to study the evolutionary relationships between sub-Saharan African timelines and those used in a range of musical styles. In numerous publications dating back over ten years 3, his work suggests that phylogenetic analyses can be fruitfully applied in musicological research and that "timelines are effective markers of the structural evolution of rhythms, and their cultural transmission" (Toussaint, Campbell, & Brown 2011, p. 389).
While Toussaint's approach does not consider the relationships between biological and musical evolution, other researchers have used phylogenetic methods to compare the relationships between biological evolution and other cultural phenomena (Mace et al., 2005), such as Turkish textile designs (Tehrani & Collard, 2002), Indo-European folktales (Graca da Silva & Tehrani, 2016), and Hunter-Gatherer marriage practices (Walker et al., 2011). A dedicated comparative study of the structure and phylogeny of timelines used in Pygmy and Bushmen music that considers all of these perspectives (phylogenetic, musical, and cultural) has the potential to provide new insights into the relationship between their musical cultures and the common cultural heritage they may share.
The aim of this article, therefore, is to examine the contemporary and historical relationships between Pygmy and Bushmen musical cultures by drawing on the research of musicologists such as Kubik, Arom, Furniss and Grauer, population geneticists such as Cavalli-Sforza et al. (1994) and Verdu (2014), and others, as well as additional structural and computational phylogenetic analyses of transcriptions of timelines taken from Pygmy and Bushmen recordings. The forthcoming text is presented in four main sections. First, the musical materials, methods, and software used for structural and phylogenetic analyses are detailed. Second, 31 distinct Pygmy and Bushmen timelines are compared in order to quantify the structural similarities and differences between them. This section also examines the connections between the structure of Pygmy and Bushmen timelines and analogous timelines used in other parts of sub-Saharan Africa and beyond. Third, the connections between timelines are considered further by exploring the cultural context in which timelines are performed. The final section makes use of computational phylogenetic analysis of the original 31 timelines as well as research findings from the fields of population genetics and ethnomusicology to uncover possible Pygmy/Bushmen ancestral rhythms.
MUSICAL MATERIALS AND METHODS
A total of 62 timelines were transcribed by the author for analysis in this study. 48 were taken from recordings of Pygmy performances and 14 from Bushmen performances. The transcriptions were made from a mixture of audio and video formats recorded by other researchers in the field. The majority are commercially available on CD and/or online and usually accompany published texts (e.g. Arom, 1991; Kisliuk, 1998). However, one set of recordings of Mbendjele Pygmy music used in this study comes from recent fieldwork by a colleague, Camille Oloa-Biloa, that is not publicly available. In total, I listened to around 1060 individual performances taken from 18 different sets of recordings, which amounts to approximately 45 hours of material, recorded between 1946 and 2014. The cultural groups featured on these recordings were Western Pygmies (BaYaka: Aka, Baka, BaAka, Mbendjele) and Eastern Pygmies (Mbuti) of Central Africa, and San !Kung (Ju'hoansi) and Nharo Bushmen of South Africa 4.
Timelines were selected for further analysis based on the criteria: they were performances by Pygmy or Bushmen groups and not versions performed by neighbouring non-Pygmy/Bushmen; the timelines were reasonably audible within the often dense polyrhythmic texture; the timelines were repeated several times in order to establish a clear cyclical pattern. Through a process of repeated listening/viewing, selected timelines were then transcribed in Western and TUBS (Time Unit Box System) notation 5. Other relevant contextual details (recording date and location, cultural group, region, event, etc.) were also noted, gleaned from CD notes and booklets, websites, publications, and, in the case of Camille's recordings, direct communication with the researcher.
The next step was to identify groups of related timelines from the transcriptions by looking at the number of pulses within each cycle and the number and placement of sounded strokes within that cycle. When an exact match was found, these timelines were treated as a uniform set. Rotation of timelines (the same rhythmic sequence with a different starting point) were retained. This resulted in 31 distinct sets, of which 19 were of Pygmy origin and 12 of Bushmen origin (see Table 1). When comparing the structure of timelines, it was useful to represent each timeline in two additional notational forms: as an interval vector and as a binary sequence. Figure 1 shows the various notational forms used.
The first representation in Figure 1 is Western notation and the second is a commonly-used variant of TUBS where an 'x' represents a sounded stroke and a '.' represents non-sounded pulse. These notational forms were useful when comparing my transcriptions with those in the existing literature. The third representation, an interval vector, is popular amongst some musicologists as it shows the lengths between strokes and indicates intervallic structure (e.g. Arom, 1991; Pressing, 1983). Finally, the fourth representation depicts a rhythm as a binary sequence, used in mathematical and computer-orientated studies of musical rhythm, where a '1' represents a sounded stroke (onset) and '0' a non-sounded pulse (rest) 6.
![Description below. TUBS: [x . x x . x . x . x x .], interval vector: 2 1 2 2 2 1 2, binary: 1 0 1 1 0 1 0 1 0 1 1 0](https://emusicology.org/index.php/EMR/article/download/5823/version/5309/4966/19722/5823_Poole_Figure1.png)
Figure 1. Four notational representations of one timeline rhythm: Western notation; TUBS; interval vector; and binary.
Binary representations were used in this study for the comparison of timelines in conjunction with the well-known edit-distance or Levenshtein-distance algorithm (Levenshtein, 1966). The edit-distance is defined as the minimum number of edits (substitutions, insertions, and deletions) necessary to transform one sequence of symbols to another. Thus, the edit-distance provides a measure of similarity between the binary representations of two rhythms. While there are many algorithms that could be used to measure the distance and similarity between musical objects (Toussaint, 2013, pp. 247-256), the edit-distance shows a high correlation with human similarity judgments in experimental conditions (Post & Toussaint, 2011; Toussaint, Campbell, & Brown, 2011). The edit-distance model was implemented in MATLAB using existing code (Ahmadzadeh, 2012), yielding a distance matrix for every pair of rhythms (Appendix B, available at: http://hdl.handle.net/1811/85870).
Finally, phylogenetic trees were generated from the distance matrix in the program SplitsTree v4.13.1 (Huson & Bryant, 2006) to provide a visual representation of the distance relationships between timelines and to look for possible ancestral rhythms. The tree was generated from the distance matrix using the BioNJ function, an agglomerative algorithm that accepts a distance matrix and uses a first-order model of the variances and covariances to estimate evolutionary distances. It does this by iteratively picking a pair of taxa (rhythms in this case), creating a new node, which represents the cluster of these taxa, and reducing the distance matrix by replacing both taxa by this node (Gascuel, 1997). The BioNJ function was chosen because it has been used successfully in conjunction with the edit-distance model as an effective measure of rhythmic similarity (Toussaint, Campbell, & Brown, 2011; Toussaint, Matthews, Campbell, & Brown, 2012).
The SplitsTree program also calculates the least squares, or LSFit, which provides a measure of the goodness-of-fit between the distance matrix and the tree. This is obtained by dividing the sum of all approximated distances in the splits tree by the sum of the original distances in the data set (Guastavino et al., 2009; Huson, 1998). If the index is very close to 100%, the tree represents the distance matrix faithfully. Lower fit values represent a poorer correspondence between the tree and the distance matrix. The musical materials and results of this analysis are discussed below.
STRUCTURAL SIMILARITY AND DIFFERENCE
This section examines the structural similarities and differences between Pygmy and Bushmen timelines and how these structural properties might be explained by existing models of rhythm. Table 1 shows the 31 distinct sets of timelines used for analysis, ordered by the cultural group: Pygmy and Bushmen. A further sub-group differentiates between timelines that divide the tactus (primary underlying pulse) into three and those that divide the tactus into two or four, typically referred to by scholars as ternary and binary or simple and compound rhythms (London, 2004, p. 18). However, I make use of the alternative terms triple-pulse and quadruple-pulse in Table 1 as it more accurately reflects the transcriptions used here. Whether a timeline was triple or binary/quadruple was determined primarily by listening to performances and noting the subdivision of the pulse suggested by the placement of the strokes. A secondary source, and means of checking my interpretation, was the transcriptions in the accompanying literature. Scholars such as Arom (1991), Kisliuk (1998), and Olivier (2001) helpfully provide numerous transcriptions in books and articles in TUBS or Western notation that indicate the timeline pulse subdivision, as well as the starting point and rotations of rhythms.
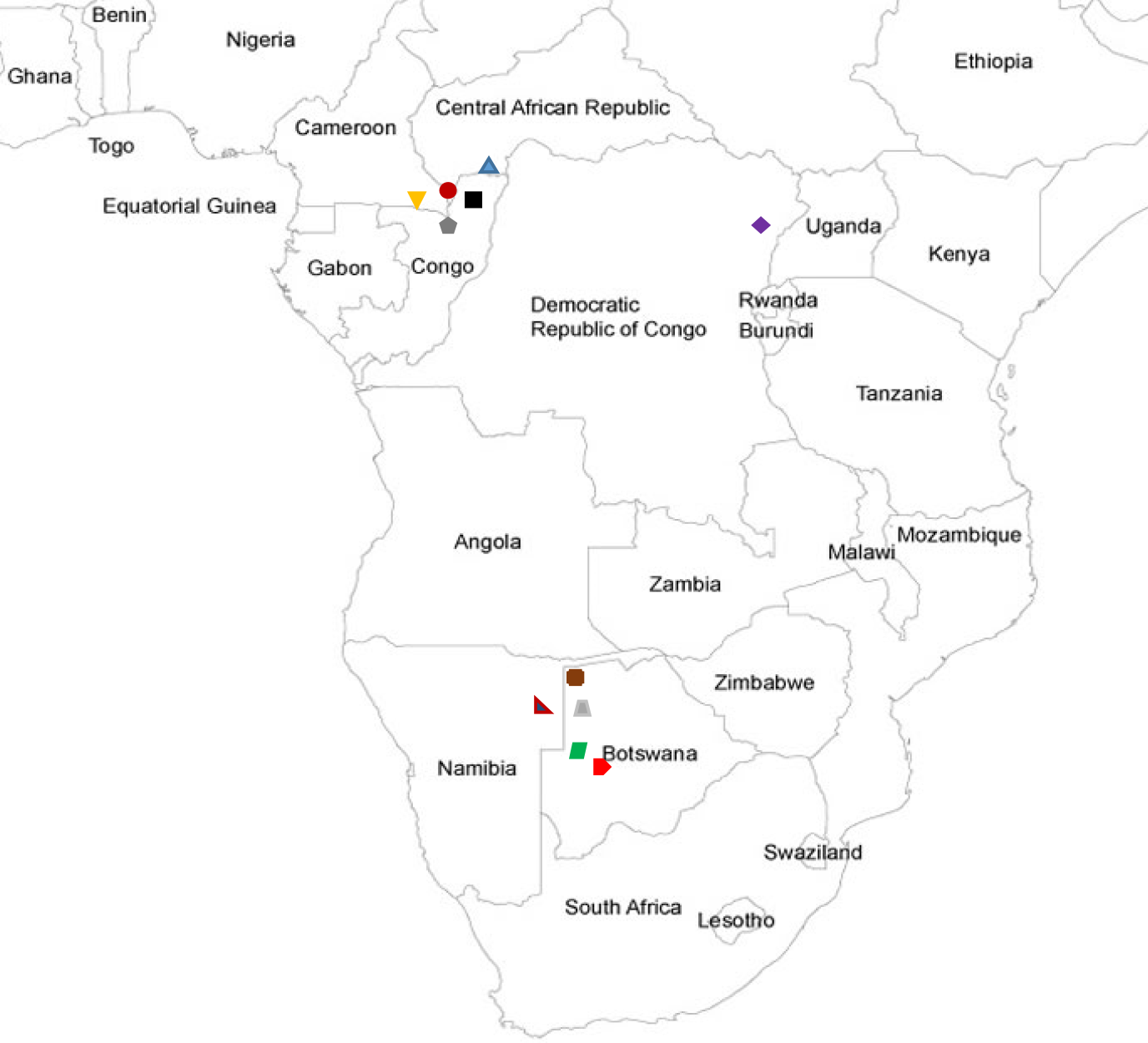
Numbers have been added in the first column to differentiate sets of timelines and provide easy reference. The second column shows the name of the cultural groups that performed the music. Following Lewis (2014, p. 221), I use the term 'BaYaka' to represent the west-central African Pygmy groups Mbendjele, Baka, and Aka who occupy the forest west of the Ubangi River in the Central African Republic, Congo and Cameroon. The term 'Mbuti' is used to represent the Kango-Sua, Efe, and Asua groups that occupy the Ituri forest in the north-eastern region of the Democratic Republic of th Congo (Fürniss, 2014, p. 188). The term 'San' is used to encompass the Ju'hoansi, Nharo, and !Kung groups who live in and around the Kalahari desert in Botswana and Namibia (Lee & Daly, 1999). See Figure 2 below for a map of recording locations. The third column is a transcription of timelines over one cycle in TUBS notation and the fourth is an intervallic representation based on transcription. Column five (n) is the number of timelines transcribed from the recordings with totals for each group and column six (p) is the number of pulse per cycle.
| Symbol | Cultural Group | Region | Timeline Number |
|---|---|---|---|
 | BaYaka | Lobaye, CAR | 1, 3, 6, 7, 9, 10, 11 |
 | BaYaka | Dzanga-Sangha, CAR | 1, 2, 5, 12, 13, 17 |
 | BaYaka | Sangha, Congo | 10, 13 |
 | BaYaka | Likouda, Congo | 1, 2, 3, 6, 8, 13, 14, 16, 19 |
 | BaYaka | South East Cameroon | 4, 6 |
 | Mbuti | Ituri, DRC | 15, 18 |
 | San | North West Botswana | 20 |
 | San | Western Kalahari | 21 |
 | San | Nyae Nyae, Namibia | 22, 23, 27, 29-31 |
 | San | North West Kalahari, Botswana | 24, 25, 26 |
 | San | Central Kalahari, Botswana | 28 |
Figure 2. The recording locations of the cultural groups and timelines studied.
| Pygmy triple-pulse | |||||
| No. | Cultural Group | Rhythm (one cycle) | Interval Vector | n | p |
|---|---|---|---|---|---|
| 1 | BaYaka | x.x.x.xx.x.x | 2221221 | 6 | 12 |
| 2 | BaYaka | x.x.xx.x.x.x | 2212221 | 3 | 12 |
| 3 | BaYaka | x.x.x.x.x.x. | 222222 | 4 | 12 |
| 4 | BaYaka | x.x.x.x.x..x.x.x.x.x.x.. | 22223222223 | 1 | 24 |
| 5 | BaYaka | x.x.x..x.x.x x.x.x..x.xx. | 223221223212 | 1 | 24 |
| 6 | BaYaka | x.x.x..x.x.. | 22323 | 4 | 12 |
| 7 | BaYaka | x.x..x.x.x.. | 23223 | 1 | 12 |
| 8 | BaYaka | x.x.x.xx.x.. | 222123 | 1 | 12 |
| 9 | BaYaka | x.x.x.x.xx.. | 222213 | 1 | 12 |
| 10 | BaYaka | x.x.x.x.xx.x.x.x.x.x.xx. | 2222122222212 | 9 | 24 |
| 11 | BaYaka | x.x.x.x.x.xx.x.x.x.x.xx. | 2222212222212 | 1 | 24 |
| 12 | BaYaka | x.x.x.x.x.xx.x.x.x.x.x.x | 2222212222221 | 1 | 24 |
| 13 | BaYaka | x.x.x.x.x.x.xx.x.x.x.xx. | 2222221222212 | 8 | 24 |
| 14 | BaYaka | x.x.x.xx.x.x.xx.x.x.x.x. | 2221222122222 | 1 | 24 |
| quadruple-pulse | Total | 42 | |||
| 15 | Mbuti | x.x…x…x.x… | 24424 | 1 | 16 |
| 16 | BaYaka | x..x..xx..x.x… | 331324 | 2 | 16 |
| 17 | BaYaka | x..x..x…x.x… | 33424 | 1 | 16 |
| 18 | Mbuti | x…..x…x.x… | 6424 | 1 | 16 |
| 19 | BaYaka | x..x..x.xx..x..x..x.xx..x..x..x. | 3321333213332 | 1 | 32 |
| Bushmen triple-pulse | Total | 6 | |||
| 20 | San | x.x.x.x.x.x. | 222222 | 2 | 12 |
| 21 | San | x.x…x.x.x. | 24222 | 1 | 12 |
| 22 | San | x.x..x… | 234 | 1 | 9 |
| 23 | San | x.x…x.. | 243 | 1 | 9 |
| 24 | San | x.x.x.x.. | 2223 | 1 | 9 |
| 25 | San | x..x..x.x… | 3324 | 1 | 12 |
| quadruple-pulse | Total | 7 | |||
| 26 | San | x.x…x…x.x… | 24424 | 1 | 16 |
| 27 | San | x.x…x.x……. | 2428 | 1 | 16 |
| 28 | San | x…..x.….x… | 664 | 2 | 16 |
| 29 | San | ……x…x…x. | 448 | 1 | 16 |
| 30 | San | x…x…..x…x.…. | 4646 | 1 | 20 |
| 31 | San | x..x..x. | 332 | 1 | 8 |
| Total | 7 |
Rhythmic Oddity
The first theory considered here that holds some relevance when comparing the structure of timelines in Table 1 is the concept of a 'rhythmic oddity,' a term coined by ethnomusicologist Simha Arom in his influential study of music in Central Africa, including an analysis of the rhythms used by Western Aka Pygmies (Arom, 1989, 1991). According to Arom (1989), timelines are classified as a rhythmic oddity when their content is "segmented as closely as possible to the central dividing point," resulting in two parts "composed of an odd number of minimal values…they respect a rule that might be called 'half – 1 / half + 1" (p. 94). One of the rhythms he uses to demonstrate this principle is what he calls the diketo timeline, shown in TUBS notation in Table 1: number 10 [x.x.x.x.xx.x.x.x.x.x.xx.] 2222122222212. This same timeline is shown in Western notation in Figure 3.
Arom's example shows that when the 24-pulse diketo timeline is segmented as close to the middle as possible – between pulses 11 and 12 – the two units are composed of intervals of half – 1 / half + 1, 12 – 1 / 12 + 1, or 11 / 13. Arom (1989) argues that this asymmetrical structure characterizes the diketo timeline as a rhythmic oddity, adding that this is "a particular form of asymmetry that is frequently found in Central Africa" (p. 94).
If I have interpreted Arom correctly, most of the Pygmy timelines in Table 1 conform to his model and are rhythmic oddities – excluding numbers 3, 9, 15, 17 and 18. Notably, none of the Mbuti Pygmy and Bushmen timelines appear to conform to Arom's model. This suggests that the rhythmic oddity model is relevant to the timelines used by Pygmy groups from the Western region of Central Africa but is not applicable to the San Bushmen, who live in Namibia and Botswana some 2500km to the south, or Mbuti Pygmies who reside 1600km to the west.
Whether Arom's model is of use as a more general comparative tool for rhythms outside Central Africa is an open question. The first limitation is that only rhythms with an even number of pulses per cycle can be rhythmic oddities, such as the 24-pulse diketo timeline in Figure 3, thus excluding those with 9-pulse per cycle such as numbers 22-24 in Table 1. This is because, as Godried Toussaint (2013) points out, "an odd number is not evenly divisible by two" (p. 85). In the same chapter, Toussaint provides a generalized version of Arom's model, one that "measures the amount of rhythmic oddity a rhythm possesses. This function (rhythmic oddity) depends on the number of violations of the rhythmic oddity property present in a rhythm" (p. 88). Toussaint's work suggest that, despite its limitations, a more generalized interpretation of this model is useful when comparing certain timelines found in sub-Saharan Africa and the African diaspora 7.
A Generative Approach
Generative models of African rhythm have received considerable attention in academic literature and provide some important insights that are relevant here. In his review of the various approaches to the rhythmic analysis of African music, Kofi Agawu (2006) writes: "of the numerous competing approaches to the analysis of African rhythm in general and time lines in particular, the one most consonant with African ways of proceeding is a generative approach. A generative approach recognizes a model and its elaborations, a deep structure – be it real or postulated – that supports a ruling surface" (p. 28). Taken as a whole, the research to which Awagu refers, namely that of Agawu (1995), Anku (2000), Arom (1991), Locke (1996), Pressing (1983), and Toussaint (2003), suggests that many timelines used in sub-Saharan African musics may be generated from a few basic patterns.
Jeff Pressing (1983), for example, argues timelines "may be derived from a few patterns (primarily 22323 (or 2212221), 322, 323) by one or more of the following rules of transformation:" (a) cyclic permutation; (b) element fission or fusion; (c) complementation or figure-ground reversal; (d) maximally similar analogue approximation; and (e) element permutation (p. 52). Using example timelines from West African, Afro-Latin and Balkan musics, he writes that transformations (a)-(d) are "common and basic" and "preserve the pattern in a holistic sense" (p. 52). Only (e), element permutation, "involves structural derangement that is more drastic that the others" (p. 52). More recently, Godfried Toussaint (2013) has demonstrated how certain African, Afro-Caribbean and other timelines found in North American popular music can be constructed algorithmically from seed rhythms using mathematical principles. One such rhythm is the three-against-two (3:2) or 222 [x.x.x.] pattern that "by itself is already imbued with a great deal of rhythmic power, as evidenced by its widespread popularity all over the world" (p. 214; 8). David Peñalosa (2009) argues that the three-over-two (3:2) triple-pulse cross rhythm "is the most basic rhythmic cell in clave-based music" (p. 22), one that plays a fundamental role in sub-Saharan African and Afro-Cuban music and dance: "In many folkloric dances, the steps emphasize the main beats, while the drums emphasize cross-beats. In this way, the dancers and drummers collectively create 3:2" (p. 24).
Similarly, Novotney (1998) suggests that timelines in West African (mainly Ghanaian and Nigerian), Afro-Cuban, and other West African-derived musics are based on the foundational 3:2 (three-against-two) triple-pulse pattern. Moreover, he argues that the structure of this "key pattern" is a universal phenomenon reflected in nature, mathematics, architecture, and music. Drawing on the work of composer and music theorist Iannis Xenakis, he writes:
I've confirmed that the 3:2 relationship is observed as a natural phenomenon that is not exclusive to any race, culture, or geographic region. In fact, it is not an invented phenomenon but, instead, an observed and imitated one. Through time, various musical and non-musical structures have been founded on the same basic operating principle of proportional relationships. Xenakis believes that a comprehensive theoretic vision would account for phenomena generated by these relationships in all musics. I thoroughly agree with Xenakis on this crucial point. A comprehensive theoretic vision, without bias, must account for proportional phenomena from the Greeks, to the West, to the East, and (most importantly for this document) to Africa. (pp. 199-200).
The work of Pressing, Toussaint, Peñalosa, and Novotney indicates that the 3:2 pattern forms the structural backbone of two of the most widely used African timelines: [x.x.x..xx.x.x.x] 2212221 and [x.x.x..x.x..] 22323. Both have been referred to by a number of researchers as the "standard pattern" or African "signature rhythm" due to their frequent use in many parts of Central and West Africa (e.g. Agawu, 2006; Jones, 1959; King, 1960; Kubik, 2010). The 2212221 pattern is used by people in various African regions: "Guinea Coast with its speakers of Akan, Ewe, Fo, Yoruba, and so on; west-central Africa from eastern Nigeria to Gabon, Congo, Angola; southern Congo-Zaire, into Zambia; and to southeast Africa in a broad belt, covering Zambezi and Ruvuma cultures" (Kubik, 1999, p. 60). The 22323 triple-pulse pattern, and versions thereof, has been found among the Yourba, Ewe, Ila, and Tonga people of West and Central Africa (Jones, 1959, pp. 211-212). In Fürniss' (2014) study of Aka and Baka Pygmy groups, she argues that the "standard pattern" 22323 and its augmentations form part of a "common stock of rhythms that are combined in various ways according to the repertoire. The stock of rhythms is exactly the same in both cultures" (p. 203).
In the current study, the 2212221 and 22323 timelines are used by BaYaka (Baka, Aka, and Mbendjele) Pygmy groups (numbers 2 and 6 in Table 1). Furthermore, the 3:2 pattern [x.x.x.] is evident in the majority of Pygmy and Bushmen triple-pulse timelines. Specifically, almost all (12 of 14, all but numbers 2 and 7) triple-pulse Pygmy timelines feature this stroke pattern: [x.x.x.]. Of the Bushmen triple-pulse timelines, half (3 of 6, numbers 20, 21 and 24) feature the same 3:2 pattern. Interestingly, the only structurally identical triple-pulse timeline used by both Pygmy and Bushmen groups contains nothing but two repeated 3:2 patterns [x.x.x.x.x.x.] 222222 (numbers 3 and 20 respectively).
Some quadruple-pulse timelines also contain the 3:2 pattern: two of the five Pygmy timelines (numbers 17 and 19) begin with [x..x..x.] and a single Bushmen timeline (number 8) consisted of just [x..x..x.]. It is notable that the two Mbuti Pygmy timelines (numbers 15 [x.x…x…x.x…] and 18 [x…..x. ..x.x…]) do not contain the 3:2 pattern. As the Mbuti groups live approximately 1600km away from the BaYaka in the eastern-central region, this might be indicative of an east-west divide. Susanne Fürniss (2014) has examined the musical diversity of different Pygmy groups in the Congo Basin and offers some insight on this issue:
What is striking about the Mbuti in comparison with western Pygmies is the relatively slow pace of the music. Also, all Mbuti music is based on a binary metricity that is not marked by hand clapping. Musical periods are very short, usually based on two or four beats, but sometimes eight or sixteen (p. 192).
The absence of the 3:2 pattern in Mbuti timelines echoes Fürniss' comments that there are periodic and structural differences to be found in eastern and western Pygmy timelines. A generative approach might explain some of these differences. Compare, for example, timeline number 17 [x..x..x…x.x..], the "standard pattern" used by the BaYaka, and number 18 [x…..x…x.x…] used by the Mbuti Pygmies. In terms of stroke patterns, the difference between these timelines is the addition of a stroke at pulse position 4. This may be indicative of what Pressing calls "element fusion," or perhaps element deletion. How and why these transformations may have occurred is unclear and worthy of further investigation. It does, however, highlight how a generative approach is a useful starting point when comparing timelines used by cultural groups with little or no contact that are separated by large geographical distances.
As well as the 3:2 pattern, other related rhythmic cells stand out when comparing the timelines in Table 1. First, all triple-pulse Pygmy and Bushmen timelines start with [x.x], apart from number 25, which has this pattern in the second half of the rhythm. The next most common cell is either [.x.], [..x] or [.xx], with the occasional […] and [x..] cell found in Bushmen timelines – numbers 21, 23 and 25. The combination of cells [x.x] and [.x.], [..x] or [.xx] at the start of these timelines creates a syncopation that seems to be a fundamental feature of the triple-pulse Pygmy and Bushmen timelines in Table 1.
Quadruple-pulse Pygmy and Bushmen timelines also feature various commonly used rhythmic cells. All 11 start with either [x.x.], [x..x] or [x…], except number 29, which starts with [….]. The majority (9 of 11) are followed by [..x.], with numbers 16 and 30 featuring the cells [..xx] and [x…]. Similar to the triple-pulse timelines, these cell combinations found in a quadruple-pulse framework mark the beginning of the timeline with an on-beat (the 'one') followed by a variety of off-beat patterns that create a sense of syncopation. Chernoff (1991) argues that these rhythmic phrases found in timelines like the "standard pattern" and its many variants, whether perceived in triple-pulse or quadruple-pulse meter, are part of the rhythmic aesthetic of many African dance musics, an aesthetic that helps to establish a sense of "lift," "energy," "participation," and "movement" in the music (pp. 1099-1101).
Maximal Evenness
Another concept used to explain the properties of pitch and rhythm that has received much attention in music theory is 'maximal evenness' (Clough & Douthett, 1991; London, 2004; Rahn, 1996; Taylor, 2012; Toussaint, 2013). In simple terms, a rhythm is maximally even if the strokes are distributed as evenly as possible within the cycle. Hence, using two contrasting examples from Table 1, numbers 3 and 20 [x.x.x.x.x.x.] 222222 are a maximally even distribution of six strokes over a 12-pulse cycle, whereas number 29 [……x…x…x.] 448 is not an even distribution of three strokes of over a 16-pulse cycle. Given that three strokes do not divide equally into a 16-pulse cycle without remainder, a maximally even version would be, for example, [x….x….x…..] 556, [x….x…..x….] 565, or [x…..x….x….] 655.
Godfried Toussaint has attempted to provide a more precise characterization of maximal evenness by measuring the similarity of timeline rhythms using mathematical principles. His work suggests that many widely-distributed African and Afro-Cuban timelines can be categorized as maximally even or 'almost maximally even' (Toussaint et al., 2012, p. 29; Toussaint, 2013, pp. 121-127). A notable timeline that illustrates the potential importance of these concepts is number 17 [x..x..x…x.x…] 33424 used in BaYaka Pygmy music. This rhythm is referred to as 'son clave' or 'clave son' in Afro-Cuban contexts and Toussaint argues that this is a particularly successful and "good" timeline because the strokes are almost evenly distributed but the stroke placements also possess a degree of irregularity, which contributes to its widespread appeal: "to succeed as a musical timeline…a rhythm must be somewhat asymmetrical; it must possess some irregularity; and it must contain an element of surprise…the clave son strikes a balance between too much and too little regularity, but leaning closer to regularity than irregularity" (Toussaint, 2013, p. 280).
Justin London provides a more psychologically-orientated perspective on maximal evenness and timelines. Taking, for example, number 6 [x.x.x..x.x..] 22323 or the "standard pattern," found in BaYaka and many sub-Saharan musics, he argues, similar to Toussaint, that a degree of irregularity is seen in many widely-used timelines: "…maximal evenness cannot always be maintained on every subcycle, nor can ambiguities be wholly eliminated…it becomes clear that we do not (and indeed cannot) require perfect maximal evenness" (London, 2004, p. 132). Furthermore, London (2004) postulates that maximal evenness serves as a global constraint on metric pattern formation – especially cyclical rhythms – ensuring that "our attentional energies are effectively distributed over the course of a metric cycle, so that we can efficiently attend to and differentiate among events of varying salience" (p. 114). He continues by arguing that, in addition to optimizing the attention of musicians and listeners, maximally even metric patterns are also linked with efficient motor behaviours:
Maximal evenness is also yoked to the timing of motor behaviors, as the symmetry or near-symmetry of maximally even meters prevents the mixture of short/rapid intervals with longer, slower ones. This avoids meters that would have correlates with herky-jerky movement patterns. To put it another way, well-formed meters serve to guide smooth, well-formed motor behaviors… (pp. 162-163).
How then, might the principle of maximal evenness explain some of the relationships between timelines found in Pygmy and Bushmen music in Table 1? Among the triple-pulse patterns, Pygmy timelines contain intervals between strokes of 1, 2 and 3, and exclusively contain "1s." Importantly, "1s" are always isolated, never appear consecutively, and are maximally or almost maximally evenly distributed throughout the rhythmic cycle. Bushmen timelines do not contain "1s" and some (numbers 21, 22, 23, 25) feature larger intervals between strokes of 4. Numbers 20 and 24 are maximally even, while numbers 21, 22, 23, 25 are more irregular and almost maximally even.
Among the quadruple-pulse patterns, Pygmy timelines feature intervals between strokes of 1, 2, 3, 4, and one 6 (number 18). Similar to the triple-pulse timelines, "1s" and other smaller intervals are isolated and maximally evenly distributed throughout the cycle. Bushmen timelines do not feature "1s" but do feature the higher intervals of 6 and 8. Generally, the lower intervals are separated by the higher ones and are almost maximally evenly distributed throughout the rhythmic cycle.
These features highlight important similarities and differences between Pygmy and Bushmen timelines in Table 1. Timelines vary in pattern length, containing 8, 9, 12, 16, 20, 24, or 32 pulses (column 'p') and also vary in relative density, with Pygmy timelines being denser, as indicated by the smaller interval between strokes. All timelines, however, appear to be organized according to the principles of maximal evenness. Some timelines are perfectly even (e.g. 222222) but the majority are best characterized as almost maximally even as they contain a degree unevenness or irregularity. Furthermore, maximal evenness not only serves as an important point of connection between Pygmy and Bushmen cultural groups, but also suggests that there are structural similarities between Pygmy/Bushmen timelines and those used in other parts of sub-Saharan Africa and related musics around the world, such as the "standard pattern" and son clave.
To summarise, the 'rhythmic oddity' model proposed by Arom is useful in explaining the structural connections between timelines of Pygmy groups from the Western region of Central Africa but not Mbuti Pygmy and Bushmen timelines. The models that most readily explain the structural relationships between western and eastern Pygmy and Bushmen timelines are generative theory and maximal evenness. A generative approach highlights how many Pygmy/Bushmen and African and African-derived timelines feature commonly used rhythmic cells or units. These cells, such as the 3:2 pattern, form the structural basis of many timelines and create a sense of syncopation that is part of the fundamental aesthetics of African dance musics. The principle of maximal evenness highlights further the structural connections between Pygmy and Bushmen timelines by suggesting that regular and almost regular rhythms are preferred in both musical traditions. Moreover these models draw important connections between Pygmy/Bushmen timelines and the ubiquitous "standard patterns" used in other parts of sub-Saharan Africa and related musics around the world. The following section aims to explore further the relationships between these timelines by considering the musical and cultural context in which timelines are performed.
CULTURAL CONTEXT AND RESILIENCE
Some Cultural Context
It is noteworthy that the cultural contexts in which timelines are used are extremely varied. Take, for example, the triple-pulse timeline seen in numbers 3 and 20, which is used by BaYaka Pygmy and San Bushmen groups and features the pattern [x.x .x. x.x .x.] 222222 – clearly a repetition of the [x.x .x.] 222 'seed' rhythm. In BaYaka contexts, timeline number 3 is used in elamba, djoboko and ndambo performances. According to Michelle Kisliuk's (1998) ethnographic accounts based on her fieldwork with the BaAka Pygmies in the Loyobe region of the Central African Republic, elamba is a women's dance that "is not connected with any special occasion or purpose" and is largely for enjoyment, but is based on an older hunting ritual; Djoboko, sung by men and is danced "most earnestly at funerals, especially for the passing of an elder woman" (p. 68). (N)dambo, she writes, is a related "BaAka eboka [music-dance event] associated with spear hunting" (Kisliuk,1998, p. 220).
Turning to the Bushmen context, timeline number 20 is used in kudu and mongongo performances. According to John Brearley's (1982) ethnographic research with the Ju'hoansi of North-West Botswana, mongongo is a music-dance event used to express happiness on finding nuts on the mongongo tree. Amongst the Ju'hoansi of North-Eastern Namibia, kudu (a type of antelope hunted by Bushmen) music has a curative function performed for healing illness (Olivier, 2001, p. 14).
A similar situation is evident with the quadruple-pulse timeline [x.x. ..x. ..x. x…] 24424, numbers 15 and 26, which is used by Mbuti Pygmies and San Bushmen. In Mbuti contexts, this timeline is used in music associated with Elephant hunting. In Colin Turnbull's (1961) anthropological research with the Mbuti Pygmies, he writes that Elephant-hunting songs tell how a particular Elephant was killed but also "might be an act of atonement, a death festival for the elephant" (p. 2). He continues by describing how these songs are musically very similar to another type of song, molimo: "It is difficult to trace the origin of this distinctive type of song, but it is closest to the sacred molimo songs of the Mbuti, sung in times of great crisis, particularly death. Sometimes, indeed, these elephant hunting songs are almost indistinguishable from molimo songs." (p. 2)Elsewhere he describes the molimo music-dance festival as a "magico-religious" event, which relates to many aspects of Mbuti life such as death, hunting, sickness and rejoicing the forest (Turnbull, 1965, pp. 260-267).
For the San Bushmen of Botswana, the 24424 timeline is associated with 'treesdance' music. With reference to 'treesdance,' Richard Katz, like Turnbull, hints at how new music-dance forms are created from older ones. In the sleeve notes to his 1968 field recordings he writes:
Trees Dance. A !kia dance recently created by a young San man, which incorporates elements from pastoral neighbors. With a solo emphasis differing from the traditional dance, the creator sings his songs rapidly, barely forming his words, and the dance troop of women responds with singing and clapping. Others in the camp are not active participants in the dance. Though the dance creator does !kia, healing is not emphasized (Katz et al., 1982, p. 3).
These examples illustrate two important points with regard to the cultural context in which timelines are featured. First, individual timelines are multi-purpose and do not appear to be associated with one single song category, event, or occasion, both within and across Pygmy and Bushmen cultures 9. Second, these examples reflect a theme that runs through much of the anthropological and ethnomusicological literature on Pygmy and Bushmen music and culture: that is, far from being frozen or static, they continue to adapt existing musical materials present within their own musical heritage and incorporate those from their Pygmy/Bushmen and non-Pygmy/non-Bushmen (mainly Bantu-speaking) neighbours to create new ones (Bleek, 1928; England, 1967, 1995; Fürniss & Joiris, 2011; Hewlett, 2014; Kisliuk, 1998; Marshall, 1976; Olivier, 1998, 2001; Sarno, 1993, 1995; Turnbull, 1961, 1965). The remainder of this section considers findings from this literature that highlight the nature of continuity and change in Pygmy culture, and explores the ideas that the core structure of timelines may be highly resilient musical features.
Continuity, Change and Resilience
In her fieldwork in the Lobaye region (CAR), Kisliuk (1998) describes how BaAka Pygmies incorporate new musical material into existing repertoires, eventually creating an unmistakeably BaAka style (pp. 167-197). She writes that the melodies of Christian hymns and other songs are transformed through improvised performance into yodelled, cyclical forms: "BaAka eventually treat hymns much in the way they treat a new BaAka melody – over months and years elaborating on a theme until eventually it is engulfed in a flurry of kaleidoscopic improvisations, countermelodies, and elaborations" (p. 188). Building on Kisliuk's research, Lewis (2013) argues that, despite being separated by large geographical distances and speaking a different language, Mbuti and BaYaka Pygmies share common "musical foundational schemas" that "may have extraordinary resilience…this resilience is due to their special aesthetic, incorporative, adaptive, and stylistic qualities which ensure continuity despite change" (p. 64). The central focus of the work of Kisliuk and Lewis is not timelines. Instead they focus on singing/song style (vocal polyphony and yodelling) and the organising socio-aesthetic principles that underpin Pygmy musical culture and ritual practices. However, these propositions complement the argument put forward by Kubik (1999) that sub-Saharan African timelines are also foundational musical features that are highly resilient to change: "their mathematical structures are cultural invariables, i.e., their mathematics cannot be changed by cultural determinants. They are immune to all social, cultural, or environmental influences" (p. 56).
The data collected as part of the current study reinforces Kubik's argument. Take, as an example, timeline number 13 [x.x .x. x.x .x. xx. x.x .x. xx.] 22222212222212 used by BaYaka Pygmies groups in the Dzanga-Sangha region in CAR, and the Likouala and Sangha regions in Congo (see Table 1 and Figure 2), located some 100km apart. This timeline featured in eight separate audio tracks, recorded in 1946, 1987, 2013, and 2014, and was used in a variety of events: djoboko (or joboko), rejoicing after returning from a hunt; edjengi, hunting rituals (Kisliuk, 1998); limboku, celebrating female power and sexuality (Sarno, 2016); bolobe, net hunt ceremony/entertainment (Sarno, 1995); ngoku, net hunting/other events; and nganga, healing (Lewis, 2002). The 22222212222212 interval structure of this timeline is identical in all of these recorded examples.
A second example is the 22323 or "standard pattern," used by BaYaka groups in Cameroon, Loyabe, Likouala, and Dzanga-Sangha regions (numbers 6 and 17 in Table 1). There is some historical evidence that the fundamental structure of this timeline has remained intact since the early thirteenth century. Godfried Toussaint describes how a book written in around 1252 by Arabic scholar Safi al-Din details a binary version (33242) of the 22323 pattern represented in a mnemonic syllable system. Toussaint writes, "we can be pretty certain that the clave son in its binary form [3-3-4-2-4] existed in Baghdad as early as the thirteenth century" (2013, pp. 297-298), and speculates that this timeline may have originated in Central Africa and migrated to Baghdad.
These are, of course, isolated examples and a dedicated ethnomusicological study is needed to examine continuity and change across a greater number of Pygmy and Bushmen performances to produce a more robust theory. However, taken together with the findings in this section, it seems unlikely that the structure of timelines, like other foundational musical features, have changed drastically. Variation on the basic stroke patterns through improvisation or adaption in order to accommodate new musical influences is likely but deep-rooted radical change to their fundamental structure seems improbable. The oldest recording used in my analysis is from 1946 and the historical evidence dates back, at the very most, to the thirteenth century. The final section attempts to use phylogenetic techniques to open a window onto a more distant past by looking at possible early ancestral rhythms.
PHYLOGENETIC ANALYSIS AND ANCESTRAL RHYTHMS
This section discusses the results of computational phylogenetic analysis on the 31 timeline groups in Table 1. Following the distinction shown in Table 1 between rhythms that divide the tactus into three or four, Figure 4a-c shows three rooted phylogenetic trees. Figure 4a shows just quadruple-pulse timelines; Figure 4b shows triple-pulse timelines; and Figure 4c shows quadruple-pulse and triple-pulse timelines together. The resultant phylogenetic trees provides a visual representation of the hierarchical distance between timelines and their cluster relationships. Each node in the tree is labelled with a "BP," "MP," or "B" to identify BaYaka Pygmy, Mbuti Pygmy or Bushmen timelines, followed by a shortened label (to improve readability), then, for example, 'T12' or 'Q16,' (triple-pulse or quadruple-pulse, and the pattern length/number of pulses per cycle) and the assigned number identifier (in brackets) taken from Table 1. BaYaka Pygmy labels are shown in black, Mbuti Pygmy labels are in red, and Bushmen labels are blue.
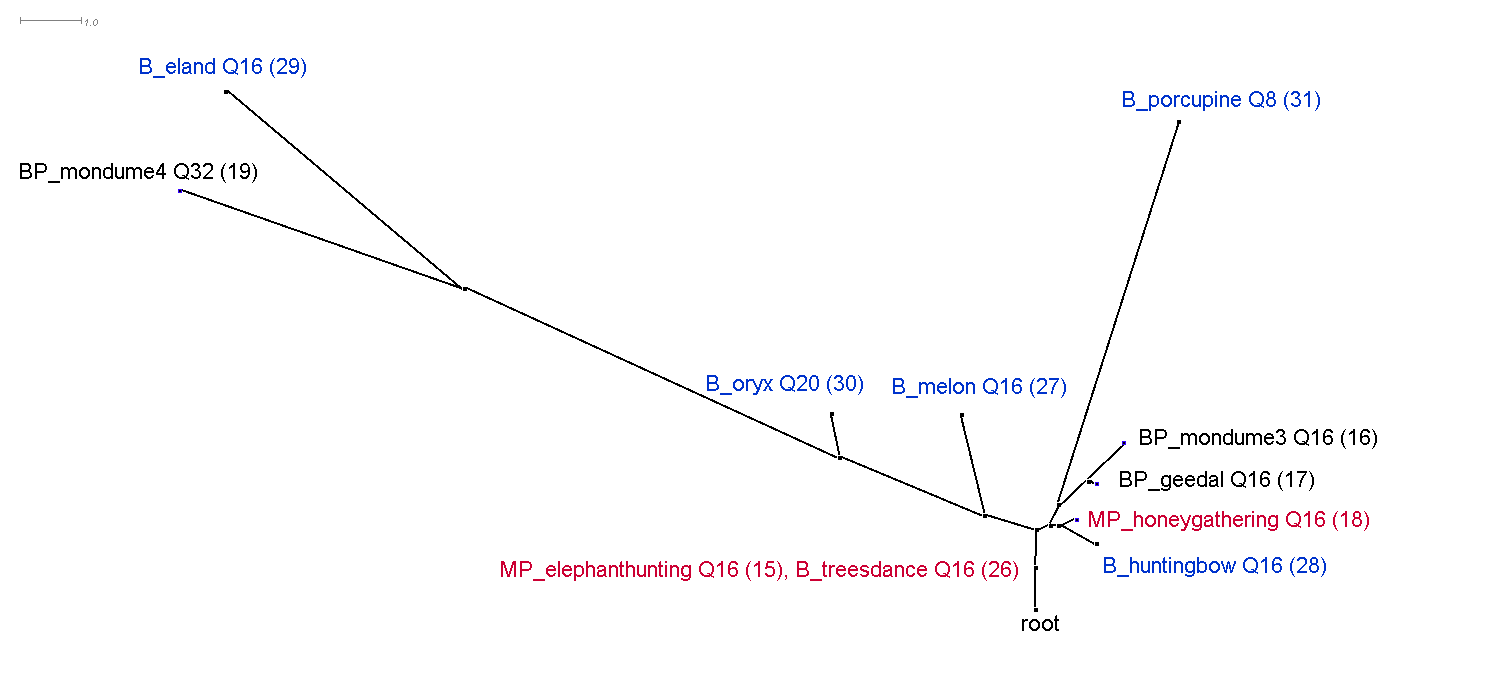
Figure 4a. Rooted phylogenetic tree constructed from a distance matrix generated by the edit-distance algorithm (Appendix B, available at: http://hdl.handle.net/1811/85870) of the quadruple-pulse timelines from Table 1. "BP" = BaYaka Pygmy (black), "MP" = Mbuti Pygmy (red) and "B" = Bushmen (blue); followed by a shortened label; then, Q16 (29), for example, which indicates a quadruple-pulse timeline with 16 pulse per cycle followed a number identifier in brackets from Table 1. The distances between nodes when travelling along the lengths of the branches are proportional to the distances between the corresponding patterns in the matrix (Dress et al., 1996). A high LSfit measure of 99.8% indicates that the trees faithfully represent the distance matrix.
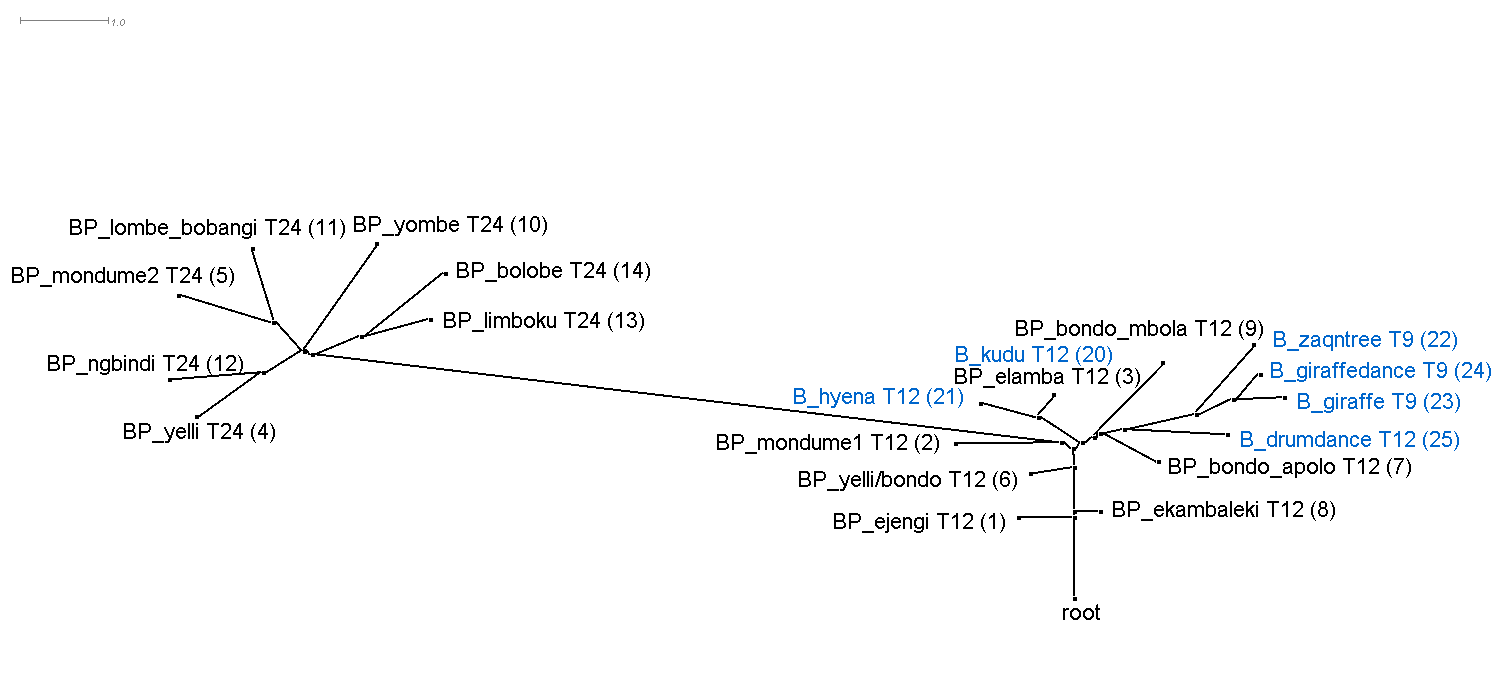
Figure 4b. Rooted phylogenetic tree of the triple-pulse timelines from Table 1. "BP" = BaYaka Pygmy (black) and "B" = Bushmen (blue). LSfit = 99.45%.
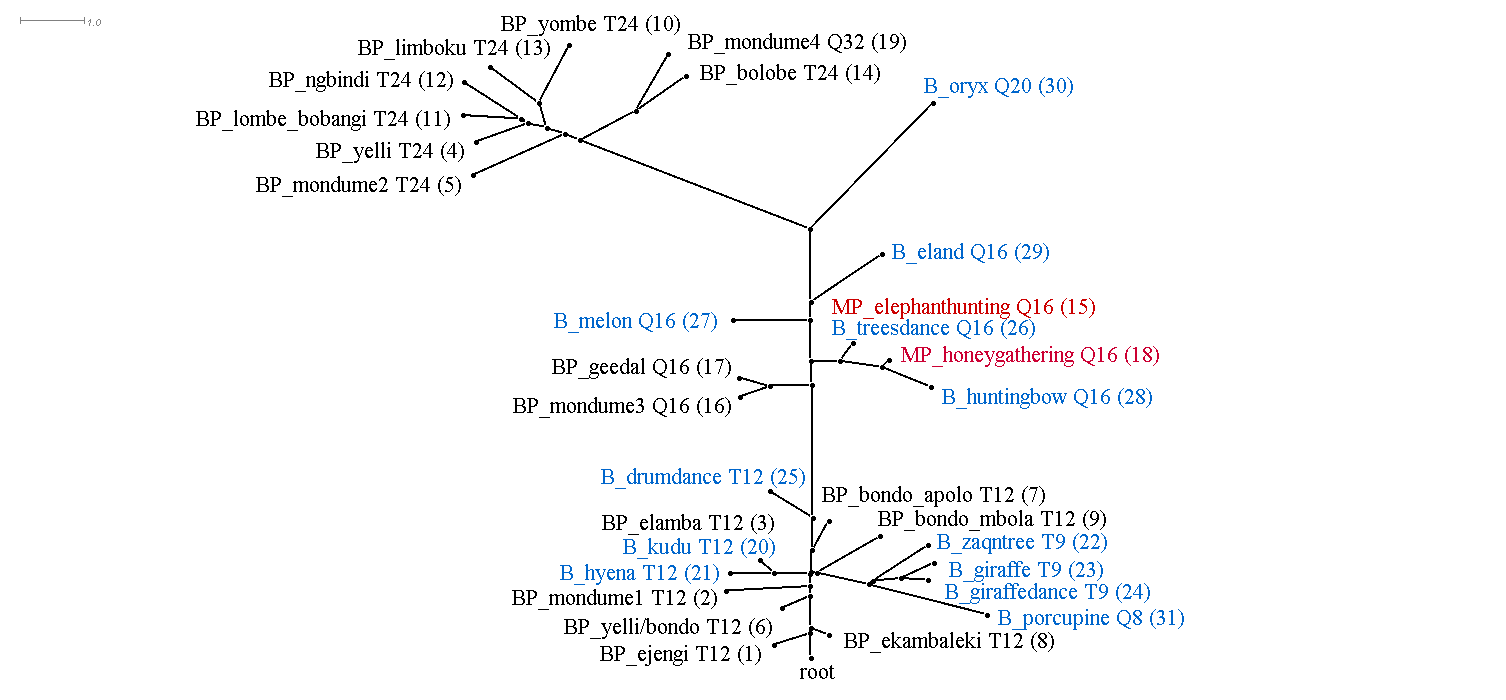
Figure 4c. Rooted phylogenetic tree of all triple-pulse and quadruple-pulse timelines from Table 1. "BP" = BaYaka Pygmy (black), "MP" = Mbuti Pygmy (red) and "B" = Bushmen (blue). LSfit = 99.06%.
Figure 4a-c shows that one of the main distinguishing features that has influenced the cluster relationships in the phylogenetic trees is pattern length or number of pulses per cycle. This is most evident in Figures 4b and 4c. In Figure 4b, the cluster that branches off to the left of the tree contains 24-pulse timelines, the centre of the tree contains 12-pulse timelines, and the cluster to the right contains mainly 9-pulse timelines. Similarly, in Figure 4c, longer 32-pulse and 24-pulse timelines feature in the left-hand branch of the tree, 16-pulse timelines occupy the middle of the tree, and shorter 12-pulse and 9-pulse timelines are found towards the root of the tree.
This clustering makes sense because the edit-distance algorithm used to generate the distance matrix would require a greater number of edits to transform, for example, a 12-pulse timeline to a 24-pulse timeline than timelines of the same length. However, before dismissing the edit-distance algorithm as perhaps too general for fine-grained comparative study, it is worth noting that the distances calculated also depend on the placement of strokes within each timeline being compared as well as the pattern length. Future research, therefore, might use phylogenetic analysis to compare timelines of the same length in order to identify the hierarchical relationships between them and to identify common structural features.
The main goal here however is to identify ancestral rhythms. Each of the trees in Figure 4 show a node labelled 'root' at the bottom of the graph, indicating that the most recent common ancestor is unknown and that there is no clear ancestral timeline rhythm.
Population geneticists have also used phylogenetic models to understand our common ancestry and they provide some important insights. Starting in the 1960s with the work of Cavalli-Sforza and his associates, a body of research has been amassed that has furthered the understanding of worldwide biological diversity patterns and human origins and migrations by analysing the structure of human DNA. The most up-to-date model to emerge from this research (Cavalli-Sforza et al., 1994) suggests that "the current peopling of the world results from serial migrations "Out of Africa" over the past 100,000 years. In this model, mankind expanded throughout the world via a series of migrations increasingly distant from the African source, each migration followed by founding events of new populations" (Verdu, 2014, p. 33). In his review of this body of research, Paul Verdu (2014) concludes that, although the findings are still open to debate, there is an ancient common origin between central African Pygmy and non-Pygmy populations dating to around 70,000 years ago and a likely common origin between Eastern and Western Pygmy groups dating to roughly 20,000 years ago (p. 45).
Drawing on the 'Out-of-Africa' model (Cavalli-Sforza et al., 1994; Chen et al., 2000; Oppenheimer, 2012), as well as studies in archaeology, ethnomusicology, anthropology, linguistics, and his work with Alan Lomax on the Cantometric project, Victor Grauer (2011) argues that eastern Pygmy, western Pygmy, and Bushmen cultural practices are derived from a "Hypothetical Baseline Culture," which represents the core values of a common ancestral group (p. 3) 10. The location of this ancestral group is "unknown" but is possibly the "tropical forest or East African savannah" (p. 57). Fascinatingly, the music, Grauer writes, may have survived from the historical 'moment' when these cultural groups diverged somewhere between 70,000 and 100,000 years ago:
Astonishing as it might sound, by listening to a recording of traditional Pygmy or Bushmen music, we are, in a sense, entering a kind of time warp, hearing the sorts of sounds our African ancestors may well have been making anywhere from 70,000 to over 100,000 years ago (p. 2).
Grauer's emphasis, like many Pygmy/Bushmen comparative studies, is the similarities in song/singing style (vocal polyphony, counterpoint, and yodelling) and not timelines. As Grauer acknowledges, there are also alternative hypotheses that could explain the diffusion of musical elements over a geographical area: independent invention (coincidence) and convergent evolution, "based on the assumption that the tradition represents an adaptation of some sort, stemming from some universal property of the human mind" (p. 72). Nonetheless, his theory is an intriguing one that might explain the timeline data presented above.
It is conceivable that foundational rhythms such as the 3:2 pattern featured in the music of a common ancestral group and the timelines in Table 1 are later adaptations that build on and extend this basic structural theme. If the location of this ancestral group was somewhere in east Africa, as some genetic studies suggest (Cavalli-Sforza & Feldman, 2003), perhaps rhythms containing the 3:2 pattern migrated westwards and southwards from this location and were subsequently adapted by Pygmy and Bushmen groups into the timelines seen in Table 1. Pushing the speculation further, perhaps the widely-used "standard patterns" (2212221, 22323, 33424) found in Pygmy music are later adaptations that migrated to other parts of sub-Saharan Africa and then 'out of Africa' through cultural interactions with their non-Pygmy neighbours.
These are interesting issues to explore but extreme caution is required when reconstructing complex cultural practices such as music that may originate far back in the Paleolithic era. The first problem is the huge time spans in question, since solid documentary evidence of the music played by Pygmy and Bushmen dates from only around 70-100 years ago. We know absolutely nothing of the rhythms played by these cultural groups dating from 70,000-100,000 years ago and how and why they may have developed and mutated since then.
A second problem is that the hypothesis outlined here relies heavily on data from genetic research. Therefore, it is built on the notion that there is a strong correlation between biological evolution and ancestry, and cultural (Mace et al., 2005) and musical evolution (Nettl, 2006). This correlation may exist. Brown et al. (2014) examined the statistical correlations between music, language and genes among nine indigenous populations of Taiwan using "traditional group-level folk songs and mitochondrial DNA" (p. 1). They conclude that "the correlation between music and genes was statistically significant" and that "music – particularly polyphonic group singing – might serve as a useful marker to study human migrations and human origins more generally" (p. 4). In a related study, Rzeszutek et al. (2012) argue that "many useful parallels have been drawn between cultural and biological evolution", but add that "the forces shaping cultural diversity can differ markedly from those that drive the structure of genetic diversity" (p. 1611). A similar note of caution is provided by Savage and Brown (2013). They point out that "it is crucial to remember that music evolution does not necessarily mirror the patterns of language, genes, or any other system" (p. 9). The precise relationship between Pygmy/Bushmen biological and musical evolution remains unknown.
A third, related problem is that "the study of ancient DNA has been extremely contentious" (Olson, 2002, p. 80) and that in the equatorial forests of the Congo Basin, where the majority of Pygmy groups have always lived, the soil is acidic and rapidly decays human bones (Cavalli-Sforza et al., 1994, pp. 160, 180). "Even when fossils between 15,000 and 150,000 years old have been found, linking the bones with existing groups has proved difficult" (Olson, 2002, p. 50). As a result, "biological anthropologists are challenged by a tremendous lack of historical and demographic knowledge, even recent, in central Africa" (Verdu, 2014, pp. 34-35).
Clearly, further study is needed to reliably reconstruct the musical practices of sub-Saharan Africa's ancient (and more recent) past. If indeed such a reconstruction is possible, the data presented above indicates that the comparative study of resilient and foundational musical features, such as timelines, has much to offer such an endeavour.
CONCLUSIONS
In this article, I have used theories of African rhythm from ethno/musicology, findings from anthropological research and population genetics, musical analyses based on transcriptions, and computational phylogenetic techniques to compare the intervallic, cyclical, and structural properties of 31 timeline rhythms performed in Pygmy and Bushmen musical cultures. By utilising these different analytical and theoretical perspectives, some interesting similarities and differences have been brought to light.
Despite variations in cycle length and the number and placement of strokes, Pygmy and Bushmen timelines are highly interrelated. The 'rhythmic oddity' model is useful is explaining the structural connections between timelines used by Pygmy groups from the Western-Central Africa; a generative approach highlights how many Pygmy/Bushmen and African and African-derived timelines feature commonly used rhythmic cells, such as the 3:2 pattern that form their structural and aesthetic bases; and the principle of maximal evenness suggests that Pygmy/Bushmen groups show a preference for timelines that are regular and almost regular. Furthermore, these models highlight important relationships between some Pygmy/Bushmen timelines, especially the well-known "standard patterns," and those used in music in other parts of sub-Saharan Africa, the Caribbean, and beyond that could be explored in future studies.
The accompanying ethnographic data suggests that timelines are multi-purpose musical devices used in various different types of events and social contexts both within and across Pygmy and Bushmen cultures. Moreover, the foundational structure of timelines appear to be resilient to radical change, their basic structure remaining unaltered in old and new musical forms and cultural settings.
Phylogenetic analysis of the 31 timelines revealed that pattern length and the number and placement of the strokes are the factors influencing cluster relationships. Phylogenetics also reveal that no clear Pygmy/Bushmen ancestral timeline comes to the fore.
Future research is needed to shed more light on Africa's complex cultural and musical history, and to formulate a more coherent theory of musical evolution and its relationship to biological evolution. The approach used recently by Brown et al. (2014), which examines the coevolutionary relationships between musical, genetic, linguistic, and geographic distances, is an important step forward but could be expanded to include detailed ethnomusicological research on the structure of the foundational rhythmic features that underpin music making in sub-Saharan Africa. Future studies that aim to map and quantify the generative adaptations of rhythms within Pygmy and Bushmen societies over a period of time, and how they may have changed on their journey to places like Cuba would also provide useful insights into the processes that drive musical evolution. I hope that the current study has shown that timelines are a productive resource in the quest to uncover Africa's intriguing musical history, development, and influence.
ACKNOWLEDGEMENTS
I am very grateful to Jerome Lewis and Martin Clayton for critical readings on earlier drafts of this paper, and to reviewers Justin London and Victor Grauer for their extremely helpful comments. Thank you to Kit Opie for his insights into phylogenetic analysis and for supplying numerous references. Thank you also to Camille Oloa-Biloa for kindly supplying and contextualising her Mbendjele field recordings. This project was funded by the Leverhulme Trust grant RP2011-R-045. This article was copyedited by Dana Lauren DeVlieger and layout edited by Kelly Jakubowski.
NOTES
-
Correspondence can be addressed to: Adrian Poole, UCL Anthropology, 14 Taviton Street, London WC1H 0BW. E-mail: adrian.poole@ucl.ac.uk.
Return to Text -
According to Kofi Agawu (2006, p. 3), the term "time line" was first used by Ghanaian music scholar Kwabena Nketia in 1963 (Nketia, 1963, p. 78). Agawu's paper also provides a useful summary of the debate surrounding the precise meaning and usage of the term. It is used throughout the current study to refer to particular, continually repeated rhythms that mark the fundamental cyclical structure of Pygmy/Bushmen music (performed with metal blades, sticks, drums, or handclaps), and rhythms that play the same role in many African and African-related music (typically played on an iron bell in many West African musical cultures and wooden 'clave' in Afro-Cuban music (Toussaint, 2013, pp. 17-21).
Return to Text -
See Toussaint (2013) for a list of references.
Return to Text -
See Appendix A for a list of timelines, performance tempi, sources, dates and other details. Available at: http://hdl.handle.net/1811/85870.
Return to Text -
TUBS, also known as Box Notation Method, has become popular with ethnomusicologists and percussionists as an alternative to Western notation. Using marks in boxes to indicate where percussive strokes occur in time, it offers a simple method of notating musical rhythm and showing relationships between them (Arom, 1991; Kaufman Shelemay, 2000; Koetting, 1970; Ekwueme, 1974).
Return to Text -
See Toussaint (2004) and Lui and Toussaint (2010) for uses of these notational systems in various domains and associated references.
Return to Text -
See also London (2004) and Taylor (2012) for further comparative applications of Arom's theory and Chemiller and Truchet's (2003) article on the relationship between Lyndon words and the rhythmic oddity property.
Return to Text -
See also Toussaint (2010).
Return to Text -
See Olivier & Fürniss (1999) for more detail on categories in Aka Pygmy and Ju'hoansi Bushmen music.
Return to Text -
See also Grauer (2006, 2009) and Lomax (1976, 1968) on Cantometrics. For a contrasting viewpoint see Olivier and Fürniss (1999), Leroi and Swire (2006), Nettl (2006), and Stock (2006) for a critic of Grauer's theory.
Return to Text
REFERENCES
- Agawu, K. (1995). African rhythm: A Northern ewe perspective. Cambridge: Cambridge University Press.
- Agawu, K. (2006). Structural analysis or cultural analysis? Competing perspectives on the "standard pattern" of West African rhythm. Journal of the American Musicological Society, 59(1), 1-46. https://doi.org/10.1525/jams.2006.59.1.1
- Ahmadzadeh, R. (2012). Edit Distance Algorithm. Retrieved from http://uk.mathworks.com/matlabcentral/fileexchange/39049-editdistancealgorithm/content/EditDistance.m
- Anku, W. (2000). Circles and time: A theory of structural organization of rhythm in African music. Music Theory Online, 6(1).
- Arom, S. (1989). Time structure in the music of central Africa: Periodicity, meter, rhythm and polyrhythmics. Leonardo, 22(1), 91-99. https://doi.org/10.2307/1575146
- Arom, S. (1991). African polyphony and polyrhythm. Cambridge: Cambridge University Press. https://doi.org/10.1017/CBO9780511518317
- Bleek, D. F. (1928). The Naron: A Bushman tribe of the Central Kalahari. Cambridge: Cambridge University Press.
- Brearley, J. (1982). Group of Bushmen, singing and dancing. Mongongo (nut) tree. Retrieved from http://sounds.bl.uk/World-and-traditional-music/John-Brearley-Botswana/025M-C0065X0003XX-1800V0
- Brown, S., Savage, P. E., Ko, A. M.-S., Stoneking, M., Ko, Y.-C., Loo, J.-H., & Trejaut, J. A. (2014). Correlations in the population structure of music, genes and language. Proceedings of The Royal Society B: Biological Sciences, 281, 1-7.
- Cavalli-Sforza, L. L., & Feldman, M. W. (2003). The application of molecular genetic approaches to the study of human evolution. Nature Genetics Supplement, 33, 266-275. https://doi.org/10.1038/ng1113
- Cavalli-Sforza, L. L., Menozzi, P., & Piazza, A. (1994). The history and geography of human genes. Princeton: Princeton University Press.
- Chemillier, M., & Truchet, C. (2003). Computation of words satisfying the "rhythmic oddity" property (after Simha Arom's work). Information Processing Letters, 86, 255-261. https://doi.org/10.1016/S0020-0190(02)00521-5
- Chen, Y.-S., Olckers, A., Schurr, T. G., Kogelnik, A. M., Huoponen, K., & Wallace, D. C. (2000). mtDNA variation in the South African Kung and Khwe—and their genetic relationships to other African populations. American Journal of Human Genetics, 66(4), 1362–1383. https://doi.org/10.1086/302848
- Chernoff, J. M. (1991). The rhythmic medium in African music. New Literary History, 22(4), 1093-1102. https://doi.org/10.2307/469080
- Clough, J., & Douthett, J. (1991). Maximally even sets. Journal of Music Theory, 35, 93-173. https://doi.org/10.2307/843811
- Dress, A., Huson, D., & Moulton, V. (1996). Analyzing and visualizing sequence and distance data using SplitsTree. Discrete Applied Mathematics, 71(1), 95-109. https://doi.org/10.1016/S0166-218X(96)00059-5
- Ekwueme, L. (1974). Concepts in African musical theory. Journal of Black Studies, 5(1), 35–64. https://doi.org/10.1177/002193477400500103
- England, N. (1967). Bushman counterpoint. Journal of the International Folk Music Council, 19, 58-66. https://doi.org/10.2307/942188
- England, N. (1995). Music among the ʒũ’|’wã-si and related peoples of Namibia, Botswana, and Angola. New York: Garland Publishing.
- Frisbie, C. J. (1971). Anthropological and ethnomusicological implications of a comparative analysis of Bushmen and African Pygmy music. Ethnology, 10(3), 265-290. https://doi.org/10.2307/3772917
- Fürniss, S. (2006). Aka polyphony: Music, theory, back and forth. In M. Tenzer (Ed.), Analytical Studies in World Music (pp. 163-204). Oxford: Oxford University Press. https://doi.org/10.1093/acprof:oso/9780195177893.003.0006
- Fürniss, S. (2014). Diversity in Pygmy music: A family portrait. In B. S. Hewlett (Ed.), Hunter gatherers of the Congo Basin: Cultures, histories and biology of African Pygmies (pp. 187-218). New Brunswick: Transaction Publishers.
- Fürniss, S., & Joiris, D. V. (2011). A dynamic culture: Ritual and musical creation in the Baka context. Before Farming, 4(3), 1-12. https://doi.org/10.3828/bfarm.2011.4.3
- Garca, S. d., & Tehrani, J. J. (2016). Comparative phylogenetic analyses uncover the ancient roots of Indo-European folktales. Royal Society Open Science, 3, 1-11.
- Gascuel, O. (1997). BIONJ: An improved version of the NJ algorithm based on a simple model of sequence data. Molecular Biology and Evolution, 14(7), 685-695. https://doi.org/10.1093/oxfordjournals.molbev.a025808
- Grauer, V. (2006). Echoes of our forgotten ancestors. The World of Music, 48(2), 5-58.
- Grauer, V. (2009). Concept, style, and structure in the music of the African Pygmies and Bushmen: A study in cross-cultural analysis. Ethnomusicology, 53(3), 396-424.
- Grauer, V. (2011). Sounding the depths: Tradition and the voices of history. CreateSpace.
- Grimaud, Y., & Rouget, G. (1956). Notes on the music of the Bushmen compared to that of the Babinga Pygmies (notes for a long-playing record): Cambridge, Massachusetts: Peabody Museum and Paris: Musée de l'Homme.
- Guastavino, C., Gόmez, F., Toussaint, G., Marandola, F., & Gόmez, E. (2009). Measuring similarity between Flamenco rhythmic patterns. Journal of New Music Research, 38(2), 129-138. https://doi.org/10.1080/09298210903229968
- Hewlett, B. S. (Ed.) (2014). Hunter-Gatherers of the Congo Basin: Cultures, histories and biology of African Pygmies. New Brunswick: Transaction Publishers.
- Huson, D. H. (1998). SplitsTree: Analyzing and visualizing evolutionary data. Bioinformatics, 14(1), 68-73. https://doi.org/10.1093/bioinformatics/14.1.68
- Huson, D. H., & Bryant, D. (2006). Application of phylogenetic networks in evolutionary studies. Molecular Biology and Evolution, 23(2), 254–267. https://doi.org/10.1093/molbev/msj030
- Jones, A. M. (1959). Studies in African music Vol 1. London: Oxford University Press.
- Katz, R., Biesele, M., & Shostak, M. (1982). Healing dance music of the Kalahari San (notes for CD): Ethnic Folkways Records FE 4316.
- Kaufman Shelemay, K. (2000). Notation and oral tradition. In R. Stone (Ed.), The Garland handbook of African music (pp. 24-42). New York: Taylor & Francis.
- King, A. (1960). Employments of the "standard pattern" in Yoruba music. African Music, 2(3), 51-54. https://doi.org/10.21504/amj.v2i3.610
- Kisliuk, M. (1998). Seize the dance: BaAka musical life and the ethnography of performance. New York: Oxford University Press.
- Koetting, J. (1970). Analysis and notation of West African drum ensemble music. Publications of the Institute of Ethnomusicology, 1(3), 116-146.
- Kubik, G. (1999). Africa and the blues. Jackson: University Press of Mississippi.
- Kubik, G. (2010). Theory of African music Vol 1 and 2. Chicago: Chicago University Press. https://doi.org/10.7208/chicago/9780226456928.001.0001
- Lee, R. B., & Daly, R. (1999). The Cambridge encyclopedia of hunters and gatherers. Cambridge: Cambridge University Press.
- Leroi, A. M., & Swire, J. (2006). The recovery of the past. The World of Music, 48(2), 43–54.
- Levenshtein, V. I. (1966). Binary codes capable of correcting deletions, insertions, and reversals. Soviet Physics-Doklady, 10(8), 707–710.
- Lewis, J. (2002). Forest hunter-gatherers and their world: A study of Mbendjele Yaka Pygmies of Congo-Brazzille and their secular and religious activities and representations. Unpublished doctoral diss., London School of Economics and Political Science, United Kingdom.
- Lewis, J. (2013). A cross-cultural perspective on the significance of music and dance to culture and society: Insight from BaYaka Pygmies. In M. A. Arbib (Ed.), Language, music, and the brain (pp. 45-65). Cambridge, MA: MIT Press. https://doi.org/10.7551/mitpress/9780262018104.003.0002
- Lewis, J. (2014). Egalitarian social organisation: The case of the Mbendjele BaYaka. In B. S. Hewlett (Ed.), Hunter-gatherers of the Congo Basin: Cultures, histories and biology of African Pygmies (pp. 219-243). New Brunswick: Transaction Publishers.
- Liu, Y., & Toussaint, G. T. (2010). Mathematical notation, representation, and visualization of musical rhythm: A comparative perspective, Proceedings of the International Conference on Computer and Computational Intelligence, Nanning, China, December 25-26, 2010, Vol. 1, pp. 28-32.
- Locke, D. (1996). Africa: Ewe, Mande, Dagbamba, Shona, BaAka. In J. T. Titon (Ed.), Worlds of music: An introduction to the music of the world's peoples (pp. 78-101). London: Prentice Hall.
- Locke, D. (1998). Drum Gahu: An introduction to African rhythm. Tempe, Arizona: Whitecliff Media.
- Lomax, A. (1962). Song structure and social structure. Ethnology, 1(4), 425-451. https://doi.org/10.2307/3772850
- Lomax, A. (1968). Folk song style and culture. Washington, D.C.: American Association for the Advancement of Science.
- Lomax, A. (1976). Cantometrics: An approach to the anthropology of music. Berkeley: University of California Extension Media Center.
- London, J. (2004). Hearing in time: Psychological aspects of musical meter. New York: Oxford University Press. https://doi.org/10.1093/acprof:oso/9780195160819.001.0001
- Mace, R., Holden, C. J., & Shennan, S. (Eds.). (2005). The evolution of cultural diversity: A phylogenetic approach. London: UCL Press.
- Marshall, L. (1976). The !Kung of Nyae Nyae. Cambridge, Massachusetts: Harvard University Press. https://doi.org/10.4159/harvard.9780674180574
- Nettl, B. (2006). Response to Victor Grauer: On the concept of evolution in the history of ethnomusicology. The World of Music, 48(2), 59-72.
- Nketia, K. J. H. (1963). African music in Ghana. Evanston, Illinois: Northwestern University Press.
- Novotney, E. D. (1998). The 3:2 relationship as the foundation of timelines in West African musics. Unpublished doctoral thesis, University of Illinois at Urbana-Champaign.
- Olivero, J., Fa, J. E., Farfán, M. A., Lewis, J., Hewlett, B., Breuer, T., … Nasi, R. (2016). Distribution and numbers of Pygmies in Central African forests. PLoS ONE, 11(1), e0144499. https://doi.org/10.1371/journal.pone.0144499
- Olivier, E. (1998). Bushmen vocal music: The illusion of polyphony. In M. Schladt (Ed.), Language, identity, and conceptualization among Khoisan (pp. 359-370). Cologne: Rüdiger KöppeVerlag.
- Olivier, E. (2001). Categorizing the Ju'hoan musical heritage. African Study Monographs, 27, 11-27.
- Olivier, E., & Fürniss, S. (1999). Pygmy and Bushman music: A new comparative study. In K. Biesbrouck, S. Elders, & G. Rossel (Eds.), Central African hunter gatherers in a multidisciplinary perspective: Challenging elusiveness (pp. 117-132). Leiden: Research School for Asian, African, and Amerindian Studies.
- Olson, S. (2002). Mapping human history: Discovering the past through our genes. London: Bloomsbury.
- Oppenheimer, S. (2012). Out-of-Africa, the peopling of continents and islands: Tracing uniparental gene trees across the map. Philosophical Transactions of Royal Society B, 367, 770-784. https://doi.org/10.1098/rstb.2011.0306
- Peñalosa, D. (2009). The Clave matrix. Afro-Cuban rhythm: Its principles and African origins. California: Bembe Books.
- Post, O., & Toussaint, G. T. (2011). The edit distance as a measure of perceived rhythmic similarity. Empirical Musicology Review, 6(3), 164-179. https://doi.org/10.18061/1811/52811
- Pressing, J. (1983). Cognitive isomorphisms between pitch and rhythm in world music: West Africa, the Balkans and Western tonality. Studies in Music, 17, 38-61.
- Rahn, J. (1996). Turning the analysis around: Africa-derived rhythms and Europe-derived theory. Black Music Research Journal, 16(1), 71-89. https://doi.org/10.2307/779378
- Rzeszutek, T., Savage, P. E., & Brown, S. (2012). The structure of cross-cultural musical diversity. Proceedings of The Royal Society B: Biological Sciences, 279, 1606-1612. https://doi.org/10.1098/rspb.2011.1750
- Sarno, L. (1993). Song from the forest: My life among the Ba-Benjellé Pygmies. London: Bantam Press.
- Sarno, L. (1995). Bayaka: The extraordinary music of the Babenzele Pygmies and sounds of their forest home. Roslyn, New York.: Ellipsis Arts.
- Sarno, L. (2016). BayAka women singing Limboku songs. Retrieved from https://soundcloud.com/noel-lobley/sets/louis-sarno-bayaka-recordings
- Savage, P. E., & Brown, S. (2013). Toward a new comparative musicology. Analytical Approaches To World Music, 2(2), 148-197.
- Stock, J. P. J. (2006). Clues from our present peers? A Response to Victor Grauer. The World of Music, 48(2), 73-91.
- Taylor, S. A. (2012). Hemiola, maximal evenness, and metric ambiguity in late Ligeti. Contemporary Music Review, 31(2-3), 203-220. https://doi.org/10.1080/07494467.2012.717362
- Tehrani, J., & Collard, M. (2002). Investigating cultural evolution through biological phylogenetic analyses of Turkmen textiles. Journal of Anthropological Archaeology, 21(4), 443-463. https://doi.org/10.1016/S0278-4165(02)00002-8
- Toussaint, G. T. (2003). Classification and phylogenetic analysis of African ternary rhythm timelines. BRIDGES: Mathematical Connections in Art, Music, and Science, University of Granada, Spain, July 23-27, 2003, pp. 25-36.
- Toussaint, G. T. (2004). A comparison of rhythmic similarity measures. 5th International Conference on Music Information Retrieval, Barcelona, Spain, 2004, pp. 242-245.
- Toussaint, G. T. (2010). Generating "good" musical rhythms algorithmically. 8th International Conference on Arts and Humanities, Honolulu, Hawaii, January 13-16., 2010, pp. 774-791.
- Toussaint, G. T. (2013). The geometry of musical rhythm. Boca Raton, Florida: CRC Press.
- Toussaint, G. T., Campbell, M., & Brown, N. (2011). Computational models of symbolic rhythm similarity: Correlation with human judgments. Analytical Approaches To World Music, 1(2), 380-430.
- Toussaint, G. T., Matthews, L., Campbell, M., & Brown, N. (2012). Measuring musical rhythm similarity: Transformation versus feature-based methods. Journal of Interdisciplinary Music Studies, 6(1), 23-53.
- Turnbull, C. (1961). Music of the rain forest Pygmies: The historic recordings made by Colin M. Turnbull (notes for CD): LYRCD 7157.
- Turnbull, C. (1965). Waywood servants: The two worlds of the African Pygmies. New York: The Natural History Press.
- Verdu, P. (2014). Population genetics of Central African Pygmies and Non-Pygmies. In B. S. Hewlett (Ed.), Hunter-gatherers of the Congo Basin: Cultures, histories and biology of African Pygmies (pp. 31-58). New Brunswick, New Jersey: Transaction Publishers.
- Walker, R., Hill, K. R., Flinn, M. V., & Ellsworth, R. M. (2011). Evolutionary history of hunter gatherer marriage practices. PLoS ONE, 6(4), 1-6. https://doi.org/10.1371/journal.pone.0019066
DISCOGRAPHY
- Apelian, N. (2015). Nharo Bushmen Hyena Song with Musical Bow. Retrieved from https://www.youtube.com/watch?v=yktziU75QI0
- Arom, S. (2003). Central Africa: Musical anthology of the Aka Pygmies: OCORA 560171/72 CD.
- Baka.co.uk. (2016). The Baka forest people. Retrieved from http://www.baka.co.uk/baka/
- Brearley, J. (1982). John Brearley collection (C65). Retrieved from http://sounds.bl.uk/World-and-traditional-music/John-Brearley-Botswana
- Kisliuk, M. (1998). Seize the dance. Retrieved from http://global.oup.com/us/companion.websites/0195308697/kisliuk/downloads/
- Olivier, E. (1997). Namibia: Chants des Bushmen Ju'hoansi (Songs of the Ju'Hoansi Bushmen). France: Ocora 560117 CD.
- Olivier, E. (2003). Bushmen Ju'hoansi: Instrumental music. France: Ocora C 560179 CD.
- Oloa-Biloa, C. (2013/2014). Unpublished audio and video Recordings of Mbendjele music.
- Phillipson, J. (1962). Music of !Kung Bushmen of the Kalahari desert, Africa. New York: Ethnic Folkways, FE 4487 CD.
- Rouget, G. (1948). Recordings of Pygmy Music from the 1946 Ogooué-Congo Mission. Retrieved from http://publicdomainreview.org/collections/recordings-of-pygmy-music-from-the-1946-ogooue-congo-mission/
- Rouget, G. (2014). Musique Pygmée de la Haute-Sangha (Mono Version). France: BNF Collection CD.
- Rouget, G., & Grimaud, Y. (1956). Bushman music and Pygmy music: Cambridge, Massachusetts: Peabody Museum and Paris: Musée de l'Homme CD.
- Sarno, L. (1987). Louis Sarno archive at the Pitt Rivers museum. Retrieved from https://soundcloud.com/noel-lobley/sets/louis-sarno-bayaka-recordings
- Sarno, L. (1995). Bayaka: The extraordinary music of the Babenzele Pygmies and sounds of their forest home. Roslyn, N.Y.: Ellipsis Arts 3490 CD.
- Shostak, M., Biesele, M., Marshall, J., England, N., & Katz, R. (2005). Music of the Kalahari San: Instrumental pieces and songs of the healing dance. South Africa: Kalahari Peoples Fund CD.
- Turnbull, C. (1993). Music of the rainforest Pygmies. The historical recordings made by Colin M. Turnbull. New York: Lyrichord 7157 CD.


