Computational analysis of large data sets has transformed many aspects of academic inquiry, allowing scholars to quantify historical trends and bolster intuitive observations with large amounts of evidence. As the fields of music theory and musicology experiment with such methods, there arises a need for large data sets, for example, the Million Song Dataset (Bertin-Mahieux, Ellis, Whitman, & Lamere 2011) as well as computational tools as the music21 library (Cuthbert & Ariza 2011). However, the technology for symbolic transcription of audio data is not yet sufficiently developed to render corpora of audio files accessible to pitch- or harmonic-based music theoretical inquiry. Several music theorists have created their own corpora of musical scores, either collecting chord annotations (Burgoyne, Wild, & Fujinaga 2013, deClercq & Temperley 2011) or symbolic digital representations of the scores themselves (Temperley 2009, Duane 2012); however, these corpora are often limited in scope, frequently because they rely on a small group of researchers to manually encode the pitches and rhythms of each piece.
In an attempt to fill this gap and provide music researchers with a large dataset of symbolic musical data, The Yale-Classical Archives Corpus (YCAC) categorizes and pre-processes the trove of MIDI files available at classicalarchives.com, tagging each file with useful metadata. This paper introduces the corpus by describing the processes used in compiling and tagging the raw data, and by summarizing some properties of the corpus.
Classicalarchives.com bills itself as "the largest classical music site on the web." 2 The site began in 1994 as a forum for user-uploaded MIDI files, before expanding to a subscription service, first to provide access to the site's MIDI files, and then to its collection of MP3s. In 2010, the Yale Department of Music was granted unlimited access to a 1999 version of website in order to download the embedded MIDI files for research purposes. In this version, the site's MIDI files are divided by composer and then grouped under several headings corresponding to the classification used by classicalarchives.com: the composers with the largest number of uploads comprise "The Greats;" pre-1600 composers are grouped in "Early Music;" and the remaining composers are grouped according to the first letter of their last names. The MIDI files are additionally labeled with the user who uploaded the file, if known. The method of encoding varies, with some users translating the file from another symbolic encoding (e.g., into a music notation program such as Finale or Kern) and other users uploading their MIDI-keyboard performances. 3
Metadata
Each piece in the YCAC is associated with a variety of fields that might be appropriate for musicological research. Title records the name of the piece as listed on classicalarchives.com. Composer is the last name of the composer as spelled in Grove Music Online, a standard reference work. CatNo identifies the piece within a composer's output, using a standard catalog number (e.g. BWV, Köchel, or opus number), and is left blank in the absence of a standard catalog. Date is the year of first publication in the composer's lifetime, or the year of composition for unpublished works. A range of possible dates is given if no precise year is known; for certain anonymous compositions this field is left blank. Instrumentation is a delimited list of instruments in the case of solo or chamber pieces, or the name of the ensemble in the case of works for larger groups. Genre indicates the piece's compositional or formal type: examples of genres include "symphony," "character piece," "opera," or "mass." The genre can be further specified by indicating its Species, noting, say, that a piece is a slow movement of a symphony, a recitative of an opera, or a Credo of a mass. While each piece has a genre, not every genre divides into species. For instance, the genre "character piece" would not necessarily require further specification. Nationality is taken, whenever possible, from the first word of the composer's biography in Grove Music Online. If the online entries or the piece's title referenced the music's key, that was given as the file's OpeningKey. (e.g., "Sonata in C major" would be recorded as C major.) Otherwise, the research assistants were instructed to use their musical judgment to determine the prevailing key of the opening eight measures; the final eight measures were also played to determine whether the piece modulates (ClosingKey). Picardy thirds at the end of minor-key pieces were thus not recorded as major-key endings.
Metadata were compiled by student research assistants enrolled either as graduate students in the Yale Department of Music or as undergraduates in Yale College. The procedure was as follows. First, they downloaded the MIDI file for a particular piece and opened it in music notation software, either Sibelius or Finale. In cases where there was more than one uploaded file for a piece, they were instructed to choose the simplest and cleanest encoding (i.e., with less rubato, fewer velocity changes, etc.). If a file included more than one movement of a multi-movement work, they were instructed to divide the file into its constituent parts. The piece's catalogue number, date, genre/species, and nationality were found by referencing online resources such as Grove Music Online and IMSLP.org.
While listening and scanning the notation file, the research assistants were also instructed to delete any obvious mistakes within the encoding; if the mistakes were overwhelming, the file was not included in the corpus. (For instance, several files included pitch events that had onset cues, but no offset cues, which would therefore sound for the remainder of the piece. If these mistakes could be fixed, they would be; if they were pervasive throughout the file, the file was thrown out.) The notation file was then exported as a MIDI file, using a handle that associated the MIDI file with the metadata.
Representing the Corpus
Since MIDI files themselves can be cumbersome to convert into other representations for use within a data analysis, we processed the files in a manner that would standardize the piece's pitch information and make it easily accessible for modeling and analysis. Using the music21 software package's chordify() function, we "salami sliced" the files into verticalities each time a pitch was added or subtracted from the texture. 4 Each slice is represented as a record within a CSV file. Data fields for each slice include the filename of the source MIDI file, the offset in quarter notes from the beginning of the piece, several representations of the slice's pitch content, and information about the local key context. The pitch content of each slice is represented in five different ways. The first four are as follows:
- RawPitchTuple: A list of MIDI numbers corresponding to pitches in the slice, separated by commas and surrounded by square brackets.
- NormalForm: A set of integers modulo 12, separated by commas and surrounded by square brackets, representing the set-class of the chord up to transposition (but not inversion). The normal-form representation is determined by the chord.normalForm() function in music21. For example, any major triad will have the normal form [0, 4, 7], and any dominant-seventh chord will have the normal form [0, 3, 6, 8].
- PCNormalOrder: An element-wise transposition of NormalForm such that each pitch-class in the slice (MIDI number modulo 12) is included in the set. For example, an E dominant-seventh chord will be notated as [8, 11, 2, 4], an element-wise transposition of [0, 3, 6, 8] by the appropriate interval.
- GlobalSDNormalOrder: An element-wise transposition of PCNormalOrder by the interval required to normalize the key of the piece to C major or minor. For example, for a piece in A major, an E dominant-seventh chord will be notated as [11, 2, 5, 7], corresponding to the notes of the G dominant seventh chord that would result from transposing the piece up a minor third from A major to C major.
The last representation, which normalizes pitch-class content by the global key of each piece (thus transforming pitch-classes into scale degrees relative to the global tonic) is of limited use, especially in longer pieces with many modulations. We therefore subjected each piece to a windowed key-finding process. At each salami-slice's time point, the process compiles a window of the durations of each pitch class between that slice's time point and the time point eight quarter notes in the future. This window is analyzed by a key-profile analysis, specifically the music21 Bellman-Budge function (Bellman 2005). (In this type of automated key-finding, the algorithm compares the number of times each pitch-class occurs in the window to an ideal scale-degree distribution for each of the 24 major and minor keys.) The key was labeled "ambiguous" if the highest key's correlation coefficient was less than 0.1 higher than the next highest correlation coefficient. Otherwise the best-correlated key was identified as the key of the window, with a "confidence value" equal to the correlation coefficient for that key. The key of each chord was then determined by comparing the eight windows containing that slice (excluding ambiguous windows). The key of the window having the highest confidence value was taken as the "local tonic" of the slice. We used this information to create the last four fields of each salami-slice record:
- LocalTonic: An integer modulo 12 corresponding to the local tonic, or the string "ambiguous".
- LocalMode: "Major," "minor," or "ambiguous."
- Confidence: The key-correlation coefficent described above.
- LocalSDNormalOrder: An element-wise transposition of PCNormalOrder by the interval required to normalize the local key segment to C major or minor.
The corpus is posted at ycac.yale.edu/downloads. The metadata appears as one file, and the data are compressed into three zip files: (1) "Great" composer files for Bach through Mozart, (2) "Great" composer files for Saint-Saëns through Wagner, and (3) alphabetically grouped files for those composers who did not receive enough uploads to warrant their own independent page on the classicalarchives.com website.
What the Corpus Represents
When compiling a musical corpus, a researcher must decide which composers and historical eras to sample, and which and how many pieces from those composers and eras to include, as well as along and what the criteria for consideration are (i.e., whether to include sketches, different versions of the same piece, etc.). The intended goals and uses of a corpus will inform these decisions. For instance, if one intended to produce a corpus that represents what a 21st century listener is likely to hear in his or her daily life, one might use the most popular recordings on a ubiquitous commercial site like Amazon.com. On the other hand, one could compile a corpus of works valued by a scholarly community by compiling the composers and pieces referenced in textbooks or musical encyclopedias (London 2013).
Since classicalarchives.com's collection arises from user uploads, and these uploaded files were constructed by the users themselves for no compensation, this collection reflects the priorities of a group of dedicated "classical" music lovers. The properties of the corpus result from the decisions made by the dozens of uploaders as to which composers and pieces they spent their time encoding. Unlike a corpus of commercially popular music or one compiled by professional scholars, the constituency of the YCAC is not determined by the preferences of many users nor by academic values. Rather, the choices about how to choose and weight composers, genres, and time periods, as well as what to consider as "pieces" were crowd sourced from the users of classicalarchives.com. While this results in "the usual suspects" – Bach, Beethoven, Mozart – having the strongest representation in the corpus, it also leads to the of inclusion of certain individual's personal favorites – e.g., the 12 Etudes of Charles-Valentin Alkan or Thomas Arne's 1740 British nationalist opera, Alfred. The YCAC, then, is neither an exhaustive collection of music written within some historical parameters, nor an emergent summary of the tastes of thousands of musical consumers, but rather a survey of the musical priorities of a group of individuals committed to converting their favorite pieces into a digital format.
Properties of the Dataset
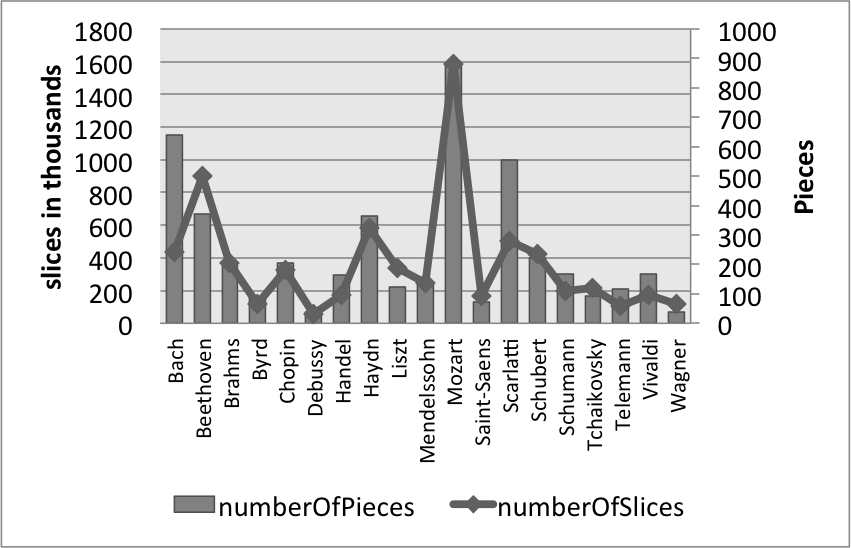
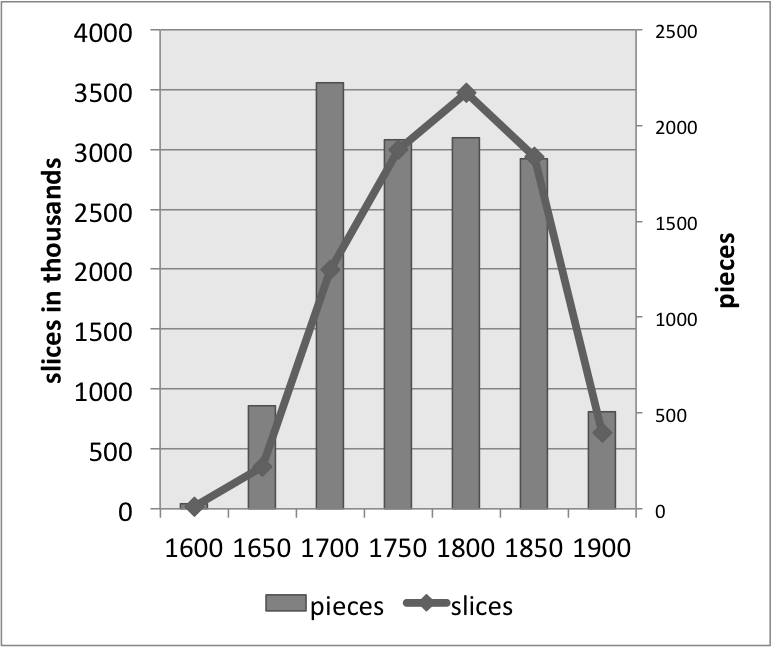
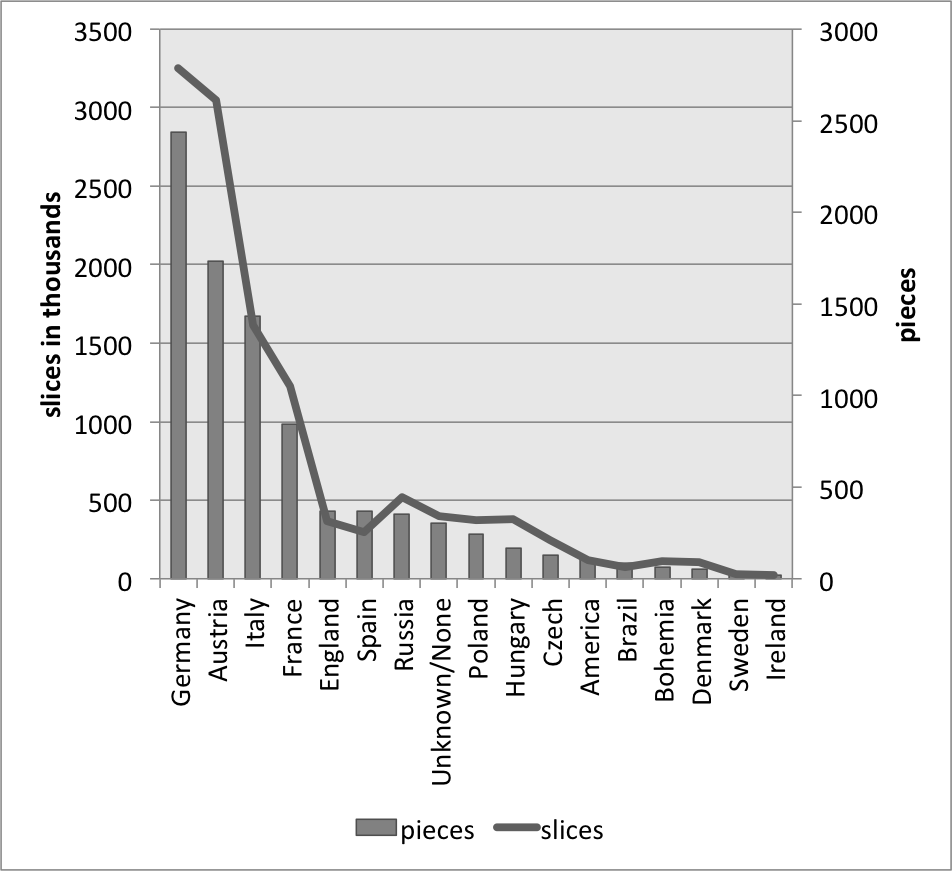
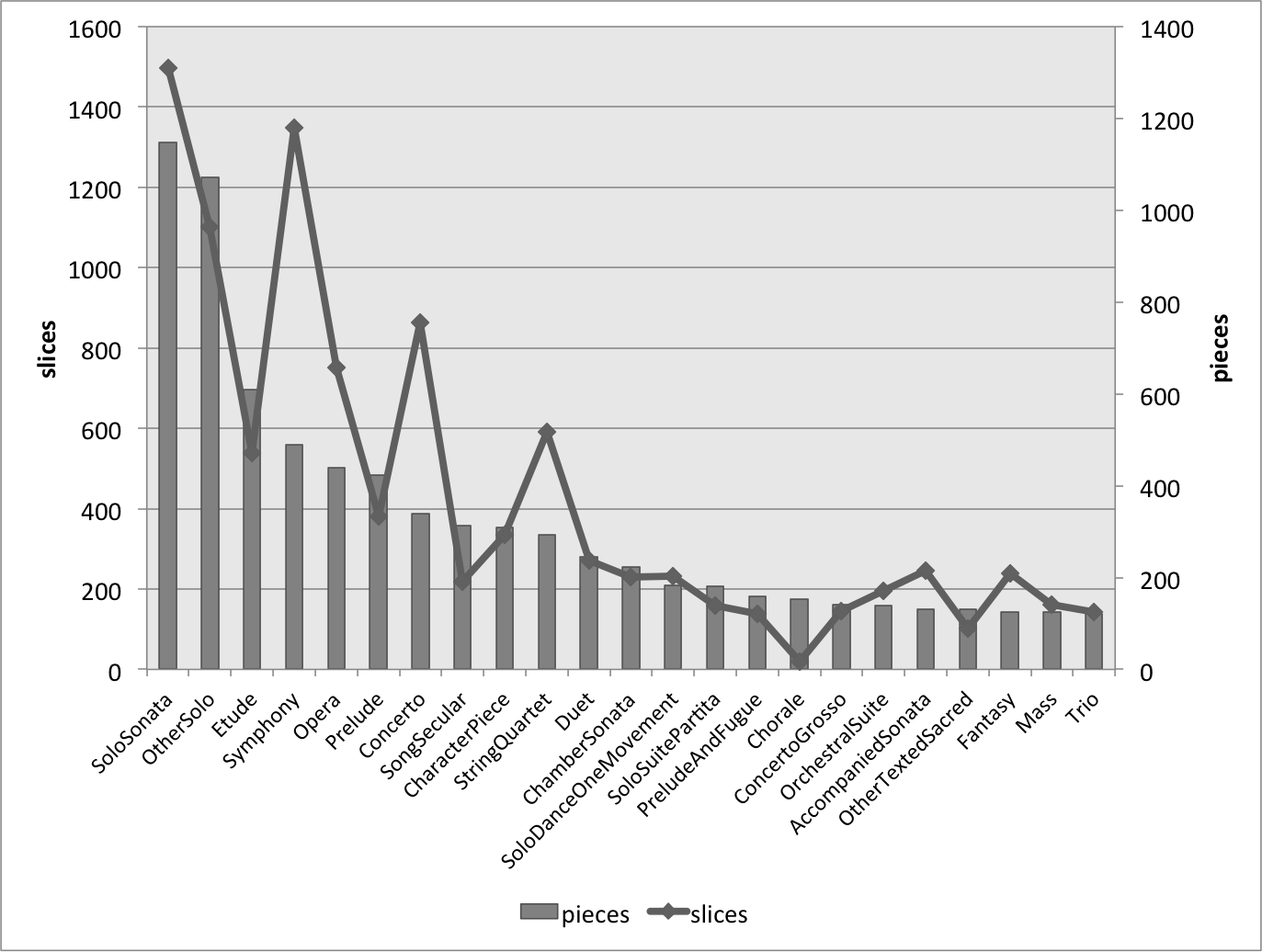
Figure 1 represents the size of the 19 most frequent composer's MIDI collections, with the bars illustrating the number of files (right-hand axis) and the line representing the total number of slices within in our CSV files (left-hand axis). Mostly, these two values track one another; however, in some cases the length of the files are consistently short enough that there are fewer slices than the number of pieces might suggest (e.g., Scarlatti), or the pieces are consistently long enough that there are fewer pieces than one might expect (e.g., Beethoven). Figures 2, 3, and 4 undertake the same representation for 50-year periods, nationalities, and genres within the whole corpus. While the numbers of slices and files tend to track one another, the two parameters are mismatched in genres that are either longer or more rhythmically active, both conditions that would create more salami slices – e.g., symphonies, operas, and string quartets – with the opposite holding true for the chorale genre.
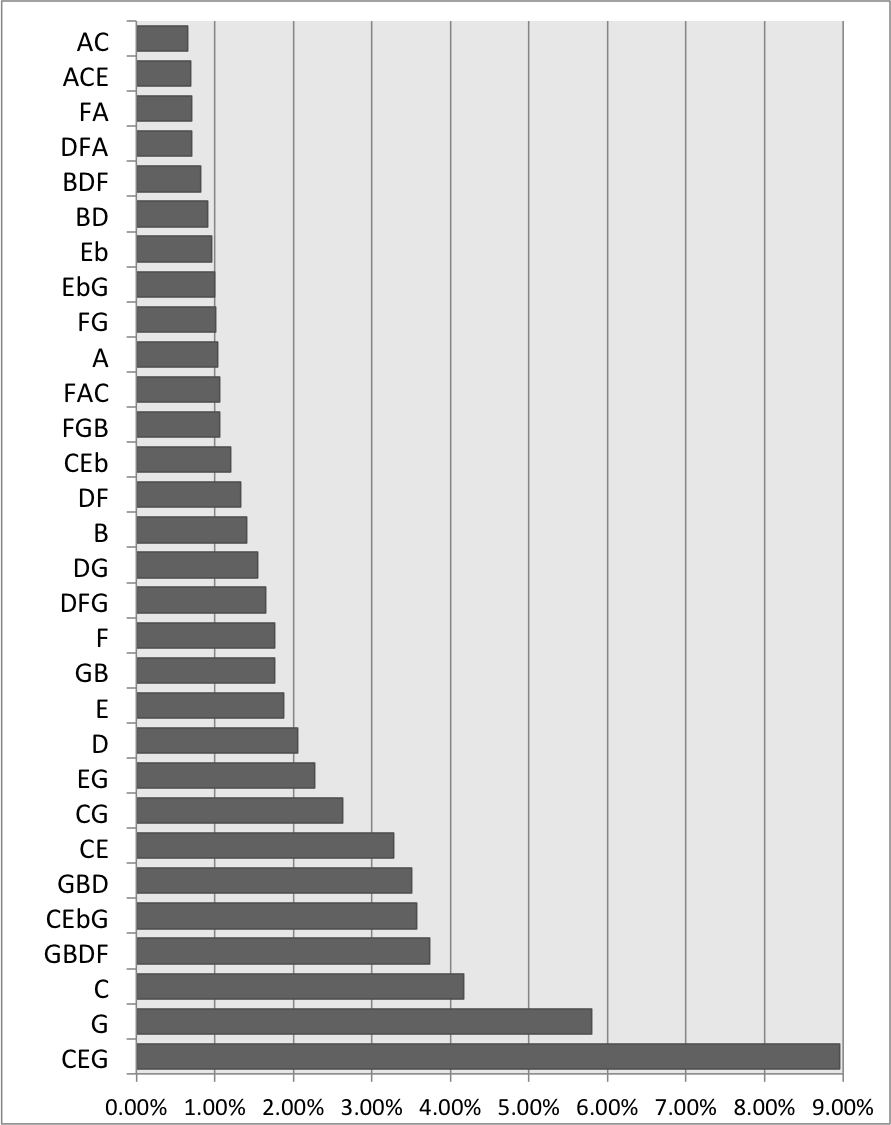
Figure 5 shows the most frequent scale-degree sets within the corpus by converting the modulo 12 scale degree sets to their pitch classes in C major/minor. The most frequent structures are a mixture of tertian chords and individual scale degrees: the tonic chord is the most frequent, constituting almost 9% of all slices, with the monad pitch classes C and G occupying the next two spots, at 5.79%, and 4.17% respectively. Note also that the dyadic subsets of the major tonic triad are present in the top 10.
Difficulties and Peculiarities of the Dataset
The structures shown in Figure 5 highlight both the power and peculiarity of the salami-slice method: it shows exactly what sorts of structures occur on the surface of this corpus, introducing no biases or assumptions about what is or is not a chord, and what structures should or should not reduced to or included in other structures. The simplicity of the data endows it with versatility: representing raw surface pitch and onset data provides researchers the flexibility to model the data in many different ways. However, this also means that, for example, the subsets of a tonic triad are not considered equivalent to a complete tonic triad. While some research has experimented with ways to introduce equivalencies into the alphabet of chord types (White 2013), the power and peculiarity of the YCAC's chord data should be noted.
One important musical parameter is notably absent from the dataset: meter. While MIDI files do include a metric parametic, it is set by default to common time (4/4) and resetting this parameter during the encoding process is not required. This means that if a classicalarchives.com contributor did not manually change a file's meter setting, a piece in 6/8 could be mistakenly encoded in 4/4. Similarly, MIDI does not have the capacity to encode an initial incomplete measure pickup; rather, the user must either change the meter for the initial measure or insert the proper number of rests at the beginning of a file to ensure that measures are properly aligned. Consider a piece in 4/4 with a quarter note pickup: if the encoder neither enters 3 quarter-note rests at the beginning of the file nor inserts an initial measure of 1/4, all downbeats will be displaced by a quarter note. Because of this, we did not include metric data in our corpus.
Similarly, the relative noisiness of this data needs to be recognized. These files were created by amateurs in their free time, and many were encoded through MIDI keyboard performance. This results in far more errors than would be found in professionally encoded corpora. In particular, many keyboard-encoded works are affected by the performer's articulation and technique: rolling chords can divide a vertical sonority into its constituent pitches, while a legato touch can make one chord bleed into the next. For instance, a recent study of a random sample of classicalarchives.com found that 8% of the encoded pitches within their sample did not match with the published score (Shanahan & Albrecht 2013). While these difficulties are not trivial, the size of the corpus somewhat mitigates the noise. It is also possible (as was suggested by the error-finding study) that performed encodings have far more error and noise than typed-in encodings, and therefore future research could potentially identify and exclude these errors by their noise level.
A Sample Case
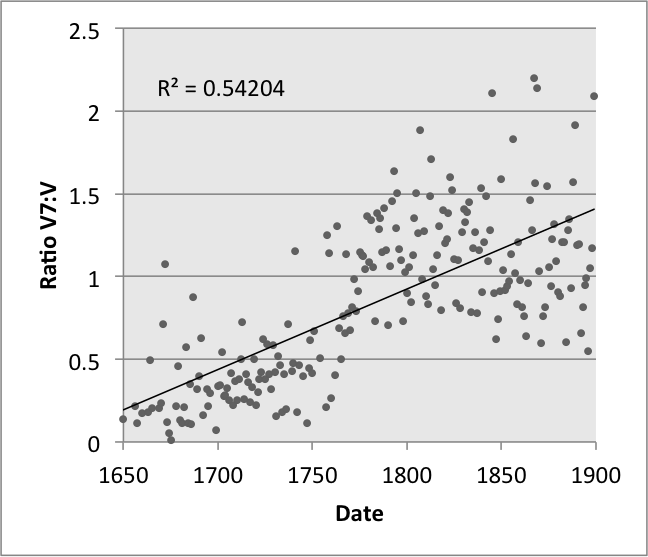
The size and metadata of this corpus makes it ideal to provide evidence for music theoretical intuitions, to show historical trends, or to model one musical characteristic as a function of another. For instance, one might have the intuition that later tonal composers preferred V7 chords over V chords, and that the inverse was true for earlier composers. Figure 6 uses the corpus' LocalSDNormalOrder and date parameters to show that this is indeed the case. The y-axis shows the ratio between the number of V7 chords and V chords: ratios below 1 indicate more V chords than V7s; ratios above 1 indicate the opposite. Plotting the ratio of V7 to V chords as a function of their year, we find a relatively strong upward trend, with an r2 of 0.542 between the year and the ratio.
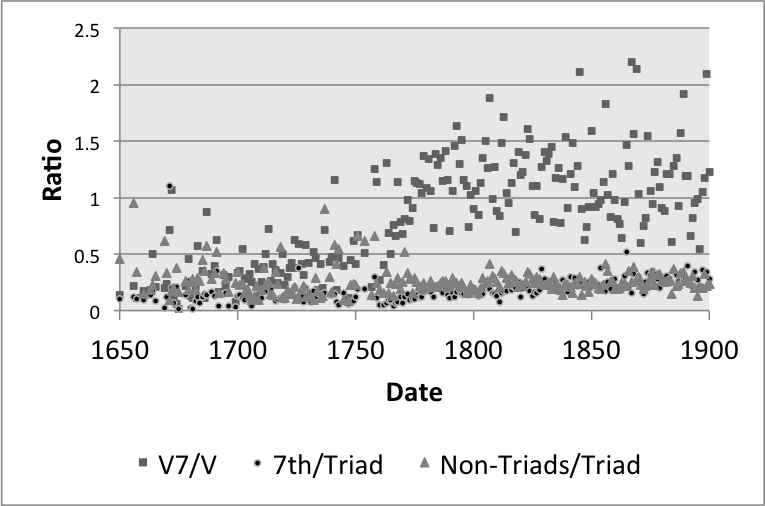
However, this trend could be due to an overall rise in the use of seventh chords, rather than dominant sevenths specifically; alternatively, it could be the case that there are simply more dissonant slices in later music. We can test this by using NormalForm data to plot the ratios of sevenths (excluding V7s) to triads (excluding V chords) and the ratios of all non-triads to triads (again, excluding V7 and V, respectively). Figure 7 adds these coordinates to Figure 6, and Table 1 shows the resulting correlation matrix between these vectors. Notice that the ratios of sevenths to triads increases at a comparable pace to that of dominant sevenths, but with more variation (r2 = 0.254), and the ratio of non-triads to triads does not correlate to date (r2 = 0.046). The rise in sevenths overall, however, does correlate to rise of dominant sevenths, with a coefficient of 0.398. Based on these results, we might claim that the rise in dominant sevenths accompanies a broader historical trend toward more sevenths, but these increases cannot be explained by a general trend towards non-triads.
| V7 : V | 7th : Triad | Non-Trd: Trd | |
| V7 : V | 1 | 0.398 | -0.037 |
| 7th : Triad | 1 | -0.175 | |
| Non-Trd : Trd | 1 |
ACKNOWLEDGEMENTS
The authors thank Pierre Schwob and Nolan Gasser of classicalarchives.com for their support. We also thank the Allen Forte Fund at Yale University and the NEH "Digging Into Data Grant" for their generous funding of the YCAC. Additional thanks to our research assistants: Joseph Salem, Ben Watsky, Joseph Marquez, and Baldwin Giang.
NOTES
-
Correspondence can be addressed to: Dr. Christopher White, UMass Amherst, 273 Fine Arts Center East, 151 Presidents Dr., Ofc. 1, Amherst, MA 01003-9330, cwmwhite@music.umass.edu.
Return to Text -
http://www.classicalarchives.com/about.html, referenced July 15, 2015
Return to Text -
Using nomenclature like "Western," "Classical," "Great," and "Early" to describe this repertoire is naturally problematic. We adopt these adjectives when describing the corpus because they were present in our source data: these terms are not retained in the YCAC.
Return to Text -
This term is an homage to György Ligeti, who described first conceiving his 1968 harpsichord piece Continuum as "a paradoxically continuous sound … that would have to consist of innumerable thin slices of salami" due to the characteristic envelope of a note played on the harpsichord.
Return to Text
REFERENCES
- Bertin-Mahieux, T., Ellis, D., Whitman, B., & Lamere, P. (2011) The Million Song Dataset. Proceedings of the 12th International Symposium on Music Information Retrieval Conference, 591–596.
- Bellman, H. (2005). About the determination of the key of a musical excerpt. Proceedings of the 3rd International Symposium, Computer Music Modeling and Retrieval, 187–203.
- Burgoyne, J.A., Wild, J., & Fujinaga, I. (2013). Compositional Data Analysis of Harmonic Structures in Popular Music. Proceedings of the 4th International Conference on Mathematics and Computation in Music, 52-63. http://dx.doi.org/10.1007/978-3-642-39357-0_4
- Cuthbert, M.S. & Ariza, C. (2011). music21: A Toolkit for Computer–Aided Musicology and Symbolic Music Data. Proceedings of the 11th International Symposium on Music Information Retrieval, 637–42.
- DeClercq, T. & Temperley, D. (2011). A Corpus Analysis of Rock Harmony. Popular Music, 30(1) 47–70. http://dx.doi.org/10.1017/S026114301000067X
- Duane, B. (2012). Agency and Information Content in Eighteenth- and Early Nineteenth-Century String-Quartet Expositions. Journal of Music Theory, 56(1), 87–120. http://dx.doi.org/10.1215/00222909-1546976
- London, J. (2013). Building a Representative Corpus of Classical Music. Music Perception. 31 (1), 68-90. http://dx.doi.org/10.1525/mp.2013.31.1.68
- Shanahan, D. & Albrecht, J. (2013). The Acquisition and Validation of Large Web-Based Corpora. Presented at the Conference for the Society for Music Perception and Cognition, Toronto, Canada.
- Temperley, D. (2009). A Statistical Analysis of Tonal Harmony. http://www.theory.esm.rochester.edu/temperley/kp-stats.
- White, C.W. (2013). An Alphabet-Reduction Algorithm for Chordal n-grams. Proceedings of the 4th International Conference on Mathematics and Computation in Music, 201–212. http://dx.doi.org/10.1007/978-3-642-39357-0_16