Introduction
SEVERAL acoustic factors are known to contribute to the perception of sadness. One factor is a darker timbre. In the case of speech, Scherer, Johnstone and Klasmeyer (2003; Table 23.2) note that sadness is linked to a greater spectral slope—that is, where the rate of energy decline with respect to frequency is greater for sad speech compared with other vocal affects. The darker timbre of sad speech appears to be caused by the relaxation of the zygomatic muscles, which pull the lips away from the teeth (in contrast to smiling where the lips are retracted against the teeth). This relaxation produces a lengthening of the vocal tract resulting in a lower resonant frequency, consequently causing a darker or less bright sound (Ohala, 1980, 1994; Tartter, 1980; Tartter & Braun, 1994).
In the case of music, several studies have identified plausible connections between various musical practices and known properties of sad speech. For example, Schutz, Huron, Keeton, and Loewer (2008) compared the distribution of major and minor modes in the concert repertoires of two similar musical instruments—marimba and xylophone. For the darker sounding marimba, roughly 60 percent of the active tonal repertoire is in the minor mode, whereas only 6 percent of the active tonal repertoire for the (considerably brighter) xylophone is in the minor mode. At face value, this result appears to support the connection between darker timbre and sadness. However, other interpretations are possible.
The marimba and xylophone are not exactly comparable instruments. The marimba is pitched an octave lower than the xylophone, and the marimba produces longer periods of sustain compared with the xylophone. On the one hand, sad speech also exhibits lower overall pitch, so the association between the marimba and the minor mode might originate in its lower pitch compared with the xylophone. On the other hand, sad speech exhibits a slower syllable rate and tempo, so the association between the marimba and the minor mode might originate in its slower decay compared with the xylophone—which is consequently less able to play at slow tempos. That is, timbre, pitch height, and tempo are confounded when comparing these two instruments.
A similar confound is evident when contrasting music for guitar and banjo. The banjo exhibits a brighter timbre than the guitar. In addition, the banjo exhibits shorter sustain than the guitar. So the greater association of sad music with the guitar may theoretically be attributable to either or both of those features. (As Steve Martin famously said: "You can't play sad music on a banjo"—see Huron, Anderson, & Shanahan, 2014.) Johnson (2010) addressed this issue by comparing the note-rates for performances of the same works on solo guitar and solo banjo. He found that the note rates for banjo renditions of the same work were considerably faster than those for the guitar, suggesting that tempo is an important factor, even apart from the difference in timbre between these two instruments. Both the Schutz et al. (2008) and Johnson (2010) studies demonstrate the difficulty of isolating different acoustical factors in creating nominally sad textures.
The goal for the current study was to test the "darker is sadder" hypothesis using yet another ethological approach. When performing on stringed instruments some sounds are played on "open" strings, whereas other sounds are played using "stopped" strings in which the player uses a finger from the left hand to press the string against the fingerboard. Especially in the case of unfretted instruments, performers agree that stopped and open strings produce different timbres. Open strings vibrate the full length between the bridge and the nut, and the hard edge of the nut produces a well-defined end-point for the vibrating string. Unlike unfretted instruments, stopped strings are terminated by the fleshy pad of the finger, producing a less well-defined end-point with the finger absorbing high-frequency vibrational energy compared with the nut (Schelleng, 1973). As a result, open strings are widely regarded as brighter sounding than stopped strings. This effect is less marked in the case of fretted instruments like the guitar. With the guitar, depressing the finger causes the string to make contact with a metal fret strip, which acts as the end-point for the vibrating string rather than the pad of the finger.
If stopped strings exhibit darker timbres than open strings, one might expect that nominally "sad" works for stringed instruments might tend to avoid the use of open strings in contrast to nominally "happier" works. At the same time, there are other good reasons why musicians might prefer stopped strings over open strings. Most notably, stopped strings afford the use of vibrato, which in modern orchestral music-making is a nearly omnipresent element of preferred performance practice. In the case of orchestral strings, if we find evidence of a preference for stopped strings as opposed to open strings, we cannot distinguish between the claims that the goal of this practice is strictly timbre- or vibrato-related. In this study, we acknowledge that our method cannot distinguish between these competing claims. Perhaps future studies may be able to disambiguate the principal motivation for any presumed preference for stopped over open string use. In any event, it is appropriate to test empirically the conjecture that musicians prefer stopped string use over open string use—at least in the case of nominally sad music.
Preliminary Test
The current study was motivated by the results of an informal examination of Samuel Barber's Adagio for Strings. The Adagio was originally written as the middle movement of a string quartet (opus 11) and later arranged for string orchestra. In 2004, the British Broadcasting Corporation's World Service conducted an international survey where listeners voted for "the world's saddest music." Samuel Barber's Adagio for Strings won an outright majority of votes—although empirical research suggests that the Adagio may not be as "sad" as commonly supposed (Baumgartner, Esslen & Jancke, 2006; Boltz, 2001; Krumhansl, 1997; Nawrot, 2002). The work's key is unusual (B-flat minor), and this led us to explore the possibility that Barber intentionally aimed to reduce the potential for open strings, either in order to facilitate the use of vibrato or to increase the darkness of the string timbres or both. We tallied the proportion of potentially open-to-stopped strings and applied this method to 12 alternative transpositions. The results are displayed in Figure 1 (next page). As can be seen, the results are unequivocal: the key chosen by Barber (B-flat minor) is clearly the best possible key if the aim is to minimize the possibility of playing notes using open strings. This raises the question of whether Barber's practice might be indicative of a general musical practice—hence motivating the current study.
Hypothesis
Formally, our hypothesis may be stated as follows:
H1. The ratio of open-to-stopped strings will be smaller for sad works compared to non-sad works for strings.
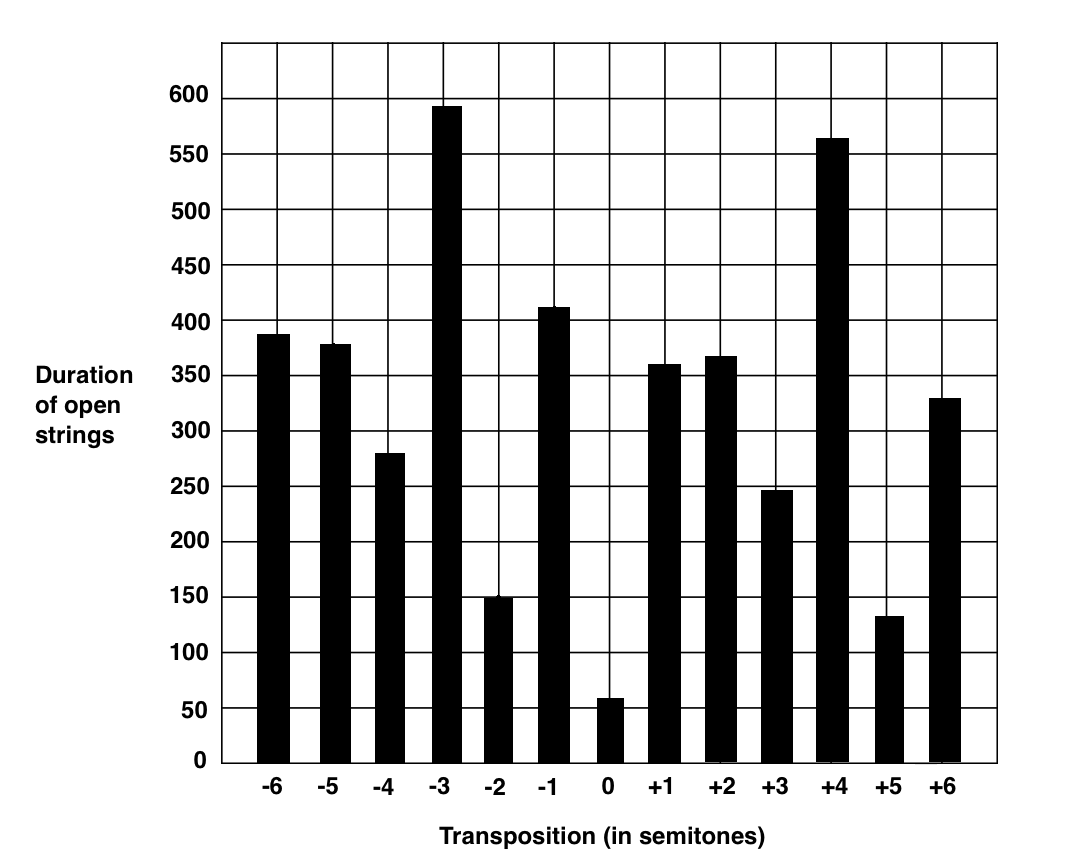
Fig. 1. Effect of transposition on total duration of potentially open-string tones in Samuel Barber's Adagio from his opus 11 string quartet. Duration is measured in quarter-note units. Transpositions (in semitones) range from a tritone below (-6) to a tritone above (+6). The original key (0, B-flat minor) exhibits a notable minimum, consistent with the conjecture that Barber aimed to avoid the possibility of instrumentalists playing with open strings.
In order to test this hypothesis we need to operationalize each of the terms. For the purposes of this study, we will consider only common orchestral stringed instruments—specifically, the violin, viola, and violoncello. In playing these instruments, performers have considerable latitude in choosing to play a given tone using an open or stopped string. For example, a violinist can play the pitch D4 using either the open D string, or by playing a stopped tone on the G string. With the exception of the lowest pitch (G3), all of the pitches playable on the violin can be theoretically played using a stopped string. The most accurate way of determining whether a given note is played using an open or stopped string would be to study video recordings with close-ups of the left (fingerboard) hand. However, this approach was deemed impractical since we aim to calculate the ratio of open-to-stopped strings using a large musical sample. Instead, we elected to focus on the musical notation. In the notation, one can distinguish between those pitches that must be played using a stopped string from those pitches that may be played using an open string. While the performer holds some latitude to play potentially open string pitches using a stopped string, one might suppose that a composer, aiming to encourage the use of stopped strings would simply minimize those pitches that could potentially be played using an open string. Accordingly, we will calculate the ratio between "potentially open string pitches" and "stopped-string pitches."
Turning next to the term "sad music," one way of operationally defining sad music might simply be to select works in the minor mode. However, not all works in the minor mode may be reasonably characterized as "sad." Post and Huron (2009) observed a general association between slow tempo and the minor mode—consistent with the notion that slow tempo contributes to the perception of sadness. However, they found a notable exception in music from the nineteenth century, which exhibits a reverse correlation: in the nineteenth century, on average, music in the minor mode exhibits faster tempos than major mode works. In order to avoid this possible confound, we chose to operationally define sad music as music in the minor mode that is also slow in tempo.
Method
Sample
As noted earlier, a preference for stopped strings may have several possible motivations. Apart from the pursuit of a darker timbre, stopped strings also enable the use of vibrato. Note that prior to the 20th century, it is thought that vibrato was used in an intermittent or ornamental fashion; the use of constant vibrato throughout the work was not yet mandatory (Norrington, 2004). Accordingly, in our musical sample we will explicitly examine music prior to around 1850. To this end, we made use of a convenience sample of already-existing computer encodings of string quartets from the 18th and 19th centuries. The works were available in a database provided by the Center for Computer Assisted Research in the Humanities (http://kern.ccarh.org). Our initial candidate sample included a total of 73 string quartets: 46 string quartets by Franz Joseph Haydn, 19 string quartets by Wolfgang Amadeus Mozart, 7 string quartets by Ludwig van Beethoven, and 1 string quartet by Franz Schubert. More specifically, we selected the conventional "slow" movements from these string quartets. Typically, this is the second movement in both three-movement and four-movement works.
Procedure
For each string quartet, we examined the various movements and determined whether the prevailing mode was major or minor. We divided the movements of the 73 quartets into three categories: (1) obviously predominantly major, (2) obviously predominantly minor, and (3) not obviously major or minor. Of the slow movements from these quartets only 11 movements met the a priori selection criterion of being both slow and obviously minor. Five were composed by Haydn, and three each were composed by Mozart and Beethoven. The Schubert quartet failed to be included in the sample. For technical reasons, only 10 of the 11 selected movements were available for analysis.
For each of the 10 minor-mode slow movements, we randomly selected one of the remaining movements from the same quartet as a control. In order to be selected, control movements must be deemed obviously in the major mode. None of the string quartets failed to include a movement deemed obvious major, so control major-mode movements were available for each of the 10 target minor-mode slow movements. Note that a control movement might also have a relatively slow tempo marking. For example, one of the control movements was marked "Adagio e cantabile" and a second was marked "Adagio - Allegro assai - Adagio." However, the majority of control movements were clearly faster in tempo, ranging from Andante to Presto, with a considerable majority exhibiting some type of allegro tempo. Regardless, major-mode movements were retained as controls whether or not the tempo was fast or slow.
For both the target and control movements we counted the number of notes for each instrument, and also counted the number of notes that could, in principle, be played using open strings. Separate tallies were done for each of the target instruments: violin I, violin II, viola, and violoncello. Tied notes were treated as single pitches. In order to maximize data independence, repeats and Da Capos were ignored.
Results
Recall that our hypothesis predicts that the ratio of open-to-stopped strings will be smaller for nominally sad works compared to non-sad works for strings. In our operationalization, we have assumed that slow works in the minor mode are more likely to express or represent sadness compared with tempo-variable works in the major mode. Accordingly, we would expect that slow-minor movements should exhibit fewer potential open strings than for major movements. Combining the data for all of the sampled works, we determined that for slow-minor movements, 17.5 percent of all notes could possibly be played using open strings. By comparison, for tempo-variable major movements 15.9 percent of notes could be played using open strings. In short, the results are exactly contrary to our hypothesis. Major-mode movements have fewer potential open strings than slow-minor movements. No statistical test is necessary since the average scores are skewed opposite to the predicted direction.
Another way to test the hypothesis might compare the original keys with all other possible keys in which a work might be written—as we did in our exploratory study with Barber's Adagio. For example, a work might be written in B minor—a key that affords relatively few opportunities to use open strings, compared with other possible keys. Accordingly, we can calculate the ratio of potentially open-to-stopped strings for all possible chromatic transpositions, and compare the transposed ratios to the ratio for the actual notated key. To this end, we transposed each movement to 11 different transpositions (ranging from a tritone below the notated key to a perfect fourth above the notated key). For each transposition we calculated the proportion of potentially open and stopped strings. These transposed versions effectively provide a distribution against which the ratio of open-to-stopped strings in the notated key can be compared. The actual open-to-stopped ratio can then be expressed as a normalized value or z-score. Positive z-scores indicate that the actual key provides more open-string opportunities than other possible keys. Table 1 reports the average z-scores for open strings for the two musical samples (slow-minor and tempo-variable major) with independent results shown for each instrument, as well as a combined score.
| Instrument | Slow-minor | Major |
|---|---|---|
| Violin | +0.90 | +1.96 |
| Viola | +2.05 | +1.44 |
| Cello | +2.04 | +0.92 |
| All | +1.59 | +0.34 |
Positive z-scores indicate that the actual key involves more open strings than would be expected compared with a random transposition or random key. As can be seen in Table 1, there is a proliferation of positive z-scores. This means that, in general, the notated keys exhibit more open strings than would be expected (were key not considered) for both the slow-minor and major movements. Moreover, the overall z-score for slow-minor movements is higher than for major-mode movements indicating that the open-string tendency is greater for the composer-selected keys in the nominally sadder movements. Once again, these results are contrary to the motivating hypothesis for this study. As before, no statistical tests are necessary since the results are skewed in a direction opposite to the hypothesis.
Sympathetic Vibration — A Post Hoc Test
In discussing our negative results with string players, another possibility was raised, namely the role of sympathetic vibrations. When one plays C3 on the cello, the lowest string (C2) will typically vibrate as well. This phenomenon of sympathetic vibration can be observed for all of the lower harmonics, so the C string will tend to vibrate sympathetically for the pitches C3, G3, C4, etc. Similarly, the pitches G3, D4 and G4 will tend to evoke sympathetic vibration from the G (G2) string, and so on. The consequence of these sympathetic vibrations is described by string players as adding brightness to the timbre—analogous to the brightness of open strings. Accordingly, instead of just focusing on the potential open strings, we might also consider the effect of those pitches that could evoke sympathetic vibrations. As a result we might entertain the following post-hoc variation to our experimental hypothesis, namely:
H2. The ratio of open-and-or-sympathetic to stopped-and-nonsympathetic strings will be smaller for sad works compared to non-sad works for strings.
In brief, we employed the same method and same musical sample described above, with the addition of the nominally "sympathetic" pitches. In general, strings will vibrate sympathetically to any concurrent tone that corresponds to a harmonic of that string. The amount of energy of the sympathetic vibration is dependent on the energy of the concurrently sounded tone, as well as the closeness in frequency to the true harmonic. Harmonics 5 and 7 are notably out-of-tune with their equally-tempered counterparts, so most sympathetic vibrations will be limited to harmonics 1, 2, 3, 4, 6, and 8. Of course pitches played below a given string may also activate sympathetic vibration for an open string tuned above. Hence, on the cello, playing A2 on the G string will tend to engage the open A string (A3). Applying these observations, Tables 2, 3, and 4 identify the strings for each of the violin, viola and violoncello, as well as the corresponding near-harmonic pitches that are most likely to evoke sympathetic vibrations. In creating these lists, note that a distinction must be made between the evoking pitch and the evoked pitch. For example, playing the G (G3) string on a violin might evoke a sympathetic vibration on the D (D2) string, corresponding to the third harmonic for G3, namely D5. In this case, G3 is the evoking pitch and D5 is the evoked pitch. Although it is D5 that is evoked, it is the brightness of the G3 string that is enhanced. Hence, for the purposes of this study, our interest is not the evoked pitch (e.g., D5), but the evoking pitch (G3).
| String | Sympathetic tones (2nd, 3rd, 4th, 6th, 8th harmonics) |
|---|---|
| G3 | G4, D5, G5, D6, G6 |
| D4 | D5, A5, D6, A6, D7 |
| A4 | (A3), A5, E6, A6, E7, A8 |
| E5 | (E4), (A4), E6, B6, E7, B7, E8 |
| String | Sympathetic tones (2nd, 3rd, 4th, 6th, 8th harmonics) |
|---|---|
| C3 | C4, G4, C5, G5, C6 |
| G3 | G4, D5, G5, D6, G6 |
| D4 | (D3), D5, A5, D6, A6, D7 |
| A4 | (A3), (E5), A5, E6, A6, E7, A7 |
| String | Sympathetic tones (2nd, 3rd, 4th, 6th, 8th harmonics) |
|---|---|
| C2 | C3, G3, C4, G4, C5 |
| G2 | G3, D4, G4, D5, G5 |
| D3 | (D2), D4, A4, D5, A5, D6 |
| A3 | (A2), (E4), A4, E5, A5, E6, A6 |
In effect, we treated all of the pitches listed in Tables 2-4 like open strings, and repeated our analysis of the Haydn, Mozart, and Beethoven minor-slow and tempo-variable major movements. For simplicity, we will collectively refer to all of the pitches displayed in Tables 2-4 as "sympathetic pitches" rather than as "open+sympathetic pitches."
Combining the data for all of the sampled works, we determined that for slow-minor movements, 45.1 percent of all notes are "sympathetic" pitches. By comparison, for tempo-variable major movements 41.9 percent of notes are sympathetic pitches. As before, the results are exactly contrary to our hypothesis. No statistical test was deemed necessary since the average scores are skewed opposite to the predicted direction.
Once again, we transposed all of the movements through 12 different keys—down to a tritone below, and a perfect fourth above, as well as the original key. The proportion of sympathetic pitches for the transposed versions were again used as a distribution against which the actual sympathetic pitch counts could be compared—resulting in a set of normalized z-scores. Table 5 reports the z-scores for sympathetic notes for the two musical samples (slow-minor and major) with independent results shown for each instrument, as well as a combined score.
| Instrument | Slow-minor | Major |
|---|---|---|
| Violin | +1.22 | +1.81 |
| Viola | +1.65 | +1.83 |
| Cello | +1.73 | +1.75 |
| All | +0.99 | +1.82 |
As before, positive z-scores indicate that the actual keys involve more sympathetic notes than would be expected compared with a random transposition or random key. As can be seen, all of the values are positive suggesting that the actual keys involve more sympathetic notes than expected. However, the values for the major mode are bigger than comparable values in the minor mode, suggesting that major-mode movements exhibit a greater tendency to avoid sympathetic notes than slow-minor movements—exactly contrary to our hypothesis.
Conclusion and Discussion
As we have seen, both our original and post hoc hypotheses failed. It may be appropriate to speculate about possible reasons for this failure. In the first instance, the hypotheses may simply be false. It may be that the results for Barber are unique, a chance result, or that Barber was an idiosyncratic composer interested in reducing the possibility of open-string playing. There are other possibilities as well.
One possibility is that the composers studied here were already aware of the preference string players have for playing stopped strings. In general, string players much prefer to play stopped rather than open strings, so even in a key (such as C major) with the potential for many open strings, players typically choose to play using entirely stopped strings. At the same time, for very rapid passages, open strings may tend to reduce the difficulty. Both Mozart and Haydn were experienced string players and Beethoven was certainly well versed in string technique (Drabkin, 1995). Perhaps they were providing more options for string players: that is, one could choose to play with or without open strings depending on the skill level of the performer or whether the work was being sight-read (Jones, 2003).
Other possibilities for the failure of our hypotheses might arise because the sample size was too small, or that the sample was restricted to just three composers from the late 18th and early 19th centuries. Note that Barber's Adagio was written more than a century after than the latest work in our sample. So the hypothetical compositional practice of avoiding open strings in nominally sad music might be a comparatively late compositional development. Alternatively, it may be that our use of minor-slow movements as representative of "sadness" or tempo-variable major movements as "non-sad" may be inaccurate or inappropriate.
The results of our post-hoc test reinforce the test results for our main hypothesis. Even when the possibility of sympathetic vibration is taken into account, slow-minor movements do not tend to avoid the possibility of open strings more than tempo-variable major mode movements—at least for the composers studied.
Existing research suggests that musicians tend to take advantage of the expressive opportunities afforded by various instruments and playing techniques (e.g., Gimenes, & Manzolli, 2006; Horton, 1986; Huron, Anderson & Shanahan, 2014; Huron & Berec, 2009; Jiranek, 1971; Schutz, et al., 2008; Sudnow, 1978). Recall that the initial motivation for this study was the conjecture that nominally sad musical expressions might gravitate toward the use of darker timbres—as evident in sad speech. This idea gained credence following our exploratory analysis of Samuel Barber's Adagio, opus 11. However, this single case study did not generalize to a larger sample of string quartets by Haydn, Mozart and Beethoven. Are stopped strings preferred in sad music? With the notable exception of Barber's Adagio for Strings, perhaps not.
NOTES
-
Please address all correspondence to: David Huron, School of Music, 1866 College Rd., Columbus, OH, 43210, U.S.A, or to Caitlyn Trevor at trevor.5@osu.edu.
Return to Text
REFERENCES
- Baumgartner, T., Esslen, M., & Jancke L. (2006). From emotion perception to emotion experience: Emotions evoked by pictures and classical music. International Journal of Psychophysiology, 60, 34-43. https://doi.org/10.1016/j.ijpsycho.2005.04.007
- Boltz, M.G. (2001). Musical soundtracks as a schematic influence on the cognitive processing of filmed events. Music Perception,18, 427-454. https://doi.org/10.1525/mp.2001.18.4.427
- Drabkin, W. (1995). Beethoven and the open string. Music Analysis, 4(1-2), 15-28.
- Gimenes, M., & Manzolli, J. (2006). Técnicas e "affordances" instrumentais: Um modelo para a performance e a criação na música contemporânea. [Instrumental techniques and affordances: A model for performance and creation in contemporary music]. In: XVI Congresso da Associação Nacional de Pesquisa e Pós-graduação em Música. Brazil: ANPPOM, pp. 288-293.
- Horton, C. (1986). The identification of idiomatic writing for the horn. DMA dissertation, School of Music, University of Wisconsin, Madison.
- Huron, D., Anderson, N., & Shanahan, D. (2014). You can't play sad music on a banjo: Acoustic factors in the judgment of instrument capacity to convey sadness. Empirical Musicology Review, 9(1), 29-41. https://doi.org/10.18061/emr.v9i1.4085
- Huron, D., & Berec, J. (2009). Characterizing idiomatic organization in music: A theory and case study of musical affordances. Empirical Musicology Review, 4(3), 103-122.
- Jiranek, J. (1971). Statistika jako pomocny nastroj intonacni analyzy [Statistics as a tool in analysis of so-called idiomatic characteristics.] Hudebni veda, 8 (2), 165-182.
- Johnson, R.B. (2010). Selected topics in the perception and interpretation of musical tempo. PhD dissertation, School of Music. Ohio State University.
- Jones, R.M. (2003). Modulation by key class. Indiana Theory Review, 24, 1-27.
- Krumhansl, C. (1997). An exploratory study of musical emotions and psychophysiology. Canadian Journal of Experimental Psychology, 51(4), 336-352. https://doi.org/10.1037/1196-1961.51.4.336
- Nawrot, E.S. (2003). The perception of emotional expression in music: Evidence from infants, children and adults. Psychology of Music, 31(1), 75-92. https://doi.org/10.1177/0305735603031001325
- Norrington, R. (2004). The sound orchestras make. Early Music, 32(1), 2-5. https://doi.org/10.1093/earlyj/32.1.2
- Ohala, J. (1980). The acoustic origin of the smile. Journal of the Acoustical Society of America, 68, S33. https://doi.org/10.1121/1.2004679
- Ohala, J. (1994). The frequency code underlies the sound-symbolic use of voice pitch. In L. Hinton, J. Nichols & J. Ohala (Eds.), Sound Symbolism (pp. 325-347). Cambridge: Cambridge University Press.
- Post, O., & Huron, D. (2009). Music in minor modes is slower (except in the Romantic Period). Empirical Musicology Review, 4(1), 1-9.
- Schelleng, J.C. (1973). The bowed string and the player. Journal of the Acoustical Society of America, 53 (1), 26-41. https://doi.org/10.1121/1.1913322
- Scherer, K.R., Johnstone, T., & Klasmeyer, G. (2003). Vocal expression of emotion. In R. Davidson, K. Scherer, & H. Goldsmith (Eds), Handbook of Affective Sciences (pp. 433-456). Oxford: Oxford University Press.
- Schutz, M., Huron, D., Keeton, K. & Loewer, G. (2008). The happy xylophone: Acoustic affordances restrict an emotional palate. Empirical Musicology Review, 3(3), 126-135.
- Sudnow, D. (1978). The ways of the hand; The organization of improvised conduct. Cambridge, Massachusetts: Harvard University Press.
- Tartter, V.C. (1980). Happy talk: Perceptual and acoustic effects of smiling on speech. Perception & Psychophysics, 27(1), 24-27. https://doi.org/10.3758/BF03199901
- Tartter, V.C. & Braun, D. (1994). Hearing smiles and frowns in normal and whisper registers. Journal of the Acoustical Society of America, 96, 2101. https://doi.org/10.1121/1.410151

