INTRODUCTION
NEARLY 100 years ago, in 1921, the Viennese composer Arnold Schoenberg developed a "method of composing with twelve tones" (Schoenberg, 1941/1950). Schoenberg's approach began with a twelve-tone row, which assigned an order to the twelve tones of the chromatic scale. Because each "tone" could be used in any octave, it was actually what would later be called a "chroma" in psychology, or a "pitch class" in music theory. The tone row provided the basis for all of a composition's harmonic and melodic material. In addition to using the tone row in its original, basic, or prime form, a composer could use the tone row in three derived forms: retrograde, which turned the tone row backward; inversion, which turned the tone row upside-down by inverting all its intervals; or retrograde inversion, which did both. 2 In addition, any form of the row could be transposed by moving every chroma up (or down 3) by 1 to 11 semitones.
The twelve-tone approach to composing music had two psychological goals. The first goal was to give a composition what Schoenberg (1941/1950, p. 215) called "comprehensibility." The row would "function in the manner of a motive" (Schoenberg, 1941/1950, p. 219), unifying the composition much as motives or themes helped to unify compositions in older musical styles: "The relaxation which a satisfied listeners experiences when he can follow an idea, its development, and the reasons for such development is closely related, psychologically speaking, to a feeling of beauty. Thus artistic value demands comprehensibility, not only for intellectual, but also for emotional satisfaction" (Schoenberg, 1941/1950, p. 215). Schoenberg argued that the use of a twelve-tone row could help to deliver that satisfaction.
By itself, though, the use of a twelve-tone row was not enough to provide psychological coherence. One concern was that the length of the row might tax listeners' memory. "In point of fact," two music theorists later wrote (Morris & Alegant, 1988, p. 74), "few musicians, when presented with an arbitrary string of twelve pcs [pitch classes], find it an easy task to remember the series accurately, even after many hearings." Empirically, this statement was overly pessimistic, but the general concern that it raised was valid. In controlled experiments, musically trained listeners could in fact recognize, with over 90 percent accuracy, literal repetitions of the prime row when played with all notes the same length and in the same register (Krumhansl et al., 1987, Experiment 2; Pedersen, 1975). In one experiment, though, recognition fell all the way to chance levels when some pitches were displaced by an octave (Pedersen, 1975). In other experiments, recognition fell more than halfway to chance levels when the row was presented in inversion, retrograde, or retrograde inversion, or when the row was played with varied rhythms and phrasing such as might occur in an actual composition (Bruner, 1984; de Lannoy, 1972; Krumhansl et al., 1987 Experiments 2-3).
Schoenberg (1941/1950) recognized that, because of their cognitive challenges, twelve-tone compositions sometimes "failed to gain understanding," (p. 215) and he recommended several practices to ease listeners' burden. He recommended associating the row, or part of it, with a particular rhythm and phrasing "so that it can easily be recognized" (Schoenberg, 1941/1950, p. 220; cf. Huron, 2001 on similar approaches to distinguishing motives in tonal music). Schoenberg (1941/1950) recommended sticking with the prime form of the row in the early part of a composition, delaying transposition, retrograde, and inversion until later, furthermore expressing that "the set is often divided into groups; for example, into two groups of six tones, or three groups of four, or four groups of three tones." (p. 226) These internal tone-groups were often related to each other by transposition, retrograde, or inversion, so that the whole twelve-tone row could be "derived," to use a later theorist's term (Babbitt, 1955), from a shorter row of two, three, four, or six tones. Ostensibly, this eased the listener's task because the original twelve-tone row was now "a series of two or more 'chunks,' each of whose length is below the limit of 'the magic number seven, plus or minus two'" (Miller, 1956; quoted in Morris & Alegant, 1988).
The second goal of twelve-tone music was to give all twelve chromas equal weight and avoid defining one as a tonal center, tonic, or key. In twelve-tone music, it would be impossible to say that a passage of any length was in C Major, say, or F♯ Minor. As Schoenberg (1941/1950, p. 246) wrote, "the emphasis given to a tone by a premature repetition is capable of heightening it to the rank of a tonic. But the regular application of a set of twelve tones emphasizes all the other tones in the same manner, thus depriving one single tone of the privilege of supremacy. It seemed in the first stages immensely important to avoid a similarity with tonality." The effect, which Schoenberg had also tried to achieve before the twelve-tone revolution, was often labeled atonal.
The term atonal, however, was not popular with Schoenberg or other twelve-tone composers. While different composers criticized the term for different reasons, 4 a recurring theme was that listeners sometimes heard twelve-tone and other nominally atonal music with tonal ears. To put the argument in modern psychological terms, tonality is a well-learned schema that listeners try to apply to music persistently, even when it fits poorly. Igor Stravinsky (1970, p. 186), who adopted the twelve-tone method in the 1950s, once wrote that he did not consider his new music "atonal" because "that would be tantamount to saying that I had become deaf to tonality," which he had not. In an interview, composer Walter Piston described string quartets playing Schoenberg:
When they play any little phrase, they will hear it in some key—it may not be the right one, but the point is they will play it with a tonal sense. And it isn't only the players; it's also the listeners. They will hear tonality in everything. (Piston & Westergaard, 1968, p. 15).
Indeed, it is possible for a twelve-tone piece to evoke a sense of tonality, especially if the tone row includes tonal elements such as major or minor triads or scale fragments. Perhaps the best-known example is the tone row from the Violin Concerto by Schoenberg's student Alban Berg. Berg's tone row, shown in Figure 1, is composed of an extended chain of triads, followed by a short scale fragment. Its first seven notes are the notes of the G melodic minor scale, and the remaining notes fit G♯ melodic minor. When this row is used in Berg's Violin Concerto, there are many passages that sound as though they are in, or passing through, G Minor, A Minor, and other keys.
While tonally evocative rows, like the one from Berg's Violin Concerto, are well-known, what we will demonstrate in this article is that many other twelve-tone rows studiously avoided and undermined tonal schemata, taking pains not to evoke a tonal schema, or to nip it in the bud if it did arise. A genuinely atonal row, written as though tonal schemata did not exist, would occasionally include a triad or a major or minor scale fragment by chance, if not to serve some other musical purpose. But listeners' tonal schemata are so strong that composers who want to avoid them cannot afford to ignore tonality. They must actively work to undermine it.
This idea is not novel. In an interview, Walter Piston described teaching a young composition student who claimed not to "use" tonal harmony.
"Well," I say, "somebody will hear this chord over here and think, hmm, G,B,D…. How about that?" He objects, "You aren't supposed to hear it that way." Now, I think that's just whistling in the dark to say you're not supposed to. The fact is you do. (Piston & Westergaard, 1968, p. 13)
Stravinsky (1970, p. 38) explained that, while he could not ignore tonality, he could choose to work with or against it, and often did both within the same composition:
Now it may well be that I remain for a considerable time within the bounds of the strict order of tonality, even though I may quite consciously break up this order for the purposes of establishing a new one. In that case I am not atonal, but antitonal.
Experiments have confirmed that listeners can respond to twelve-tone music either tonally or anti-tonally. In one experiment (Krumhansl et al., 1987, Experiment 1), fragments from a twelve-tone rows were interrupted and listeners were played potential continuations ("probe tones") and asked to rate them. Some listeners responded tonally, giving high ratings to continuations that increased the row's fit to some major or minor key. Other listeners, most of whom had more musical training, responded anti-tonally, giving high ratings to continuations that reduced the row's fit to any major or minor key.
Huron (2006, pp. 339-344), who used the word "contra-tonal" instead of anti-tonal, reported that most tone rows of Schoenberg were anti-tonal, with a footnote (footnote 16 on p. 406) reporting that most rows by Schoenberg's student Anton Webern were anti-tonal as well, while the rows of Berg were more equivocal. Huron's presentation of results was very terse, however, and gave little detail regarding how these results were obtained.
In this article, we fill in the missing details, describing the data that were used, how the concept of anti-tonality (or "contra-tonality") was operationalized, what other common characteristics of Viennese twelve-tone rows were controlled, and how the statistical analysis was carried out. We also share data and code so that the analyses can be reproduced.
DATA
We used a publicly available database of 86 twelve-tone rows in the Humdrum kern format: 42 rows by Schoenberg, 21 by Webern, and 23 by Berg (London et al., 2002). The rows by Schoenberg were copied from an unpublished compilation assembled by Paul Metz in the early 1980s. The rows by Webern were encoded from those given in Kathryn Bailey's (1991) The Twelve-Note Music of Anton Webern. Rows by Berg were encoded from Dave Headlam's (1996) The Music of Alban Berg. The inclusion of some rows by Berg may be disputed. In his opera Lulu and his Lyric Suite, Berg used several tone rows that are only slightly different from each other; in his opera Wozzeck and his Chamber Concerto, which predate his adoption of Schoenberg's method, he used twelve-tone "themes" that he did not use the way he would later use tone rows (Headlam, 1996). If our sample of Berg's music were larger, we might have excluded some of these debatable examples. As the sample is small, though, we chose to include them all. Even so, statistical power was limited.
For comparison, we simulated 1,000 tone rows by putting the 12 chroma in a random order. Comparing the random tone rows to the composed tone rows allowed us to test whether the tonal fit of the composed rows was lower or higher than would be expected by chance.
METHODS
Operationalizing Tonal Fit
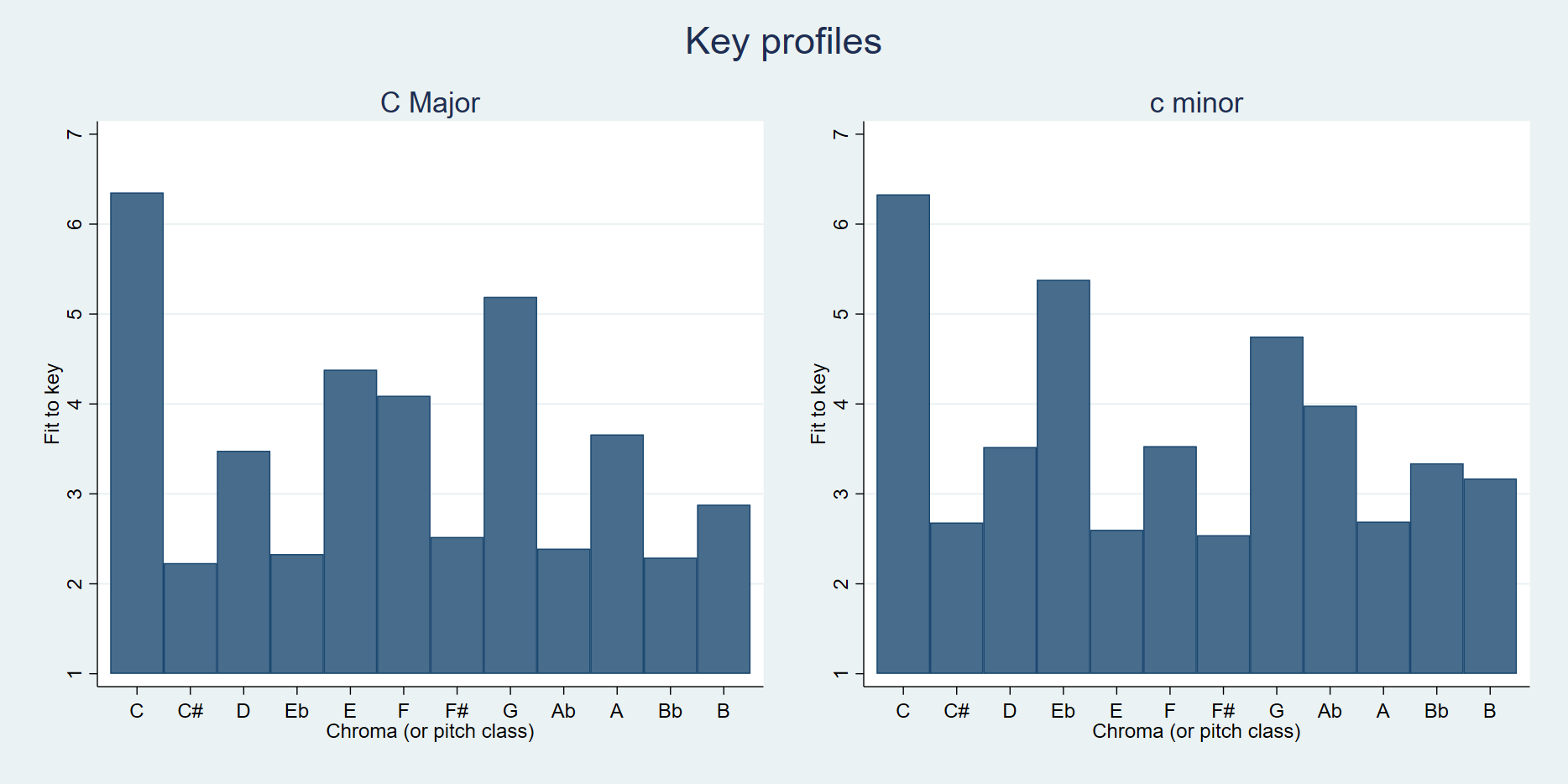
We estimated the degree to which each tone row evoked listeners' tonal schemata. To do so, we used the key-finding algorithm of Krumhansl and Schmuckler (KS) (Krumhansl, 1990; Krumhansl & Schmuckler, 1986), which estimates the key of musical material by correlating its pitch distribution with prototypical major and minor "profiles" representing the average score (on a scale from 1 to 7) that listeners gave to a heard pitch when asked how well it fit a key evoked by an opening cadence. Figure 2 presents the major and minor profiles, depicted using the keys of C Major and C Minor. The key profile with the highest correlation to a sample of musical material is estimated to give "the key" of the material. The strength of the correlation is a measure of how well the material fits the key.
We hypothesized that most twelve-tone rows by Schoenberg and Webern would have lower-than-chance correlations with even the best-fitting KS profile. Of course, the full twelve-tone row, because it uses all twelve chromas with equal frequency, will have an undefined correlation with the profiles. So instead we estimate the correlations between the profiles and different segments containing n < 12 consecutive tones from the rows. In particular, we estimate how well the profiles correlate with a row's first two tones, its first three tones, its first four tones, and so on up to its first eleven tones. Then we apply the same procedure to the row's retrograde, its inversion, and its retrograde inversion. The result is 44 correlations which we average together to estimate the average "tonal fit" of the tone row.
A few fine points are worth making. First, applying the correlations to the first n tones of the retrograde is equivalent to applying it to the last n tones of the original or prime row. Second, there was no need to transpose the row, since the correlations would be the same after transformation as before, except that the best-fitting key would be transposed. For example, if C Major was the best-fitting key for the prime row, with a correlation of 0.6, then C♯ Major would be the best-fitting key for the prime row when transposed up one semitone, and the correlation would still be 0.6. Finally, it is technically unnecessary to include eleven-tone segments. All eleven-tone segments are equivalent under some combination of transposition, retrograde, and inversion, so all have the same set of correlations with the KS profiles. Including the eleven-tone segments does no harm, however. If eleven-note segments were excluded, our measure of tonal fit would only change by a constant.
Control Variables
Past scholarship suggests that Schoenberg, Berg, and Webern had several other preferences that affected the structure of their tone rows. While it is not clear a priori whether these preferences would be correlated with a row's tonal fit, it is important to control for these other preferences when estimating whether the tonal fit of their rows is above or below chance.
As noted in the introduction, all three composers sometimes used twelve-tone rows that could be "derived" from shorter segments of two, three, four, or six notes, where the segments were related by transposition, inversion, or retrograde (Babbitt, 1955). We coded a dummy variable that was 1 for derived rows and 0 for rows that were not derived.
Another row type is a row whose first six chromas, when inverted and transposed by some number of semitones, become their own complement—that is, they become the remaining six chromas of the chromatic scale, in any order. This is known as inversional hexachordal combinatoriality (IHC) (Babbitt, 1955). An IHC row is not necessarily a derived row because there is no requirement that the last six tones of the row be in the same order as the transposed inversion of the first six tones. We coded a dummy variable that was 1 for IHC rows and 0 for rows that were not IHC (Babbitt, 1955).
Another type of row is a row with mirror symmetry, defined as a row that is its own transposed retrograde (a palindrome) or its own transposed retrograde inversion. In a broader definition of mirror symmetry, which we use here, we also allow row rotation (Hunter & von Hippel, 2003). We coded a dummy variable that was 1 for symmetric rows and 0 for rows that were not symmetric.
Webern is believed to have favored the interval of the semitone (half-step), at least before he adopted the twelve-tone method (Hanson, 1983). We therefore coded a variable representing the number of semitones in each row. Schoenberg and Webern are also believed to have preferred certain three-note segments, or trichords, notably the trichord 014 (e.g., C C♯ E and its transformations) and possibly the trichord 016 (e.g., C C♯ F♯ and its transformations) (Bailey, 1991; Haimo, 2006). We therefore coded two variables, one representing the number of 014 trichords and one representing the number of 016 trichords in each row. Nearly all rows had either 0 or 1 of these trichords; it was rare for a row to have more.
The first author recorded all these tone row features, including tonal fit, in a published database (London et al, 2002) so that the analyses here can be reproduced. It may be possible to identify additional characteristics that are thought to be more common than chance in Viennese twelve-tone rows. Statistically, however, there is a limit on how many variables we can control, since the number of variables in a model should not be too large relative to the number of cases, and there are relatively few Viennese rows (42 by Schoenberg, 21 by Webern, and 23 by Berg).
Models
We first compared the tonal fit of the random rows to the composed rows by Berg, Webern, and Schoenberg. We compared the mean tonal fit using linear regression with robust standard errors. We also used quantile regression to compare the median tonal fit in the same way.
We then checked whether the tonal fit discriminated between random and composed rows when other row characteristics were controlled. We did this using a logistic regression model that predicted the odds of whether a row was composed, rather than random, using the tonal fit (standardized for interpretability), indicators for whether the row was derived, IHC, or had mirror symmetry, and counts of the rows semitones, 014 trichords, and 016 trichords. We fit the logistic regression separately to rows by Schoenberg, Webern, and Berg. Each logistic regression included the same comparison set of 1,000 random tone rows.
RESULTS
Figure 3 gives violin plots summarizing the distribution of tonal fit within and between the random rows and the rows by Berg, Schoenberg, and Webern. On average, the tonal fit is significantly lower in Schoenberg and Webern than in the random rows (both ps < .01). Average tonal fit is higher in Berg than in the random rows, but not significantly higher (p = .60). Notice, however, that the distribution of tonal fit is asymmetric in Berg, so that the median, indicated by the white dot, is notably higher than the mean. In fact, the median tonal fit of Berg's tone rows exceeds the median tonal fit of the random rows by an amount that is borderline significant (p = .08). The median tonal fit of Schoenberg and Webern's rows is significantly lower than the median tonal fit of the random rows (p < .01 for Schoenberg, p < .01 for Webern).
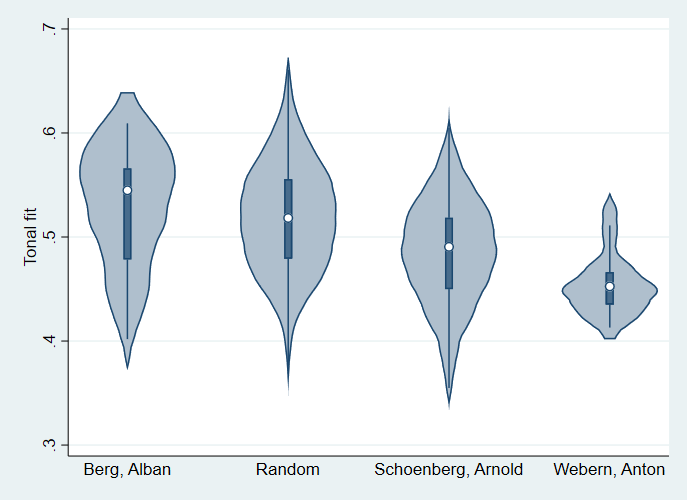
Figure 3. Violin plots of tonal fit. Each violin gives the shape of the distribution, smoothed using kernel density estimation. Inside each violin is a conventional box plot giving the median (white dot), interquartile range (box), and upper and lower adjacent values (whiskers).
As a check for face validity, we examined the fifteen composed rows with a tonal fit greater than 0.55, which corresponds to the top quartile of the random rows. Ten of these highly tonal rows were by Berg, including the Violin Concerto (whose row we gave in Figure 1), seven rows from the opera Lulu, the row from the concert aria Der Wein (The Wine), and a row from the Lyric Suite for string quartet, also used in Berg's 1925 setting of "Schliesse mir die Augen beide" ("Close both your eyes for me"). Berg is widely recognized to have used rows with tonal implications (Headlam, 1996). The other five rows with a strong tonal fit were by Schoenberg; three of these were works for a capella chorus, where Schoenberg may have used more tonal language to make the singers' job easier. None of the most tonal rows were by Webern.
While the mean and median differences are suggestive, they are also potentially confounded by other differences between composed and random rows. Table 1 gives the prevalence of different row properties in composed and random rows. There are some clear differences.
| Row property | Schoenberg | Webern | Berg | Random |
|---|---|---|---|---|
| % mirror | 10% | 24% | 9% | 1% |
| % derived | 12% | 29% | 9% | 1% |
| % inversionally hexachordally combinatorial | 86% | 62% | 43% | 40% |
| Mean # semitones | 2.7 | 5.0 | 2.6 | 2.0 |
| Mean # 014 trichords | 0.9 | 1.6 | 0.3 | 0.4 |
| Mean # 016 trichords | 0.5 | 0.5 | 0.4 | 0.5 |
All three composers prominently used derived and mirror rows. This was especially true for Webern; about a quarter of his rows were derived, and a quarter were mirror-symmetric. Only about one-tenth of Schoenberg's and Berg's rows were derived or mirror symmetric, but this was still remarkable in comparison to the random rows, where only one percent were derived and one percent were mirror symmetric. It has previously been demonstrated that mirror symmetry is far more common in Viennese rows than would be expected by chance (cf. Hunter & von Hippel, 2003).
Two of the three composers had some preference for rows with the IHC property, but the property was not rare even in the random rows. Nearly nine-tenths of Schoenberg's rows and nearly two-thirds of Webern's had the IHC property. But only 43 % of Berg's rows had the IHC property, and this was comparable to the 40 % of the random rows that had the same property.
Webern made prominent use of semitones. His tone rows had an average of 5.0 semitones each, compared to 2.0 in the random rows. Schoenberg and Berg's penchant for semitones was much milder; they had only an average of 2.7 and 2.6 semitones per row, respectively—about a third more than the random rows.
Webern also had a strong predilection for the 014 trichord. His tone rows had an average of 1.6 such trichords each—four times more than the random tone rows. Schoenberg had a milder predilection, using about twice as many 014 trichords as the random rows. Berg evidently had no particular predilection for 014 trichords; he actually used slightly fewer such trichords than occurred by chance in the random rows.
Contrary to reputation, none of the composers displayed any prominent use of the 016 trichord in their rows. The number of such trichords per row was no higher in any of the composers' tone rows than it was in the random tone rows.
Because composers' other preferences might be correlated with the use of tonal or anti-tonal row structures, Table 2 controls for a variety of row features in logistic regressions predicting the odds of whether a row was composed rather than random. Separate logistic regressions were run for Schoenberg, Webern, and Berg, comparing the rows of each to the same comparison sample of 1,000 random tone rows. The results are summarized using odds ratios, which are the amount by which a predictor multiplies the odds of a row's being composed rather than random. In these data, with only 2 to 4 % of rows composed, multiplying the odds of being composed by a certain amount is approximately equivalent to multiplying the probability of being composed by the same amount.
When the logistic regressions control for other row properties, the results continue to suggest that Schoenberg and Webern, but not Berg, avoided rows with high tonal fit. For Schoenberg and Webern, the odds ratios associated with standardized tonal fit are significant and less than one, meaning that a high tonal fit reduces the odds of a row being composed. For Schoenberg, the odds ratio is 0.65, and for Webern it is 0.37. This means that, other variables held equal, a one standard deviation increase in tonal fit reduces by one-third the odds that the row is by Schoenberg rather than random, and reduces by two-thirds the odds that the row is by Webern and not random.
| Predictors | Composer | ||
|---|---|---|---|
| Schoenberg | Webern | Berg | |
| Tonal fit (standardized) | 0.65** | 0.37** | 1.33 |
| (0.12) | (0.17) | (0.31) | |
| Row is inversionally hexachordally combinatorial | 8.21*** | 1.02 | 1.00 |
| (3.78) | (0.63) | (0.44) | |
| Row is derived | 1.85 | 6.26 | 3.22 |
| (1.70) | (7.63) | (3.19) | |
| Row is mirror symmetric | 3.65 | 1.64 | 10.4** |
| (3.91) | (2.51) | (10.8) | |
| Number of semitones in row | 1.22* | 2.40*** | 1.66*** |
| (0.14) | (0.49) | (0.29) | |
| Number of 014 trichords | 1.81*** | 3.40*** | 0.44* |
| (0.36) | (1.13) | (0.19) | |
| Number of 016 trichords | 1.27 | 0.99 | 0.71 |
| (0.31) | (0.44) | (0.26) | |
| Constant | 0.0034*** | 0.00016*** | 0.0097*** |
| (0.0018) | (0.00016) | (0.0052) | |
| # composed rows | 42 | 21 | 23 |
| # random rows | 1,000 | 1,000 | 1,000 |
***p <.01, **p <.05, *p <.10.
For Berg, the odds ratio is greater than one, indicating that higher tonal fit increases the odds that a row is by Berg and not random. However, the odds ratio is not statistically significant. This is not too surprising since we have limited power and, even before we added control variables, the difference in tonal fit between Berg's rows and random rows was only borderline significant.
Although they are not the focus of our analysis, it is worth remarking which other predictors do and do not discriminate between random rows and rows by the three composers. Schoenberg clearly preferred rows with the IHC property, but the other composers did not, at least when their other preferences were controlled. The odds ratio indicates that a row being IHC increases about eightfold the odds that a row is by Schoenberg rather than random, but did not at all increase the odds that the row is by Webern or Berg.
It is not clear from the results whether any of the composers preferred derived rows. Being derived did not significantly increase the odds of a row's being composed, net of other predictors. Although the odds ratios associated with derived rows were quite high, they were not statistically significant because of large standard errors. The large standard errors come from the fact that the number of composed rows is small and the indicator for derived rows is moderately correlated (0.6) with the indicator for mirror symmetry.
Berg showed a clear penchant for mirror symmetric rows. Being mirror symmetric increases tenfold the odds of a row's being by Berg rather than being random. It does not significantly increase the odds of a row's being by Webern or Schoenberg. Again, the odds ratios are not small, but the standard errors are large because of the small number of composed rows and the correlation between a row's being mirror symmetric and being derived.
All three composers, but especially Webern, showed a significant preference for rows with a high number of semitones. For Webern, each extra semitone more than doubled the odds that a row was by him rather than random. For Berg, the preference for semitones was a little weaker, and for Schoenberg it was still weaker, but still significant. On reading this article, Niels Chr. Hansen pointed out that the preference for semitones "is quite interesting given the characterization of the semitone as a 'rare interval' carrying 'critical information about local harmonic goals' in Butler's (1989) theory of 'intervallic rivalry.' In other words, it seems that Webern and Schoenberg composed in an anti-tonal way yet prioritized semitone intervals."
Schoenberg and Webern also showed a predilection for the 014 trichord, but Berg showed a slight aversion. For Schoenberg and Webern, each additional 014 trichord approximately doubled or tripled the odds that a row was composed rather than random, but for Berg, each additional 014 trichord cut the odds by more than half.
None of the composers showed a statistically significant preference for the 016 trichord. This is somewhat surprising in light of previous scholarship, but not surprising in light of Table 1, which showed that, even without controlling for other preferences, 016 trichords were just as common in the random tone rows as they were in rows by any of the three composers.
CONCLUSION
Previous generations of music psychologists and psychologically oriented music critics sometimes faulted twelve-tone composers for ignoring listener psychology, and experiments have confirmed the difficulty of hearing certain structures important to twelve-tone composition (Albersheim, 1964; Gibson, 1993; Largent, 1972 for a review; Pedersen, 1975). Yet our results suggest that, in at least one respect, Schoenberg and Webern were excellent intuitive psychologists. They understood very well the cognitive challenge of writing anti-tonal music for tonally minded listeners. Recognizing the strength of listeners' tonal schemata, Schoenberg and Webern studiously avoided tonal implications in their tone rows, and this avoidance was still evident when their preferences for other row features were controlled. Berg, by contrast, did not avoid tonality and sometimes preferred rows that evoked a tonal response.
These findings may strike some readers as obvious or common sense. But not all readers will see them that way. Common sense sometimes turns out to be wrong, and even findings that confirm common sense need to be demonstrated with rigor. Huron (2006) presented the broad outline of our findings, but we have filled in in the details, so that the approach can be evaluated and the results can be reproduced.
ACKNOWLEDGEMENTS
This article was copyedited by Niels Christian Hansen and layout edited by Kelly Jakubowski.
NOTES
-
Correspondence can be addressed to Paul T. von Hippel, University of Texas, Austin, paulvonhippel@utexas.edu
Return to Text -
The inversion of the retrograde is the same as the retrograde of the inversion.
Return to Text -
Transposing a tone row up by t semitones is equivalent to transposing it down by 12-t semitones.
Return to Text -
Another complaint, originating with Schoenberg and later echoed by Milton Babbitt, was that the term atonal suggested music that did not have tones. The term atonal refers to a lack of tonic or tonality, and not of tones, but to someone unfamiliar with atonal music the term could sound misleading or disparaging.
Return to Text
REFERENCES
- Albersheim, G. (1964). Mind and matter in music. The Journal of Aesthetics and Art Criticism, 22(3), 289–294. https://doi.org/10.2307/427232
- Babbitt, M. (1955). Some aspects of twelve-tone composition. The Score and I.M.A. Magazine, 12, 53–62.
- Bailey, K. (1991). The twelve note music of Anton Webern: old forms in a new language. Cambridge University Press. https://doi.org/10.1017/CBO9780511552458
- Bruner, C. L. (1984). The perception of contemporary pitch structures. Music Perception, 2(1), 25–39. https://doi.org/10.2307/40285280
- Butler, D. (1989). Describing the perception of tonality in music: a critique of the tonal hierarchy theory and a proposal for a theory of intervallic rivalry. Music Perception, 6(3), 219–241. https://doi.org/10.2307/40285588
- Gibson, D. (1993). The effects of pitch and pitch-class content on the aural perception of dissimilarity in complementary hexachords. Psychomusicology, 12(1), 58–72. https://doi.org/10.1037/h0094116
- Haimo, E. (2006). Schoenberg's transformation of musical language. Cambridge University Press.
- Hanson, R. (1983). Webern's chromatic organisation. Music Analysis, 2(2), 135–149. https://doi.org/10.2307/854246
- Headlam, D. J. (1996). The music of Alban Berg. Yale University Press.
- Hunter, D. J., & von Hippel, P. T. (2003). How rare is symmetry in musical 12-tone rows? The American Mathematical Monthly, 110(2), 124–132. https://doi.org/10.1080/00029890.2003.11919945
- Huron, D. (2001). What is a musical feature? Forte's analysis of Brahms's Opus 51, No. 1, revisited. Music Theory Online, 7(4).
- Huron, D. (2006). Sweet anticipation: music and the psychology of expectation. MIT Press. https://doi.org/10.7551/mitpress/6575.001.0001
- Krumhansl, C. L. (1990). Cognitive foundations of musical pitch (First edition). Oxford University Press.
- Krumhansl, C. L., Sandell, G. J., & Sergeant, D. C. (1987). The perception of tone hierarchies and mirror forms in twelve-tone serial music. Music Perception, 5(1), 31–77. https://doi.org/10.2307/40285385
- Krumhansl, C. L., & Schmuckler, M. A. (1986). Key-finding in music: an algorithm based on pattern matching to tonal hierarchies. Paper presented at the 19th Annual Meeting of the Society of Mathematical Psychology, Cambridge, MA.
- de Lannoy, C. (1972). Detection and discrimination of dodecaphonic series. Journal of New Music Research, 1(1). https://doi.org/10.1080/09298217208570157
- Largent, E. J. (1972). An investigation into the perceptibility of twelve-tone rows (Doctoral dissertation, The Ohio State University, Columbus, OH). Retrieved from https://etd.ohiolink.edu/!etd.send_file?accession=osu1486736926719883&disposition=inline
- London, J., von Hippel, P. T., Huron, D., Cartano, J., Kingery, K., Olsen, B., & Santelli, T. (2002, June 24). Row forms in the serial works of Schoenberg, Berg, and Webern. Stanford, CA: Center for Computer Assisted Research in the Humanities. http://www.ccarh.org/publications/data/humdrum/tonerow/
- Miller, G. A. (1956). The magical number seven, plus or minus two: some limits on our capacity for processing information. Psychological Review, 63(2), 81–97. https://doi.org/10.1037/h0043158
- Morris, R. D., & Alegant, B. (1988). The even partitions in twelve-tone music. Music Theory Spectrum, 10, 74–101. https://doi.org/10.2307/745793
- Pedersen, P. (1975). The perception of octave equivalence in twelve-tone rows. Psychology of Music, 3(2), 3–8. https://doi.org/10.1177/030573567532001
- Piston, W., & Westergaard, P. (1968). Conversation with Walter Piston. Perspectives of New Music, 7(1), 3–17. https://doi.org/10.2307/832423
- Schoenberg, A. (1941/1950). Composition with twelve tones. In D. Newlin (Ed.), Style and Idea (pp. 214–245). Philosophical Library.
- Stravinsky, I. (1970). Poetics of music in the form of six lessons (Revised edition). Harvard University Press.
APPENDIX
Random tonerows generated for this study and Stata code used to prepare and analyze the data are available at: https://doi.org/10.18061/emr.v15i1-2.7655