Introduction
MAUCH, MacCallum, Levy and Leroi (2015) carried out a large-scale longitudinal study tracing changes in popular music in the United States over the half century between 1960 and 2010. For their study, they made use of a corpus consisting of recordings that reached the US Billboard Hot 100 charts during this time period. Of many musical changes, they found evidence of decreasing use of the dominant seventh chord, and increasing use of the minor-minor seventh chord. Their study relied on signal processing methods to analyze musical properties of audio files. Signal processing methods are especially valuable when investigating very large corpora; in the Mauch, et al. study, they analyzed some 17,000 audio recordings. While signal analysis methods have improved substantially in recent years, the accuracy of signal-based analysis can be problematic. In their experiment Mauch et al. used principal component analysis (PCA) to infer music theoretical information from clusters in the dataset. These clusters were then evaluated and assigned a "topic" (e.g. dominant seventh chord and minor-minor seventh chord). The current study proposes to carry out a replication of these two observations using a corpus of existing harmonic analyses of popular music instead of signal-based analysis. To anticipate our results, we will see that a method using independent expert judgments of harmony produces results that are consistent with the observations made by Mauch et al.
Hypotheses
Formally, we may state our hypotheses as follows:
H1. The use of dominant seventh chords in music popular in the United States declines over the latter half of the twentieth century.
H2. The use of minor-minor seventh chords in music popular in the United States increases over the latter half of the twentieth century.
Sample
For the purposes of this study, a convenience musical sample was employed by using data from the Billboard Data Set (Burgoyne, et al., 2011; Burgoyne, 2011), a collection of harmonic transcriptions of music that made the American Billboard Hot 100 charts between 1958 and 1991. The data set begins in 1958, the first year in which the Billboard Hot 100 charts appeared; the termination date of 1991 for the data set was chosen partly because Billboard changed their formula for computing charts in that year, but also because of the rising popularity of Hip-Hop during the 1990s, when harmonic diversity declines somewhat (Burgoyne, et al., 2011; p.634). The coded songs were randomly sampled across the time period.
Figure 1 reproduces Figure 1 from Burgoyne et al. (2011, p. 634) and details the sampling procedure used. The transcribing team consisted of some two dozen university-trained jazz musicians. Each song was harmonically annotated by two different coders; discrepancies in the analyses were reconciled by a third independent annotator. All of the transcriptions were coded in plain-text format and notated using a standardized approach described by Harte et al. (2005).
In summary, the Billboard Data Set provides a convenience musical sample appropriate for this replication study as its content and timespan resembles that of the corpus used by Mauch et al. (2015). Furthermore, it provides two important pieces of information pertinent to this study: (1) date of chart appearance for each popular song, and (2) roman-numeral analysis of the song's harmonic content.
Method
A key issue in characterizing the frequency of occurrence of a given chord relates to the use of musical repetition. Popular songs typically exhibit repeating cycles of harmonic progressions. These cycles may differ between the different sections of a piece (e.g., verse, chorus). In tallying the occurrences of a particular chord, musical repetition has the potential to greatly influence the frequency of a given chord. On the one hand, it might be suggested that each appearance of a chord represents a true occurrence of that chord. On the other hand, it might be suggested that repetition may unduly exaggerate a given chord. For the purposes of this study, the simple presence of a given chord in the song was tallied. While this procedure reduces sensitivity to the frequency of occurrence of a chord within a given song, it has the benefit of increasing the data independence. Accordingly, we will simply record whether a given song exhibits or does not exhibit the use of the chord of interest.
Apart from the issue of tallying the frequency of a given chord, there is the prior issue of deciding what counts as a particular chord. For example, in the case of dominant chords, there are many possible candidates. A difficult issue arises as to how to identify whether a given chord serves a dominant function. We can side-step this issue by focusing instead on the intervallic organization of the chord, rather than the chord's function.
Specifically, we will deem as a "dominant seventh" candidate any chord that exhibits a major third, a perfect fifth, and a minor seventh above the bass—or any permutation that would be consistent with a chord inversion. Notice that this may also include chords that feature additional tones. For example, a sonority with an added minor ninth could also be deemed a candidate chord. Henceforth, we will refer to these chords as major-minor sevenths rather than dominant sevenths.
Similarly, we will operationalize a "minor-minor seventh" candidate as any chord that exhibits a minor third, a perfect fifth, and a minor seventh above the bass—or any permutation that would be consistent with a chord inversion. Once again, a sonority with added tones (such as a minor ninth) could also be deemed a minor-minor seventh chord.
Given these operationalizations, a purpose-specific script was written to query the database. For each work in the database, three pieces of information were generated: the date of commercial release, whether or not the song contained a major-minor seventh sonority in its inventory of chords, and whether or not the song contained a minor-minor seventh sonority among its inventory of chords.
Results
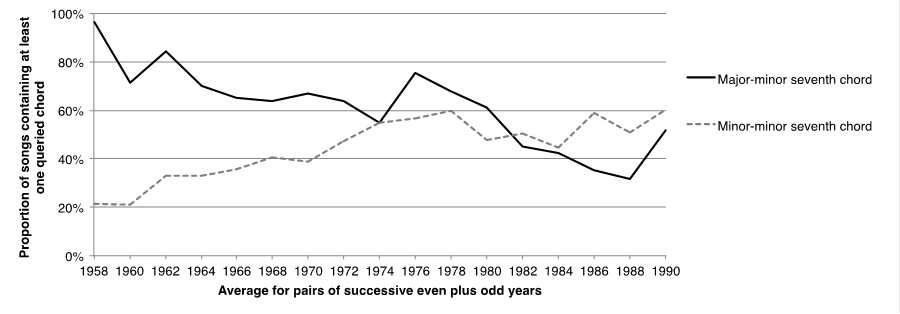
The results are summarized in Figure 2. The horizontal axis represents time, from 1958 to 1991. Rather than plot values for each successive year, plotted values represent averages for pairs of successive even plus odd years. The solid line represents the proportion of songs containing a major-minor seventh chord among its harmonic inventory. The dotted line represents the proportion of songs containing a minor-minor seventh chord among its harmonic inventory.
As can be observed, the solid line appears to decline over time, whereas the dotted line appears to increase over time. Calculating Pearson's r, the regression slope for the major-minor seventh data is -.77; with 32 degrees of freedom, this negative correlation is significant at the p<.01 confidence level. In the case of the minor-minor seventh data, the regression slope is .68 (df=32; p<.01). In short, the results are consistent with the two hypotheses motivating this study.

Figure 1. Sampling algorithm for the Billboard DataSet (reproduced from Burgoyne et al., 2011, Figure 1).
Discussion
Mauch, et al. (2015) have suggested that the declining use of major-minor seventh chords might be due to the declining popularity of jazz and blues artists. They further speculated that the increase in the use of minor-minor seventh chords appears between 1967 and 1977 and is attributable to the rise of funk, disco, and soul (Mauch, et al., Section 3.1, para. 2-3). Other accounts are certainly possible. For example, Schellenberg and von Scheve (2012) have observed a marked increase in the proportion of popular songs in the minor mode over this period. It may be that the minor mode facilitates the use of minor-minor seventh harmonies. The use of the major-minor seventh may be preserved in rock music, especially in the case of the mixolydian mode. At the same time, possible increasing use of dorian and aeolian modes may encourage the use of minor-minor seventh chords.
These changes in harmonic practices seem to extend beyond popular music. In a large longitudinal study examining the changes in 20th-century jazz harmonic practices, Broze and Shanahan (2013) found a similar decrease in frequency of major-minor seventh chords and increase in frequency of minor-minor seventh chords. Considering the findings presented by Mauch et al. (2015) and replicated here, it is possible that the changes in harmonic practices that occurred during the last century are not limited to a specific style or genre, or that changes in practices in a specific genre are affecting practices in other genres (e.g. the influence of rock on jazz practices during the late 60s and 70s, leading to the development of jazz-fusion). Further research is needed in order to better understand the reasons for these observed changes in late twentieth century music.
Conclusion
A replication study of Mauch, et al. (2015) was conducted focusing on two specific findings, the decreasing use of the major-minor seventh chord, and increasing use of the minor-minor seventh chord. While the original study was conducted using signal analysis to extrapolate musical properties from audio files, this paper aimed to replicate these findings using instead curated harmonic transcriptions. The results reported here are significant for two main reasons. First, they replicate the findings presented in the original study, tracing a change in harmonic vocabulary over the latter half of the twentieth century. Second, they reinforce the efficacy of using PCA of audio signals to extract information usually associated with music theoretical concepts such as harmony, information that traditionally needed to be evaluated by a human user.
NOTES
-
Email correspondence can be addressed to Hubert Léveillé Gauvin: leveillegauvin.1@osu.edu.
Return to Text
REFERENCES
- Broze, Y., & Shanahan, D. (2013). Diachronic changes in jazz harmony: A cognitive perspective. Music Perception: An Interdisciplinary Journal, 31(1), 32-45. http://dx.doi.org/10.1525/mp.2013.31.1.32
- Burgoyne, J.A. (2011). Stochastic processes and database-driven musicology. Unpublished doctoral dissertation, McGill University, Canada.
- Burgoyne, J.A., Wild, J., & Fujinaga, I. (2011). An expert ground-truth set for audio chord recognition and music analysis. In Proceedings of the 12th International Conference on Music Information Retrieval (pp. 633-38). Miami, FL. Retrieved from http://ismir2011.ismir.net/papers/OS8-1.pdf
- Harte, C.A., Sandler, M.B., Abdallah, S.A. & Gómez, E. (2005). Symbolic representation of musical chords: A proposed syntax for text annotations. In Proceedings of the 6thInternational Conference on Music Information Retrieval (pp. 66-71). London, England. Retrieved from http://ismir2005.ismir.net/proceedings/1080.pdf
- Mauch, M., MacCallum, R.M., Levy, M., & Leroi, A.M. (2015). The evolution of popular music: USA 1960-2010. Royal Society Open Science, 2(5), 150081. Retrieved from http://dx.doi.org/10.1098/rsos.150081
- Schellenberg, E.G., & von Scheve, C. (2012). Emotional cues in American popular music: Five decades of the top 40. Psychology of Aesthetics, Creativity, and the Arts, 6(3), 196-203. http://dx.doi.org/10.1037/a0028024