Introduction
TIMING analysis now comfortably out of its 'Western art music' shell, we find increasing evidence of non-metronomic rhythms across a range of musical traditions. In multiplayer performance, such rhythms give rise to attack offsets across parts (Keller, 2014), a feature of music-making often considered to be aesthetically pleasing (Gerischer, 2006; Stover, 2009) if not downright essential (Keil, 1987). This paper examines timing offsets in the context of Afro-Cuban ensemble drumming, a type of music recognized for its temporal complexity, auditory richness, and codified structures (Ortiz, 1950/1998).
Timing analyses of African and African-diasporic multiplayer percussion music have tended to focus on the 'horizontal' dimension, showing how various ostinatos depart from a grid of equidistant metrical subdivisions. To my knowledge, Kubik (1965) is the earliest example of such data-driven analysis. Using 8mm video, he captured the kinetic properties of xylophone duet performances in northern Mozambique, then relied on frame-by-frame transcription to produce accurate scores. More recently, Polak (2010) and Polak and London (2014) have shown that Malian drumming departs markedly and in consistent ways from an even subdivision grid. In regard to Afro-Cuban drumming, Alén (1995) examined timing trends in four different Tumba Francesa toques (interlocking grooves). Each of the 10 ostinatos he analyzed (two or three per toque) featured a consistently ungridded temporal contour.
Bilmes (1993) examined data he collected from four percussion instruments in Cuban rumba recordings made at MIT by Los Muñequitos de Matanzas. Bilmes's analyses focused mainly on how the three congas' attack times differed from an abstract referent grid derived from the gua-gua player; these differences were widespread as well as phrase-dependent, with similar phrases having similar timing contours. Even though it may be inferred that the rhythms in the above studies do not always line up with each other in absolute simultaneity, offset magnitudes between players are not reported.
The 'vertical' dimension of ensemble percussion is explored in Gerischer (2006). In her analysis of Brazilian samba from Salvador de Bahia, Gerischer notes that "simultaneous accents with slightly different timing produced on different percussion instruments result in flams …. These flams do not appear to disturb the flow of the acoustical events but rather contribute significantly to the creation of groove" (p. 111). Approximate offset values can be made out visually from the millisecond locations of subdivision tick marks in Gerischer's Figs. 5 and 6. Although specific values are not provided, the magnitudes do not appear to be trivial. Also studying samba, Lindsay and Nordquist (2007) found recurring offsets of about 15 ms between the pandeiro and tamborim parts in a duet recording. Turning to Cuban music, we find samples of interplayer offsets in Washburne (1998), whose visual assessment of spectrograms revealed consistent anticipations and delays among five percussion instruments (as well as piano and bass) in a commercial recording of salsa.
To date, Stover (2009) offers the most in-depth analysis of rhythmic counterpoint in Afro-Cuban music. My primary goal is to investigate what Stover calls a "friction between rhythmic strata that do not line up precisely (with an actual or imagined metric grid, or with one another)" (p. 110). Keil (1987) believed this friction—the so-called participatory discrepancies he found so prevalent in African-American music—to be a staple of "socially valuable" music (p. 275), while Chernoff (1979) noted that in African drumming "one rhythm defines another by crossing and cutting it" (p. 97). Their remarks resonate with Wilson's (1974) observation that Africa-derived music tends to "fill up every available area of musical space" (p. 15).
Drawing on multitrack recordings made in Cuba specifically for the purpose of timing analysis, I provide quantitative support for the idea that Afro-Cuban ensemble drumming involves frequent attack offsets across parts.
The Corpus
The analyses are derived from a collection of multitrack recordings made by Andrew McGraw during a research trip to Santiago de Cuba in May 2014. Led by Maestro Blas, the five musicians featured in the recordings are highly seasoned professional percussionists who perform regularly at secular and religious gatherings in and around Santiago. They were acquainted with the aims of this project and they received payment for their performances. The musicians themselves designed the content of the recording session, which ended with a brief interview.
The audio was captured using custom piezo sensors attached to each instrument with gaffers tape. The lines were run into a pre-amp and then into separate channels of a JoeCo 24 channel hard disk field recorder at 96000 Hz. This setup did not in any way modify the drummers' playing technique. I imported the individual tracks into Sonic Visualizer, then took interonset measurements using the Aubio Onset Detector plugin. All onset markers were checked manually and corrected as needed, ensuring accuracy to within ±1ms in most instances.
The recording session included seven distinct performances: a Tumba Francesa (of which only the first toque, Masón, is considered here), three types of rumba (Yambú, Guaguancó, Columbia), and three selections of Haitian origin (Yambalú, Nago, Bodu). 2 Performances varied in tempo and consisted of either four or five percussionists. Table 1 provides a summary of each performance; basic transcriptions appear in the Appendix.
| Masón | Yambú | Guaguancó | Columbia | Yambalú | Nago | Bodu | |
|---|---|---|---|---|---|---|---|
| players | 5 | 5 | 5 | 5 | 4 | 4 | 4 |
| duration (m:s) | 2:50 | 5:00 | 5:12 | 3:13 | 2:08 | 2:36 | 2:26 |
| tempo (bpm) | 126 - 134 | 72 - 84 | ~ 142 | 105 - 171 | 103 - 111 | 158 - 168 | 182 - 195 |
| total bars | 94 | 101 | 186 | 121 | 58 | 105 | 114 |
| total onsets | 3,620 | 5,365 | 6,544 | 5,278 | 1,824 | 3,418 | 3,606 |
Near-Unisons
Deviation, asynchrony, and discrepancy are terms commonly used in discussions of musical timing. While useful in certain contexts, in the present case these terms can connote at best an evasion of normative musical behavior and at worst an absence of coordination and common purpose. I opt for the more neutral term offset to refer to cases where two non-simultaneous attacks lie relatively close together in time. 3 We are interested in those offsets that are large enough to allow each attack to either sound independently or contribute a dose of fuzziness; too much proximity and the two attacks are likely to fuse. Determining such a threshold is no straightforward matter, however. Listener placement undoubtedly plays a role (Anku, 1997), as do timbre and amplitude, with similar sounds probably requiring smaller offsets in order to achieve attack separation (Sandell, 1995). A player's function within the ensemble is also relevant: as Butterfield (2007) has suggested, offsets are likely to be smaller between parts holding up a rhythmic groove than between parts in a melody-accompaniment pairing.
In this article I set the minimum offset threshold at 20 milliseconds. Two closely adjacent attacks at or above that threshold form what I call a near-unison, while a pair of attacks within the threshold—if their unsigned offset is between 0 and 19 ms—is considered to form a unison proper. Of course, in reality there is no such rigid boundary between rhythmic fusion and separation, since two perceptually distinct onsets lying 20 ms apart would not suddenly fuse into a single auditory event if they were nudged closer by 1 ms. But this reality is outweighed by the computational advantage of working with a clear cutoff point.
Why 20 ms? Hirsch (1959) gives a threshold of 2 ms, a figure that may hold for isolated sine tones in the lab but seems unrealistic for most musical contexts. Through informal measurements of flams across percussion instruments in this corpus and elsewhere, I found that the separation becomes noticeable when the offset is at least 10 ms. I doubled that value in order to ensure that the effect being studied is perceivable without great attentional effort, especially in cases where timbre and amplitude differences would require greater temporal separation.
As an introduction to near-unisons, consider the timing data displayed in Figure 1. Points correspond to interonset intervals in the composite rhythm formed by collapsing Masón's five instrumental parts—in other words, by merging the five time series (each containing a list of attack times) into one meta-series. 4
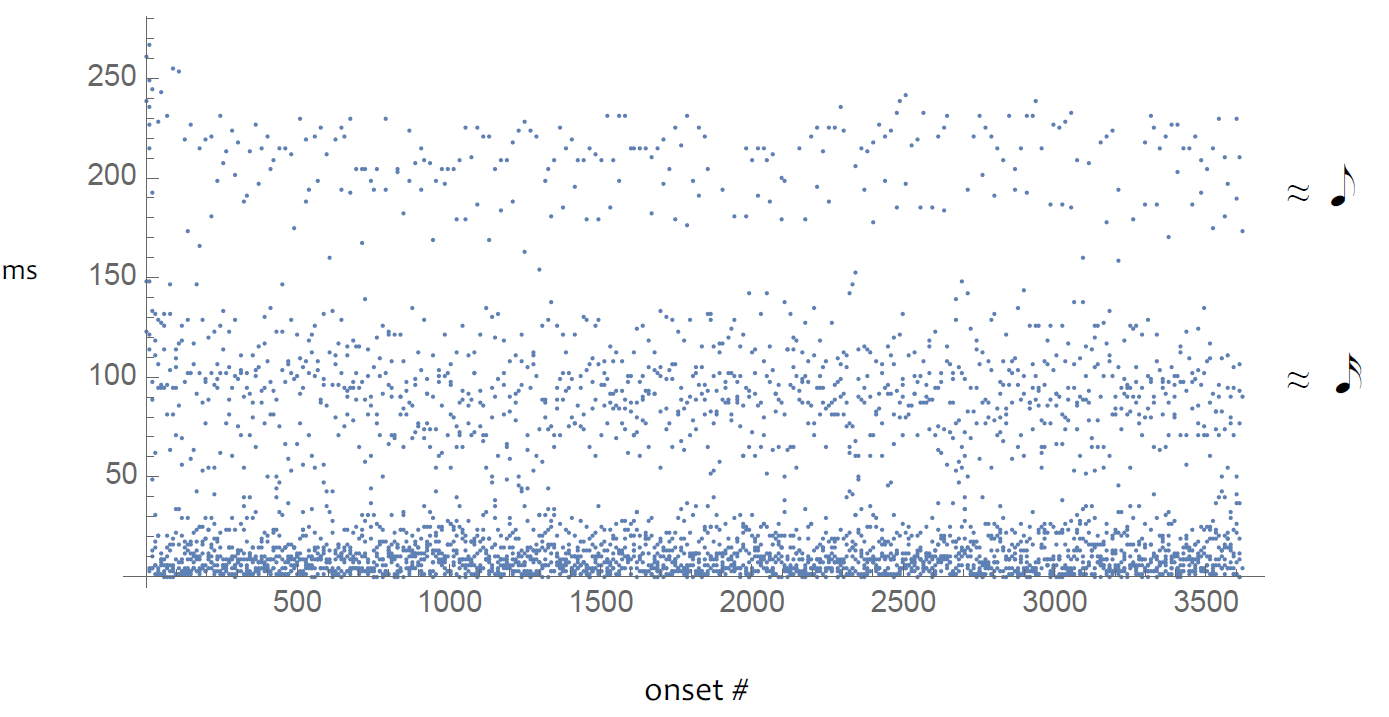
Fig. 1. Interonset intervals in the composite rhythm formed by merging Masón's five instrumental parts. Approximate metronomic durations for the eighth-note and sixteenth-note are shown on the right.
Three main strands are visible, corresponding to the eighth-note (top), sixteenth-note (middle), and rhythmic unison (bottom). The pervasive variability within each strand attests to the non-metronomic nature of the individual parts. Focus on the whitish region that lies between the two bottom strands, roughly between 20 and 80 ms. There is a reason why this region looks sparse: it contains only those durations that are either too fast to cohere metrically (< ~85 ms) or too large to form a solid unison (> ~15 ms). 5 Sparse does not mean empty, however. The graph contains 677 points in the 20-80 ms region, or 19% of the total number of onsets in the performance. Roughly one in five pairs of adjacent attacks in Masón's composite rhythm forms a near-unison.
The overall proportion of near-unisons in Yambú (15%), Columbia (20%), and Bodu (18%) is roughly the same as in Masón, while it is greater in Guaguancó (25%) and much lower in Yambalú and Nago (both 6%). With these last two exceptions, the preliminary data support the impression that near-unisons are prevalent in the corpus and, by extension, in Afro-Cuban ensemble drumming.
Merging all parts into a performance-length composite rhythm and calculating differences between adjacent attack times—as above—gives a useful initial representation of ensemble offset activity over time. However, this method ignores potentially meaningful connections between non-adjacent attacks (second-order differences and higher). Figure 2 shows a narrow time window containing five hypothetical attacks, one per player. Applying the above method to this situation yields no near-unisons, since all interonset intervals are below the 20 ms threshold. Qualitatively, this interpretation is disputable because it amounts to clumping the five attacks into a unison. I would argue that the potential to hear (for example) player 1 and player 2 as a near-unison should not be automatically invalidated by player 4's intervening attack. Therefore the next step in the analysis requires that we consider subsets of the ensemble, beginning with the timing characteristics of individual parts and continuing with the association between specific pairs of players.
The Ostinatos, Alone and In Combination
Each of the performances contains either two or three layered ostinatos, as well as a lead conga and at least one 'running' part that sounds—often with accentual differentiation—all 12 or 16 metrical subdivisions in the cycle. The ostinato cycles have the same length (they are not polymetric) and feature limited or no rhythmic variation throughout the performance. In this section I examine the timing contours of different ostinatos to gain a sense of their individual makeup as well as their rhythmic compatibility.
Performances based on the standard pattern: Yambalú, Nago, Bodu, and Columbia
Much has been written about the central role of the 'standard pattern,' the seven-stroke ostinato that underpins much African and African-diasporic music (see Agawu, 2006 for an overview). The pattern consists of five long (L) and two short (S) durations, forming the sequence L-L-S-L-L-L-S (usually notated with quarter-notes and eighth-notes). The pattern appears in all four of the 12/8 performances in the corpus: one rumba (Columbia) and the three Haitian dances (Yambalú, Nago, and Bodu); it is always played on the bell. Figure 3 gives their normalized note durations.
Within each dataset, there is clear differentiation among the five long notes as well as between the two short notes; these timing tendencies are shared by the four graphs. 6 The two most salient shared tendencies are the short-long contrast between the first two quarter-notes, and the reduction of durational contrast (a.k.a. assimilation) between the last (shortened) quarter and last (lengthened) eighth. This confirms that the pattern, which is played by the same musician in the four recordings, cannot be fully represented with the metronomic subdivisions of a 12/8 grid.
With the ensemble's core pattern tracing an 'off-the-grid' contour, any added layer that is played deadpan (at least in part) or with a 'personalized' contour that differs from the bell's will give rise to cross-player offsets. Even if the timing contour were the same in both parts, a slightly out-of-phase alignment would result in offsets as well. We will encounter both of these situations next.
In two of the Haitian selections (Yambalú and Bodu), the bell pattern is doubled in rhythmic unison by one of the congas. To differentiate between the foundational part and its clone, I will refer to them as the bell and the double. Our first order of business is to determine the size of the offsets created when bell and double are combined. Figure 4 shows side-by-side timings for the bell (reproduced from Fig. 3) and double in Yambalú and Bodu. 7 There are visible differences in the Yambalú graph; for instance, the two quarter-eighth sequences (notes 2 and 3, then 6 and 7) are more evened out in the double part (blue) than in the bell (amber). In Bodu, the two instruments' timing contours appear almost identical. 8 Despite this fundamental difference between the two performances' mode of alignment, we will see that near-unisons are present in both.

Fig. 3 Normalized timing contours of the standard pattern. Each interonset interval is divided by the total bar duration that contains it to yield a scaled value between 0 and 1. Horizontal dashed lines mark deadpan values.
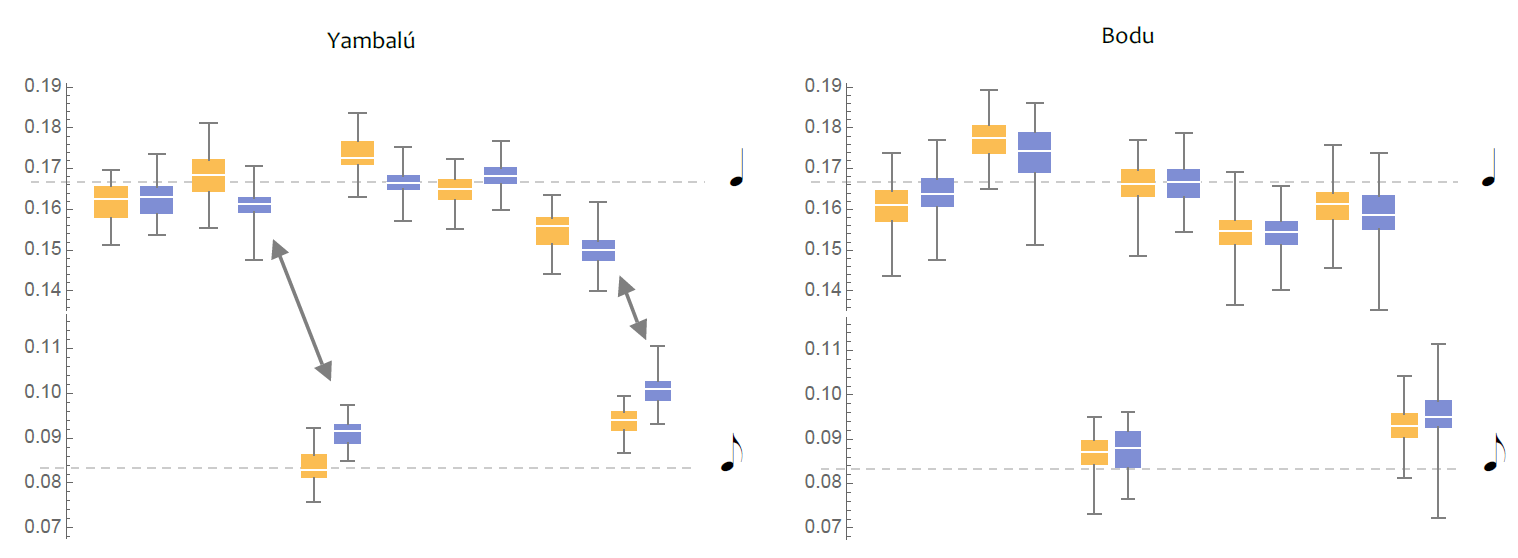
Fig. 4. Normalized timing contours for the bell (amber) and conga double (blue) versions of the standard pattern. Double arrows point to evened out durations.
In order to determine whether any vertical timing differences between the bell and double are anything but perceptually negligible jitter, we switch the measurement unit from scaled to absolute durations.
Figure 5 shows the distribution of offset sizes for every pair of corresponding notes across the two parts in each performance. Yambalú's normal curve around zero indicates an abundance of attack pairs that are close enough to fuse. But the histogram also contains a considerable quantity of near-unisons: 17% of offsets are 20 ms or more (in either direction). 9 Interpreting the Yambalú data another way, we find that 70% of bars contain at least one near-unison between bell and double, and 35% contain at least two.
The Bodu distribution is also normal but it is centered around 10 ms, indicating that one part tends to lag behind the other—the two parts are slightly out of phase. 10 There are fewer near-unisons here than in Yambalú, but still an appreciable amount: 14% of Bodu's offsets between bell and double lie in the near-unison range, with 58% of bars containing at least one near-unison and 27% containing at least two. These figures suggest that non-simultaneous attacks are integral to the contrapuntal skeleton of both performances, even though the two ostinatos forming the skeleton follow the same fundamental pattern. 11
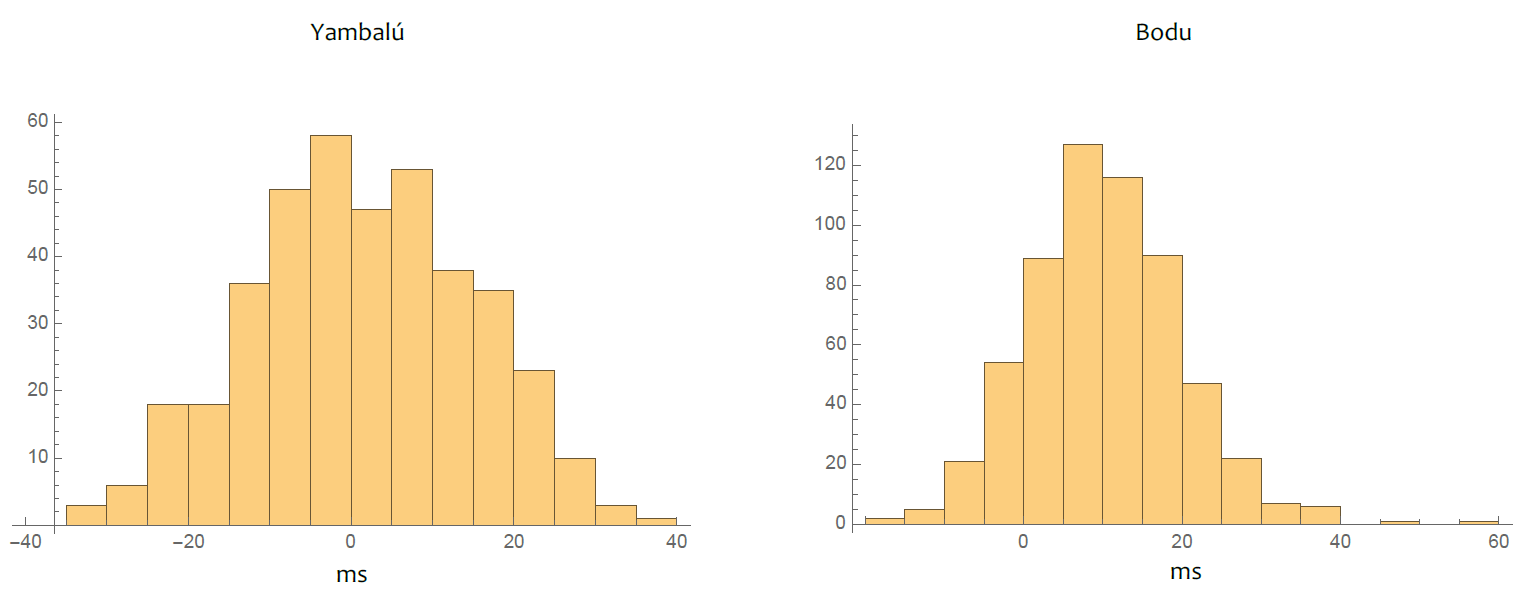
Fig. 5. Distribution of offset magnitudes between bell and double standard patterns in two Haitian selections. (Note that the y-axes have unequal scales.)
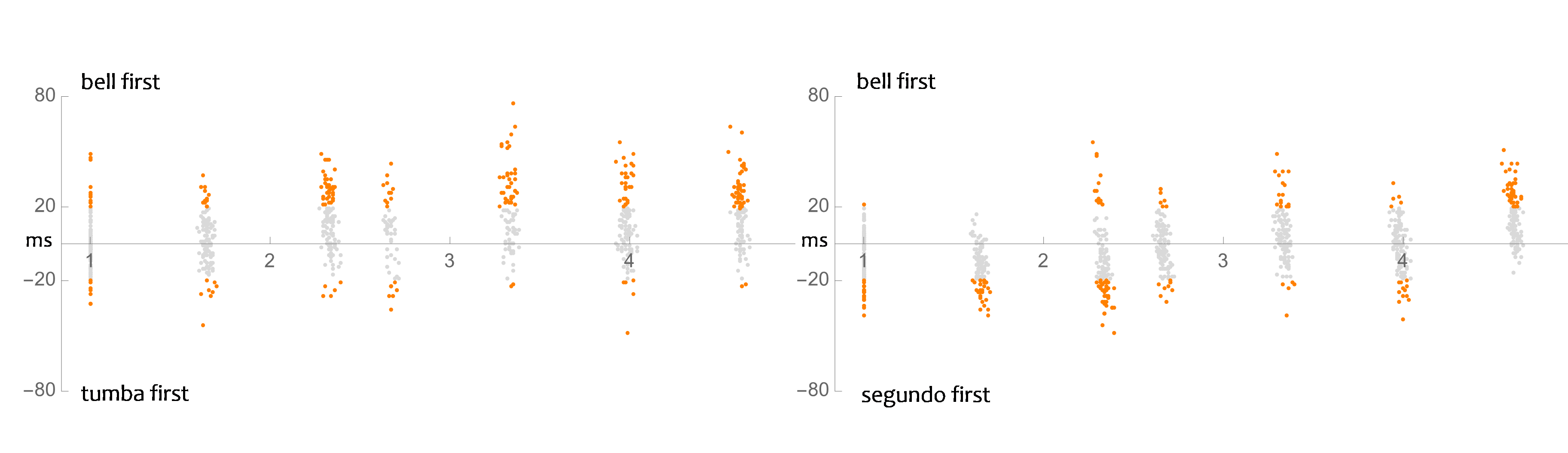
We now turn to Columbia's standard pattern, which is played against the eight-stroke palito. Figure 6 shows offset magnitudes for the six points of convergence between the two parts. Near-unisons are plotted in orange. The x-axis corresponds to the normalized location of the bell's attack within the bar. The bell is ahead of the palito four out of six times; the effect is especially robust during the second half of the cycle. The high incidence of near-unisons in that region of the bar is worth noting: the two instruments produce near-unisons 78% of the time, about four times as often as on the downbeat. 12 Force of analytical habit tempts us to see these offsets as arising from 'rushing' or 'laying back.' While the musicians may be rushing or lagging with respect to each other, I caution against emphasizing dependence on an abstract and isochronous tactus—a tactus that may or may not form part of the musician's conception of time at various points in the performance. The shaping of the patterns is guided by a combination of factors that include musico-cultural tradition, kinematic preferences, stroke resonance, individual musical aesthetics, deep familiarity with the associated dance, and a conception of how each part fits within the fabric of the whole ensemble.

Fig. 6. Columbia offsets between bell and palito. Orange points denote near-unisons. The (abstract) locations of beats 1-4 (in a 12/8 hearing) are given as reference.
Figure 7 plots pairings between Columbia's bell and the two conga 'running' parts. The bell is mostly ahead of the tumba (low conga), as was the case with the bell-palito pairing, while the bell-segundo (mid conga) pairing reveals a fairly even lead/lag distribution between the two parts. We can glean from these offset graphs—including the one in Fig. 6—that some of the bell's strokes are consistently ahead of the other parts, while other bell strokes show no such consistency. An example of the former case is the bell's last stroke, which is almost always ahead as a result of the evened out long-short pair at the end of the standard pattern, as discussed above. 13 For an example of inconsistently signed bell offsets, we can point to the end of beat 1, where the bell is ahead with respect to the palito, behind with respect to the segundo, and a bit of both with respect to the tumba. The network of cross-player offsets is a combination of fixed and fluid relationships.
Performances based on the rumba clave: Yambú and Guaguancó
A staple of Afro-Cuban music, the rumba clave pattern appears in two of the rumba performances in the corpus: Yambú and Guaguancó. In both of these performances, the clave pattern is also heard embedded in the cascara, a 10-stroke pattern played on the gua-gua. 14
In Yambú, the clave pattern is slightly modified: in addition to sounding the five notes of the rumba clave, it adds strokes on the two beats that are typically left silent (beats 2 and 3). 15 The Yambú clave and cascara share onsets in six regions of the bar, corresponding to the downbeat, the end of beats 1 and 2, the start and midpoint of beat 3, and the start of beat 4. The clave's two pairs of long-short durations in the first two beats are 'swung.' With mean ratios of 2.2 (first pair) and 2.3 (second pair), the long note is shorter than a dotted eighth-note but not as short as a quarter-note triplet, while the short note is longer than a sixteenth-note but not as long as a triplet eighth-note. These inflections lead to substantial offsets with respect to the cascara, which is played closer to an even sixteenth-note feel (though not strictly so). Figure 8 shows that these offsets (on the end of beats 1 and 2) are usually near-unisons, with the clave leading by 20 ms or more 75% of the time. The clave is also usually ahead of the cascara on the downbeat, but on the second half of the cycle (beats 3 and 4), the 'leader' and 'follower' roles are divided.
We see in Figure 9 how Yambú's clave and cascara line up individually with the lowest running part, played on tumba and cajon. As with the preceding offset graphs, near-unisons occur frequently, and leader/follower roles can be either evenly or unevenly distributed. In the left graph, the clave's 'swung' short notes (end of beats 1 and 2) are again ahead, in this case with respect to their counterparts in the tumba/cajon's sixteenth-note stream. Elsewhere in the cycle, it is the tumba/cajon that leads. In the right graph, the cascara lags through most of the cycle.
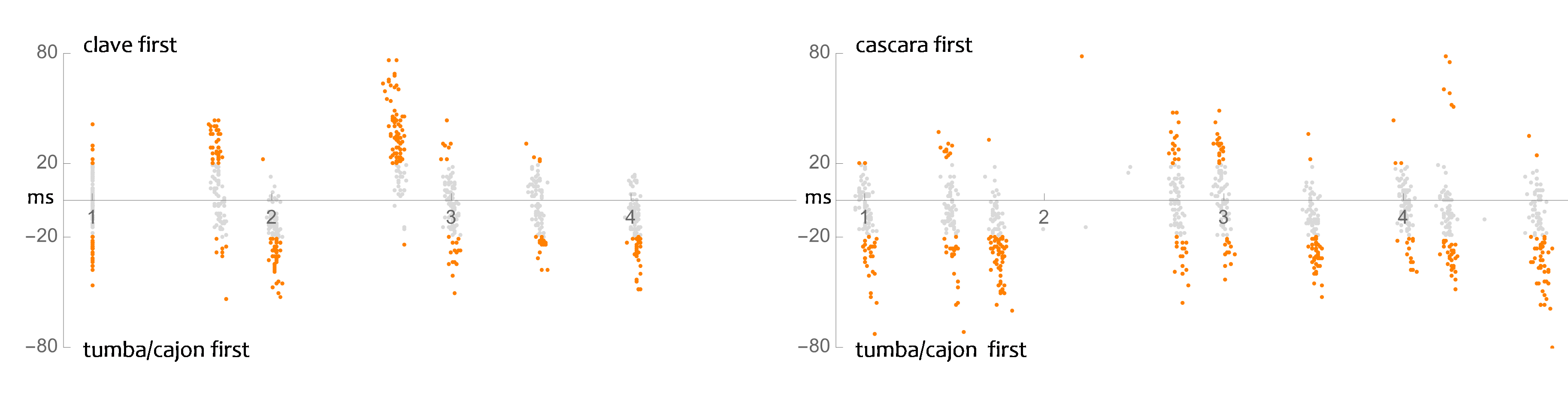
Fig. 9. Yambú offsets between clave and tumba/cajon (left), and between cascara and tumba/cajon (right).
Guaguancó is perhaps the most rhythmically complex performance in the corpus. Its core pattern (the rumba clave) is heard against not one but two other ostinatos: the cascara (as in Yambú) and what is sometimes referred to as tres golpes, played by the segundo. The quinto (lead conga) and a variably accented stream of triplets in the tumba complete the texture. In the transcriptions herein, the clave is notated with triplets while the cascara and segundo are notated with sixteenth-notes. If played as notated, the mere concurrence of triple- and quadruple-subdivision cycles would suffice to generate a rhythmic web of perpetual offsets. 16 Complex as that may be, the reality is drastically more so.
Each of the three Guaguancó ostinatos is played with a distinctive timing contour. As notated, the clave's first, third, and fourth notes have equal values. As performed, the first is on average 27 ms shorter than the third (285 ms vs. 312 ms) and 24 ms longer than the fourth (285 ms vs. 261 ms). Likewise, the second and fifth notes are notationally equivalent but differ on average by 21 ms (420 ms vs. 399 ms). These are not trivial amounts.
The cascara also resists isometric categorization. For instance, the short-long-short durations of its last beat are played with a mean ratio of .69:2.18:1.13 (rather than 1:2:1); the mean duration of the first short note is 70 ms, 35 ms (~30%) shorter than the deadpan value and well below the threshold for metrical subdivisions.
The segundo is equally idiosyncratic. Figure 10 examines its timing properties from two perspectives. Attack placement appears above the transcription. The x-axis corresponds to the scaled locations of onsets within the cycle (cycle length being determined from the clave's downbeats); vertical orange lines mark deadpan locations for reference. The (discrete) y-axis layers consecutive iterations of the ostinato from bottom to top. 17 The slanted gray lines highlight the fact that the segundo is consistently ahead of the gridlines. The fourth onset stands out as being particularly distant from its nominal location, being more closely aligned with beat 2 and thus a full sixteenth-note 'early.' (The second beat's notes are closer to a triplet starting on the beat than to a quadruple 'ee-and-uh,' as this pattern is commonly notated.)
Plotted below the segundo transcription in Figure 10 are mean interonset intervals, again scaled based on bar duration (as set by the clave). The horizontal dashed lines give deadpan coordinates for three different note values. Notice the deceleration arc that is first traced by the first four points and continues throughout the cycle (interrupted briefly by notes 5, 6, and 8). Notice also how note 7 (circled), whose duration lies roughly halfway between eighth and triplet, appears to act as a stepping stone within the ostinato's decelerating trajectory.
Superposed, Guaguancó's distinctively timed ostinatos create an abundance of near-unisons. Figure 11 aims the spotlight on every pairing between clave and cascara (blue), cascara and segundo (orange), and clave and segundo (green). For each pair, the proportion of near-unisons (offsets ≥ |20| ms ÷ total number of offsets) is displayed as a percentage. Regions of particular interest are the downbeat and the half-bar: the downbeat region features a transition from lower to higher values (19% to 39% and 41%), while the reverse happens at the half-bar region (56%, 37%, and 24% transition to 14%). Also noteworthy is the double cascara/segundo pairing on beat 2, where the segundo's earlier onset—recall note 4 in Fig. 10—results in 100% near-unisons with respect to the cascara's onset on the putatively equivalent position.
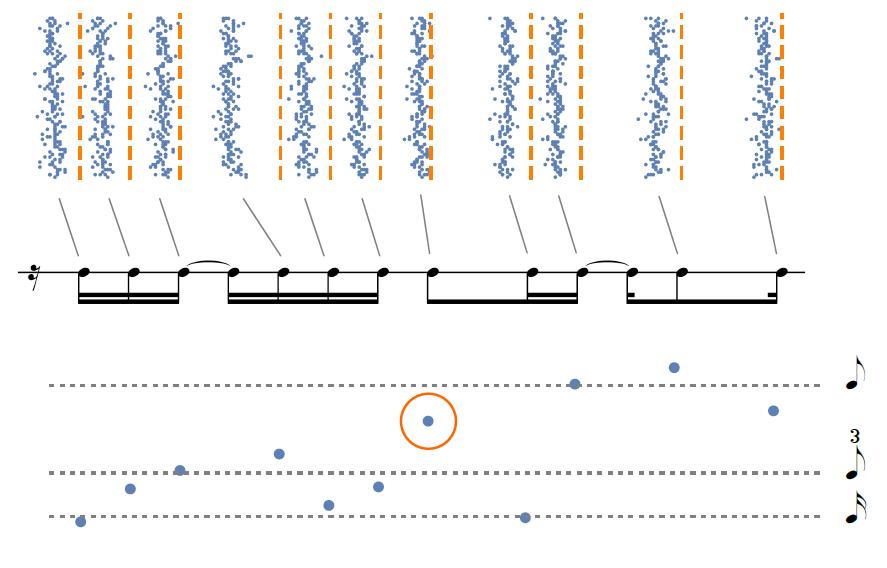
Fig. 10. Two (normalized) representations of Guaguancó's segundo timing: attack placement within the bar cycle (top graph) and mean interonset intervals (bottom graph).

Fig. 11. Proportions of near-unisons in matching attack pairs (top graph) and corresponding mean offsets (bottom graph). Positive values: clave first in clave/cascara (blue), cascara first in cascara/segundo (orange), segundo first in segundo/clave (green). All mean offsets are significantly different from zero at p < .0001 unless otherwise noted.
The lower graph in Figure 11 plots mean offsets for each of the three pair types. The clave appears to follow a sine-like trajectory with respect to the cascara (blue points): it is ahead of its partner at the beginning and end of the cycle, behind in the middle of the cycle, and closer to the 0 ms axis elsewhere. In contrast to this alternating relationship, the segundo consistently precedes the cascara (orange points). It is also worth noting that, while reasonably reflective of the performer's rhythmic feel, the clave's tripleted notation predicts the wrong offset sign on the three clave offbeats with respect to the quadruply subdivided parts. Whereas the end of beats 1 and 2 and the upbeat of beat 3 dictate that the clave should precede the cascara and segundo, generally the opposite happens.
Guaguancó's ostinato engine therefore features two types of consistent offset configurations from cycle to cycle: one where the cross-player ordering tends to remain the same (segundo and cascara), and one where the ordering tends to alternate in the same manner (clave and cascara). On top of these recurring relationships there is a freer, more stochastic dimension where orderings appear to fluctuate spontaneously. These three scenarios, which we also encountered along the way with the other dances, might form a useful framework for future analyses of ensemble interaction.
Afterthought: Onset Clusters
Having examined various pairwise combinations among parts, perhaps a logical afterthought is to consider onset clusters: near-simultaneous groups of two or more attacks across parts. 18
To identify clusters in the corpus, we first segment the merged composite rhythm of each performance (as in Fig. 1) by finding gaps greater than 80 ms between consecutive attack times. (The 80 ms buffer ensures that there is sufficient separation between clusters.) A cluster can contain no fewer than two elements. As sketched in Figure 12, this process results in a sequence of clusters of various widths and cardinalities. Unlike the above analyses, this approach takes into account timing data from the lead conga, whose rhythmic verve contributes in no small measure to the intricacy of the ensemble texture.
In fast non-metronomic performances, the high density of attack points can generate overly wide clusters with the same instrument represented two or three times. To avoid this, we introduce the condition that no player can appear more than once within a cluster. Clusters violating this condition are segmented recursively as needed until the condition is satisfied, so that the maximum possible number of elements in a cluster is the same as the total number of players in the performance. Finally, we categorize clusters according to their cardinality (number of attacks, or players) and calculate the interval between their endpoint attacks, or span. We will keep an eye out for clusters whose total span meets or exceeds the 20 ms threshold. A cluster meeting this criterion and containing two onsets is simply a near-unison.

Fig. 12. Schematic of the cluster-finding algorithm, which segments the 4- or 5-player composite rhythm into groups 80+ ms apart. Single elements are ignored.
Table 2 gives cluster statistics broken down by cardinality for the entire corpus. The two columns under each performance list cluster counts and span means in milliseconds. For instance, Masón's 994 clusters are 41 ms wide on average; 212 (21%) of these are three-player clusters, spanning 27 ms on average.
Scanning the bottom row indicates that grand span means exceed 20 ms in all performances except for Nago. As one might expect, cardinality and span are positively correlated: the more attacks in a cluster, the greater the span. (Also, quintet performances have greater spans than quartet performances. 19) In the case of quadruple and quintuple clusters, spans of 50 ms or more are common.
These figures suggest a high level of rhythmic density, especially in Masón and the three rumbas. To probe deeper, let us set (somewhat arbitrary) minimum span thresholds that are based on the 20 ms near-unison threshold and increase proportionally with cardinality, so that in order to be considered substantial, a cluster must span 20+ ms, 30+ ms, 40+ ms, or 50+ ms depending on whether it contains—respectively—two, three, four, or five elements. Using this metric, the average number of substantial clusters per beat in the quintet performances is 1.53. (The rate for the Haitian selections is .64.) The clusters follow each other in rapid succession—two to three times per second, depending on tempo—and thus help define the music's characteristically rich soundscape.
| Masón | Yambú | Guaguancó | Columbia | Yambalú | Nago | Bodu | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| # | n | ms span | n | ms span | n | ms span | n | ms span | n | ms span | n | ms span | n | ms span |
| 2 | 154 (.16) | 9 (8) | 315 (.21) | 18 (14) | 593 (.30) | 18 (19) | 176 (.12) | 20 (16) | 95 (.20) | 15 (11) | 364 (.32) | 11 (10) | 202 (.20) | 21 (23) |
| 3 | 212 (.21) | 27 (24) | 435 (.28) | 31 (19) | 766 (.39) | 39 (27) | 439 (.31) | 34 (26) | 162 (.33) | 19 (9) | 579 (.50) | 18 (14) | 376 (.37) | 30 (26) |
| 4 | 550 (.53) | 53 (35) | 601 (.39) | 34 (17) | 491 (.25) | 48 (30) | 606 (.42) | 37 (26) | 232 (.47) | 24 (11) | 210 (.18) | 25 (22) | 427 (.43) | 33 (27) |
| 5 | 78 (.08) | 57 (54) | 180 (.12) | 42 (18) | 131 (.07) | 66 (36) | 209 (.15) | 51 (34) | ||||||
| total | 994 | 1531 | 1981 | 1430 | 489 | 1153 | 1005 | |||||||
| mean | 41 (36) | 30 (19) | 37 (30) | 36 (28) | 21 (11) | 17 (15) | 29 (26) | |||||||
ACKNOWLEDGEMENTS
I am extremely grateful to Andrew McGraw for producing the recording sessions, generously sharing all the files with me, and answering all my questions about the performance process.
NOTES
-
Correspondence can be addressed to Fernando Benadon, fernando@american.edu.
Return to Text -
An eighth recorded performance—an abridged version of the Batá Oru Seco—will be explored in a separate article.
Return to Text -
This usage of the term "offset" is not to be confused with its other common usage, referring to the temporal endpoint of a sound (the opposite of onset). In this article, "onset" and "attack" are used interchangeably.
Return to Text -
For example, if onset locations (in seconds) along a timeline for players 1-5 are 1={.255, .490, …}, 2={.605, …}, 3={.515, …}, 4={.218, .521, .610, …}, 5={.517, .618, …}, then the merged composite rhythm = {.218, .255, .490, .515, .517, .521, .605, .610, .618, …}, and the interonset intervals are the differences between consecutive elements in the merged list.
Return to Text -
To avoid skewing the distribution of offset magnitudes, flams and rolls (occurring mainly in the lead conga) are excluded from Figure 1 and from all subsequent analyses.
Return to Text -
Four separate ANOVAs for the quarter-note (absolute) durations in each set are significant at p < .00001, with post-hoc Tukey tests showing highly significant differences between most pairs in each five-note group. Similarly, t-tests give significant differences (p < .0001) between eighth-note durations in each of the four sets.
Return to Text -
The double in Bodu occasionally varies the timeline pattern with additional notes. Its graph contains only those bars (n = 84) where the timeline pattern is intact.
Return to Text -
The second note's longer value in Bodu's bell and double has structural significance, as the double actually begins the cycle on this note—that is, the player's initial entrance happens on the slot corresponding to the bell pattern's second note (rather than on the bar downbeat). The double accentuates this secondary downbeat throughout the performance.
Return to Text -
Yambalú's bell and double are evenly split in terms of who leads and who lags. Mean ms offsets are significant for six of the seven note pairs in the L-L-S-L-L-L-S pattern: -4 (p < .01), -6 (p < .001), 9 (p < .0001), -8 (p < .0001), 7 (p < .0001), 0 (n.s.), and 10 (p < .0001); positive values denote a bell-first ordering. However, effect sizes are small, so statistical significance should not be automatically translated into perceptual relevance (Polak and London, 2014, footnotes 9 and 10).
Return to Text -
Mean ms offsets are significant at p < .0001 for all seven pairs in the pattern: 10, 6, 11, 9, 9, 9, and 13; positive values denote a bell-first ordering.
Return to Text -
Nago's bell is not doubled at the rhythmic unison. Instead, a 2-1-3 pattern in the tumba cycles twice per bar, coinciding with a bell onset only three times (the bell pattern's first, second, and sixth notes). These three alignment points form near-unisons 10% of the time; the low incidence is consistent with Nago's statistics reported above and elsewhere in the article.
Return to Text -
The palito contains a flam on the pattern's penultimate note. The graph in Fig. 6 incorporates the flam's first attack (notated as a grace note in the Appendix transcription) but not the second. If the flam's second note were considered instead of the first, the penultimate set of bell-palito offsets in the graph would display still higher values.
Return to Text -
The standard pattern contains two long-short pairs. In Columbia, the mean long-short ratio for the first pair of durations is a ternary 2.04, while the ratio for the second pair is a more evened out 1.65.
Return to Text -
Roughly one minute into the performance, Guaguancó's cascara switches from the 10-stroke version to the slightly different 11-stroke version. See Appendix.
Return to Text -
See Stover (2009, p. 294).
Return to Text -
Stover (2009) offers detailed discussions on how the layering of 12- and 16-cycles leads to offsets between instruments.
Return to Text -
The iterations (n = 167) are not strictly consecutive, given that the performer introduces a two-bar variant six times throughout the performance.
Return to Text -
The concept of onset clusters is closely related to Stover's (2009) beat span, the idea that a beat is "a scalable duration rather than a single instant in time," allowing for "microrhythmic clashes [to] exist in apparent cognitive consonance" (p. 163).
Return to Text -
Rasch (1988, p. 86) makes an analogous observation regarding "Western" classical ensembles.
Return to Text
REFERENCES
- Agawu, K. (2006). Structural analysis or cultural analysis? Competing perspectives on the 'standard pattern' of West African Rhythm. Journal of the American Musicological Society, 59(1), 1-46. https://doi.org/10.1525/jams.2006.59.1.1
- Alén, O. (1995). Rhythm as duration of sounds in Tumba Francesa. Ethnomusicology, 39(1), 55-71. https://doi.org/10.2307/852200
- Anku, W. (1997). Principles of rhythm integration in African drumming. Black Music Research Journal, 17(2), 211-238. https://doi.org/10.2307/779369
- Bilmes, J. (1993). Timing is of the essence: Perceptual and computational techniques for representing, learning, and reproducing expressive timing in percussive rhythm. Unpublished doctoral dissertation, Massachusetts Institute of Technology, USA.
- Butterfield, M. (2007). Response to Fernando Benadon. Music Theory Online, 13(1).
- Gerischer, C. (2006). O suingue baiano: Rhythmic Feeling and microrhythmic phenomena in Brazilian percussion. Ethnomusicology, 50(1), 99-119. http://www.jstor.org/stable/20174425
- Hirsch, I. (1959). Auditory perception of temporal order. Journal of the Acoustical Society of America, 31, 759. https://doi.org/10.1121/1.1907782
- Keil, C. (1987). Participatory discrepancies and the power of music. Cultural Anthropology, 2(3), 275-283. https://doi.org/10.1525/can.1987.2.3.02a00010
- Keller, P.E. (2014). Ensemble performance: Interpersonal alignment of musical expression. In D. Fabian, R. Timmers, & E. Schubert (Eds.), Expressiveness in music performance: Empirical approaches across styles and cultures (pp. 260-282). Oxford: Oxford University Press. https://doi.org/10.1093/acprof:oso/9780199659647.003.0015
- Kubik, G. (1965). Transcription of Mangwilo xylophone music from film strips. African Music, 3(4), 35-51. https://doi.org/10.21504/amj.v3i4.1064
- Lindsay, K., & Nordquist, P. (2007). Pulse and swing: Quantitative analysis of hierarchical structure in swing rhythm. The Journal of the Acoustical Society of America, 122, 2945-2946. https://doi.org/10.1121/1.2942485
- Ortiz, F. (1950/1998). La Africanía de la música folklórica de Cuba. Madrid: Editorial Música Mundana Maqueda.
- Rasch, R. (1988). Timing and synchronization in ensemble performance. In J. Sloboda (Ed.), Generative processes in music: The psychology of performance, improvisation, and composition (pp. 71-90). Oxford: Oxford University Press.
- Sandell, G. (1995). Roles of spectral centroid and other factors in determining 'blended' instrument pairings in orchestration. Music Perception, 13(2), 209-246. https://doi.org/10.2307/40285694
- Stover, C. (2009). A theory of flexible rhythmic spaces for diasporic African music. Unpublished doctoral dissertation, University of Washington, USA.
- Washburne, C. (1998). Play it 'con filin'!: The swing and expression of salsa. Latin American Music Review, 19(2), 160-185. https://doi.org/10.2307/779989
- Wilson, O. (1974). The significance of the relationship between Afro-American music and West African music. The Black Perspective in Music, 2(1), 3-22. https://doi.org/10.2307/1214144
Appendix
The following transcriptions omit accent, pitch, pattern variants, and other important phrasing information. Their purpose is nothing more than to provide a basic reference for the analyses.